周期性边界条件下多孔肋片电磁热弹性力学性能分析

Analysis of Electromagnetic Thermoelastic Mechanical Properties of Porous Fins under Periodic Boundary Condition

摘要: 基于Lord-Shulman 广义热弹性理论，本文研究了一维实心肋片、多孔肋片在竖直方向的均匀磁场作用下受瞬态热冲击的电磁热弹性耦合问题，通过数值方法求解控制方程，得到了温度和应力分布规律。此外，还研究了在非傅立叶条件下，多孔肋片的孔隙效应(Np)、对流效应(Nc)和辐射效应(Nr)对温度和应力的影响。结果表明：在非傅立叶条件下，孔隙效应、辐射效应和对流效应有利于传热的进行，多孔肋片的传热效率随各参数的增大而增大，且与其他参数相比，辐射效应对温度和应力的影响最显著。

Abstract: Based on the Lord-Shulman generalized thermoelastic theory, this paper studies the electromag-netic thermoelastic coupling problem of one-dimensional solid fins and porous fins subjected to transient thermal shock under the action of a vertical uniform magnetic field. The control equation is solved by numerical method, and the distribution of temperature and stress is obtained. In addi-tion, the effects of the pore effect (Np), convection effect (Nc) and radiation effect (Nr) on the tem-perature and stress of the porous rib are also studied. The results show that the pore effect, radia-tion effect and convection effect are beneficial to heat transfer under non-Fourierheat condition. The heat transfer efficiency of porous fin increases with the increase of parameters, and the radia-tion effect has the most significant effect on temperature and stress compared with other parame-ters.

1. 引言

超集成化产品工作时，其表面会在短时间之内产生超高的温度或者热流，进而影响产品的性能和寿命，因此如何实现其表面的快速散热是近些年来学者们关注的焦点 [1] [2]。在换热表面加装肋片是实现强化换热的一种高效手段，这种方法在燃料电池热管理、蓄能、换热器等工业领域有着广泛的工程应用。它通过增大肋片换热面积以及破坏边界层增大传热系数，从而达到增强换热的目的，肋片的强化换热能力与其形状、材料以及几何参数等因素有关，因此，众多研究者不断地寻找能够使散热率最大化的肋片结构。与实心肋片相比，多孔肋片增加了单位体积下的热交换面积，而且通过去除空心孔的固体材料减轻了重量，是一种应用前景良好的换热方式。

Kraus等 [3] 对有关经典肋片的原理及设计作了较为全面的总结。Kiwan和AJ-Nimr [4] 率先提出了利用多孔肋片强化传热的概念，并通过与实心肋片对比，发现在相同条件下，多孔肋片的传热效率更高。Hoshyar [5] 分析了多孔介质肋片内热源随温度变化的的对流传热性能。Darvishi [6] 等使用频谱搭配方法对全湿多孔直肋片中自然对流和辐射换热进行了热分析。Gorla等 [7] 采用四阶龙格库塔方法研究了直肋片内辐射和自然对流耦合传热的问题，研究表明，与不考虑辐射影响的肋片相比，考虑了辐射影响的肋片散热效果更好。Hatami等 [8] 分析了不同几何截面的多孔介质陶瓷肋片散热情况。Atouei等 [9] 采用最小二乘法和配置法获得了热源和导热率均为温度函数的条件下的半球形肋片的温度分布。Nasser等 [10] 研究了非傅里叶条件下一维实心肋片的热弹性耦合问题，得到了肋片内温度及应力的分布规律。He等 [11] 研究了在非傅里叶条件下，均匀磁场作用的实心肋片受热冲击的电磁热弹性耦合问题，利用拉普拉斯数学求解得到了肋片的温度及应力分布规律。当肋片长期处于磁场、温度场等多场耦合的复杂环境下，肋片材料会由于非均匀温度场引起的热应力作用产生热疲劳，这是导致肋片发生断裂的重要因素。并且在非傅立叶条件下，肋片受瞬态热冲击所引起的热应力变化剧烈，因此分析多孔肋片在多场条件下的电磁热弹性问题对于肋片的设计和安全性具有重要的工程意义。

由Lord和Shulman发展起来的热弹性理论，通过在经典傅里叶热传导定律中引入热流密度及热松弛时间τ获得了一种新的波形热传导定律，确保了热波的有限传播速度。本文基于Lord-Shulman广义热弹性理论建立了肋片内的电磁热弹耦合方程，主要从两个方面进行研究。首先，以一维实心肋片为研究对象，着重分析肋片在瞬态热冲击下，磁场强度对肋片内应力及温度分布的影响。其次，研究了多孔肋片在非傅里叶条件下受瞬态热冲击的多场耦合问题，分析了多孔肋片的孔隙效应，对流效应及辐射效应对多孔肋片的温度及应力分布的影响。

2. 物理模型与数学模型

物理模型如图1所示，多孔肋片处于一个磁场强度为H₀方向竖直向上的磁场中。假设肋片在垂直纸面方向上不发生变化，并且肋片表面上的换热热阻远小于导热热阻，即任一截面上的温度是均匀的，因此将肋片受热冲击简化为一维问题 [12]。肋片顶端绝热，肋基受瞬态热冲击 ${\theta }_0={\theta }_{0}H\left(t\right)$，式中 ${\theta }_0$ 为热冲击的幅值，为一固定值，H(t)为Heaviside 阶跃函数。热冲击 ${\theta }_0={\theta }_{0}H\left(t\right)$ 表明，在时间无限小的情况下，肋片左端温度升到 ${\theta }_0$，并保持不变。计算中不考虑热在边界上的反射问题，并忽略环境中的湿度影响。流体与多孔介质之间的相互作用满足达西定律 [13]，肋片左右两端应力自由，均为零值。

Figure 1. Physical model

图1. 物理模型

描述传热过程的导热方程为：

$k\frac{{\partial }^{2}T}{\partial x^2}=\rho c_E\frac{\partial T}{\partial t}+\tau \rho c_E\frac{{\partial }^{2}T}{\partial t^2}+\gamma T_0\frac{{\partial }^{2}u}{\partial t\partial x}+\tau \gamma T_0\frac{{\partial }^{3}u}{\partial t^2\partial x}+S+\tau S^{\prime }$ (1)

式中， $\gamma =\left(3\lambda +2\mu \right){\alpha }_t$ , ${\alpha }_t$ 为线性膨胀系数。S项分别对应肋片的对流、辐射及孔隙率的影响 [14]：

$\begin{array}{c}S=\frac{hP\left(1-\phi \right)}{A}\left(T-T_0\right)+\frac{\epsilon \sigma F_{f\text{-}a}P\left(1-\phi \right)}{A}\left(T^4-T_0^4\right)+\phi \frac{{\rho }_f{c}_{E,f}�{\beta }_{f}KP}{{\nu }_{f}A}{\left(T-T_0\right)}^2\\ =\frac{h_{a}P\left(1-\phi \right)}{A}\frac{{\left(T-T_0\right)}^{m+1}}{{\left(T_b-T_0\right)}^m}+\frac{\epsilon \sigma F_{f\text{-}a}P\left(1-\phi \right)}{A}\left(T^4-T_0^4\right)+\phi \frac{{\rho }_f{c}_{E,f}�{\beta }_{f}KP}{{\nu }_{f}A}{\left(T-T_0\right)}^2\end{array}$ (2)

上式中，h为对流换热系数， $h=h_a\frac{{\left(T-T_0\right)}^m}{{\left(T_b-T_0\right)}^m}$，m表示不同的热传递模式。从导热方程中可以看出，温度场的分布受运动场的影响。

描述应变过程的运动方程为：

$\rho \frac{{\partial }^{2}u}{\partial t^2}=\left(\lambda +2\mu \right)\frac{{\partial }^{2}u}{\partial x^2}-\gamma \frac{\partial T}{\partial x}+{\mu }_e{H}_0^2\frac{{\partial }^{2}u}{\partial x^2}$ (3)

运动方程中， ${\mu }_e{H}_0^2\frac{{\partial }^{2}u}{\partial x^2}$ 表征磁场项，运行场的分布受到温度场和磁场的共同影响。

应力方程为：

$\sigma =\left(\lambda +2\mu \right)\frac{\partial u}{\partial x}-\gamma T+{\mu }_e{H}_0^2\frac{\partial u}{\partial x}$ (4)

上述各式中的物理量代表的含义如表1所示。

引入如下无量纲量：

$x^{\text{*}}=c_1{\eta }_{1}x$， $u^{\text{*}}=c_1{\eta }_{1}u$， $t^{\text{*}}=c_1^2{\eta }_{1}t$， ${\tau }^{\text{*}}=c_1^2{\eta }_1\tau$， ${\theta }^{*}=T/T_0$， ${\sigma }^{\text{*}}=\sigma /\mu$，

$b=\frac{\gamma T_0}{\mu }$， $g=\frac{\gamma }{\rho c_E}$， $h=\frac{{\mu }_e{H}_0^2}{\mu }$， ${\beta }^2=\frac{\lambda +2\mu }{\mu }$， $ϵ=\frac{{\mu }_e{H}_0^2}{\mu }$，

$N_c=\frac{k}{{\left(\rho c_E{c}_1\right)}^2}\frac{h_{a}P\left(1-\phi \right)}{A{\left({\theta }_b-{\theta }_0\right)}^m}$， $N_r=\frac{k\epsilon \sigma F_{f\text{-}a}P\left(1-\phi \right)}{{\left(\rho c_E{c}_1\right)}^{2}A}{T}_0^3$， $N_p=\frac{k}{{\left(\rho c_E{c}_1\right)}^2}\phi \frac{{\rho }_f{c}_{E,f}�{\beta }_{f}K{T}_{0}P}{{\nu }_{f}A}$。其中，c₁为等温弹性波的传播速度， $c_1^2=\frac{\lambda +2\mu }{\rho }$， ${\eta }_1=\frac{\rho c_E}{k}$。

对方程(1) (3) (4)进行无量纲处理：

$\frac{{\partial }^2\theta }{\partial x^2}=\left(1+\tau \frac{\partial }{\partial t}\right)\left(\frac{\partial \theta }{\partial t}+g\frac{{\partial }^{2}u}{\partial t\partial x}+N_c{\left(\theta -{\theta }_0\right)}^{m+1}+N_r\left({\theta }^4-{\theta }_0^4\right)+N_p{\left(\theta -{\theta }_0\right)}^2\right)$ (5)

${\beta }^2\frac{{\partial }^{2}u}{\partial t^2}=\left({\beta }^2+ϵ\right)\frac{{\partial }^{2}u}{\partial x^2}-b\frac{\partial \theta }{\partial x}$ (6)

$\sigma =\left({\beta }^2+ϵ\right)\frac{\partial u}{\partial x}-b\theta$ (7)

初始条件：

$\theta \left(x,t\right)=0,t=0$

$u\left(x,t\right)=0,t=0$

边界条件：

$\theta \left(x,t\right)={\theta }_{0}H\left(t\right),x=0$

$\sigma \left(x,t\right)=0,x=0$

$\frac{\partial \theta }{\partial x}=0,x=L$

$\sigma \left(x,t\right)=0,x=L$

Table 1. Symbol table

表1. 名词符号表

3. 验证

本文采用数值离散方法对该问题进行求解。为验证程序的可靠性，利用该程序计算了不同时刻自由状态下实心铜肋片内的温度和热应力分布情况，并与拉普拉斯变换的数值反演 [10] 进行了对比，其结果如图2所示。相关参数如下：

$\lambda =\text{7}.\text{76}$， $\mu =3.86\times {10}^{10}$， ${\alpha }_t=1.78\times {10}^{-5}$， $С=383.1$， $\rho =8954$， $T_0=293$，

$\epsilon =0.161$， ${\beta }_2=4$， $b=0.042$， $g=1.61$， ${\theta }_0=1$， $L_x=1$， $\tau =0.02$

可以发现，数值计算结果与解析解基本一致。因此，编写的程序是可靠的。

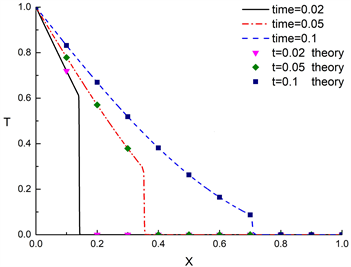(a) 温度分布 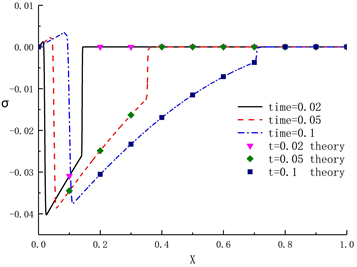(b) 应力分布

Figure 2. Model validation

图2. 模型验证

4. 结果与讨论

4.1. 磁场强度对实心肋片温度和热应力的影响

固体在热冲击下会发生变形从而产生应力，由于磁场的作用，肋片内的温度及应力分布均会受到影响。论文研究了在磁感强度恒定的电磁场作用下，实心肋片在其表面受热冲击时的电磁热弹性耦合问题。肋片材料为铜，相关参数同上，磁感强度H₀ = 5 × 10⁸，热松弛时间τ= 0.02，θ₀ = 1，L_x = 1。

无量纲时间分别为0.05、0.1时不同磁场强度下的温度及应力响应如图3所示。从图中可以看到，在同样的无量纲时间下，磁场强度对温度分布的影响甚微，其影响主要体现在应力上。如图3(b)所示，靠近肋基的部分由于受到热冲击膨胀而产生拉应力，沿X轴方向向后介质产生压应力，发生压缩变形，热波没有传递到的部分则保持零值。变形是一个动态过程，随着时间的推移，膨胀区逐渐向后移动，并且数值变大。其次，同样的无量纲时间下，磁场强度会对应力场分布有影响。若物理模型加入磁场项，得到的应力分布拉压应力拐点会向后偏移，但是并不影响热波跳跃不连续的位置，会在同一时刻跳跃到零值。相对于无磁场的情况，磁场的存在会使拉应力与压应力增大，应力波的传播速度加快波动更剧烈，对实际的工程项目有重要指导意义。

(a) 电磁力对温度的影响 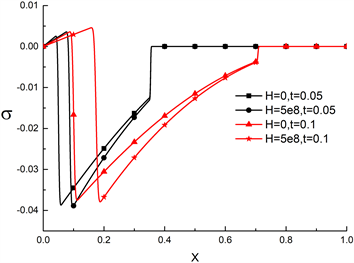(b) 电磁力对应力的影响

Figure 3. Influence of electromagnetic force on temperature and stress

图3. 电磁力对温度和应力的影响

4.2. 孔隙率对多孔肋片内温度和热应力的影响

论文进而考虑了多孔肋片孔隙率、对流效应及辐射效应对肋片性能的影响，研究了一维多孔肋片在其表面受热冲击时的电磁热弹性耦合问题。引入孔隙参数φ，肋片材料取铜，参数同上，取H₀ = 0，热松弛时间τ = 0.02，θ₀ = 1，L_x = 1。

图4显示了在傅里叶和非傅里叶条件下，温度和应力分布随孔隙参数(N_p)的变化，忽略辐射和对流效应(N_c = 0, N_r = 0)。当不考虑非傅里叶效应，即无量纲弛豫时间为0 (τ = 0)时，温度及应力分布不存在间断性，这可以解释为热波以无限的速度传播。

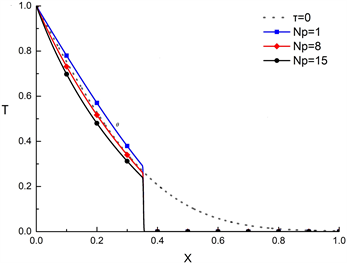(a) 温度分布 (b) 应力分布

Figure 4. Temperature and stress distribution (N_r = 0, N_c = 0, t = 0.05)

图4. 温度和应力分布(N_r = 0, N_c = 0, t = 0.05)

当考虑非傅里叶效应时，图4(a)为无量纲时间0.05时多孔肋片的温度分布图，从图中可看出，不连续性发生在X = 0.35，即热扰动只传递到X < 0.35区域。另外，无量纲温度随N_p的增加而降低，这是因为N_p值越高，多孔肋片的温度梯度越大，传热速率越快，所以随着N_p的增加，肋片接近周围温度的速度更快。此外，尽管N_p值的变化会影响温度分布，但是并不影响跳跃不连续的位置。图4(b)显示了热应力随不同孔隙率参数N_p的分布情况。同温度分布一样，不连续性发生X = 0.35。另外，N_p值对拉压应力区域的影响不一致，在靠近肋基侧拉应力区域，随着N_p参数的增加，拉应力逐渐增大；在压应力区域，应力值随N_p参数的增大而减小。并且，N_p值的变化并不影响拉压应力拐点和热波不连续的位置。

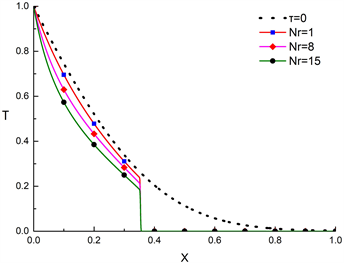
图5描述了辐射换热效应N_r对肋片内温度和应力分布的影响(N_c = 0，N_p = 8，N_r = 1、8、15)。图6显示的是不同N_c值对肋片换热的影响(N_p = 8，N_r = 1，N_c = 1、5、10)。根据图4、图5、图6可以得到，N_p，N_r，N_c对肋片散热和应力均具有积极影响，增大各个参数值可以使肋片散热更快，同时降低热应力。与其他参数相比，N_c对肋片传热及应力的影响最小，N_r影响最大。

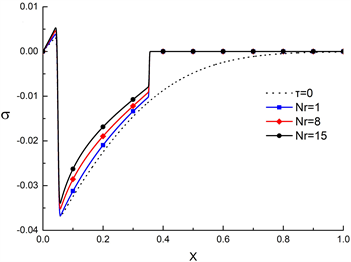(a) 温度分布 (b) 应力分布

Figure 5. Temperature and stress distribution (N_p = 8, N_c = 0, t = 0.05)

图5. 温度和应力分布(N_p = 8, N_c = 0, t = 0.05)

(a) 温度分布 (b) 应力分布

Figure 6. Temperature and stress distribution (N_p = 8, N_r = 1, t = 0.05)

图6. 温度和应力分布(N_p = 8, N_r = 1, t = 0.05)

4.3. 周期性边界条件对多孔肋片内温度和热应力的影响

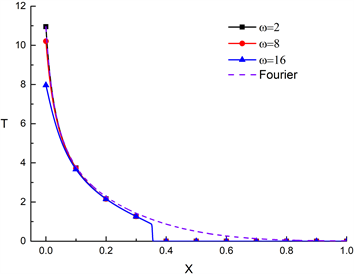
本节研究了多孔肋片在周期性边界条件热冲击下的电磁热弹耦合问题。肋基温度为 $\theta ={\theta }_0+B\cos \left(wt\right)$，取θ₀ = 1，B = 10，w = 2、8、16。图7(a)描述了傅里叶和非傅里叶条件下不同频率值对肋片温度分布的影响，从图中可以得知，频率的变化没有影响到温度的不连续性。图7(b)热应力分布中，增加w值会导致靠近肋基的膨胀区域拉应力变大，压缩区域压应力减小，同时w值的改变不会影响拉压应力拐点和波动不连续的位置。值得一提的是，在材料物性参数及热松弛时间确定的情况下，只有无量纲时间会影响热波的传播距离，其余参数均无影响。

(a) 温度分布 (b) 应力分布

Figure 7. Temperature and stress distribution (N_p = 8, N_r = 1, t = 0.05)

图7. 温度和应力分布(N_p = 8, N_r = 1, t = 0.05)

5. 结论

本文研究了多孔肋片处于电磁空间受瞬态热冲击时的电磁热弹性耦合问题。首先以实心肋片为研究对象，分析了磁场强度对肋片内温度及应力分布的影响，进而研究了孔隙率效应N_p、辐射效应N_r、对流换热效应N_c对多孔肋片换热性能的影响。结果表明：1) 当肋片处于磁场环境下，磁场强度对温度分布影响很小，主要影响应力分布。磁场强度的存在会导致应力分布拉压应力拐点会向后偏移，但是热波跳跃不连续的位置不会改变。2) N_p，N_r，N_c能增大肋片换热效率，其中N_r对传热的影响最大，N_c影响最小。3) 无量纲温度及热应力分布间断的位置受弛豫时间和无量纲时间的影响，而N_p，N_r，N_c等参数对温度间断没有影响。

NOTES

^*通讯作者。