基于新冠肺炎疫情下的防控策略优化

Optimization of Prevention and Control Strategies Based on the COVID-19

摘要: 2019年突如其来的新冠肺炎疫情(COVID-19)席卷全球，利用Matlab建立SEIR模型、二次指数平滑模型对部分典型国家的确诊病例数量、国内生产总值(GDP)进行预测，考虑对待新冠肺炎疫情的防控策略，采用模糊评价模型对新增确诊人数进行预测与分析。

Abstract: In 2019, the sudden new crown pneumonia epidemic (COVID-19) swept the world. This paper uses Matlab to establish an SEIR model and a quadratic exponential smoothing model to predict the number of confirmed cases and gross domestic product (GDP) in some typical countries, and con-siders the prevention and control strategy of the COVID-19 epidemic. The fuzzy evaluation model is used to forecast and analyze the number of newly confirmed cases.

1. 引言

本文源于2020年湖南省高校第五届研究生数学建模竞赛A题 [1] 。2019年底，湖北省武汉市发现不明原因肺炎病例，中国在第一时间采取措施，开展病因和流行学调查。经研究发现，此肺炎是由新型冠状病毒引起的，该新型冠状病毒(COVID-19)传染性极强 [2] ，且有1~14天的潜伏期，管控难度极大。在很短的时间内席卷全球。2019年12月出现新冠疫情后，全球确诊人数急剧上升，截止至2020年11月，国内累计确诊人数已达9万多人，国外累计确诊人数已达6100多万人 [3] 。我国在采取强有力的管控措施和民众的积极配合下，疫情得到有效控制，目前仅有1000余例病例；而海外疫情仍处在上升阶段，现有确诊依然高达1768万余例。在疫情的影响下，全球价值链(GVC)受到巨大冲击 [4] ，GVC是21世纪国际生产体系最显著的特征，它使得世界各国通过贸易互联互通。新冠疫情直接冲击了全世界的实体经济，由于新冠病毒极强的传染性，导致GVC体系内的各元素相互影响。进一步对全球贸易、资本市场等经济层面产生巨大破坏 [5] 。因此应该采取高效的防疫方案尽快抑制疫情的传播，才能实现经济增长，恢复全球经济市场的活力 [6] 。针对确诊病例的预测模型，选取三个典型国家，建立SEIR模型进行预判分析，再结合微分方程根据下一代矩阵方法基本再生数R。通过财经网站收集典型国家的GDP数据，为了简化模型，采取了二次平滑模型进行2021年的GDP预测。对于新增确诊病例预测模型，建立了综合评价模型对典型国家的分析评价，在此基础之上利用曲线拟合模型对典型国家的新增病例进行预测。

2. 确诊病例的预测模型

2.1. 数据来源

获取自2020年1月24日至2020年11月27日来源于世界卫生组织的新冠肺炎疫情相关数据，以及各阶段(如图1所示)来自中国国际贸易促进委员会关于有关国家(地区)因新冠肺炎疫情采取的相关措施的数据，并进行进一步处理。各国采取主要措施有：

1) 对货物贸易(除医疗物资外)采取措施；

2) 对医疗物资贸易采取措施；

3) 对船舶、航班、列车采取措施；

4) 对边境口岸采取措施；

5) 对人员入境采取措施；

6) 宣布进入紧急状态的国家(地区)。

假设在相对理想的环境的下，通过对采取措施的各个阶段的新冠肺炎确诊人数以及各国现存确诊病例的人数进行研究，确定封闭型、半封闭型、非封闭型这三种疫情现状的三个典型国家。

封闭型：中国；

半封闭型：韩国；

非封闭型：美国。

Figure 1. As of November 27, 2020, the top ten countries (or regions) with existing confirmed cases of new crown pneumonia

图1. 截止2020年11月27日新冠肺炎疫情现存确诊前十个国家(或地区)

2.2. 模型建立与分析

采取基于SEIR模型 [7] 来对中国、美国、韩国的确诊病例数量进行预测分析。SEIR模型与实际情况密切贴合，对所提出的问题结合实际情况进行求解，求解结果更具有效性和权威性；基于SEIR的模型算法新颖，计算过程简单，简化了问题求解过程。

$\{\begin{array}{l}\frac{\text{d}S}{\text{d}t}=-\beta \left(I+\theta A\right)-pS+\lambda Q,\\ \frac{\text{d}Q}{\text{d}t}=pS-\lambda Q,\\ \frac{\text{d}E}{\text{d}t}=\beta \left(I+\theta A\right)-\sigma E,\\ \frac{\text{d}A}{\text{d}t}=\sigma \left(1-\rho \right)E-{\epsilon }_{A}A-{\gamma }_{A}A,\\ \frac{\text{d}I}{\text{d}t}=\sigma \rho E-{\gamma }_{I}I-d_{I}I-{\epsilon }_{I}I,\\ \frac{\text{d}D}{\text{d}t}={\epsilon }_{A}A+{\epsilon }_{I}I-d_{D}D-{\gamma }_{D}D,\\ \frac{\text{d}D}{\text{d}t}={\epsilon }_{A}A+{\epsilon }_{I}I+{\gamma }_{D}D.\end{array}$ (1)

对SEIR模型进行求解，确定其对应参数即可求出相应结果：

1) S(t)——易感人群数量；

2) Q(t)——隔离人群数量；

3) E(t)——暴露人群数量；

4) A(t)——无症状感染人群数量；

5) I(t)——有症状感染人群数量；

6) D(t)——确诊人群数量；

7) R(t)——康复人群数量；

8) $\beta$ ——接触率；

9) $\rho$ ——隔离人群的隔离率；

10) $\lambda$ ——隔离人群的释放率；

11) $\sigma$ ——暴露人群转换为感染人群的转换率；

12) $\epsilon$ ——诊断率；

13) $1/\gamma$ ——人群康复率；

14) 1/d——人群死亡率。

Figure 2. Matlab simulation map

图2. Matlab仿真图

通过Matlab仿真，仿真结果和数据结果大致相同(见图2)，以中国为例，传染人群和潜伏人群在前期都成上升趋势，但是增长较为缓慢。通过采取一系列防控措施之后，传染人群达到高峰后开始下降并逐渐消失，仿真结果和数据结果大致相同。

将采取的不同的防疫措施分为主要三类，人口免疫、医疗隔离、居家隔离，这三种主要措施相对应的是移除率对疫情的影响、感染人群的隔离率对疫情的影响以及无症状感染人群的隔离对疫情的影响，同时也分别对应了上述国家不同的防疫措施对疫情的影响。

为了验证各种防疫措施对疫情传播的影响的有效性，我们采取文献 [8] 中结合微分方程根据下一代矩阵方法计算基本再生数R：

$R=\left(1+{}_{r}T{}_L\right)\cdot \left(1+{}_{r}T{}_I\right)$ (2)

其中r表示指数增长的增长率，如果用b(t)表示第t天的新增感染人数，则：

$b\left(t\right)=b\left(t-\Delta t\right){\text{e}}^{r\Delta t}$ (3)

T_L和T_I都是来自对现实情况的观察，T_L表示被感染者的潜伏期的平均长度， $T_L=S_I-T_I$ 、S_I的定义分别为一个零感染者被感染的时间和他的下一个人被感染的时间的间隔。跟据参考文献 [9] 中，得到S_I和T_L分别为14天和7天。

通过计算基本再生数R，来分析评价上述三类国家的疫情防控质量效果。关于基本再生数R，他所表示的是一种病例在一个全是易感人群中造成新的感染者的平均人数。当R < 1时，即感染人群在平均感染期内能造成的感染人数小于1，此时这个疾病会逐渐消亡。反之，该地区的疾病传播程度更加严重。我们通过对上述国家的三个阶段的数据进行统计，得到其基本再生数R (见表1)，以此来评价各个国家采取的不同措施对疫情的影响。

Table 1. Average value of basic reproduction number R

表1. 基本再生数R的平均值

根据基本再生数R的情况我们得知，封闭型国家代表中国，在采取医学隔离和居家隔离等措施后，疫情情况在到达高峰期后逐渐下滑，R值达到1以下，符合疫情实际情况。半封闭型国家代表韩国，在采取部分医学隔离等措施后，但是并未采取封闭措施，疫情情况先减少后，因为境外输入，感染人数又进一步增加。非封闭国家代表美国，因没有采取一些防疫措施，疫情持续增长，与统计结果相符。

3. 疫情之下的经济预测趋势

3.1. 指数平滑模型

考虑到一次指数平滑法虽然克服了移动平均法的缺点，但当时间序列的变动出现直线趋势时，用一次指数平滑法进行预测，仍存在明显的滞后偏差，因此，也必须加以修正，再作二次指数平滑，利用滞后偏差的规律建立直线趋势模型，指数平滑预测模型对不同时间的数据的非等权处理比较符合实际情况；预测模型能自动识别采集数据的变化而调整，这就是二次指数平滑法 [10] 。所以为了考虑更加全面的因素，此处使用二次平滑指数法，其计算公式为：

$\{\begin{array}{l}{S}_t^{\left(1\right)}=\alpha y_t+\left(1-\alpha \right)S_{t-1}^{\left(1\right)}\\ S_t^{\left(2\right)}=\alpha S_t^{\left(1\right)}+\left(1-\alpha \right)S_{t-1}^{\left(2\right)}\end{array}$ (4)

其中： $S_t^{\left(1\right)}$ 为一次指数的平滑值； $S_t^{\left(2\right)}$ 为二次指数的平滑值。当时间序列{y_t}从某时期开始具有直线趋势时。可用直线趋势模型：

${\hat{y}}_{t+m}=a_t+b_{t}m,m=1,2,\cdot \cdot \cdot ,$ (5)

$\{\begin{array}{l}{a}_t=2S_t^{\left(1\right)}-S_t^{\left(2\right)},\\ b_t=\frac{\alpha }{1-\alpha }\left(S_t^{\left(1\right)}-S_t^{\left(2\right)}\right),\end{array}$ (6)

进行预测。

3.2. 解题过程

收集中美韩三国近十年以来的GDP总值，建立二次平滑指数模型对其进行GDP的预测：得到2021年中、韩、美的GDP预测值分别为14.40、1.52、20.48万亿美元。

Figure 3. Chinese GDP compared with the predicted values

图3. 中国GDP与GDP预测值比较

由图3可看出，我国预测GDP总值呈持续增长趋势，实际GDP总值围绕预测值有小幅度波动，但基本上与预测值相吻合。还可以发现，在2020年间，实际总值呈大幅下降趋势，对于这个现象的解释可以主要归因于疫情的影响。疫情对国内经济市场以及对外贸易、全球经济链造成重大冲击，尤其是直接冲击了实体业，破坏了我国的生产结构和贸易壁垒，滞后了经济发展，导致实际总值下降。此外可以发现，在2008年我国经历地震、冰灾等大型自然灾害后实际总值反而呈上升趋势，可以预测疫情过后我国的GDP总值会有上升，甚至可能超过之前的预测数值。

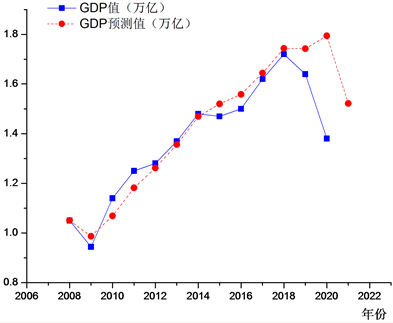
Figure 4. Korean GDP compared with the predicted values

图4. 韩国GDP与GDP预测值比较

从这十年的GDP实际情况和预测情况(见图4)，韩国在这十年的GDP值在预测GDP曲线上下波动，2017年韩国大选对韩国的经济造成下滑趋势，2019年底突发新冠疫情，前期由于我国的有效管控，春节赶赴韩国的我国游客数量大幅下降，旅游、航空、酒店等行业受到冲击，但随着韩国国内的疫情加剧，韩国的外贸进出口产业受到重大冲击，韩国作为一个严重的依赖海外贸易的国家，此次疫情冲击导致韩国的经济严重下滑。资本市场惨淡，融投资形势不容乐观，金融和资本不会得病，然而疫情的影响，让投资者的信心大受影响。目前疫情已经基本波及全球主要发达和新兴经济体，韩国企业本身投资计划基本被打破，任何区域的实体经济产业都会受疫情波及。韩国本土目前的疫情和经济状况，也让境外投资者望而却步，韩国企业从境外获得融资可能性大大降低。所以韩国的GDP在今年与预测GDP出现了较大的落差。

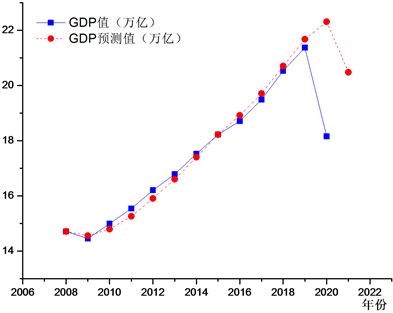
Figure 5. American GDP compared with the predicted values

图5. 美国GDP与GDP预测值比较

由图5可以看出美国的国内生产总值从2008年到2009年保持稳定，2009年之后保持着持续上升。美国的GDP和美国的预测GDP都是保持着差不蛮多的曲线，直到2020年新冠疫情的爆发美国GDP发生了变化，没有向预测GDP的方向发展，由此可以看出新冠疫情对美国经济的冲击是比较大的。美国经济短期内的衰退似乎已难以避免，尽管美国经济可能已经陷入衰退，但疫情本身并未破坏美国经济良好的发展基础，现在的政策是为了保证疫情过后经济可以强劲复苏。在疫情的压力下，美国经济的许多痼疾存在集中爆发的可能，美国中长期经济增长的形势并不乐观。

3.3. 模型分析

自今年新冠疫情爆发以来，我国采取了积极及时的抗疫措施，武汉封城，全国积极响应，前赴后继的医务工作者逆行支援，疫情得到了基本的控制。尽管美国在经济发展水平和医疗设施等方面都领先于中国，但是新冠疫情在美国却造成了更大的负面影响。相比于我们举国协力的努力带来的短暂阵痛，美国由于其政治制度及社会环境的制约，经历了更长时间和更大程度的损伤。到11月28日为止，美国的累计确诊数量已经达到了13,610,357人，死亡人数也达到了272,254人。韩国的这种半封闭状态相比封闭而言，效果略有成效，与中国这种全封闭的国家相比，却有严重的不足，但由于与经济全球化的联系密不可分，与中国相比，韩国这种经济体制在全球突发公共卫生事件的影响之下无法自给自足，对疫情后经济的恢复有很大难度，也由此可以提现中国特色社会主义的优越性。

但在疫情的冲击和严格的抗疫措施下，我国的经济社会发展不可避免的受到了巨大的影响。根据图表里中国国内国内生产总值与预测的GDP值走向来看，2020年新冠肺炎疫情对我国GDP近些年来的持续稳定发展造成了较大影响，但总体来说，也还没有达到太令人消极的地步。为了刺激经济的复苏，政府部门出台了多条政策措施支持复工复产，国家加强了对宏观经济的调控，货币供应量增加，贷款利率下降，我国的经济开始慢慢复苏，金融市场形势见好。为使新冠疫情的影响与发展能被更加全面的认识，本文将从多个角度进行分析，并通过时间序列预测疫情影响时间。

疫情虽然会对中国经济发展和经济增长带来深刻挑战，但是并不会改变中国经济长期向好的根本趋势。疫情的发生，从某种意义上进一步提示我们，要加快转变发展方式，推动全面改革、全面治理，解放和发展生产力，推进国家治理体系和治理能力现代化。

4. 新增确诊病例的预测模型

4.1. 建立模型

采用一级模糊综合评判模型 [11] 来预测新增确诊病例数，一级模糊综合评判模型的建立，主要包括以下步骤：

确定因素集。对员工的表现，需要从多个方面进行综合评判，如员工的工作业绩、工作态度、沟通能力、政治表现等。所有这些因素构成了评价指标体系集合，即因素集，记为：

$U=\{u_1,u_2,u_3,\cdots ,u_n\}.$ (7)

确定评语集。由于每个指标的评价值不同，往往会形成不同的等级。如对工作业绩的评价有好、较好、中等、较差、很差等。由各种不同决断构成的集合称为评价集，记为：

$V={\{v}_1,v_2,\cdots ,v_m\}.$ (8)

确定各因素的权重。一般情况下，因素集中的各因素在综合评价中所起的作用是不相同的，综合评价结果不仅与各因素的评价有关，而且在很大程度上还依赖于各因素对综合评价所起的作用，这就需要确定一个各因素之间的权重分配，它是U上的一个模糊向量，记为：

$A=[a_1,a_2,\cdots ,a_n].$ (9)

其中： $a_i$ 表示第i个因素的权重，且满足 ${\displaystyle \underset{i=1}{\overset{n}{\sum }}{a}_i}=1$ ，确定权重的方法很多，如Delph法、m权平均法、众人评估法等。

确定模糊综合判断矩阵。对指标 $u_i$ 来说，对各个评语的隶属度为V上的模糊子集。对指标u的评判记为：

$R_i=[r_{i1},r_{i2},\cdots ,r_{in}].$ (10)

各指标的模糊综合判断矩阵为

$R=\left[\begin{array}{cccc}{r}_{11}& r_{12}& \cdots & r_{1m}\\ r_{21}& r_{22}& \cdots & r_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ r_{n1}& r_{n2}& \cdots & r_{nm}\end{array}\right],$ (11)

它是一个从U到V的模糊关系矩阵。

综合评判。如果有一个从U到V的模糊关系 $R={\left(r_{ij}\right)}_{n\times m}$ ，那么利用R就可以得到一个模糊变换 $T_R:F\left(U\right)\to F\left(V\right)$ 。由此变换，就可得到一个综合评判结果 $B=A\cdot R$ ，记为 $B=\left[b_1,b_2,\cdots ,b_m\right]$ 。预测在此防控方案下的各国2021年疫情变化趋势并采用最小二乘法曲线拟合模型 [12] 。最小二乘法可通过用最小化误差平方和来找到数据的最佳函数匹配。

由以上模糊综合评测体系，得出防控类型为完全封闭的中国，在评测结果上为“优秀”，半封闭的韩国，评测结果为“良好”，开放的美国，评测结果为“差”，可见中国在的这种防控方式对世界防疫效果最佳，在防疫实情下，绝对不可像美国一样，放任疫情不管理，国家还支持自由。韩国做法较为适中，也在一定程度上减缓了疫情的爆发。最终可以得出防控疫情的最优方案为完全封闭类型。

4.2. 数据分析

从图6右可知，预计2021年韩国的日增趋势会表现出先缓慢增加，然后以指数型增长的趋势，即疫情得不到控制。

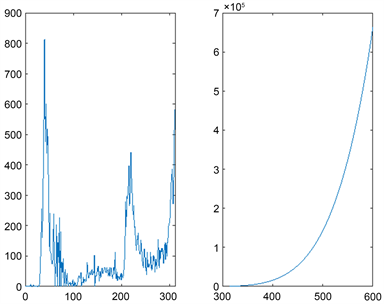
Figure 6. The Matlab forecast analysis chart of the trend of newly diagnosed people in Korea

图6. 韩国新增确诊人数趋势MATLAB预测分析图

从图7右可得出，预测2021年美国日增趋势同样是呈指数型增长，疫情会在美国土地上肆意疯涨。

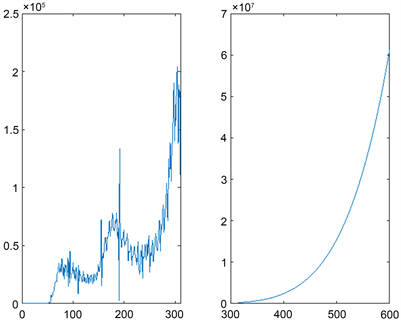
Figure 7. The Matlab forecast analysis chart of the trend of newly diagnosed people in American

图7. 美国新增确诊人数趋势MATLAB预测分析图

从图8右得出结论，在对2020年数据的分析处理后，预测出2021年日增确诊人数完全呈负增长，即不会再出现新增病例，疫情得到完全控制。

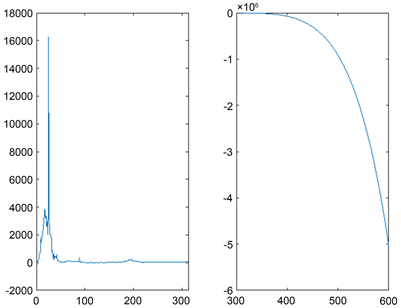
Figure 8. The Matlab forecast analysis chart of the trend of newly diagnosed people in China

图8. 中国新增确诊人数趋势MATLAB预测分析图

5. 结语

利用SEIR模型、指数平滑模型以及模糊评价模型对COVID-19确诊病例数量以及经济趋势(GDP)的预判，得出了在疫情之下，国家需要进行全封闭管控，防控不容忽视，预测结果和实际表明：我国的疫情防控是有效的，同时也体现了社会主义制度的优越性。

致谢

感谢湖南人文科技学院数学与金融学院对本文的支持。

基金项目

湖南省学位与研究生教育改革研究项目“专业学位硕士研究生创新人才培养的数学建模‘两轮驱动’模式研究与实践”(湘教通[2019]293号No.2019YGYB67)。

NOTES

^*通讯作者。