1. 引言
自发现Fe73.5Cu1Nb3Si13.5B9合金 [1] 材料以来,由于其具有优异的软磁性能而引起人们的广泛关注和深入研究 [2] [3] [4]。研究表明,应力退火 [5] [6] 感生的磁各向异性大于磁场退火 [7] [8] 所感生的磁各向异性,它的机理研究对优化材料磁性能具有重要的现实指导价值,但目前人们对应力感生磁各向异性机理的认识还存在诸多争议,Herzer等人 [9] 提出了磁弹耦合相互作用模型,Hofmann等 [10] 提出了基于neel原子对方向有序模型,之后Ohnuma等 [11] [12] [13] 通过透射X射线衍射技术直接观测到了应力退火引起了Fe基合金的晶格各向异性,主张晶格各向异性是感生磁各向异性的直接原因,表示应力感生磁各向异性与外加应力呈线性关系,并认为长时间或者多次回火可以消除感生的磁各向异性。但这些理论都未考虑到退火过程中非晶基底蠕变所产生的效应。方允樟等 [14] [15] 采用原子力显微镜对Fe基合金带横断面介观结构进行观测,提出了α-Fe(Si)纳米晶粒的定向团聚也是导致应力退火感生磁各向异性的重要原因。近期许校嘉等 [16] 通过多次回火实验表明应力退火感生的磁各向异性无法完全被消除,提出在Ohnuma等理论的基础上,还应该考虑方允樟等提出的颗粒定向团聚模型。本文主要采用同步辐射X射线衍射原位观测了Fe基纳米晶合金薄带微观应变,采用退火过程原位监测计算了样品的宏观应变,采用HP4294A型阻抗分析仪测定了样品磁各向异性,并计算退火后样品中纳米晶间的距离,探讨了应力对于纳米晶粒间的交换耦合作用的影响,提出了应力退火使纳米晶间隙改变,横向交换耦合作用增强,纵向减弱,从而产生的纳米晶分布各向异性是除晶格各向异性外,另一导致磁各向异性增大的重要因素。以期对应力感生磁各向异性机理的研究提供一定的帮助。
2. 实验
本文所使用的Fe基合金薄带(Fe73.5Cu1Nb3Si13.5 B9)是通过单辊快淬法制备得到的宽度为1 mm,厚度为35 μm的非晶薄带,分别对非晶薄带进行540℃ 0 MPa~410 MPa退火处理得到自由退火样品和应力退火样品,升温速率均为36℃/min,退火时间为30 min,整个退火过程附加流通氮气保护。利用Supereyes B011 5MP 500X数字摄像显微镜以及Supereyes软件,观测并记录样品的纵向宏观变化量。采用上海同步辐射装置(SSRF)的BL14W硬X射线对待测样品进行显微结构的表征。其中X射线的波长λ = 0.069 nm、能量E = 18.0 keV、分辨率为2.5 × 10−4。采用HP4294A型阻抗分析仪纵向驱动模式测量Fe基合金薄带的巨磁阻抗(GMI)曲线,并通过GMI曲线计算样品的磁各向异性。
巨磁阻抗比的计算公式表示为:
(1)
其中
为外加任意磁场Hex下样品对应的阻抗值,
为在外加最大磁场Hmax时样品对应的阻抗值,ΔZ/Z为巨磁阻抗比值。
样品的横向磁各向异性场计算公式表示为:
(2)
其中H+为样品样品GMI曲线半高宽处对应的正向磁场强度,H−为样品GMI曲线半高宽处对应的反向磁场强度,Hk为样品的横向磁各向异性场。
3. 结果与讨论
3.1. 不同退火样品的巨磁阻抗与磁各向异性
图1所示为不同应力(0 MPa~410 MPa)进行540℃退火后的样品,在400 kHz驱动频率下测得的巨磁阻抗比值随外加磁场的变化关系图。从图中可以看出,样品在540℃ 0MPa退火即自由退火的条件下,样品的GMI曲线呈现出一个窄高的尖锐峰,说明其对微弱的外磁场变化是敏感的。随着外加应力的增加,样品的峰的高度逐渐降低,宽度增大。当应力大于53 MPa,样品的GMI曲线开始出现了“平台”,说明样品对于该“平台”范围的外磁场敏感度减弱,并随着应力的逐渐增大,样品对于外磁场的不敏感区逐渐扩大。
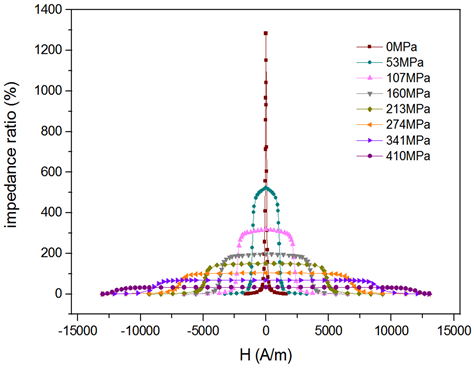
Figure 1. GMI curves of samples annealed at 540˚C under different stresses
图1. 540℃不同应力退火样品的GMI曲线
图2为应力退火样品的最大巨磁阻抗比(∆Z/Z)max、磁各向异性场Hk与应力σ之间的变化关系,样品在分别通过540℃ 0 MPa、53 MPa、107 MPa、160 MPa、213 MPa、274 MPa、341 MPa、410 MPa应力退火后,得到的最大巨磁阻抗比分别为1284.02%、523.46%、319.91%、197.78%、151.53%、104.22%、69.01%、38.99%,磁各向异性场分别为40.13 A/m、1055.51 A/m、2263.79 A/m、3604.76 A/m、4852.98 A/m、6868.76 A/m、8956.87 A/m、11969.39 A/m,通过对数据点进行处理得到拟合的曲线,可以发现样品的最大巨磁阻抗比(∆Z/Z)max随着外加应力σ的增加而减小,关系如式(3),样品感生的磁各向异性场Hk随着外加应力σ的增大呈指数增长,并非线性关系,关系如式(4)。
(3)
(4)
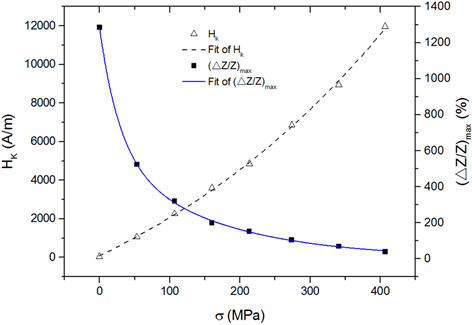
Figure 2. The relationship between the maximum giant magneto-impedance ratio, magnetic anisotropy field and stress of the sample
图2. 样品的最大巨磁阻抗比、磁各向异性场与应力的关系曲线图
3.2. 不同应力退火样品的微观结构
样品在进行540℃退火后内部已经产生了晶化,生成的是α-Fe(Si)纳米晶,由于XRD曲线中的(110)峰是非晶峰和晶化峰的叠加,会对实验结果造成一定的影响,所以为了排除非晶峰的影响,选取样品晶化后才出现的(200)峰进行处理,并计算样品的微观应变。图3表示0 MPa、107 MPa、160 MPa、213 MPa、274 MPa、410 MPa应力退火后样品在垂直和平行应力方向(200)峰位的变化,对比发现相对于自由退火样品,应力退火样品随着应力的增加(200)峰平行应力方向逐渐向着低角度偏移,垂直应力方向向着高角度偏移,从峰位的相对偏移可以看出,施加应力会使纳米晶垂直应力方向上的晶面间距减小,平行应力方向的晶面间距增大,从而产生纳米晶晶格各向异性。说明外加应力退火会使得样品晶化时产生纳米晶晶格各向异性,随着施加的张应力的增大,纳米晶的晶格各向异性也会随之增大。
3.3. 样品的宏观应变与微观应变
采用XRD曲线的(200)峰计算样品的微观应变,公式为:
(5)
其中
为样品中平行于应力方向的纳米晶的晶面间距,
为样品中垂直于应力方向的纳米晶的晶面间距,
为自由退火样品中纳米晶的晶面间距,
为样品的微观应变。
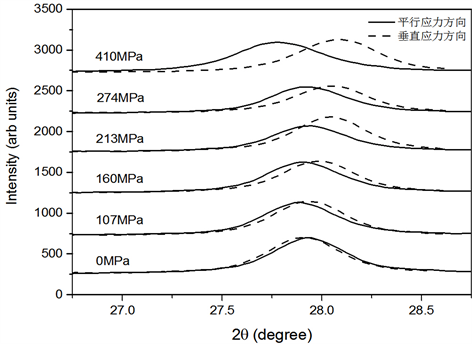
Figure 3. (200) peak position changes of free annealing and stress annealing samples in different directions
图3. 不同应力退火样品垂直和平行应力方向(200)峰位图
图4所示为样品的微观应变
与应力σ的变化关系曲线图,微观应变分别为0%、0.15%、0.39%、0.57%、0.82%、1.00%、1.24%、1.50%,对数据点进行拟合后得到曲线,可以发现样品的微观应变随着外加应力的增大呈线性增加,关系如式(6)。
(6)
对样品的伸长量进行监测,并计算样品的宏观应变,计算公式为:
(7)
其中
为薄带长度的变化量,
为薄带的原长,
为样品的宏观应变。
图5为样品的宏观应变
与应力σ的变化关系曲线图。样品的宏观应变分别为−0.31%、0.75%、1.98%、3.09%、4.365%、6.08%、8.50%、11.59%通过对数据点进行拟合发现应力较小时,样品的宏观应变能够与外加应力线性相关,关系如式(8),当应力继续增大,宏观应变总体上会与外加应力呈指数关系,关系如式(9)。
(8)
(9)
样品的磁各向异性、宏观应变随外加应力的变化是指数增大的,而微观应变与应力呈线性关系,与磁各向异性、宏观应变并不是线性关系。在以往的工作中,我们对于540℃应力退火后的薄带样品进行等温回火可以使得纳米晶的宏观应变有所减小,但仍有很大的残余,样品中的磁各向异性在多次回火后最终也会存在残余,而样品的晶格各向异性在第一次回火中明显减小,并可以在多次或长时间的回火过程中被逐渐消减,由拟合的曲线推导可以得出当样品的晶格各向异性减为0时,样品的磁各向异性仍有16%左右的残余 [16]。说明应力感生的磁各向异性并不完全由应力退火造成的纳米晶晶格各向异性导致,应还存在另一种应力退火导致的因素增大了样品的磁各向异性,且这种因素在大应力退火下对样品磁各向异性的影响更为显著。宏观应变远大于微观应变是由于非晶基底的蠕变导致的,且宏观应变与应力不
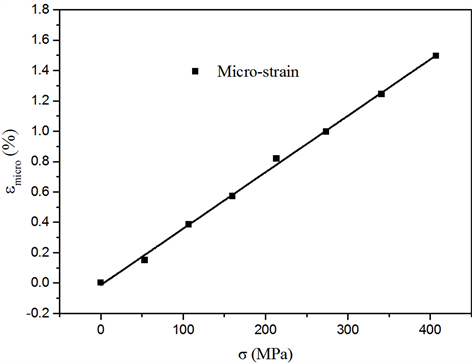
Figure 4. The relationship curve between micro strain and stress of the sample
图4. 样品的微观应变与应力的关系曲线图

Figure 5. The relationship curve between macro strain and stress of the sample
图5. 样品的宏观应变与应力的关系曲线图
呈线性关系,由此我们认为该因素是由非晶基底的蠕变带来的,并且不能通过多次回火或长时间的退火被消除。这里对自由退火和410 MPa应力退火样品中的纳米晶间隙进行了计算和比较。分析退火样品的XRD曲线得到晶化分数Vcr,并通过谢乐公式计算样品中纳米晶尺寸D:
(10)
这里的k是常数,取0.89,λ为测量时仪器给定的波长,B为XRD曲线(200)峰给定的半高宽FHWM,θ为XRD曲线上(200)峰对应的衍射角2θ的一半。得到自由退火样品的平均尺寸为9.51 nm,晶化分数为67.73%;应力退火样品的平均尺寸约为8.04 nm,晶化分数为69.45%。并结合样品的宏观应变和纳米晶的形状各向异性计算样品中纳米晶间隙δ,自由退火样品δ为7.95 nm,应力退火样品δ平行晶带方向为8.73 nm,垂直应力方向为3.98 nm,说明相比于自由退火,应力退火样品平行应力方向纳米晶间隙变大,垂直应力方向减小,造成了在垂直晶带方向上的纳米晶定向团聚,导致了横向纳米晶间的交换耦合作用增强,纵向纳米晶间的交换耦合作用减弱,从而增大了横向磁各向异性。
4. 结论
540℃退火的样品感生的磁各向异性与外加应力呈指数变化,样品的微观应变与外加应力满足线性关系。外加应力进行540℃退火时,非晶基底的蠕变会造成纳米晶横向之间距离减小,近邻纳米晶粒间的交换耦合作用增大,纵向纳米晶间隙增大,近邻纳米晶粒间的交换耦合作用减小,从而产生纳米晶分布各向异性,所以应力感生的磁各向异性中84%来自于外加应力退火感生的纳米晶晶格各向异性,其余16%是来自于无法被回火所消除的纳米晶分布各向异性。
基金项目
浙江省重点研发项目2018C01G2031345;国家自然科学基金项目51771083。