1. 引言
复合材料具有优异的比强度、比刚度性能,以及抗疲劳、耐腐蚀性能,在飞机结构上得到了广泛应用。碳纤维增强复合材料的增强相从T300级碳纤维发展到了T800级碳纤维,纤维性能实现大幅提升,使得复合材料层压板纤维控制性能的较大提高,更有利于结构减重;但是T800级碳纤维增强复合材料性能提升的同时带来了一些此前T300级碳纤维复合材料不存在的问题。例如通过对开孔拉–拉疲劳试验过程的观察,发现在较低应力比(疲劳峰值强度与静强度之比)下开孔拉伸试样边缘出现了大面积的分层现象,得到了与T300级碳纤维增强复合材料层压板不同的失效模式;因此T800级碳纤维增强复合材料试样边缘应力分析值得引起学者们的关注。
目前,许多学者对复合材料层压板在自由边处的层间应力开展了研究,包括解析法、有限差分方法以及有限元法。Salamon [1],Altus et al. [2],Pagano [3] 和Bhasker et al. [4] 等人采用有限差分法研究了复合材料层压板边缘层间应力问题,Wang [5] 等人则采用了有限元方法,Tang [6] [7] 等人采用边界层理论研究了复合材料层压板在拉伸载荷作用下的自由边效应问题。上述研究主要针对T300级碳纤维增强复合材料层压板,目前少有研究学者对T800级碳纤维增强复合材料层压板边缘应力开展深入研究。
本文针对T800级碳纤维增强复合材料开孔层压板,开展层间应力数值仿真分析研究,通过模拟不同宽径比的试样获取宽径比对开孔层压板在拉伸载荷作用下的边缘应力影响规律,为探究高强中模型复合材料开孔层压板边缘易分层问题提供分析支撑。
2. 数值仿真模型与方法
2.1. 数值模型
本文采用复合材料层内模型和层间模型构建开孔拉伸仿真模型;层内模型采用实体单元模拟;层间损伤模型采用界面单元(cohesive element)来模拟。有限元模型中开孔层压板尺寸、铺层与试验相同,层压板尺寸为300 mm × 36 mm × 2.24 mm,开孔直径为6 mm,铺层形式为[45/0/−45/90]2S。为了更好地预测层压板分层损伤,各层之间建立零厚度的Cohesive单元,采用三维8节点六面体线性减缩积分单元C3D8R对各铺层的层压板单元进行模拟,Cohesive单元为三维八节点粘性单元。开孔拉伸试样几何模型如图1所示。

Figure 1. Numerical model of open hole tensile specimen
图1. 开孔拉伸试样数值模型
2.2. 数值模型边界条件
本文数值模型边界条件为在开孔拉伸试样左端施加固支约束,在右端施加除1方向外的其余约束,同时在右端施加1方向的位移载荷,具体如图2所示。
2.3. 材料力学性能参数
本文采用T800级碳纤维增强复合材料进行数值模拟,表1为复合材料层压板基本力学性能参数。

Table 1. Basic mechanical property parameters of T800 carbon fiber reinforced composites
表1. T800级碳纤维增强复合材料基本力学性能参数
3. 数值仿真模型分析
3.1. 数值模型有效性验证
通过试验测得T800级碳纤维增强复合材料层合板开孔拉伸强度为495 MPa,其层压板尺寸为、铺层形式与上文所述相同。由本仿真模型计算得到的开孔拉伸强度为483.6 MPa,与试验结果相比误差为−2.3%,验证了本文提出数值模型的有效性。
3.2. 宽径比对开孔层压板边缘应力影响分析
根据对试验数据的分析发现,当开孔拉伸试样承受的平均应力水平达到350 MPa左右时,试样边缘出现分层。本仿真采用相同的参数设置分别计算宽度和孔径比(W/D)为6:1、7:1、8:1、9:1以及10:1 五种构型试样在350 MPa应力水平下试样边缘应力分布形式。
通过数值仿真分析得到了开孔拉伸试样各层间应力的响应云图以及失效云图。图3给出了宽径比为6开孔拉伸试样在350 MPa应力水平下,各层间应力的分布形式。通过界面的层间应力云图可发现在试验件的边缘和孔边存在较高的应力,特别是在孔两侧边缘的一倍厚度距离内应力集中非常明显,这将导致试样边缘更早的出现分层。图4给出了此模型在350 MPa应力水平下典型层间界面的损伤失效云图,由仿真结果可知在第3层与第4层(−45˚/90˚,以下称界面1)、第7层与第8层(−45˚/90˚,以下称界面2)、第9层与第10层(90˚/−45˚,以下称界面3)、第13层与第14层(90˚/−45˚,以下称界面4)之间的界面均在试样边缘出现了分层,而孔边均没有分层;由此说明试样的边缘效应对层压板层间失效产生了影响,不利于获取结构真实的性能;同时在刚度差异较大的层间易出现分层。由于层压板铺层的对称性,界面1和界面4的层间损伤比较类似,界面2和界面3的层间损伤比较类似,后续分析只给出界面1和界面2的层间损伤。
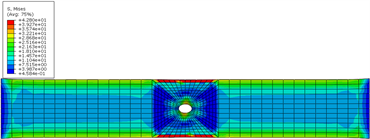 (a) 界面Mises应力云图
(a) 界面Mises应力云图 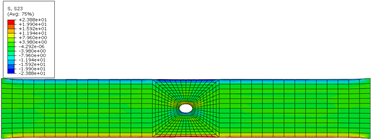 (b) 界面2~3方向剪切应力云图
(b) 界面2~3方向剪切应力云图
Figure 3. Stress nephogram of interlaminar interface of laminate
图3. 层压板层间界面应力云图
 (a) 界面1损伤云图
(a) 界面1损伤云图 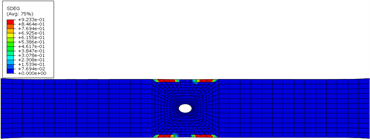 (b) 界面2损伤云图
(b) 界面2损伤云图 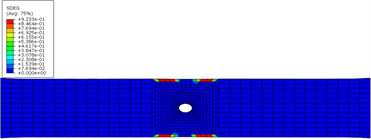 (c) 界面3层间损伤云图
(c) 界面3层间损伤云图 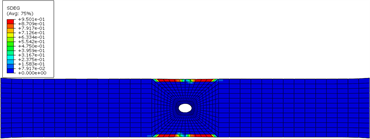 (d) 界面4层间损伤云图
(d) 界面4层间损伤云图
Figure 4. Typical interlaminar damage nephogram of laminate
图4. 层压板典型层间损伤云图
图5给出了宽径比为7开孔拉伸试样在350 MPa应力水平下,典型界面的损伤云图,图6为390 MPa应力水平下典型界面的损伤云图。可以发现随着宽径比由6增加到7,边缘分层损伤依然是比孔边损伤更早的产生,但是其需要更高的应力水平。
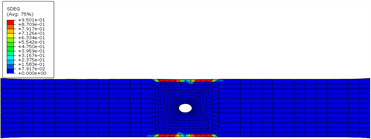 (a) 界面1损伤云图
(a) 界面1损伤云图 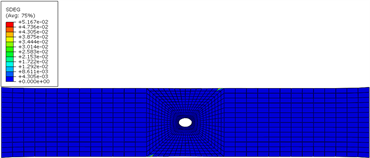 (b) 界面2损伤云图
(b) 界面2损伤云图
Figure 5. Typical interface damage of open hole tensile specimen (W/D = 7) at 350 MPa stress level
图5. 开孔拉伸试样(W/D = 7)在350 MPa应力水平下典型界面损伤
 (a) 界面1损伤云图
(a) 界面1损伤云图 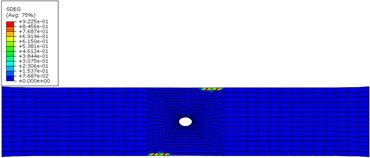 (b) 界面2损伤云图
(b) 界面2损伤云图
Figure 6. Typical interface damage of open hole tensile specimen (W/D = 7) at 390 MPa stress level
图6. 开孔拉伸试样(W/D = 7)在390 MPa应力水平下典型界面损伤
图7给出了宽径比为8开孔拉伸试样在350 MPa应力水平下,典型界面的损伤云图。可以发现随着宽度与孔径比由7增加到8,界面1孔边损伤和边缘初始损伤几乎同时出现,说明随着试验件宽度的增加边缘对界面损伤的影响变小,但边缘分层一直存在。
 (a) 界面1损伤云图
(a) 界面1损伤云图 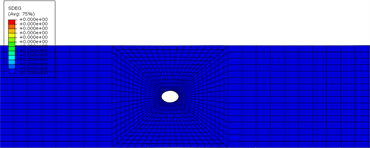 (b) 界面2损伤云图
(b) 界面2损伤云图
Figure 7. Typical interface damage of open hole tensile specimen (W/D = 8) at 350 MPa stress level
图7. 开孔拉伸试样(W/D = 8)在350 MPa应力水平下典型界面损伤
图8给出了宽径比为9开孔拉伸试样在350 MPa应力水平下,典型界面的损伤云图。可以发现随着宽度与孔径比由8增加到9,界面1孔边损伤和边缘初始损伤也几乎同时出现。
图9给出了宽径比为10开孔拉伸试样在350 MPa应力水平下,典型界面的损伤云图。可以发现随着宽度与孔径比由9增加到10,界面1孔边损伤和边缘初始损伤也几乎同时出现,边缘分层也存在。图10给出了宽径比为10开孔拉伸试样在412 MPa应力水平下,典型界面的损伤云图,随着载荷的增加,最终还是边缘首先发生分层失效。
 (a) 界面1损伤云图
(a) 界面1损伤云图  (b) 界面2损伤云图
(b) 界面2损伤云图
Figure 8. Typical interface damage of open hole tensile specimen (W/D = 9) at 350 MPa stress level
图8. 开孔拉伸试样(W/D = 9)在350 MPa应力水平下典型界面损伤
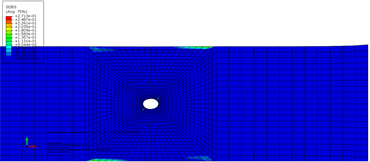 (a) 界面1损伤云图
(a) 界面1损伤云图 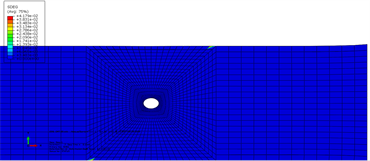 (b) 界面2损伤云图
(b) 界面2损伤云图
Figure 9. Typical interface damage of open hole tensile specimen (W/D = 10) at 350 MPa stress level
图9. 开孔拉伸试样(W/D = 10)在350 MPa应力水平下典型界面损伤
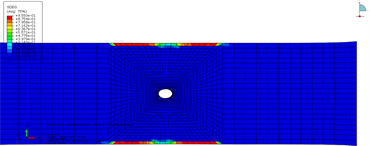 (a) 界面1损伤云图
(a) 界面1损伤云图 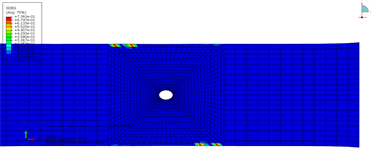 (b) 界面2损伤云图
(b) 界面2损伤云图
Figure 10. Typical interface damage of open hole tensile specimen (W/D = 10) at 412 MPa stress level
图10. 开孔拉伸试样(W/D = 10)在412 MPa应力水平下典型界面损伤
4. 结论
本文采用数值仿真分析方法对不同宽孔径比(W/D = 6~10)的开孔拉伸试样进行了仿真分析,通过对界面损伤失效过程的研究,发现边缘效应一直都存在,不会随着试验件宽度的增加而消失,但是会随着试验件宽度的增加而减弱对界面的影响,当宽径比达到8时(W/D = 8)会减弱对界面性能的影响,但最终边缘分层先于孔边分层发生。