基于层次分析法的城市沉降监测方案优选

An Optimal Selection Method of Urban Subsidence Monitoring Based on AHP

摘要: 沉降监测能够及时有效地反映地面高程变化，为城市快速发展提供重要的技术保障和决策建议。然而，城市沉降监测方案的选择往往受预算和区域等因素的影响，传统的方案选择随意性大且主观性强，难以达到观测精度和经济成本之间的平衡。针对上述问题，本文提出了基于层次分析法的城市沉降监测方案优选策略，通过判断矩阵构建、一致性检验以及影响因子权重计算，采用定性与定量相结合的决策分析方法对某城市地面沉降观测方案进行了综合评价。实验结果表明，利用GPS进行地面沉降监测的方案要优于传统水准测量，GPS沉降观测在满足精度的同时，有效节约了人力、时间和经济成本，相关成果可以为其他测绘工程方案选择提供借鉴。

Abstract: Subsidence monitoring can effectively reflect the changes of ground elevation in time and provide important technical support and decision-making suggestions for the rapid development of cities. However, the selection of urban subsidence monitoring is often affected by factors such as budget, region, etc., the traditional method is arbitrary and subjective, and difficult to balance the observa-tion accuracy and economic cost. To solve the above problems, this paper proposes an optimal se-lection method of urban subsidence monitoring based on AHP. Through the construction of judg-ment matrix, consistency test and weight calculation of influence factors, the qualitative and quan-titative decision analysis method is used to comprehensively evaluate the land subsidence observa-tion scheme in a specific city. The experimental results show that the scheme of using GPS to moni-tor the land subsidence in this city is better than the traditional leveling. The GPS observation can meet the accuracy and effectively save manpower, time and economic costs. The relevant results can provide reference for the selection of other surveying and mapping projects.

1. 引言

随着社会经济的不断发展，城市化的脚步逐渐加快，城镇人口数量日益增多，人们对于城市物质资源需求量也急剧增加，最典型的就是城市地下水的过度开采导致地表发生不同程度的沉降，严重影响着城市的可持续发展，可见，做好城市地表的沉降监测对地区的稳定发展意义重大 [1] [2]。

目前来讲，城市地面沉降观测应用比较广泛的方法有传统水准测量和GPS静态监测，上述两种方法的优缺点也是显而易见的 [3] [4] [5]。传统水准测量用于沉降观测具有测量精度高、观测设备便宜、内业数据处理简单等优点，但在大范围城市地面沉降监测中外业工作量大且耗费人力物力 [6] [7] [8]。GPS监测具有自动化程度高、全天候监测等优点但仪器相对昂贵且卫星信号受外界因素干扰较大 [9] [10] [11] [12]。一项优秀的沉降监测方案，不仅要在技术上安全可靠，还需要考虑经济和环境等诸多要素，这其中既有可以定量分析的要素，同时一些要素难以定量分析，所以需要根据专家实践理论和个人经验结合给出合理的选择。然而，现有通过专家定性分析的方式进行沉降观测方案选择随意性大且主观性强，难以为决策者提供科学参考。

因此，本文提出了基于层次分析法的城市沉降监测方案优选方法，给出不同方案中监测工作的影响因素，并根据专家经验知识构建城市地面沉降监测层次结构模型以及相应的判断矩阵，最后以MATLAB为解算工具对结果进行一致性检验，得到不同城市地面沉降监测方案的权重，并成为最终方案优选的决策依据。

2. 方法

2.1. 城市地面沉降监测层次结构模型

层次分析法(Analytic Hierarchy Process, AHP)首先将目标层转化为不同的层次结构，利用数学矩阵分析并求解评价指标 [13] [14] [15] [16]。本文根据大面积沉降监测的基本步骤，从测量精度、方案预算、选点布网、测量误差和数据处理五个方面逐一分析沉降监测的影响因素，构建了以层次结构模型为基础的城市沉降监测方案，如图1所示。

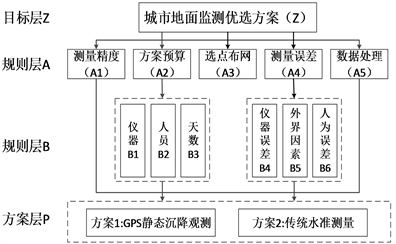
Figure 1. Urban settlement monitoring scheme structure hierarchy diagram

图1. 城市沉降监测方案结构层次图

规则层A主要包括5个因素。其中，测量精度是进行沉降观测方案选择的关键影响因素；方案预算所涉及的经济成本是影响整个沉降监测工程的重要因素，主要包括测量仪器、测量人员和工作天数等，所以方案设计时同样需要把经济和节约成本考虑进去；数据处理会影响整个监测方案的时间，不同方案的数据处理差异较大，在本文中主要考虑基线解算和平差计算；选点布网对于GPS监测和水准测量的要求不一致，所以也纳入考虑范围；测量误差与测量精度类似，同样是方案选择的重要影响因素。

由于大面积沉降监测方案相对复杂，所以本文将原有的规则层分支得到一个子准则层B，通过更多影响因素的加入可以得到更加准确客观的分析结果。其中，方案预算可以分为仪器成本的投入，人员的数量以及完成整个沉降监测方案所需要的天数；测量的误差大体归位三类，即三个影响因子：仪器本身误差，各种外界因素引起的误差和人为产生的误差。

2.2. 基于专家经验构建判断矩阵

当确定目标层、规则层和决策层之间的隶属关系后，则需要针对目标构建判断矩阵。在判断矩阵构造过程中，为了使得影响因子进行定量化表示，本文基于专家经验的基础上，本文参考1~9尺度标度法对影响因子进行两两比较 [16] [17]，如表1所示。其中1表示两因子具有同等重要性，3、5、7、9分别表示两因子中前者比后者稍微、明显、强烈、极端重要，余下数字则表示为中间值。

Table 1. Meaning of scale 1~9

表1. 1~9尺度标度含义

由此可以得到判断矩阵A为：

$A=\left[\begin{array}{cc}\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}& \begin{array}{cc}\cdots & a_{1n}\\ \cdots & a_{2n}\end{array}\\ \begin{array}{cc}⋮& ⋮\\ a_{n1}& a_{n1}\end{array}& \begin{array}{cc}\ddots & ⋮\\ \cdots & a_{nn}\end{array}\end{array}\right]$

2.3. 层次单排序及一致性检验

权值W代表层次单排序中影响程度大小，分别记作： $w_1,w_2,\cdots ,w_n$，具体解算过程如下：

首先，将判断矩阵A中的影响因子按列进行归一化处理，如公式(1)所示：

$a_{ij}=\frac{a_{ij}}{{\displaystyle {\sum }_{i=1}^n{a}_{ij}}}$ (1)

其中， $a_{ij}$ 表示归一化后的向量， $a_{ij}$ 表示判断矩阵中的元素。其次，将归一化的 $a_{ij}$ 按行相加得到新的 $w_i$ 向量，如公式(2)所示：

$w_i={\displaystyle {\sum }_{j=1}^n{a}_{ij}}$ (2)

然后，将新得到的 $w_i$ 向量进行归一化处理可得到 $w_i$，如公式(3)所示：

$w_i=\frac{w_i}{{\displaystyle {\sum }_{j=1}^n{w}_i}}$ (3)

式中， $w_i$ 即为所求的特征向量，在此基础上采用公式(4)计算最大特征根 ${\lambda }_{\max }$。

${\lambda }_{\max }={\displaystyle {\sum }_{i=1}^n\frac{{\left[Aw\right]}_i}{n{w}_i}}$ (4)

其中A表示判断矩阵，n表示矩阵的维数，在此基础上，利用公式(5)进行一致性检验指标CI计算。

$CI=\frac{{\lambda }_{\max }-n}{n-1}$ (5)

同时一致性指标RI的具体取值如表2所示。

Table 2. RI values

表2. RI取值

$CR=\frac{CI}{RI}$ (6)

如公式(6)所示，CR表示一致性比率，当它的值比0.1小时，通常认为所构建的判断矩阵是合理的。

2.4. 层次总排序及一致性检验

层次总排序就是用来确定某层要素相对于总体目标重要性的过程。具体可采用公式(7)计算。

$P_i={\displaystyle {\sum }_{j=1}^m{a}_j{b}_{ij}}$ (7)

其中 $P_i$ 表示层次总排序的权重值，具体来讲，如公式(8)所示。

$\begin{array}{l}{B}_1:a_1{b}_{11}+a_2{b}_{12}+\cdots +a_m{b}_{1m}\\ B_2:a_1{b}_{21}+a_2{b}_{22}+\cdots +a_m{b}_{2m}\\ ⋮\\ B_n:a_1{b}_{n1}+a_2{b}_{n2}+\cdots +a_m{b}_{nm}\end{array}$ (8)

采用公式(9)来表示层次总排序的一致性比率CR。

$CR=\frac{a_{1}C{I}_1+a_{2}C{I}_2+\cdots +a_{m}C{I}_m}{a_{1}R{I}_1+a_{2}R{I}_2+\cdots +a_{m}R{I}_m}$ (9)

当CR值比0.1小时，则说明层次总排序合理，否则不合理。

3. 案例分析

本文以某城市地面沉降为案例进行监测方案优化选择实验，分析确定了该城市地面沉降监测方案优选层次模型中各层的判断矩阵。如图2所示。

Figure 2. The monitoring scheme selects the judgment matrix of each level

图2. 监测方案优选各层次判断矩阵

图3表示利用MATLAB计算得出的各个矩阵的最大特征值和特征向量结果。

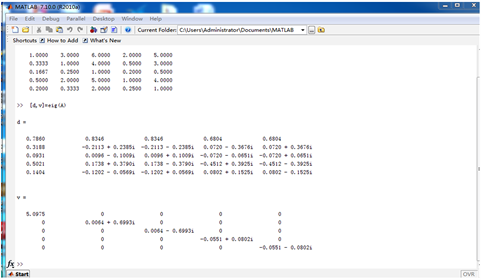
Figure 3. Matlab calculation results

图3. MATLAB计算结果

针对判断矩阵A-A，其中最大特征值 ${\lambda }_{\max }=5.098$，归一化特征向量为 $w=\left[0.427,0.173,0.05,0.273,0.076\right]$，一致性指标为 $CI=0.0245$，一致性比率 $CR=0.022<0.1$，表明判断矩阵合理且结果通过一致性检验。同理，可以求出其他矩阵的一致性比率。然后可以分别求出P₁对于目标层Z层的权值为0.57，P₂对于目标层Z层的权值为0.43，可以看出方案一P₁即利用GPS进行该城市的地面沉降监测要优于方案二P₂即水准测量，所以选择方案一。

4. 结束语

本文采用了层次分析法进行城市沉降监测方案优选，并以某城市地面沉监测为例开展了案例分析，结果表明在该城市采用GPS进行沉降监测更加科学合理，其主要原因是GPS用于城市地面沉降监测不但可以扩大监测面积、降低监测成本还可以提高监测灵活性。同时可以看出，采用层次分析法可以降低方案选择的难度和人主观因素的影响，提高最终决策的客观性和科学性。