基于指数平方误差风险控制下的最佳投资策略研究

The Study of the Optimal Investment Strategy Based on Risk-Management Model

摘要: 经典的马柯威茨投资组合模型以方差作为风险度量，不能区别对待期望两侧投资者的不同感受。考虑指数平方误差的优越性，在均值-CVaR模型的基础上，使用指数平方误差作为风险度量，即只考虑其投资在损失的一侧来做出新的投资组合优化模型。进一步讨论了指数平方误差损失模型的有效前沿，并以中国工商银行等股票价格为实例做了实证分析，结果表明基于指数平方误差风险控制下的投资策略具有很好的适应性。

Abstract: The classical Markowitz portfolio model measuring risk with variance, it does not deal with the different feelings of investors on both expect sides. This paper uses an improved model of Markowitz portfolio selection model, that is, Exponential Squared Loss as a risk measure, which is based on the Mean-CVaR model, to consider their investment only in the side of the loss in order to get a better portfolio. Moreover, we discuss the efficient frontier of Exponential Squared Loss model, and then make an empirical analysis taking price of Industrial and Commercial Bank of China as an example. The results indicate that the investment strategy based on Exponential Squared Loss model has good adaptability.

1. 引言

随着经济全球化发展，金融资本市场频繁波动，需要发展新的风险度量模型引导资本有效配置，其中CVaR就是建立在VaR基础上新发展起来的风险度量模型。目前，尽管CVaR理论研究与实证分析技术手段日趋成熟，但随着金融资本市场的快速发展，CVaR模型为适应社会经济快速发展，其理论及应用还有待更深入挖掘，以解决更复杂的经济现象。Uryasevyu与Rochafellar [1] 首次提出了CVaR模型，并论证了CVaR模型与经典的VaR模型的一致性；Pflug [2] 从证券投资优化问题出发，论证了CVaR的一致性风险度量特性。Pownall [3] 应用CVaR对亚洲金融危机中证券市场进行实证研究。国内学者陈剑利等 [4] 等利用CVaR风险度量模型构造投资函数；王建华 [5] 等则通过分析VaR模型风险度量不足，利用CVaR理论提出度量和控制金融风险的新方法。众所周知，资本损失的不确定性和资本收益的不确定性的风险度量通常是用方差来描述的，然而方差作为风险度量使投资收益两侧出现不对称这种固有的缺陷 [6]。为避免类似问题的出现，采用指数平方误差作为风险度量是可以解决的。不同于经典CVaR模型，本文主要考察风险控制过程中的投资策略，着重考察单侧风险度量，并在此基础上提出基于方差和指数平方误差最小化的投资组合效用决策模型。通过对比分析，得到本文研究的主要结论：对资产选择决策时，指数平方误差模型的投资结果要优于均值–方差模型。

2. 基于条件风险价值(CVaR)的投资组合优化模型

条件风险价值(CVaR) [2] [3] [4] [5] [6] 理论是指在一定的时间T内正常市场条件下和一定置信度水平为 $\alpha$ 的情况下，对收益分布尾部 $1-\alpha$ 部分求条件期望，其转为为数学问题为：

$\text{CVaR}\left(Y\right)=E\left(Y|Y\ge {\text{VaR}}_a(\; Y\; )\right)$

CVaR具有以下性质：

1) 平移不变性 ${\text{CVaR}}_a\left(Y+C\right)={\text{AVaR}}_a\left(Y\right)+C$

2) 正齐性 ${\text{CVaR}}_a\left(cy\right)=c\text{CVaR}\left(y\right),c>0$

3) 凸性对任意随机变量 $y_1,y_2$，当 $0<\lambda <1$ 时，有：

$\text{CVaR}\left(\lambda y_1+\left(1-\lambda \right)y_2\right)\le \lambda \text{CVaR}\left(y_1\right)+\left(1-\lambda \right)\text{CVCaR}(\; y\; 2\; )$

定义1 假设k种证劵组成的投资组合中，各种证劵所占的投资比例为： $x={\left(x_1,\cdots ,x_k\right)}^{\text{T}}$ 其中 ${\displaystyle \underset{i=1}{\overset{k}{\sum }}{x}_i=1}\left(x_i\ge 0\right)$。投资组合的回报为： $R={\displaystyle \sum x_i{\gamma }_i}$，这里 ${\gamma }_i$ 表示各项投资的回报率。如果最低回报率用c表示，则经典的CVaR模型表示为：

$\begin{array}{l}\min \text{CVaR}\left(-x^{\text{T}}\gamma \right)\\ \text{s}\text{.t}\{\begin{array}{l}{x}^{\text{T}}F\left(\gamma \right)\ge c\\ {\displaystyle \sum x_i}=1\\ x_i\ge 0\end{array}\end{array}$

2.1. 均值–方差模型的有效前沿

一般的，最优证券组合从期望上要求其收益最大的同时具有最小的不确定性。如何在这一组相互矛盾的命题中寻求最佳均衡点(trade-off)是资产组合的核心问题。基于收益方对待风险态度的差异，会产生不同的投资策略：风险爱好者期望组合的收益率达到最大；风险避规者则更多的期望有效控制风险。以此，基于风险的差异，可以得到均值–方差模型有效前沿的定义。

定义2 如果投资组合 $X^{*}$ 为置信水平为 $\beta \left(0<\beta <1\right)$ 的均值–方差有效前沿，当且仅当不存在组合 $X^{**}\in X$ 使得 $E\left(r_{X^{**}}\right)\ge E\left(r_{X^{*}}\right)$ 和 $\sigma \left(r_{X^{**}}\right)\le \sigma \left(r_{X^{*}}\right)$ 同时成立，且至少有一个严格不等式。

推论1 取 $E\left(r_X\right)=r_0$，则求解以下线性约束二次规划问题：

$\begin{array}{l}\min {\sigma }^2\left(r_x\right)=X^{\text{T}}VX\\ \text{s}\text{.t}\{\begin{array}{l}E\left(r_x\right)=X^{\text{T}}R=r_0\\ X^{\text{T}}e=1\end{array}\end{array}$

就能求出前沿上的点的问题，即证劵组合在前沿上最小的方差。

定理1 前沿上的两个证劵组合协方差为： $Cov\left(r_0,r_1\right)=X^{\text{T}}V{X}_1=\frac{C}{D}\left(r_0-\frac{A}{C}\right)\left(r_1-\frac{A}{C}\right)+\frac{1}{C}$。

当 $r_0=r_1$ 时，证劵组合的方差 $\sigma {\left(r_X\right)}^2=\frac{C}{D}{\left(E\left(r_X\right)-A/C\right)}^2+\frac{1}{C}$，即 $\frac{\sigma {\left(r_X\right)}^2}{1/C}-\frac{{\left(E\left(r_X\right)-A/C\right)}^2}{D/C^2}=1$ 的上半支就是均值–方差模型的有效前沿。

证明：

为求解该问题，构造恰当的拉格朗日函数：

$L\left(X,\lambda ,\mu \right)=X^{\text{T}}VX+\lambda \left(r_0-X^{\text{T}}R\right)+\mu \left(1-X^{\text{T}}e\right)$

从而有：

$\{\begin{array}{l}\frac{\partial L}{\partial X^{\text{T}}}=2VX-\lambda R-\mu e=0\\ \frac{\partial L}{\partial \lambda }=r_0-X^{\text{T}}R=0\\ \frac{\partial L}{\partial \mu }=1-X^{\text{T}}e=0\end{array}$ (1)

显然，V是正定矩阵。解此方程组，可以得到： $\lambda =\left(C{r}_0-A\right)/D,\mu =\left(B-A{r}_0\right)/D$，其中 $A=e^{\text{T}}{V}^{\text{T}}R=R^{\text{T}}{V}^{-1}e,B=R^{\text{T}}{V}^{-1}R,C=e^{\text{T}}{V}^{-1}e,D=BC-A^2>0$。

将 $\lambda ,\mu$ 代入(1)式，得到在指定收益 $r_0$ 下方差最小的证劵组合：

$X=\frac{r_{0}C-A}{D}{V}^{-1}R+\frac{B-r_{0}A}{D}{V}^{-1}e$ (2)

类似的，指定另外一个收益 $r_1$，在前沿上的证劵组合为：

$X_1=\frac{r_{1}C-A}{D}{V}^{-1}R+\frac{B-r_{1}A}{D}{V}^{-1}e$ (3)

由(2) (3)式得到前沿上的两个证劵组合协方差为： $Cov\left(r_0,r_1\right)=X^{\text{T}}V{X}_1=\frac{C}{D}\left(r_0-\frac{A}{C}\right)\left(r_1-\frac{A}{C}\right)+\frac{1}{C}$。 □

现以标准差作为横轴，均值作为纵轴构成一坐标系，其中图像是以 $\left(0,A/C\right)$ 为中心， $E\left(r_X\right)=A/C\pm \sqrt{D/C}\sigma \left(r_X\right)$ 为渐近线的开口向右的双曲线，如图1所示。

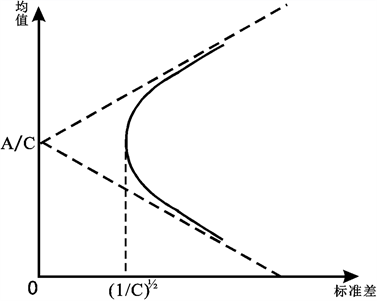
Figure 1. Efficient frontier of mean-variance model

图1. 均值–方差模型有效前沿曲线

图1所示，双曲线的顶点表示最小方差证劵组合。事实上，无差异曲线可以描述两个截然不同的投资者I₁，I₂所愿意承担的风险无差异组合，如图2所示。图中点M与点N为最佳投资组合的最优点。

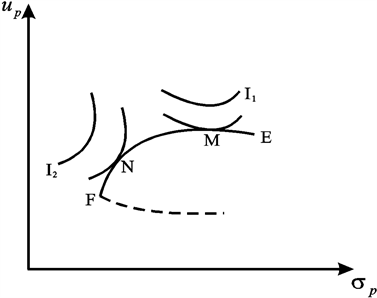
Figure 2. Schematic map of choosing securities portfolio

图2. 投资者选择证劵组合示意图

3. 新的风险度量准则——指数平方误差风险

经典的马柯威茨均值–方差模型度量风险的参数为资产收益率的方差，其试图平衡风险投资领域中资产组合的预期收益和风险这两个核心问题 [6] - [11]。然而由于方差作为风险度量存在的不足，需要对风险度量的准则作进一步改进 [7] [8] [10] [11]，因此获得指数平方误差风险度量的概念。

定义3 设 $r_i$ 表示第i个证劵投资， $R_i$ 表示其期望收益，用 $x_i$ 表示第i项投资的额度 $i=1,2,\cdots ,n$，则对于单个投资而言投资组合的风险指数 [7]：

$\varphi \left(u_i\right)=1-E\left[\exp \left(-u_i^2/\gamma \right)\right]$

其中， $u_i=R_i-x_i^{\text{T}}{r}_i$， $\gamma$ 为控制估计量的鲁棒性程度的指数。

注1 较小的 $\gamma$ 在这些估计量中将限制异常值的影响，尽管它也降低了估计量的灵敏度。

注2 当 $\gamma$ 非常大时， $\varphi \left(u\right)\approx u^2/\gamma$，此时，该估计量类似于最小二乘估计；

当 $\gamma$ 非常小时，通过对 $u_i=R_i-x_i^{\text{T}}{r}_i$ 的大量的绝对值可以观测到 ${\varphi }_{\gamma }\left(u_i\right)$ 的大额损失，此时，该估计量对参数 $R_i$ 的估算有一些影响。

因此，较小的 $\gamma$ 在这些估计量中将限制异常值的影响，尽管它也降低了估计量的灵敏度。

定义4 一个估计量在有限样本下添加的击穿点被定义为：

$BP\left({\stackrel{⌢}{\beta }}_n;D_{n-m}\right)=\min \left\{\frac{m}{n}:\underset{D_m}{\sup }\Vert \stackrel{⌢}{\beta }\left(D_n\right)-\stackrel{⌢}{\beta }\left(D_{n-m}\right)\Vert =\infty \right\}$

其中， ${\stackrel{⌢}{\beta }}_n$ 是d维向量的未知参数， $D_n=\left(D_1,\cdots ,D_n\right)$， $D_i=\left(x_i,Y_i\right)$， $D_{n-m}=\left\{D_{m+1},\cdots ,D_n\right\}$， $\frac{m}{n}$ 是 $D_n$ 中的坏点比例， $\stackrel{⌢}{\beta }\left(D_n\right)$ 是基于样本 $D_n$ 回归估计， $\Vert \cdot \Vert$ 是欧几里德范数。

注3 定义3提供了下界的击穿点，这个界依赖于初始估计和调整参数 ${\gamma }_n$ 的击穿点。

注4 如果 ${\tilde{\beta }}_n$ 是渐近击穿点的1/2倍鲁棒估计且 ${\gamma }_n$ 使得 $\zeta \left(\gamma \right)\in \left(0,1\right]$，那么 $BP\left({\stackrel{⌢}{\beta }}_n;D_{n-m};{\gamma }_n\right)$ 是渐近的1/2。

定义5 用风险指数作为风险度量因子，则这种风险度量下的风险模型 [7] 表示为：

$\begin{array}{l}\max E\left(u\right)=E\left(x_1{r}_1+x_2{r}_2+\cdots +x_n{r}_n\right)\\ \text{s}\text{.t}\{\begin{array}{l}E\left(\varphi \left(u\right)\right)\le c\\ {\displaystyle \underset{i=0}{\overset{n}{\sum }}{x}_i=1}\\ x_i\ge 0\end{array}\end{array}$ (4)

3.1. 指数平方误差损失模型的有效前沿

由定义2及推论1有：取 $E\left(\varphi \left(u\right)\right)=u_0$，求解以下线性约束二次规划问题：

$\begin{array}{l}\max {\sigma }^2\left(\varphi \left(u\right)\right)=X^{\text{T}}VX\\ \text{s}\text{.t}\{\begin{array}{l}E\left(\varphi \left(u\right)\right)=X^{\text{T}}R=u_0\\ X^{\text{T}}e=1\end{array}\end{array}$

就可求得前沿上的点的问题，进而可求得在前沿上的方差最小的证劵组合。

定理2 前沿上的两个证劵组合协方差为：

$Cov\left(u_0,u_1\right)=X^{\text{T}}V{X}_1=\frac{C}{D}\left(u_0-\frac{A}{C}\right)\left(u_1-\frac{A}{C}\right)+\frac{1}{C}$

当 $u_0=u_1$ 时，证劵组合的方差 $\sigma {\left(\varphi \left(u\right)\right)}^2=\frac{C}{D}{\left(E\left(\varphi \left(u\right)\right)-A/C\right)}^2+\frac{1}{C}$，即 $\frac{\sigma {\left(\varphi \left(u\right)\right)}^2}{1/C}-\frac{{\left(E\left(\varphi \left(u\right)\right)-A/C\right)}^2}{D/C^2}=1$ 的上半支曲线即为对应的均值–方差模型的有效前沿。

证明：

一般的，引入以下的拉格朗日函数：

$L\left(X,\lambda ,\mu \right)=X^{\text{T}}VX+\lambda \left(u_0-X^{\text{T}}R\right)+\mu \left(1-X^{\text{T}}e\right)$

从而有：

$\{\begin{array}{l}\frac{\partial L}{\partial X^{\text{T}}}=2VX-\lambda R-\mu e=0\\ \frac{\partial L}{\partial \lambda }=u_0-X^{\text{T}}R=0\\ \frac{\partial L}{\partial \mu }=1-X^{\text{T}}e=0\end{array}$ (5)

显然，V是正定矩阵。解此方程组，可以得到： $\lambda =\left(C{u}_0-A\right)/D,\mu =\left(B-A{u}_0\right)/D$。

其中 $A=e^{\text{T}}{V}^{\text{T}}R=R^{\text{T}}{V}^{-1}e,B=R^{\text{T}}{V}^{-1}R,C=e^{\text{T}}{V}^{-1}e,D=BC-A^2>0$。

将 $\lambda ,\mu$ 代入(5)式，得到在指定收益 $u_0$ 下方差最小的证劵组合：

$X=\frac{u_{0}C-A}{D}{V}^{-1}R+\frac{B-u_{0}A}{D}{V}^{-1}e$ (6)

类似的，指定另外一个收益 $r_1$，在前沿上的证劵组合为：

$X_1=\frac{u_{1}C-A}{D}{V}^{-1}R+\frac{B-u_{1}A}{D}{V}^{-1}e$ (7)

由(6) (7)式得到前沿上的两个证劵组合协方差为： $Cov\left(u_0,u_1\right)=X^{\text{T}}V{X}_1=\frac{C}{D}\left(u_0-\frac{A}{C}\right)\left(u_1-\frac{A}{C}\right)+\frac{1}{C}$。□

3.2. 指数平方误差损失模型中 $\gamma$ 的选取

选取 $\gamma$ 的整个过程列为以下几个步骤 [9]：

1、 找伪离群值集的样本

令 $D_n=\left\{\left(x_1,R_1\right),\cdots ,\left(x_n,R_n\right)\right\}$，计算 $v_i\left({\stackrel{⌢}{\beta }}_n\right)=R_i-x_i^{\text{T}}{\stackrel{⌢}{\beta }}_n,i=1,\cdots ,n$ 和 $S_n=1.4826\times media{n}_i\left|v_i\left({\stackrel{⌢}{\beta }}_n\right)-media{n}_j\left({\stackrel{⌢}{\beta }}_n\right)\right|$，然后采取伪异常，让 $D_m=\left\{\left(x_i,R_i\right):\left|v_i\left({\stackrel{⌢}{\beta }}_n\right)\right|\ge 2.5S_n\right\}$，其中 $m=\#\left\{1\le i\le n:\left|v_i\left({\stackrel{⌢}{\beta }}_n\right)\right|\ge 2.5S_n\right\}$， $D_{n-m}=D_n/D_m$。

2、更新调整参数 ${\gamma }_n$

设 ${\gamma }_n$ 是 $\det \left(\stackrel{⌢}{V}\left(\gamma \right)\right)$ 在集合 $G=\left\{\gamma :\zeta \left(\gamma \right)\in \left(0,1\right]\right\}$ 中的极小值，其中 $\zeta \left(\gamma \right)$ 的定义为 $\zeta \left({\gamma }_n\right)=\frac{2m}{n}+\frac{2}{n}{\displaystyle \underset{i=m+1}{\overset{n}{\sum }}\left\{1-E\left[\exp \left(-u_i^2/\gamma \right)\right]\right\}\left\{v_i\left({\tilde{\beta }}_n\right)\right\}}$，其中， $u_i=R_i-x_i^{\text{T}}{r}_i$， $\zeta \left({\gamma }_n\right)$ 是 $\left(0,2\right]$ 的实数。 $\stackrel{⌢}{V}\left(\gamma \right)={\left\{{\stackrel{⌢}{I}}_1\left({\stackrel{⌢}{\beta }}_n\right)\right\}}^{-1}{\Sigma }_2{\left\{{\stackrel{⌢}{I}}_1\left({\stackrel{⌢}{\beta }}_n\right)\right\}}^{-1}$，其中，

${\stackrel{⌢}{I}}_1\left({\stackrel{⌢}{\beta }}_n\right)=\frac{2}{\gamma }\left\{\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\exp \left(-v_i^2\left({\stackrel{⌢}{\beta }}_n\right)/\gamma \right)}\cdot \left(\frac{2v_i^2\left({\stackrel{⌢}{\beta }}_n\right)}{\gamma }-1\right)\right\}\times \left(\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i{x}_i^{\text{T}}}\right)$

${\Sigma }_2=\mathrm{cov}\left\{\exp \left(-v_1^2\left({\stackrel{⌢}{\beta }}_n\right)/\gamma \right)\frac{2v_1\left({\stackrel{⌢}{\beta }}_n\right)}{\gamma }{x}_1,\cdots ,\exp \left(-v_n^2\left({\stackrel{⌢}{\beta }}_n\right)/\gamma \right)\frac{2v_1\left({\stackrel{⌢}{\beta }}_n\right)}{\gamma }{x}_n\right\}$

3、根据固定的 ${\lambda }_{nj}=\log \left(n\right)/\left(n\left|{\stackrel{⌢}{\beta }}_n\right|\right)$ 和在步骤2中确定的 ${\gamma }_n$ 使 ${\mathcal{l}}_n\left(\beta \right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}\exp \left\{-{\left(R_i-x_i^{\text{T}}\beta \right)}^2/{\gamma }_n\right\}-n{\displaystyle \underset{j=1}{\overset{d}{\sum }}{p}_{{\lambda }_{nj}}\left(\left|{\beta }_j\right|\right)}}$ 最大化来更新 ${\stackrel{⌢}{\beta }}_n$。

取MM估计值 ${\tilde{\beta }}_n$ 作为初始估计值，即 ${\stackrel{⌢}{\beta }}_n={\tilde{\beta }}_n$，然后重复步骤1~3，直到 ${\stackrel{⌢}{\beta }}_n$ 和 ${\gamma }_n$ 收敛。

根据Matlab软件的计算结果，得到 $\gamma =3.9579$。

4. 实证研究

4.1. 数据的收集

本文所搜集的实证数据的时间跨度是从2016年1月至2018年12月三年内共计36个月，包括工商银行(601398)、天山股份(000877)、兰花科创(600123)、贵州茅台(600519)、中国平安(601318)这5支股票的个股回报率，具体数据如表1，其平均收益率如表2。

Table 1. The monthly return data about 5 stocks

表1. 5支股票的月收益率数据(%)

Table 2. Average returns ratio of individual share

表2. 个股平均收益率(%)

4.2. 数据的分析与结果

通过利用Matlab中正态检验函数jbtest检验所考察的数据，在一定的显著性水平下，数据均满足正态性假设。因此考察在该组合下经典的均值–方差模型与改进的指数平方误差损失模型条件下的投资策略，并对其结果作比较。

A、求解经典的均值–方差模型，得到对应的协方差矩阵为：

$V=\left(\begin{array}{ccccc}0.0016& 0.0023& 0.0022& -0.0002& 0.0004\\ 0.0023& 0.0218& 0.0083& 0.0040& 0.0016\\ 0.0022& 0.0083& 0.0137& 0.0022& 0.0006\\ -0.0002& 0.004& 0.0022& 0.0085& 0.0000\\ 0.0004& 0.0016& 0.0006& 0.0000& 0.0086\end{array}\right)$

利用matlab软件求解，得到其权重为： $X^{\text{T}}=\left(0.0639,0.4698,0.2391,0.1254,0.0478\right)$。

B、求解改进的指数平方误差损失模型，得到对应的协方差矩阵为：

$H^{-}=\left(\begin{array}{ccccc}0.0001& 0.0001& 0.0002& -0.0000& 0.0000\\ 0.0001& 0.0016& 0.0006& 0.0003& 0.0001\\ 0.0002& 0.0006& 0.0009& 0.0001& 0.0000\\ -0.0000& 0.0003& 0.0001& 0.0006& 0.0000\\ 0.0000& 0.0001& 0.0000& 0.0000& 0.0006\end{array}\right)$

利用matlab软件求解，得到其权重为： $X^{\text{T}}=\left(0.0553,0.5002,0.2852,0.1245,0.0349\right)$。

显然，经典的均值方差模型(A)与改进的指数平方误差损失模型(B)相比较，5只股票的投资比例发生了微小变化。通过对这两种不同的模型所得结果表明相对按照均值–方差模型来投资而言，按照指数平方损失模型发生损失的概率会更小。因此，投资者的投资更倾向利用指数平方损失模型。该组合的期望收益率 $r_x$ 从−0.008开始，每次递增步长为0.00001，到0.012为止共201个点，在Matlab软件平台下，分别得到了经典均值方差模型以及基于指数平方损失最小准则下，该组合的有效前沿边界曲线，如图3。

Figure 3. The effective frontier of stocks in different algorithms, where the red line representing Exponential Squared Loss algorithms and the blue line representing the classic Markowitz algorithms

图3. 两种不同算法下，股票的有效前沿，其中红色曲线为基于指数平方损失最小准则下的投资组合的有效前沿曲线，蓝色为经典的马柯威茨投资组合有效前沿曲线。

在期望收益相同时，经典的均值方差模型(A)所承担的风险要远远大于基于指数平方损失最小准则下的投资组合策略(B)，因此，指数平方损失最小准则能为投资者有效地规避风险。

基金项目

海南省自然科学基金(120RC451)，国家自然科学基金(11761025, 11901114)，广东省教育厅青年创新人才类(2017KQNCX081)，广州市科技创新一般项目(201904010010)，中山大学广东省计算科学重点实验室开放课题基金资助(2018001)，海南省研究生创新科研课题项目(Hys2019-59)。