非线性本构关系下两端固定铰支梁的弯曲变形

Bending Deformation of Hinged-Fixed Beams at Both Ends under Nonlinear Constitutive Relations

摘要: 本文基于经典梁理论，假设弹性模量与应变成线性关系(本构关系非线性)，推导了受铅垂均布载荷作用的两端固定铰支梁弯曲的基本方程。并对基本方程及边界条件无量纲化，以使其具有一般性。然后采用数值法求解该问题无量纲基本方程的数值结果。分析了大挠度和小挠度两种情况下本构关系非线性和铅垂分布载荷对梁弯曲变形以及中性轴位置的影响并进行比较。

Abstract: Based on the classical beam theory, this paper assumes that the elastic modulus and the strain become a linear relationship (non-linear constitutive relationship), and derives the basic equation for the bending of a fixed hinge beam at both ends under a vertical uniform load. And the basic equations and boundary conditions are dimensionless to make them general. Then, the numerical method is used to solve the numerical results of the non-dimensional basic equation of the problem. The influence of the nonlinear constitutive relationship and the vertical distributed load on the bending deformation of the beam and the position of the neutral layer in the two cases of large deflection and small deflection are analyzed and compared.

1. 引言

经典力学研究方法中认为材料的弹性模量在变形过程中是不变的，但是大量研究表明有很多材料受拉和受压时具有不同的弹性模量。实际工程中构件可能存在受拉和受压交替变换的情况，因此对拉压不同弹性模量的研究是很有必要的。不少研究者在分析弹性体变形时将受拉和受压分成两个阶段，然后分别将两个阶段的弹性模量进行线性化处理，假定这两个阶段的弹性模量均为常数，并建立了双模量理论。1982年Ambartsumyan [1] 发表了关于双模量理论的著作《不同模量弹性理论》，其在该著作中总结了拉压不同模量概念，并提出了拉压不同模量问题的基本假定。经来旺 [2] 在考虑拉压弹性模量不等的条件下推导了弯曲时矩形截面梁弹性力学的解答。结果表明，如果不考虑不同弹性模量将会造成较大的误差。王铭惠、赵永刚等 [3] 基于不同弹性模量理论推导了自由振动时简支梁的应力应变计算公式，并解析了自由振动的前三阶频率和主振型。近年来，国内外诸多学者以不同弹性模量理论为基础研究了各种弹性构件的力学行为 [4] - [13]，但是该理论不够精确。本文研究过程中假定材料的弹性模量与应变的关系是线性的，在此基础上对两端固定铰支梁的弯曲问题进行了研究分析。

2. 基本方程

2.1. 梁的模型

假设梁的长度为l，横截面的高度为h，宽度为b，如图1所示基于几何中面建立笛卡尔坐标系，其上端作用有铅垂均布载荷q。x轴为梁的轴线，y轴为横截面的水平对称轴，z轴为横截面的铅垂对称轴。

2.2. 几何方程

大挠度弯曲变形时，梁几何中面的轴应变 ${\epsilon }_{\text{0}}$ 为：

${\epsilon }_{\text{0}}=\frac{\text{d}u}{\text{d}x}+a\cdot \frac{1}{2}{\left(\frac{\text{d}w}{\text{d}x}\right)}^2$ (1)

其中u为中面轴向位移，w为中面铅垂位移。式(1)中后一项为非线性项，引入参数a，当式(1)中a = 0时为小挠度几何方程，a = 1时为大挠度几何方程。

而任一点上应变 $\epsilon$ 为：

$\epsilon =\frac{\text{d}u}{\text{d}x}-z\cdot \frac{{\text{d}}^{2}w}{\text{d}{x}^2}+a\cdot \frac{1}{2}{\left(\frac{\text{d}w}{\text{d}x}\right)}^2$ (2)

Figure 1. Schematic diagram of beam size and coordinate system

图1. 梁的尺寸和坐标系示意图

2.3. 物理方程

假设弹性模量与应变是线性关系，即：

$E=E\left(\epsilon \right)=E_0+E_1\epsilon =E_0\left(1+E_r\epsilon \right)$ (3)

其中：E₀是材料的初始弹性模量；E₁是弹性模量变化参数； $E_r=\frac{E_1}{E_0}$ 是一个无量纲参数，其反映了本构

关系的非线性程度。

由Hooke定律可知，当承受外力弯曲变形时，梁横截面上的应力与应变的关系为：

$\sigma =E\epsilon =E\left(\epsilon \right)\cdot \epsilon =E_0\left(1+E_r\epsilon \right)\epsilon =E_0\left(\epsilon +E_r{\epsilon }^2\right)$ (4)

若令 $\sigma =0$，并结合式(2)可得梁中性轴的位置表达式：

$z_0=\left[\frac{\text{d}u}{\text{d}x}+a\cdot \frac{1}{2}{\left(\frac{\text{d}w}{\text{d}x}\right)}^2\right]/\frac{{\text{d}}^{2}w}{\text{d}{x}^2}$ (5)

梁的轴力F_N及弯矩M的表达式为：

$\begin{array}{l}{F}_N={\displaystyle {\int }_{-h/2}^{h/2}\sigma \cdot b\text{d}z}=\frac{1}{4}{E}_{0}b\left\{\frac{1}{3}{E}_r{\left(\frac{{\text{d}}^{2}w}{\text{d}{x}^2}\right)}^2{h}^3+\left[E_r{\left(\frac{\text{d}w}{\text{d}x}\right)}^{2}a+2E_r\frac{\text{d}u}{\text{d}x}+2\right]\left[{\left(\frac{\text{d}w}{\text{d}x}\right)}^{2}a+2\frac{\text{d}u}{\text{d}x}\right]h\right\}\\ M={\displaystyle {\int }_{-h/2}^{h/2}-\sigma z\cdot b\text{d}z}=\frac{1}{12}{E}_{0}b\frac{{\text{d}}^{2}w}{\text{d}{x}^2}\left[E_r{\left(\frac{\text{d}w}{\text{d}x}\right)}^{2}a+2E_r\frac{\text{d}u}{\text{d}x}+1\right]h^3\end{array}$ (6)

2.4. 平衡方程

在梁上取微段，研究其平衡并忽略高阶小量，得内力平衡方程：

$\frac{\text{d}{F}_N}{\text{d}x}=0$ (7)

$\frac{{\text{d}}^{2}M}{\text{d}{x}^2}-F_N\frac{{\text{d}}^{2}w}{\text{d}{x}^2}-q=0$ (8)

两端固定铰支边界条件为：

$u=0$, $w=0$, $M=0$ (9)

3. 对基本方程和边界条件进行无量纲处理

为使所求结果具有普遍性且计算方便，特引入如下无量纲参数并对基本方程和边界条件进行无量纲化：

$W=\frac{w}{h}$, $X=\frac{x}{l}$, $U=\frac{ul}{h^2}$, $\delta =\frac{h}{l}$, $Q=\frac{12q}{E_{0}b{\delta }^4}$ (10)

无量纲处理后的内力表达式为：

$\begin{array}{l}\overline{F_N}=\frac{12F_N}{E_{0}bl{\delta }^3}=E_r{\delta }^2{\left(\frac{{\text{d}}^{2}W}{\text{d}{X}^2}\right)}^2+3\left[E_r{\delta }^{2}a{\left(\frac{\text{d}W}{\text{d}X}\right)}^2+2E_r{\delta }^2\frac{\text{d}U}{\text{d}X}+2\right]\left[{\left(\frac{\text{d}W}{\text{d}X}\right)}^{2}a+2\frac{\text{d}U}{\text{d}X}\right]\\ \bar{M}=\frac{12M}{E_{0}b{l}^2{\delta }^4}=\frac{{\text{d}}^{2}W}{\text{d}{X}^2}\left[E_r{\delta }^2{\left(\frac{\text{d}W}{\text{d}X}\right)}^{2}a+2E_r{\delta }^2\frac{\text{d}U}{\text{d}X}+1\right]\end{array}$ (11)

无量纲处理后的平衡方程：

$\frac{\text{d}\overline{F_N}}{\text{d}X}=0$, $\frac{{\text{d}}^2\bar{M}}{\text{d}{X}^2}-Q-\overline{F_N}\frac{{\text{d}}^{2}W}{\text{d}{X}^2}=0$ (12)

无量纲处理后的边界条件为：

固定铰支端：在 $X=0,1$ 时 $U=0$， $W=0$， $\frac{{\text{d}}^{2}W}{\text{d}{X}^2}=0$。

4. 数值求解与结果分析

图2给出了a = 0 (即小挠度)且长细比 $\delta =0.08$，E_r取不同值时，随着载荷Q逐渐增大两端固定铰支梁中点挠度W(0.5)的平衡路径。因为两端固定铰支时梁内轴力不为零，所以当 $E_r=0$ 时中点的挠度W(0.5)与载荷Q成正比关系， $E_r\ne 0$ 时中点挠度与载荷Q的关系不再是线性关系。当 $E_r>0$ 时，其中点挠度曲线在 $E_r=0$ 时中点挠度曲线的下方且在同一载荷下E_r越大中点挠度越小，这说明梁的抗弯能力随着E_r的增大而增加。 $E_r<0$ 时，其挠曲线在 $E_r=0$ 时挠曲线的上方，在同一载荷作用下随着E_r的减小中点挠度增大，这说明梁的抗弯能力随着 $\left|E_r\right|$ 的增大而减小，且当载荷增加到一定程度的时候挠曲线的切线垂直于Q轴，该现象说明此时所取的梁微段不是静力平衡状态，原因是弯曲变形时梁几何中面的拉伸使其横截面上的线应变增加，因而弹性模量减小，弯曲变形越大弹性模量变得越小，当外载荷Q超过极限值时，内力将不足使梁微段达到静力平衡，呈现出软弹簧效应。

图3给出了 $Q=50$， $\delta =0.08$，两端固定铰支且考虑小挠度(即 $a=0$ )时，E_r对梁的弯曲挠度和中性轴位置的影响。可以看出，同一载荷下随着E_r的增大梁各点的挠度相对减小。梁的两端为固定铰支时，其两端截面上不存在弯矩，所以两个端点处不存在弯曲中性层。而 $E_r\ne 0$ 时其他点处中性层位置出现正负交替变换的情况，原因是该边界条件对梁的几何中面轴向变形具有约束，此时梁的横截面上将出现轴向力并会对中性轴位置产生影响，所以梁的中性轴位置Z₀受轴向力和弯矩影响出现正负交替变换的情况，当 $E_r=0$ 时梁内轴向力为零，所以梁的中性轴位置 $Z_0=0$。

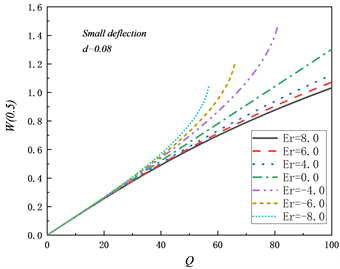
Figure 2. Relationship between beam midpoint deflection W(0.5) and load Q at small deflection

图2. 小挠度时梁中点挠度W(0.5)与载荷Q关系

(a) 弯曲挠度 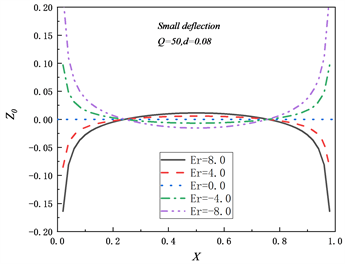(b) 中性轴位置

Figure 3. Bending deflection and neutral axis position of small deflection beam when Q = 50

图3. Q = 50时小挠度梁的弯曲挠度与中性轴位置

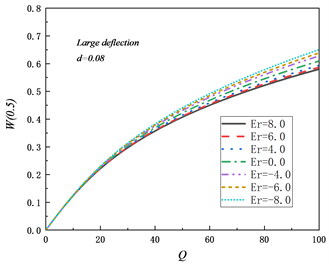(a) 中点挠度W(0.5)与载荷Q关系 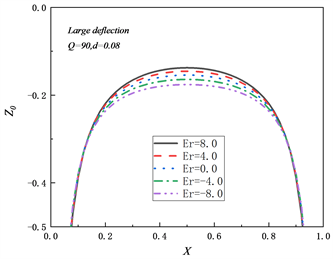(b) 中性轴位置

Figure 4. The relationship between the midpoint deflection W(0.5) of the large deflection beam and the load Q and the position of the neutral axis when Q = 90

图4. 大挠度梁的中点挠度W(0.5)与载荷Q的关系和Q = 90时中性轴位置

图4(a)给出了考虑大挠度(即 $a=1$ )且长细比 $\delta =0.08$，E_r取不同值时，大挠度梁的中点挠度W(0.5)与载荷Q的关系。 $E_r=0$ 时中点挠度与载荷的关系不再是线性变化，这是因为考虑了几何方程中的非线性项。 $E_r\ne 0$ 时平衡路径依旧分布在 $E_r=0$ 时的两侧且 $E_r<0$ 时没有出现软弹簧效应。与图2相比较发现相同E_r且中点挠度较小时，小挠度平衡路径与大挠度平衡路径之间有显著差别。

图4(b)给出了 $Q=90$， $\delta =0.08$ 时大挠度(即 $a=1$ )梁在两端固定铰支情况下中性轴的位置，由于考虑了几何方程中的非线性项，当 $E_r=0$ 时梁内的轴向力不为零，所以中性轴位置Z₀不等于零，且由于轴向拉力的影响，使得中性轴位置均在梁几何中面的下方。

5. 结论

本文在本构关系非线性的基础上，研究了铅垂均布载荷作用下两端固定铰支梁的弯曲问题，假定弹性模量与应变的关系是线性的，然后推导出基本方程并进行无量纲处理，再利用数值法求解梁在该边界条件下的小挠度和大挠度弯曲问题的数值结果并进行分析，结果表明：

1) E_r影响梁的弯曲刚度，且同一载荷下E_r增大时梁的弯曲刚度增大。小挠度情况下E_r取正值和负值时梁的中性层位置相反，大挠度情况下中性层位置在同一侧。

2) 两端固定铰支使梁的几何中面轴向变形受到约束，因而 $E_r\ne 0$ 时梁的横截面产生了轴向力，所以中性层位置改变了且随着E_r的变化而改变。

3) 若研究梁的弯曲问题时考虑了本构关系的非线性，采用大挠度问题的方程求解较为合适。

基金项目

本文得到国家自然科学基金11472123的资助。