基于MOPSO三重移相控制优化研究

doi:10.12677/JEE.2021.91002

期刊菜单

基于MOPSO三重移相控制优化研究
Research on Optimal Control of Triple Phase Shift Angle Based on MOPSO

DOI: 10.12677/JEE.2021.91002, PDF, HTML, XML, 科研立项经费支持
作者: 胡聪卫, 高圣伟：天津工业大学电工电能新技术重点实验室，天津；刘赫, 董晨名：天津金沃能源科技股份有限公司，天津
关键词: 三重移相控制；粒子群算法；双向全桥变换器；Triple Phase Shift (TPS)； Particle Swarm Optimization (PSO)； Dual-Active-Bridge (DAB)

摘要: 三重移相控制双向全桥(Dual-Active-Bridge, DAB) DC/DC变换器功率密度高、工作方式灵活应用非常广泛，但是存在控制量复杂、回流功率高的缺点。本文针对以上缺陷，通过分析三重移相控制策略，进一步分析三自由度对传输功率和电感电流有效值的不同影响，设计了传输功率、电感电流有效值与三重移相控制中三自由度的关系方程；基于该方程，采用智能粒子群算法对移相角进行优化，能够提高最优移相角收敛速度。仿真和实验表明该方法可以实现降低回流功率与降低电感电流有效值的目标。

Abstract: Dual-active-bridge (DAB) DC/DC converter is widely used for its high power density and flexible operation mode. But it also has the disadvantages of complicated control amount and high return power. However, the complexity of control quantity and high reflux power are the main disadvantages of the system, which has become the bottleneck of its development. In view of the above defects, by analyzing the triple-phase-shift (TPS) control strategy, this paper further analyzes the different effects of the three phase-shifting degrees of freedom on the transmission power and the effective values of the inductance current. In this paper, based on the TPS control strategy, the influence of three degrees of freedom on transmission power and effective value of inductor current is analyzed, and the relationship equation between the transmitted power and the effective values of the inductance current in the TPS control system is designed. Based on the equation, intelligent particle swarm optimization (PSO) is used to optimize the phase shift angle. the method that using intelligent PSO to optimize the three phase shift angle has been proposed, which can improve the convergence speed of the optimal phase shift angle. Simulation and experiments show that this method can improve the transmission power and reduce the effective value of inductance current.

文章引用：胡聪卫, 高圣伟, 刘赫, 董晨名. 基于MOPSO三重移相控制优化研究[J]. 电气工程, 2021, 9(1): 11-23. https://doi.org/10.12677/JEE.2021.91002

1. 引言

双主动全桥(Dual Active Bridge, DAB)变换器具有高功率密度，能量双向流动，模块化对称结构等特点，在电力电子变压器、电动汽车、可再生能源发电与储能等场合有着重要应用 [1]。

单移相控制(Single Phase Shift, SPS)是DAB变换器原始的控制方式之一。由于单移相控制没有考虑有功功率传输过程中有一部分能量从输出侧传回输入侧，即回流功率 [2] (或称环流功率或无功功率)。事实上，当采用移相控制时，DAB具有三个互相独立的控制自由度，SPS控制和扩展移相控制(Extended phase shift control, EPS)均是三重移相控制(Triple phase shift control, TPS)的一种特殊情况，因此对TPS控制进行研究更具有一般性和普遍适用性 [3] [4] [5]。

近年来，对于DAB变换器的移相控制策略优化研究成为一大热点。在文献 [6] 中针对线性二次调节器问题运用线性矩阵不等式优化理论，在满足给定的约束条件下，得到了变换器优化参数的求解表达式，完成了闭环控制系统。文献 [7] [8] [9] 均采用双重移相控制 + PWM (脉宽调制)的混合控制策略，实现了所有开关管在全功率范围内实现ZVS，有效减小开关损耗。文献 [10] 提出了满足软开关条件的基于最小回流功率的双重移相控制策略，建立双重移相控制下变换器的动态小信号模型，提高变换器效率。文献 [11] [12] [13] 实现以电流应力为优化目标采用双重移相控制策略，减少暂态过程中电流冲击效应。文献 [14] 提出了一种用于分析移相控制双有源直流变换器的控制特点、功率的传输与交流相量分析方法。对功率范围进行了划分，并提出不同控制策略下的实际控制区域。文献 [15] 采用傅里叶级数求和的方法建立双有源桥DC/DC变换器在移相控制下统一的数学模型，提出了优化电感电流有效值的双重移相控制方式。文献 [16] 通过分析三重移相控制下双主动全桥变换器的等效电路，推导出传输功率及电感电流有效值与控制量之间统一模型，提出针对电感电流有效值的全局优化条件。文献 [17] 则通过将移相控制时三个相互独立的移相自由度任意组合，详细分析DAB系统的12种工作状态。对三个移相自由度做特殊赋值时，改善全桥变换器功率调节范围控制，提高了控制灵活度。综上，对移相控制策略下的DAB变换器的回流功率优化有以下2个方面：1) 改变控制策略，增加控制量，采用双重移相控制、扩展移相控制和三重移相控制扩大传输效率减小回流功率的影响；2) 提高移相控制策略下的数学模型准确性，对不同移相自由度组合、工作模态与不同控制策略下的实际控制区域进行详细分析。由于三个移相自由度之间相互独立，且TPS控制下的DAB具有12种工作模态。对于图1所示的DAB系统，其具有无穷多种开关组合状态，对组合分析过程计算量大，过程繁琐，不能有效快速得出精确的组合结果，因此对TPS控制下出现的所有模式的开关组合进行完全分类是TPS控制的难点。并且在实际工程当中，单一方面的优化并不能满足系统整体效能的提升。

本文首先分析TPS控制原理，推导出三个移相自由度与传输功率，回流功率以及电感电流有效值之间的关系，提出采用多目标粒子群智能算法 [18] 对TPS控制下DAB变换器传输功率及电感电流有效值进行优化控制方法，并对基于不同权重优化目标方法与基于Pareto优化控制方法进行对比，并搭建实验样机结合dSPACE实验平台进行验证。

2. 移相比组合优化分析

2.1. 传输功率特性分析

三重移相控制是在单移相的基础上发展而来，即在变压器二次侧增加内移相角D₂且与一次侧内移相角D₁不相等，在两个全桥之间增加外移相角D₀，范围均为[0, 1]。以功率从左到右传输为例，开关器件S₁~S₄组成全桥逆变电路，S₅~S₈组成全桥整流电路，通过变压器漏电感L及变压器连接，变压器变比为n:1，输入、出端口电压分别为V₁和V₂。

Figure 1. DAB converter topology diagram

图1. DAB的拓扑结构图

TPS与传统控制方式相比，控制灵活度增加，传输功率的范围从曲线扩展成曲面。如图1所示DAB，一次侧全桥的输出电压V_P受控于D₁，二次侧输出电压V_S受控于D₀、D₂。一次侧全桥输出电压V_P跟随D₁的变化，输出电压V_P波形呈现出“0正0负”的变化规律。二次侧全桥输出电压V_s则随着D₀、D₂的变化而变化，具体来说可能有四种变化规律，即“0正0负”、“0负0正”、“正0负0”、“负0正0”。即在三重移相控制下由于增加桥间移相角，变压器原副边电压形成三电平方波。为简化数学模型，根据以上的变化规律，如图2所示，可将产生的三电平方波可以分解成两个对称的两电平方波。则一次侧全桥输出电压、二次侧全桥输出电压可表示为式(1)。

${\begin{cases} v_{p} (t) = V_{1} (S (t) + S (t - D_{1} T)) \\ v_{s} (t) = V_{2} (S (t - D_{0} T) + S (t - D_{0} T - D_{2} T)) \end{cases}$ (1)

Figure 2. DAB equivalent transformation model

图2. DAB等效变换模型

其中，在图3中，S(t)表示标准的两电平方波。

Figure 3. Standard two-level waveform

图3. 标准两电平波形

根据DAB变换器电路可得电感电流值与变压器原副边电压关系如下：

$L \frac{d i_{L}}{d t} = v_{p} - n v_{s} = V_{1} (S (t) + S (t - D_{1} T)) - n V_{2} S (t - D_{0} T) + S (t - D_{0} T - D_{2} T)$ (2)

则式(2)可变形为：

$i_{L} (t) = \frac{\int [V_{1} (S (t) + S (t - D_{1} T))] d t}{L} - \frac{\int [n V_{2} (S (t - D_{0} T) + S (t - D_{1} T))] d t}{L}$ (3)

由式(1)和式(3)可得出传输功率为：

$P = v_{p} (t) \int i_{L} (t) d t$ (4)

由式(4)可得传输功率可表示为：

$P = - \frac{n V_{1} V_{2}}{T L} \int_{D_{1} T}^{T} (\int_{D_{1} T}^{T} (S (t - D_{0} T) + S (t - D_{0} T - D_{2} T)) d t) d t$ (5)

同理，可得电感电流有效值为：

$I_{r m s}^{2} = \frac{1}{T} \int_{0}^{T} i^{2} (t) d t = \frac{1}{T L^{2}} \int_{0}^{T} (\int_{0}^{T} (V_{1} (S (t) + S (t - D_{1} T)) - n V_{2} (S (t - D_{0} T) + S (t - D_{1} T))) d t) d t$ (6)

因此，在三重移相控制下，因控制量的增加，调节参量的范围不同，则存在十二种功率传输模式。且三个控制量相互独立，传输功率与电感电流有效值均是关于D₀、D₁、D₂的函数。根据功率传输范围，正向传输过程六种功率传输模式，如图4所示。根据功率传输方向分为六种正向传输模式和六种反向传输模式。因DAB变换器结构的对称性，一般只研究功率正向传输，且在正向传输的六种传输模式的范围如下表1所示。

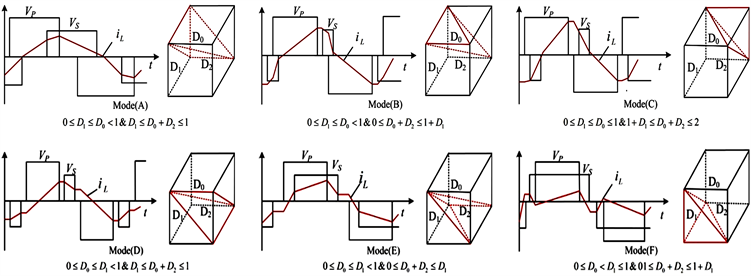
Figure 4. Main voltage and current waveforms in six working modes

图4. 六种工作模式主要电压电流波形

Table 1. Six power transmission mode ranges

表1. 六种功率传输模式范围

由结合表1和图4可知，DAB变换器在模式A下可以达到最大传输功率，模式C、D均可以进行能量反向传输。但模式C、D和B下，不存在 $V_{P} (t) \cdot V_{s} (t) > 0$ 时间段，能量不能通过输入端口直接向输出端口传递，需通过电感储存能量，使电感电流急剧增加，因此会造成额外回流功率。根据TPS控制下传输功率范围及一次侧全桥输出电压V_P、二次侧全桥输出电压V_S的组合规律，可以得出所研究3种模式下三个移相角值范围与电压电感主要波形。且可以推导出A、E、F三种模式下传输功率公式如下：

${\begin{cases} P_{A} = \frac{- V_{1} V_{2} T}{L} (- D_{0} + D_{0}^{2} + 0.5 D_{1} - D_{0} D_{1} + 0.5 D_{2} + D_{0} D_{2} + 0.5 D_{2}^{2}) \\ P_{E} = \frac{- V_{1} V_{2} T}{L} (- D_{0} + 0.5 D_{1} + D_{0} D_{1} - 0.5 D_{1}^{2} - 0.5 D_{2} + 0.5 D_{1} D_{2}) \\ P_{F} = \frac{- V_{1} V_{2} T}{L} (- D_{0} + 0.5 D_{0}^{2} + 0.5 D_{1} - 0.5 D_{2} + D_{0} D_{2} - 0.5 D_{1} D_{2} + 0.5 D_{2}^{2}) \end{cases}$ (7)

为了运算简便，取单移相传输功率最大值为基准值对所得到的三种模式下传输功率标幺值化。

$\bar{P} = \frac{P}{\frac{n V_{1} V_{2}}{8 f_{s} L}}$ (8)

由于传输功率与三个移相自由度有关，将外移相角D₂作为可变已知参数选取几组典型的P关于D₀、D₁的三维曲线。对于模式A，当D₂ = 0时，TPS控制依旧可以传输功率且随着D₂的增大，传输范围越来越小，如图5所示。

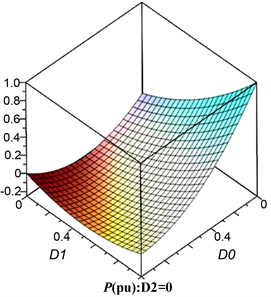
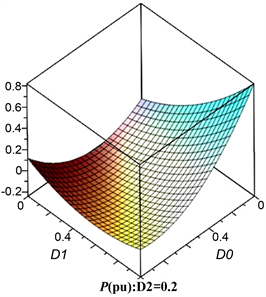
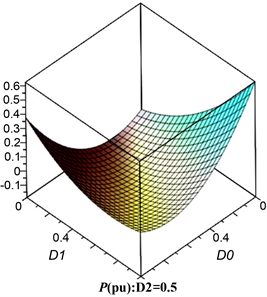
Figure 5. Three-dimensional change graph of sub-mode standardized transmission power

图5. 子模态标准化传输功率的三维变化图

由此可以看出对于一个TPS控制下DAB系统，三个移相比的选择至关重要，并且可以有多种移相自由度组合情况而影响传输功率的范围，但这也为系统的优化提供可能。

2.2. 回流功率特性分析

从数理的角度分析，结合回流功率的数学模型，对不同模式下电感电流和其电压波形可得出，回流功率的产生始终取决于原边电压和电感电流以及电感电流过零的时刻。如图6所示，TPS控制下回流功率如阴影部分所示。根据对不同模式下电感电流和其电压波形可得出：在D₁T时间范围内产生回流功率(无功功率)且无功功率的大小取决于电感电流为0时刻。

当 $t_{z e r o} \leq \frac{1}{2} (1 - D_{1}) T$ 时，回流功率小于等于0。回流功率可表示为：

$P_{c i r} = | - v_{p} (t) \int i_{L} (t) d t |$ (9)

Figure 6. Schematic diagram of sub-modal return power

图6. 子模态回流功率示意图

故取 $t_{z e r o} = \frac{1}{2} (1 - D_{1}) T$ ，由式(1)、(2)和(10)计算可得q且小于等于P_cir。

$q = - (\frac{3}{8} D_{1}^{2} - \frac{1}{4} D_{1} - \frac{1}{8}) T^{2} V_{1}^{2} + (\frac{1}{2} D_{0} D_{1} - \frac{1}{2} D_{0} + \frac{3}{4} D_{1} D_{2} - \frac{1}{2} D_{1} + \frac{1}{4} D_{2} - \frac{3}{8} D_{1}^{2} - \frac{1}{8}) T^{2} n V_{2} V_{1}$ (10)

为了方便分析，对q进行求导有：

$Δ q = q (D + Δ d) - q (D) \approx \frac{d q}{d D} Δ d = \frac{\partial q}{\partial D_{0}} Δ d_{0} + \frac{\partial q}{\partial D_{1}} Δ d_{1} + \frac{\partial q}{\partial D_{2}} Δ d_{2}$ (11)

由式(11)可得出每一个移相比分别对回流功率的函数关系，如式(12)所示：

${\begin{cases} \frac{\partial q}{\partial D_{0}} = \frac{1}{2} (D_{1} - 1) < 0 \\ \frac{\partial q}{\partial D_{1}} = - (\frac{3}{4} D_{1} - \frac{1}{4}) T^{2} V_{1}^{2} + (\frac{1}{2} D_{0} - \frac{1}{2}) T^{2} n V_{1} V_{2} < 0 \\ \frac{\partial q}{\partial D_{2}} = (\frac{3}{4} D_{1} + \frac{1}{4}) T^{2} n V_{1} V_{2} > 0 \end{cases}$ (12)

所以由此可得D₀、D₁是关于q减函数即是关于P_cir的减函数；D₂是关于P_cir的增函数，D₂越小P_cir越小。当回流功率增大时，传输功率减小，故当增大D₂使会使传输功率减小。因此，若使变换器减小传输过程中的损耗，提高变换器效率，应使桥间移相角D₂尽量小。

2.3. 电感电流有效值特性分析

电流有效值是一个周期内电流的方均根值，主要表征的是变换器的热效应，此对其分析中主要考虑变换器控制稳定运行时的情况即可。为减小TPS控制下回流功率，提高DAB传输功率。其中减小电感电流有效值是一个减少功率损耗的直观方法。可得电感电流有效值为：

$I_{r m s} = \sqrt{\frac{1}{T} \int_{0}^{T} {(i_{L} (t))}^{2} d t}$ (13)

$I_{r m s}^{2} = \frac{1}{T} \int_{0}^{T} i^{2} (t) d t = \frac{1}{T L^{2}} \int_{0}^{T} (\int_{0}^{T} (V_{1} (S (t) + S (t - D_{1} T)) - n V_{2} (S (t - D_{0} T) + S (t - D_{1} T))) d t) d t$ (14)

由电感电流的对称性可知，电感平均电流在一个周期内稳态为0，令D₁ = 0，D₀ = D可得移相控制下t₀与t₁时刻电感电流：

${\begin{cases} i_{L} (t_{0}) = - \frac{n V_{2}}{4 f L} (k + 2 D - 1) \\ i_{L} (t_{1}) = \frac{n V_{2}}{4 f L} (k (2 D - 1) + 1) \end{cases}$ (15)

可得三重移相控制下三种模式A、E、F下电感电流有效值表达式如下：

$\begin{matrix} I_{R M S_{-} A}^{2} = \frac{T^{2}}{L^{2}} (\frac{0.125}{3} V_{1}^{2} + \frac{0.125}{3} V_{2}^{2} + \frac{0.5}{3} (0.25 - 1.5 D_{1}^{2} + D_{1}^{3}) V_{1}^{2} - \frac{0.5}{3} (0.25 - 1.5 D_{0}^{2} + D_{0}^{3}) V_{1} V_{2} \\ - \frac{0.5}{3} (0.25 - 1.5 {(D_{0} - D_{1})}^{2} + {(D_{0} - D_{1})}^{3} V_{1} V_{2}) - \frac{0.5}{3} (0.25 - 1.5 {(D_{0} + D_{2})}^{2} + {(D_{0} + D_{2})}^{3} V_{1} V_{2}) \\ - \frac{0.5}{3} (0.25 - 1.5 {(D_{0} + D_{2} - D_{1})}^{2} + {(D_{0} + D_{2} - D_{1})}^{3} V_{1} V_{2}) + \frac{0.5}{3} (0.25 - 1.5 D_{2}^{2} + D_{2}^{3}) V_{2}^{2}) \end{matrix}$ (16)

$\begin{matrix} I_{R M S_{-} E}^{2} = \frac{T^{2}}{L^{2}} (\frac{0.125}{3} V_{1}^{2} + \frac{0.125}{3} V_{2}^{2} + \frac{0.5}{3} (0.25 - 1.5 D_{1}^{2} + D_{1}^{3}) V_{1}^{2} - \frac{0.5}{3} (0.25 - 1.5 D_{0}^{2} + D_{0}^{3}) V_{1} V_{2} \\ - \frac{0.5}{3} (0.25 - 1.5 {(D_{1} - D_{0})}^{2} + {(D_{1} - D_{0})}^{3} V_{1} V_{2}) - \frac{0.5}{3} (0.25 - 1.5 {(D_{0} + D_{2})}^{2} + {(D_{0} + D_{2})}^{3} V_{1} V_{2}) \\ - \frac{0.5}{3} (0.25 - 1.5 {(D_{1} - D_{2} - D_{0})}^{2} + {(D_{1} - D_{0} - D_{2})}^{3} V_{1} V_{2}) + \frac{0.5}{3} (0.25 - 1.5 D_{2}^{2} + D_{2}^{3}) V_{2}^{2}) \end{matrix}$ (17)

$\begin{matrix} I_{R M S_{-} F}^{2} = \frac{T^{2}}{L^{2}} (\frac{0.125}{3} V_{1}^{2} + \frac{0.125}{3} V_{2}^{2} + \frac{0.5}{3} (0.25 - 1.5 D_{1}^{2} + D_{1}^{3}) V_{1}^{2} - \frac{0.5}{3} (0.25 - 1.5 D_{0}^{2} + D_{0}^{3}) V_{1} V_{2} \\ - \frac{0.5}{3} (0.25 - 1.5 {(D_{1} - D_{0})}^{2} + {(D_{1} - D_{0})}^{3} V_{1} V_{2}) - \frac{0.5}{3} (0.25 - 1.5 {(D_{0} + D_{2})}^{2} + {(D_{0} + D_{2})}^{3} V_{1} V_{2}) \\ - \frac{0.5}{3} (0.25 - 1.5 {(D_{0} + D_{2} - D_{1})}^{2} + {(D_{0} + D_{2} - D_{1})}^{3} V_{1} V_{2}) + \frac{0.5}{3} (0.25 - 1.5 D_{2}^{2} + D_{2}^{3}) V_{2}^{2}) \end{matrix}$ (18)

为了运算简便，可以将电感电流有效值I_rms进行标幺化。其中I_rms所引起的损耗与 $I_{r m s}^{2}$ 成正比，因此I_rms和 $I_{r m s}^{2}$ 单调性相同，直接对 $I_{r m s}^{2}$ 进行处理可以减少运算，所以对 $I_{r m s}^{2}$ 作标幺化处理。

${\bar{I}}_{r m s}^{2} = \frac{I_{r m s}^{2}}{\frac{V_{1}^{2}}{24 f_{s}^{2} L^{2}}}$ (19)

根据上文可得出三种模式下电感电流有效值。电感电流有效值是一个周期内电流的方均根值，表征变换器的热效应。在正向传输的三种模式下，为了方便分析，对三种模式下电感电流有效值分别进行对D₀、D₁、D₂求偏导发现，无法分离三个控制量对电感电流有效值的影响。在此情况下，根据D₂是关于回流功率的增函数，D₂的取值应尽量小。因此将外移相角D₂作为可变已知参数选取几组典型的 $I_{r m s}^{2}$ 关于D₀、D₁的三维曲线。

根据图7可以得出，在D₂从0到0.5过程中电感电流有效值变化。在三种模式的情况下，随着D₂增加，电感电流有效值范围明显变大，若要降低变换器的通态损耗，需降低电感电流有效值，则需移相比D₂在设置时在可行域内取较小值。

由以上对传输功率、回流功率以及电感电流有效值的分析，可以得出P、P_cir和 $I_{r m s}^{2}$ 均是三个移相自由度(D₁、D₂、D₃)的函数，均是四维关系。且因不同的移相自由度组合，传输功率可分为十二种工作模式，具有不同的功率传输范围，为TPS控制下DAB系统优化提供可能。因此本文对功率正向传输当中的A、E、F三种模式进行分析，对四维关系解耦分析，回流功率是关于外移相角D₂的增函数，即D₂越大，回流功率越大，这为电感电流有效值分析提供突破点，因此以外移相角D₂作为可变已知参数，分析D₂对电感电流有效值的影响，在三种模式下，随着D₂增加，电感电流有效值范围明显变大。因此，本文将回流功率与电感电流有效值共同作为优化目标，以三个移相自由度D₁、D₂、D₃作为优化变量采用多目标粒子群算法进行优化。

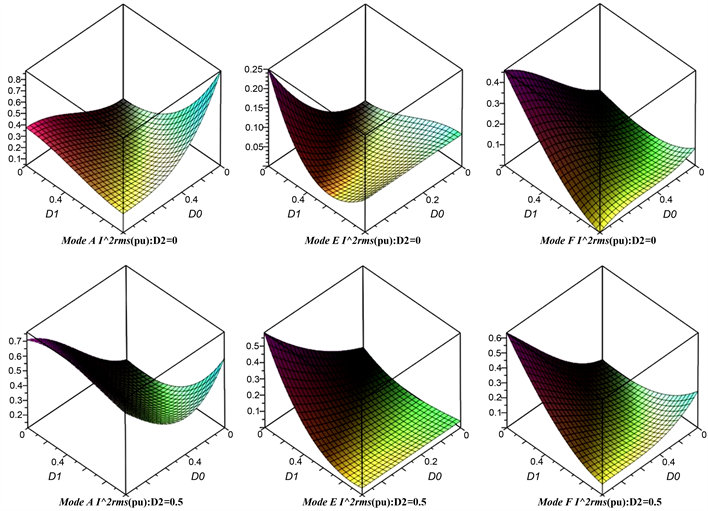
Figure 7. The change of the effective value of the inductor current in the three modes

图7. 三种模式下电感电流有效值的变化图

3. 粒子群优化算法

本文将传输功率和电感电流有效值同时进行优化，是多目标寻优。智能粒子群优化(Particle Swarm Optimization, PSO)算法以其实现容易，精度高，收敛快等优点广受关注。通过模仿鸟群觅食的行为，通过迭代寻优找最优解。粒子群优化算法中，每个优化问题的解都是搜索空间中的一只鸟，被抽象为没有质量和体积的粒子，并将其延伸到N维空间。粒子在该空间中的位置和飞行速度均为矢量。粒子们在飞行过程中发现的最好位置(pbest)和现在的位置都认为是单个粒子的飞行经验。所以粒子发现的最好位置经过比较得出最好的位置，也就是整个种群中最好位置(gbest)，粒子根据如下公式来更新自己的速度和新的位置。

$v_{i, j} (m + 1) = ω v_{i, j} (m) + c_{1} r_{1} (p b e s t_{ι, j} (m) - x_{ι, j} (m)) + c_{2} r_{2} (g b e s t_{ι, j} (m) - x_{ι, j} (m))$ (20)

$x_{i, j} (m + 1) = x_{i, j} (m) + v_{i, j} (m + 1)$ (21)

其中j表示n维空间中的第j维，m表示粒子群到第m个的迭代，ω是粒子惯性，c₁是认知加速常数，c₂是社会加速常数，并且r₁和r₂是0和1之间的随机数。在迭代的早期阶段，算法需要具有强大的全球搜索能力，以防止早产。在迭代的后期阶段，更详细的搜索是需要加速收敛。使用时变惯性权重因子如下：

$ω = (ω_{\max} - ω_{\min}) \frac{M - m}{M} + ω_{\min}$ (22)

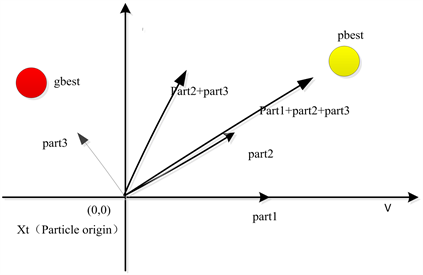
Figure 8. Schematic diagram of space particle position change update

图8. 空间粒子位置变化更新示意图

在图8中，通过减小TPS控制下回流功率来提高DAB传输功率，其中减小电感电流的RMS值是一个减少功率损耗的直观方法。目标函数和约束都是非线性的，传统的方法依赖于梯度信息或拉格朗日乘数理论不是很好适合这个问题。因此，PSO算法用于分析和解决这些问题可以得到TPS控制的三个最佳参数。为了简化PSO的操作，优化问题可以进行简化。式(23)中的通过为每个优化目标添加权重，多目标可以简化为单一目标。最终的优化问题被表述为如下：

$f i t n e s s = λ \cdot {\bar{P}}_{c i r} + (1 - λ) \cdot {\bar{I}}_{r m s}^{2}$ (23)

Figure 9. Combination optimization of f-phase shift based on different weight coefficients

图9. 基于不同权重系数下f移相组合优化

由图9可得对三种模式下不同权重优化结果，虽然有较好的优化结果，但是还是存在比较差的情况，且两个目标之间没有共同的度量标准，很难评判出较好的优化结果。基于不同权重系数的多目标优化因是将两个优化目标转化为单目标优化，只能的到一个最优解，但在实际决策中可能需要多种可供选择的方案。针对以上缺陷，进行进一步优化研究。

${\begin{cases} {\begin{cases} \min [{\bar{P}}_{c i r (A)}, {\bar{I}}_{r m s (A)}^{2}] \\ 0 < D_{1} < D_{0} < 1 & D_{1} < D_{0} + D_{2} < 1 \end{cases} \\ {\begin{cases} \min [{\bar{P}}_{c i r (E)}, {\bar{I}}_{r m s (E)}^{2}] \\ 0 < D_{0} < D_{1} < 1 & 0 < D_{0} + D_{2} < D_{1} \end{cases} \\ {\begin{cases} \min [{\bar{P}}_{c i r (F)}, {\bar{I}}_{r m s (F)}^{2}] \\ 0 < D_{0} < D_{1} < 1 & D_{1} < D_{0} + D_{2} < 1 \end{cases} \end{cases}$ (24)

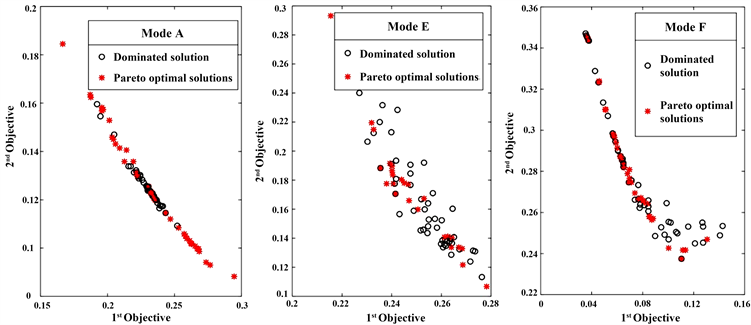
Figure 10. Multi-objective optimization based on Pareto

图10. 基于Pareto多目标移相比组合优化

通过仿真实验表明，在优化控制下，能够明显提高变换器效率，说明优化控制算法的优越性。图9与图10是DAB变换器在以回流功率与电感电流有效值同时作为优化目标的情况。基于Pareto多目标优化有效解决了基于权重方法的缺陷，对于采用Pareto算法优化结果明显好于基于不同权重系数优化结果，且在基于MOPSO多目标优化控制下，变换器效率大幅提高，且比较平坦，说明控制算法具有很好地适应性。

为了对上述理论分析结果进行验证，搭建了如图11、图12所示的DAB实验平台和MOPSO控制器。图11主要是控制部分，通过采集输入电压与输出电压反馈给上位机中MOPSO控制程序，MOPSO算法程序运行输出三个移相自由度，产生PWM信号对DAB变换器进行控制。

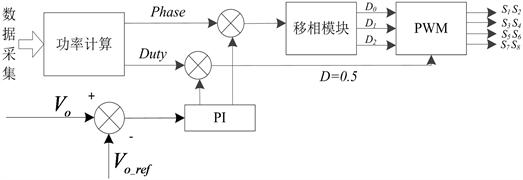
Figure 11. Block diagram of DAB converter optimization control realization

图11. DAB变换器优化控制实现框图

该实验平台采用dSPACE系统、上位机组成控制部分；电子负载可以方便地实现负载变换；DAB部分由两个全桥通过高频隔离变压器和辅助电感组成。分别对于以上两种多目标控制算法进行验证。DAB变换器开关频率为20 kHz，输入输出电压为200 V。

Figure 12. Based on hardware-in-the-loop simulation experiment platform system

图12. 基于半实物仿真实验平台系统

由图13可知，基于不同权重系数目标优化效果逊于Pareto多目标算法。Pareto多目标算法更能适应非线性系统的性能优化。能有效减小变换器轻载时损耗较大，效率较低的问题。

Figure 13. Comparison results of two optimization methods

图13. 两种优化方法对比结果

4. 实验结论

本文针对TPS控制下DAB变换器，通过对变压器一次侧、二次侧电压解耦分析，得到了TPS控制下DAB变换器运行过程中三种不同的工作模态下的三个移相角度与传输功率、回流功率和电感电流有效值的表达式。为同时降低系统中回流功率与电感电流有效值，设计了基于不同权重目标优化和多目标优化控制优化控制器。最后实验结果表明，采用MOPSO算法，能够快速准确得出移相角组合，节省大量时间，对于非线性问题的求解更具有适应性。并且能够有效降低回流功率与电感电流有效值，大幅度提高DAB变换器效率，验证理论结果的有效性。

基金项目

本文的研究工作得到了天津市科技计划项目“高性能光伏储能双向DC-DC变换器研究”(20YDTPJC01520)的支持。

参考文献

[1]	周路遥. 双有源全桥双向DC-DC变换器典型拓扑研究[D]: [硕士学位论文]. 北京: 北京交通大学, 2016.
[2]	冯子秋, 迟颂. 双向全桥DC/DC变换器移相优化的扩展双重移相控制[J]. 电气传动, 2019, 49(7): 25-31.
[3]	未红旗, 周剑君, 祁良甫. 基于TPS的双向全桥DC/DC最小回流功率控制[J]. 电力电子技术, 2017, 51(10): 14-16.
[4]	沙广林. 电力电子变压器中双有源桥DC-DC变换器的研究[D]: [博士学位论文]. 北京: 中国矿业大学(北京), 2016.
[5]	武琳, 刘志刚, 洪祥. 隔离式双向全桥DC-DC变换器的功率控制特性比较与分析[J]. 电工技术学报, 2013, 28(10): 179-187.
[6]	柳杨. 隔离型双向全桥DC/DC变换器优化控制研究[D]: [硕士学位论文]. 重庆: 重庆大学, 2015.
[7]	李良光, 李文君, 朱孟江. UPS双重移相控制的双有源桥DC/DC变换器研究[J]. 电力电子技术, 2019, 53(6): 111-114.
[8]	孙孝峰, 吴晓颖, 申彦峰, 崔明勇, 李昕. 一种全功率范围零电压开通的电流型双向隔离DC-DC变换器[J]. 电工技术学报, 2018, 33(10): 2282-2292.
[9]	吴俊娟, 孟德越, 申彦峰, 沈虹, 孙孝峰. 双重移相控制与传统移相控制相结合的双有源桥式DC-DC变换器优化控制策略[J]. 电工技术学报, 2016, 31(19): 97-105.
[10]	程红, 高巧梅, 朱锦标, 杨小康, 王聪. 基于双重移相控制的双向全桥DC-DC变换器动态建模与最小回流功率控制[J]. 电工技术学报, 2014, 29(3): 245-253.
[11]	安峰, 杨柯欣, 王嵩, 罗书聪, 冯晓云. 基于模型前馈的双有源全桥DC-DC变换器电流应力优化方法[J]. 电工技术学报, 2019, 34(14): 2946-2956.
[12]	曾进辉, 孙志峰, 雷敏, 兰征. 双重移相控制的双主动全桥变换器全局电流应力分析及优化控制策略[J]. 电工技术学报, 2019, 34(12): 2507-2518.
[13]	黄珺, 王跃, 李卓强, 雷万钧. 基于三重移相控制的双主动全桥直流变换器优化调制策略[J]. 中国电机工程学报, 2016, 36(6): 1658-1666.
[14]	沙广林, 王聪, 程红, 邓嘉卿, 王健宇. 移相控制的双有源桥DC-DC变换器统一相量分析法[J]. 电工技术学报, 2017, 32(18): 175-185.
[15]	程红, 马志鹏, 王聪, 沙广林. 基于傅里叶级数建模的双有源桥DC-DC变换器电流有效值分析[J]. 电力自动化设备, 2017, 37(5): 14-20.
[16]	童安平, 杭丽君, 李国杰. 三重移相控制下DAB变换器全局优化控制策略及分析[J]. 中国电机工程学报, 2017, 37(20): 6037-6049.
[17]	谷庆, 袁立强, 聂金铜, 李婧, 赵争鸣. 基于开关组合规律的双有源桥DC-DC变换器传输功率特性[J]. 电工技术学报, 2017, 32(13): 69-79.
[18]	王凯丽, 张巧杰. MOPSO算法在Boost变换器优化设计中的应用[J]. 烟台大学学报(自然科学与工程版), 2017, 30(4): 317-322.

友情链接