1. 引言
柔性体与流体的耦合运动(Fluid-Flexible-Structure-Interaction)现象广泛的存在于各学科领域和工程实际中。如在仿生学中,通过对飞行和游动生物的深入观测研究,研制出的微型飞行器和水下航行器等高精器械大量的用于航天航空和国防事业之中 [1] [2] [3] [4] [5],其中生物的飞行和游动本质上是柔性体(翅膀、尾鳍)和流体(气流、水流)的耦合运动。在生物医学上,血液的流动、人工心脏瓣膜的开合以及打鼾等现象亦都涉及到柔性体(血管、心脏瓣膜和软腭)与流体(血液和气流)的耦合运动 [6] [7] [8] [9]。另外,在纸张、丝绸以及塑料薄膜等物品与材料的生产制造过程中,应充分考虑这些柔性材料与气流相互作用产生的耦合运动,避免因气流引起的大幅度摆动而造成的破坏 [10]。在高压输电线路和海底电缆、管道等工程项目的设计和实施中,亦应充分考虑柔性体(输电线、电缆、管道)与流体(风载、水流)之间相互作用产生的耦合运动所带来的影响 [11]。因在现实生活中,材料的均匀性是抽象化、理想化的。故在上述学科领域和工程实际中所描述的柔性体,相较于均匀柔性体,非均匀柔性体更贴合实际以及更具有代表性。因此,变截面柔性体与流体的耦合运动特性研究在国防安全、医疗健康和基础建设等方面具有重要的应用价值且亟待开展。
柔性体与流体的耦合运动属于流固耦合(Fluid-Structure-Interaction)范畴。由于流固耦合问题涉及多领域,且具有多场耦合、多重非线性等复杂特征,难以给出精确的解答,所以对该问题的研究以实验和数值模拟的方法为主。在最初该问题的研究中通常采用一个位于轴向流中前边缘固定后边缘自由的悬臂柔性板的经典模型 [12],如Taneda的第一次试验在一个垂直风洞中利用该模型对不同材质(丝绸、帆布、薄纱)和形状(矩形、三角形)的旗帜进行了详细的实验 [13]。Datta和Gottenberg进行了类似的实验,并研究了临界流速与柔性体长度和厚度之间的关系 [14];紧接着Lemaitre、Yamaguchi等人对不同高宽比的柔性材料做了详细的实验研究 [15] [16]。在这些实验结果中系统地发现临界速度高于理论预测值 [17],这种差异的根源与一直以来的平面假设有关 [18]。在最近的柔性体与流体的耦合运动研究中,孙传宝和王思莹等人分别做了一个和两个柔性旗帜在均匀流中的摆动实验 [19] [20],Kim等人做了一个前边缘自由后边缘固定的反向悬臂柔性体的实验,研究了自由边缘涡旋的形成与柔性体的弹性应变能之间的关系 [21]。Jia等人采用线性梁模型解析的给出了柔性体的频率和波数与风速之间的尺度律 [12]。Cisonni等人研究了二维粘性流中柔性体的非均匀部分对整体运动的影响 [22]。在上述的研究中,由于柔性体抗弯刚度较小的特性,其在与流体相互作用时一般会发生较大变形,因此对于这类流固耦合问题给出解析解是比较困难的 。本文将在均匀柔性体的基础上,解析地给出非均匀柔性体与气流的耦合运动特性。
柔性体与流体的耦合运动特性研究不仅可以使我们了解“鹰击长空,鱼翔浅底”等美丽场景背后的奥妙,更能使我们精确的掌握流固耦合现象的内在机理。这对于涉及风载、水流等流体的构件或机械的设计和制造有着指导性作用。本文通过Euler-Bernoulli梁假设和理想流体假设对气流中两端夹紧变截面柔性杆的运动做了深入研究,给出了该变截面柔性杆与流体耦合运动时的波扰动时间增长率和特征函数的表达式,并讨论了角频率与扰动时间增长率的变化规律,为非均匀柔性杆与流体耦合运动的相关实验研究和数值模拟提供了理论依据。
2. 控制方程
将一个无限长的变截面柔性杆置于轴向气流流速为V的风场中,如图1所示。
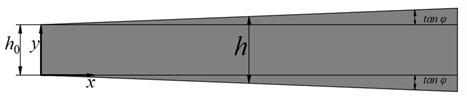 (a) 变截面柔性杆(Flexible rod with variable cross-section)
(a) 变截面柔性杆(Flexible rod with variable cross-section) (b) 运动模型(Motion model)
(b) 运动模型(Motion model)
Figure 1. Model of interaction between airflow and flexible rod with variable cross-section
图1. 变截面柔性杆与气流耦合运动模型
其中
分别为横纵坐标且均以固定端A为起点,A、B分别为柔性杆两端在风场中的固定位置;
和E分别为柔性杆的挠度和弹性模量。柔性杆某一横向位置处的直径为
(令
),其中
和
分别为该柔性杆的初始直径和截面变化系数。假设柔性杆两个固定端(A、B)之间的部分足够长(忽略固定端对柔性杆运动的影响),风速恒定且在柔性杆两侧均匀流动。对于固定端之间的柔性杆本文将其看作经典梁(Euler-Bernoulli beam)来处理,则由经典梁的动力学平衡方程 [23] 可得该变截面柔性杆与气流耦合运动时的平衡方程:
(1)
其中,
,
,
,
是柔性体的密度,
是柔性体两侧的压强差。
忽略气流粘性并假设其不可压缩(气流流速较小,马赫数小于0.3时,可以将气流视作不可压缩流体 [24] ),则此时流场的连续方程和动量方程为:
(2)
(3)
其中
为气流密度,
和p分别为流速和压强。
由于柔性杆的不可渗透性,故当柔性杆与气流发生耦合运动时,柔性杆的速度应等于柔性杆上气流流速,则有:
(4)
其中
是柔性杆的法向量。
3. 线性稳定性分析
因方程(1)是根据线性梁理论得出的平衡方程,又方程(2)~(4)和方程(1)因耦合关系共同构成闭合方程组,所以对方程(1)~(4)应进行一致的线性化处理才能对其求解。本文假设变截面柔性杆两固定端之间的部分足够长,可以忽略固定端边界条件对耦合运动的影响,并假设变截面柔性杆在气流作用下,两固定端之间部分的运动模态是以
为频率的正弦形式(
为柔性杆运动时的频率,
为波扰动时间增长率)。则有:
(5)
(6)
(7)
(8)
其中
为柔性杆的挠曲线方程,A和k分别为柔性杆挠曲线的振幅和波数;V为风场中气流的平均流速,
为扰动波沿着y方向的空间衰减率;
和
分别为柔性杆运动时气流在x和y方向上的流速,p为柔性杆运动时流场内的压强;U、W、
分别是定义的无量纲未知量。上述四个量
、
、
和p的线性化处理均是将其写作零阶项和一阶项的和,其中每个量的零阶项对应于柔性杆未发生运动(扰动)时该量的初始值,一阶项对应于柔性杆发生运动(扰动)后,柔性杆的运动对该量的“影响值”。例如在
的线性化处理中,零阶项是初始气流流速V,一阶项是由柔性杆运动(扰动)引起的横向速度的变化量;类似的,可得到另外三个量
、
和p的表达式。在柔性杆与流体耦合运动的实验中,表达式(5)~(8)中的未知量仅为U、W、
和
,其他量均可由实验测得 [12],这里本文仅做理论推导。
将(5)~(8)带入到(1)~(4)中,求解未知量得:
(9)
(10)
(11)
(12)
在表达式(9)中,因柔性杆的运动对流场的影响在远离柔性杆的方向上愈来愈弱,故本文设定:在
的区域有
,反之则为
,其中
符号对应着y的正负区域。由表达式(12)可得柔性杆两侧压强差
为:
(13)
将表达式(5)和(13)带入方程(1),则有:
(14)
4. 色散关系
将柔性杆直径
带入方程(14)中,并引入如下无量纲变量将其无量纲化:
,
,
,
,
.
得到关于
的无量纲方程:
(15)
由于对柔性体研究一般所选取的研究对象为薄片状或细长杆状柔性材料 [25] [26],又为了符合柔性体波动的实际情况,故本文所取的变截面柔性杆的截面变化系数
是一个非常小的值(
)。在方程(15)的第一项中,因
项不包含截面变化系数
,其值远远大于另外两项,所以可以略去
项和
项,有:
(16)
显然,(16)式是一个关于
的二次方程,解该方程得:
(17)
在式(17)的平方根表达式中可以定义一个截至波数
,为:
(18)
其中
是变截面柔性杆与气流耦合运动时,波动趋于稳定的临界波数。根据式(18)可求得
,其中
为
,
,
和
的函数。当波数大于
时(求解出具体的
后,可判断波数大于或小于
时扰动时间增长率
是否存在,具体见图3),由频率
的表达式可知,
,此时的频率是一个实数;即此时柔性杆的运动趋于稳定—波形既不增长也不扩散。当波数小于
时,
,此时频率为复数,由复频率
可得此时角频率和扰动时间增长率的表达式为:
(19)
(20)
由式(19)可得无量纲角频率
与无量纲波数
的关系曲线图(对于具体的单个柔性体,材料密度为定值,本文给定其值为
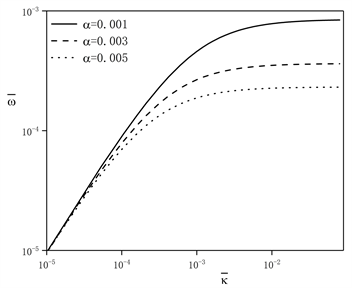
),如图2所示:
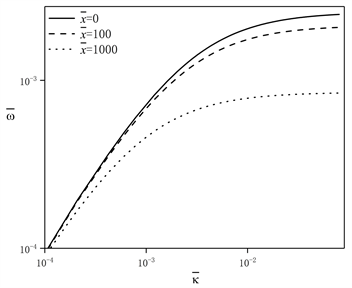
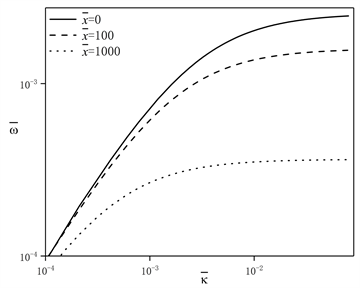
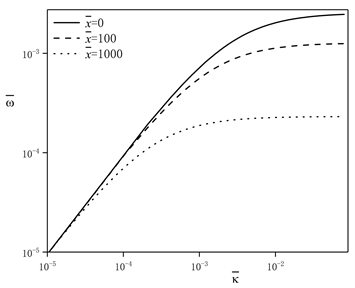
(a) (
) (b) (
)(c) (
) (d) (
)
Figure 2. The effect of dimensionless wave number on dimensionless angular frequency with respectively different the cross-section change coefficient and the transverse position
图2. 截面变化系数和横向位置分别不同时,无量纲波数对无量纲角频率的影响
由图2中,a~c图可知,当波数在不稳定范围内(
)且横向位置
和截面变化系数
确定时,变截面柔性杆的无量纲角频率
的值随着无量纲波数
的增大而趋于一个定值;在截面变化系数
确定时,柔性杆无量纲角频率
的值随着横向位置
的增大减小。由图2中,d图可知,在同一横向位置
处,柔性体无量纲角频率
的值随着截面变化系数
的增大而减小。另外,由式(19)可知,当波数在不稳定范围内时(
),柔性体角频率
与
无关。
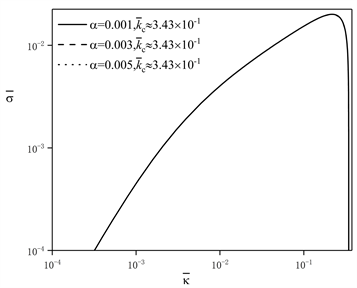
由式(20)可知变截面柔性杆在
处的扰动时间增长率与截面变化系数
无关,故图3中a图为
处,截面变化系数
,弹性模量
不同时扰动时间增长率
与波数
的关系曲线图;图3中的b图为
处,截面变化系数
不同且
时扰动时间增长率
与波数
的关系曲线图。

(a) (
) (b) (
)
Figure 3. The effect of dimensionless wave number on dimensionless the temporal growth rate on
图3. 在
处无量纲波数对无量纲扰动时间增长率的影响
由图3中,a图可知,在
处,截面变化系数
相同时,扰动时间增长率
的值随着弹性模量
的增大而减小。由图3中的b图可知,当波数在不稳定范围内(
)且取
时,在
处,对于不同的截面变化系数
,扰动时间增长率
与波数
关系图重合且
的值亦为先增大后减小且最终趋向于零。
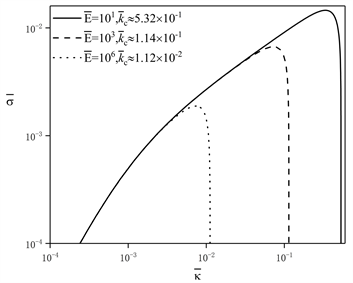
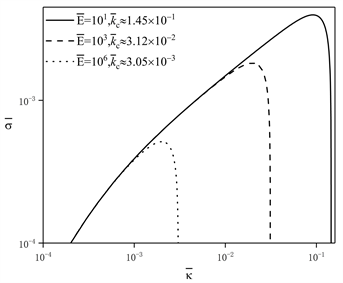
由式(20)亦可得变截面柔性杆在
处的扰动时间增长率与波数的关系曲线图,在图4中,a-c图为
处,截面变化系数
不同时扰动时间增长率
与波数
的关系曲线图;图4中的d图为
处,截面变化系数
不同且
时扰动时间增长率
与波数
的关系曲线图。
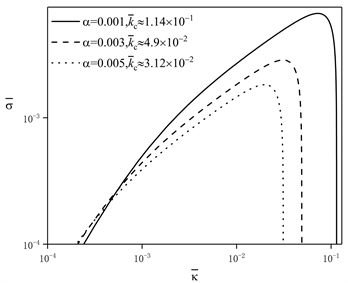
类似地,在图4中,由a~c图可知,在
处,当波数在不稳定范围内(
)且截面变化系数
确定时,扰动时间增长率
的值随着波数
的增大先增大后减小且最终趋向于零;另外,在
处,当截面变化系数
相同时,扰动时间增长率
的值随着弹性模量
的增大而减小。由图4中的d图可知,当波数在不稳定范围内(
)且
时,在
处,扰动时间增长率
的值随着截面变化系数
的增大而减小。它表明了在该横向位置处扰动时间增长率随着截面变化系数的增大而减小,即柔性杆的直径增加时其扰动强度减弱。
5. 结果和讨论
5.1. 最不稳定波数
本文在上一部分的讨论中,得到波数在
范围内的扰动时间增长率图像,如图3图4所示。根据图3和图4中的扰动时间增长率图像可定义一个最不稳定波数
,即柔性体发生耦合运动时,波动最剧烈(扰动时间增长率
最大)时的波数。即
为
时的波数,则由式(20)得:
(21)

(a) (
) (b) (
)(c) (
) (d) (
)
Figure 4. The effect of dimensionless wave number on dimensionless the temporal growth rate of the perturbation with respectively different the cross-section change coefficient and the elastic modulus on
图4. 在
处,截面变化系数和弹性模量分别不同时,无量纲波数对无量纲扰动时间增长率的影响
式(21)为最不稳定波数
的隐式表达式,为了得到
与各参数之间更为直观的关系,本文得到了
时,最不稳定波数
的近似表达式。同种材料在相同的几何特征下,其弹性模量的值反映了其刚度的值。由于本文中所研究的材料为柔性体即刚度较小的材料,根据(21)我们可以求得
时的最不稳定波数
的近似值:
(22)
将式(22)分别带入到(19)和(20)中,得到
时最不稳定波数所对应的角频率和扰动时间增长率分别为:
(23)
(24)
式(22)~(24)为变截面柔性体与流体耦合运动中,其扰动最剧烈时,最不稳定波数、角频率和最大扰动时间增长率的表达式。
5.2. 角频率和波数与风速的关系
本文在5.1的讨论中,得到了
时的
,
和
的近似表达式。现在将
和
引入物理量纲,得:
(25)
(26)
式(25)及(26)给出了变截面柔性杆与流体耦合运动中,扰动最剧烈时的最不稳定波数及角频率与风速的关系式。根据式(25)及(26)可知,角频率是由动压强和惯性的比值所决定的,其值应与风速V成线性关系;波数是由动压强和刚度的比值所决定的,其值应与风速
成线性关系。另外可得到柔性杆耦合运动时的相速度
的值与风速
亦成线性关系。在本文前面的讨论中,没有考虑柔性体本身自重的影响,但本质上,由于自身重力的存在会使柔性杆发生微小的变形。
6. 结论
本文得到变截面柔性杆与气流耦合运动时的方程(气流流速为V),求解后给出了该变截面柔性杆与流体耦合运动时的波扰动时间增长率和特征函数的表达式,并讨论了柔性杆波数小于截至波数(耦合运动不稳定)时,角频率与扰动时间增长率的变化规律。有如下结论:
1) 变截面柔性杆角频率的值随着波数的增长逐渐趋于一个定值;在相同横向位置处其值随着截面变化系数的增大而逐渐减小;在截面变化系数相同时,其值随着横向位置的增大而减小。
2) 变截面柔性杆扰动时间增长率的值随着弹性模量值的增大而减小;在相同横向位置处,其值随着截面变化系数的增大而减小。
基金项目
国家自然基金项目(11472123),国家自然基金项目(11862012)。