1. 引言
激光技术目前在医疗、航天、军事等方面均得到广泛应用,有激光切割、激光快速成型、激光焊接、激光手术、激光武器等,其中激光打标是指利用激光在物体表面留下文字、图案等标记的方法。早期的激光打标系统只能在垂直于激光束的平面上进行加工 [1],随着激光技术和运动控制技术的发展,目前激光打标系统可以处理斜面、自由曲面等问题 [2] [3] [4] [5],其中较常见的系统由多轴机床等运动机构和3D扫描振镜组成 [6]。
激光打标目前存在的一个问题是,将文字等图案映射到曲面上会发生变形。影响图案变形的因素主要有两个方面,一是来源于平面图案到曲面的映射计算,二是源自振镜系统的失真。许多学者已就激光打标机和扫描振镜系统的失真校正做了大量工作,Xie等 [7] 研究了扫描振镜系统的图像畸变矫正算法,并利用矫正算法减小扫描图像的失真误差;Chen等 [8] 提出了一种激光打孔系统中场畸变的补偿算法,利用补偿函数减小系统的畸变误差和位置误差;Wang等 [9] 提出一种线性补偿算法,在数模转换器将数据转换成电信号之前,先对数据进行补偿以提高打标质量;Tu等 [5] 提出一种神经网络算法,建立起物体表面激光点坐标和扫描器控制电压之间的映射关系。上述方法都能一定程度的减小图案的变形,但是由于模型和图案固有的几何特性、映射算法的缺陷等因素,都不能完全解决映射后图案变形的问题。
关于上述算法存在问题,本文提出一种激光打标中的映射算法,该算法将待打标曲面展平为二维平面,建立了曲面与二维平面之间的映射关系,然后在平面内对齐打标图案与展平平面,进而确立平面图案与曲面之间的映射关系,最后通过仿真实验验证了算法的可行性。
2. 激光打标映射算法
将图案映射到模型表面的关键在于建立一种曲面展平的方法,以建立曲面与二维平面之间的映射关系,然后得到平面图案和曲面之间的映射关系。本文提出一种激光打标解决方案,以在曲面的某一区域标记出平面图案,同时尽可能减小图案的变形。
2.1. 待打标曲面展平算法
本文主要针对三角网格模型,平面图案由离散点序列近似表示。三角网格模型T由其顶点集
和三角面片集
组成,其中
为一个三角网格的三个顶点,其中点集
进一步可以分为内部顶点
和外缘顶点
。已知平面图案由一组曲线
组成,每一条曲线
可以由离散点集
近似表示;平面图案的边界点集为
,其中
;网格模型上打标曲面的边界点集为
;
中的每个点在
中都能通过相同的索引找到对应点。
建立打标曲面与展平平面映射关系算法主要分为3步,首先映射网格曲面的边界点,然后映射除边界点以外的内部点,最后映射网格的三角面,即可构建网格曲面与二维平面之间的映射关系。
2.1.1. 弧长法映射外缘顶点
采用弧长法映射外缘顶点,如图1所示,假设外缘顶点
介于顶点
与
之间,
与
分别表示其位置向量,其映射在曲面上的顶点
由位置向量表示如式(1)所示。
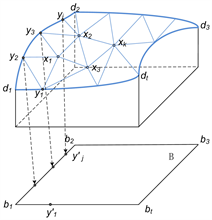
Figure 1. Map exterior vertices using arc length proposition method
图1. 映射外缘顶点示意图
(1)
其中,
表示三角网格上顶点
和
之间的弧长,
表示映射平面上两个顶点之间的距离。
2.1.2. 凸映射算法映射内部顶点
利用凸映射算法将内部点映射到二维平面,记对应的映射点集为
,如图2。映射后要求三角网格各边之间没有交叉,交叉点仅存在公共顶点处;另外要求映射面中的小平面尽可能保持原始形状 [10]。基于凸映射算法映射内部顶点 [10] [11] [12],其基本思想是将映射后的内部点
看做其邻域的凸组合,如式(2)。
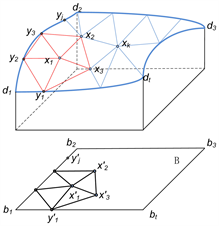
Figure 2. Map interior vertices using convex mapping
图2. 映射内部顶点示意图
(2)
其中系数满足:
(3)
上述方程式表示映射的内部点
同其邻域中的点都可以组成凸组合,即位于同一个凸包内,如果与邻域点组成的是凸多边形,则多边形内部各条边没有交叉。内部点
关于方程式(2)可以组成一个线性方程组,如果外环多边形
是凸多边形,根据论文 [11] [12] [13] [14] 证明可知其解
是唯一存在的。
内部顶点 和其映射点
和其映射点 具有相同的三角网格结构,因此求解凸映射算法简化为计算凸缘系数
具有相同的三角网格结构,因此求解凸映射算法简化为计算凸缘系数 和求解线性方程组。基于三角网格结构
和求解线性方程组。基于三角网格结构 ,
, ,采用论文 [10] [11] [12] 类似的方法计算
,采用论文 [10] [11] [12] 类似的方法计算 ,以满足保持形状不发生严重变形的要求。伪代码如表1所示。
,以满足保持形状不发生严重变形的要求。伪代码如表1所示。

Table 1. Pseudo-code mapping interior vertices
表1. 映射内部顶点算法
2.1.3. 采用线性插值映射三角面片
原始三角网格模型与展平后的三角网格之间的对应关系,可以利用三角网格的重心坐标创建,如图3所示, 为原始模型上某三角面片
为原始模型上某三角面片 中的任意一点,
中的任意一点, 与三角面片
与三角面片 为其映射对应部分,两者具有相同的重心坐标
为其映射对应部分,两者具有相同的重心坐标 。
。
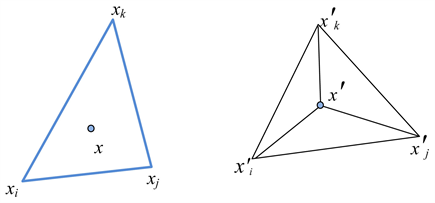
Figure 3. Map whole facet surface using linear interpolation
图3. 映射三角面片示意图
基于 ,
, ,
, ,可以得到:
,可以得到:
 (4)
(4)
三角网格 中映射点
中映射点 坐标计算公式为:
坐标计算公式为:
 (5)
(5)
如图4所示,上图为待打标模型的三角网格示意图,下图为利用上述算法得到展平后的平面网格,上图中的每一个三角网格在下图中都能找到相对应的网格。

Figure 4. Example of shape preserving facet surface flattening
图4. 三角网格展平示意图
2.2. 映射图案到模型表面
在模型曲面被展平以后,可以通过两步将平面图案包裹到物体模型表面:1) 将待打标图案与通过展平曲面得到的二维平面对齐,使得图案中的每个离散点在平面中都有确定的坐标;2) 利用上节构造的三角网格与展开平面之间的映射关系,将图案映射到三维网格模型上。
如图5中(a)所示为待打标平面图案局部示意图,将平面图案与网格曲面展平得到的平面对齐,这样图案就与三角网格模型建立了映射关系,如上图(b)所示。例如图案中G的一个顶点 根据映射关系进一步得到
根据映射关系进一步得到 在原始网格中的坐标,记为
在原始网格中的坐标,记为 ,如图(c)所示,即可将平面图案映射到三角网格模型的曲面上。
,如图(c)所示,即可将平面图案映射到三角网格模型的曲面上。
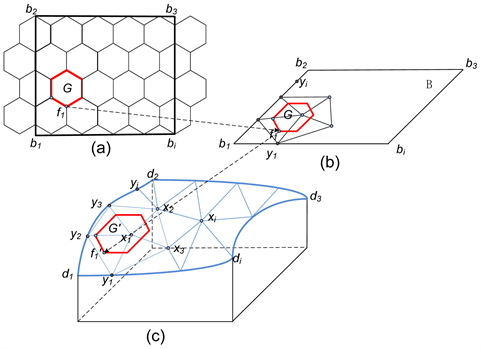
Figure 5. Mapping pattern to sculpture surfaces
图5. 图案映射流程示意图
为了验证上述算法的有效性,基于Microsoft Visual Studio 2015平台,使用C++作为开发语言,开展以下仿真实验。如图6所示为汽车面板的三角网格模型,首先利用展平算法将其映射到二维平面上,映射后效果如图4所示。然后将待打标六边形图案和展平后的平面对齐,以建立图案和三角网格模型之间的映射关系,同时还能保证打标到模型孔隙上的图案被去除掉。

Figure 6. Triangular surface of the car’s frontal
图6. 汽车面板三角网格模型
根据图7可以看到,映射到曲面上的图案整体没有发生严重的变形,如图中A1倾斜区域效果亦较好;但由于局部曲率变化较大,如图中B1区域,图案打标后发生轻微的扭曲变形。
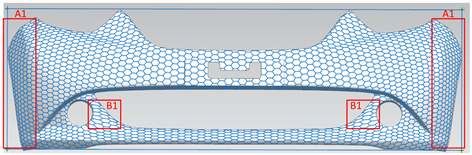
Figure 7. Laser marking simulation result of the car’s frontal
图7. 汽车面板激光打标仿真结果
3. 结束语
针对激光打标中图案变形问题,本文提出一种映射算法,该算法首先将三维网格曲面展平到二维平面内,然后在二维参数域内建立图案与网格的对应关系,进而建立二维平面图案与三角网格曲面之间的映射关系。由于物体模型自身结构的限制,保持打标前后图案形状完全不变较为困难,目前各种算法的目的只能尽可能减小变形。通过上述仿真实验看出本算法实际效果较好,变形量控制在合理范围内。
基金项目
国家自然科学基金资助项目(51575386)。
NOTES
*通讯作者。