1. 引言
中国致密气勘探开发经历了探索起步阶段、规模发现阶段,目前正处于快速发展阶段,是接替常规油气能源的重要力量,具有巨大的经济价值与社会价值 [1] [2]。致密气藏具有储集层物性差、渗流能力差、经济效益差等特点 [3],需要通过水力压裂技术和水平井钻井技术产生增产改造体积(SRV),提高致密气藏资源的开发效益。采用Arps产量递减等传统分析方法对于非常规气井已经不再适用 [4],因此有必要探索新的方法和技术,能高效进行致密气藏压裂水平井的生产动态分析,为致密气藏产能优化服务,提高经济效益。
致密气藏压裂后生产动态分析方法主要有三种。第一种是解析法 [5] [6] [7] [8],其优势是求解简单、计算速度快。但该类方法对于复杂裂缝形态刻画多以均匀和对称裂缝为主,裂缝间干扰采用设置不渗透边界进行分区,因此,该方法在储层非均质性和复杂结构井的刻画方面存在很大局限性。第二类方法是在源函数基础上建立的半解析方法 [9] [10],通过划分微元体离散裂缝,建立储层及裂缝系数矩阵,迭代计算稀疏矩阵进行求解,该类方法考虑了裂缝的形态对生产动态的影响,但在裂缝三维非平面研究以及外边界区域划分方面存在局限。第三类是数值模拟方法 [11] [12] [13],该类方法结合微地震数据刻画近似的增产改造体积模型,再利用网格离散技术和数值计算方法,能准确地描述压裂后复杂缝网的形态及储层渗流特征,可以分析裂缝大小、裂缝间距、裂缝传导率等参数对生产动态的影响 [14] [15]。但是数值模型计算复杂,耗时耗力。
总体而言,以上提到的解析法/半解析法运算速度较快但仅适用于均质储层,数值模拟法可以精确地计算非均质储层的复杂几何形状井,但非常耗时。本文通过深入认识致密气藏的储层和流体流动特征,提出一种致密气藏生产动态分析的新方法 [16] [17] [18],即快速推进法(FMM)。FMM最早是由Sethian J. A.于1999年提出来的一种计算波前运移情况的方法 [18]。快速推进法是一种高效追踪边界运移情况的方法,经过几十年的发展,广泛应用于医学、地质学等领域 [19]。Jiang Xie等利用波前快速推进法对储层的动用情况进行预测,即使针对百万级的网格,也仅仅需要十几分钟的时间,大大提高了网格计算的效率 [20]。快速推进法既能准确计算非均质储层复杂结构井的生产动态,又能提高计算效率,这对于致密气藏的高效开发和评价意义重大。
2. 数学模型
采用快速推进法分析致密气藏的动态,首先是建立考虑流体特征的扩散方程,然后采用快速推进法求解致密气藏扩散方程,结合几何近似法圈定扩散时间内的泄气体积,进一步分析生产动态。相比水和油,气体是高度可压缩流体,气藏的孔隙度、压缩系数和粘度等参数高度依赖孔隙压力,致密气藏的高度可压缩性表现尤为明显。以拟压力和拟时间形式代表压力和时间,可以充分地考虑气体的高度压缩性。
2.1. 扩散方程的建立
致密气的密度随压力的变化明显,具有高度压缩性,引入气体状态方程,根据质量守恒定律,推导得到物质平衡方程:
(1)
式中,p为气体压力,Mpa;
为渗透率,mD;μ(p)为气体粘度,mpa·s;Z(p)为天然气偏差因子,无因次;
为储层孔隙度,无因次。
已知,气体压缩系数Ct(p)表达式如下:
(2)
方程(2)进一步推导得到
(3)
定义气体拟压力和拟时间如下式所示:
(4)
(5)
其中,i代表原始地层压力条件下。将方程(3)~(5)带入方程(1),可以得到致密气藏的渗流微分方程如式(6)所示:
(6)
将方程(6)进行傅里叶变换得到:
(7)
方程(7)的渐进解为:
(8)
进一步推导得到方程(8)的程函方程形式:
(9)
其中,
描述了拟压力m(p)的压力波前缘传播时间,
代表扩散系数,其定义式如下:
(10)
2.2. 压力波传播时间的求解
高效求解压力波前缘传播的程函方程是快速计算致密气井生产动态的关键。快速推进法(FMM)通过沿压力传播轨迹积分计算传播时间,然后采用有限差分迎风格式快速计算扩散时间,定量表征压力波在非均质储层中传播速度。具体的计算过程为首先在笛卡尔坐标网格中,将方程(10)写成有限差分格式,对τ值进行校正 [21],校正结果如方程(11)所示。标准有限差分因子D在±x方向可写成
和
。±y方向可写成
和
。式(11)中认为“未知点”的τ值是无穷大,用最大方程以保证迎风格式。可根据常规有限差分公式计算四个象限(底左,底右,顶左,顶右)的τ值,选择最小τ值作为“已得到点”传播时间。
(11)
图1为FMM计算流程示意图。首先将所有网格节点标记为“未知点”,生产井位置节点赋τ值为0,标记为“已得到点”(红色实心点)如图1(a)所示。接下来定位“已得到点”的邻近未知节点A,B,C和D,标记为“考虑点”(圆圈),同时计算这四个点的压力前缘传播时间,将传播时间值标记在图1(b)线,“考虑点”圆圈里面的数字是压力波从原点传播到该节点的累计τ值。图1(c)中选择最小τ值点(如点A),标记为“已得到点”,同事添加A点相邻的E,G和F点为“考虑点”,计算它们的τ值如d所示。经过计算,D点的τ值最小,作为新的“已得到点”。以此类推直到压力波前缘传播到整个网格。
根据几何近似法,扩散方程传播时间τ和实际时间t之间的关系如方程(15)所示 [22],以此可计算每个单元网格的实际传播时间,式中Vp(τ)为泄气体积,m3。
(12)
2.3. 致密气井生产动态分析
常规方法通过计算压力波传播速度来表征生产动态,而快速推进法是通过标记压力波传播时间来开展生产动态分析,具有准确和速度快的特点,这是快速推进法分析致密气井生产动态的核心优势。基于压力波扩散时间的计算,通过圈定和总和压力波前缘传播的网格作为生产井泄气体积,结合压力波前缘传播位置与实际传播时间的关系,可定量计算储层泄气体积随着时间的变化关系。而定产条件下压力和定压条件下产量的表达式分别为方程(13)和(14) [22] [23],从而开展致密气藏生产动态分析。
定产条件下压力解:
(13)
定压条件下产量解:
(14)
3. 模型验证
3.1. 物理模型
致密气藏多采用多级压裂水平井进行商业化开采,基于致密气藏储层的致密性和人工裂缝大幅提高储层渗透性的基础理论,假设人工裂缝渗透率远远高于致密气藏储层渗透率,构建如图2所示的增产改造三维模型,模型假设图中水平井的长度L = 1000 m,裂缝半长xf = 110 m,裂缝条数M = 3,裂缝间距250 m,其他储层参数如表1所示。

Figure 2. Schematic diagram of tight gas multistage fracturing horizontal well model
图2. 致密气多级压裂水平井模型示意图

Table 1. Basic reservoir parameters of fractured horizontal wells in tight gas reservoirs
表1. 致密气藏压裂水平井储层基本参数
3.2. 模型验证
为了验证快速推进法的准确性,对比了快速推进法(FMM)和商业数值模拟软件CMG在定产条件下的井底压力响应,气井以q = 5 × 104 m3/d的产量稳定生产,相关参数同表1所示,图3为快速推进法(FMM)和CMG的井底压力响应结果,可以看出快速推进法(FMM)和CMG的模拟结果得到了很好的吻合,并且FMM方法的运算速度比CMG提高了11%,验证了快速推进法(FMM)的准确性与高效性。
4. 生产动态分析工作流程
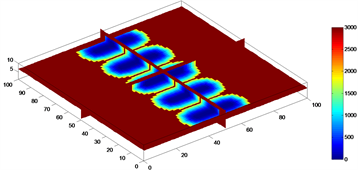
根据致密气藏的储层特征,建立一个具有5条无限导流裂缝的压裂水平井理想模型,相关储层参数如表1所示。运用Matlab软件编程实现压力波前缘传播时间的计算和可视化。对于致密气藏,储层非常致密,只有经过压裂改造,才能取得工业油气流。在增产体积区域的渗透率普遍高于未改造区域(基质),因此基质中的压力波前缘传播的速度明显慢于增产改造区域部分。从图4(a)中可以看出,压裂改造区域的扩散时间远远小于非改造区域。图4(b)和图4(c)分别展示了该理想模型在生产1个月和10年的泄气区域。
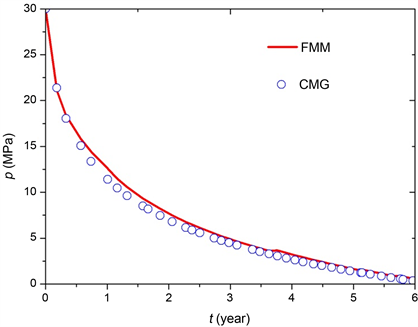
Figure 3. Comparison of bottom hole pressure calculated by FMM and CMG in unconventional gas wells
图3. 非常规气井FMM和CMG计算的井底压力结果对比
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 4. Calculation process of gas drainage volume of multiple fractured horizontal well in tight gas reservoir. (a) The diffusion time (106 s); (b) Drainage area of one month; (c) Drainage area of 10 years
图4. 致密气藏压裂水平井泄气体积计算过程。(a) 扩散时间(106 s);(b) 1个月的泄气区域;(c) 10年的泄气区域
根据几何近似法的相关理论,圈定特定时间内压力波前缘传播到的储层体积,找出压力波及体积与生产时间的关系,可将跟储层物性参数紧密相关的压力波传播时间与生产压力、产量有效地联系起来。根据方程(13),可以计算出该理想模型井在定产条件下的压力响应。根据油田实际生产经验,假设该井在q = 4.5 × 104 m3/d,5 × 104 m3/d和5.5 × 104 m3/d三种定产条件下生产,预测了压裂水平井井底压力随着生产时间的变化趋势,如图5所示。从图中可以看出,随着生产的进行,井底压力在生产初期阶段压力下降速度很快,后期下降速度不断变缓。且配置的产量越大,压力下降越快。假设该井合理生产时间为20年左右,配产5 × 104 m3/d较为合适。

Figure 5. Pressure prediction of multiple fractured horizontal well in tight gas reservoir under constant production rate
图5. 致密气藏压裂水平井定产条件下压力预测
同理,根据公式(14)可预测致密气藏压裂水平井在恒定生产压差的条件下的产量递减情况。图6为致密气藏理想模型在生产压差为2 MPa,4 MPa和6 MPa的条件下的产量递减响应情况。从图中可以看出,生产压差越大,初期产量越高,递减速度越快,后期产量趋于平稳,但生产压差越大,后期的稳产产量越低。这主要是由于致密气压裂水平井为封闭边界,总可采储量一定,生产压差越大,早期产出的气体越多,后期的供应不足导致后期的产量偏低。根据定产条件下的压力预测结果,稳产20年的合理配产量为5 × 104 m3/d (图5),基于图6的预测结果,稳产产量5 × 104 m3/d的生产压差设置为2 MPa较为合适。

Figure 6. Production prediction of multiple fractured horizontal well in tight gas reservoir under constant pressure
图6. 致密气藏压裂水平井定压条件下产量预测
5. 结论
结合快速推进法,以致密气藏为研究对象,提出了一个分析致密气藏的复杂结构井(压裂水平井等)生产动态的半解析方法。首先考虑了气体的高度压缩特征和储层非均质性,推导出致密气藏压力波前缘扩散方程的程函方程形式,通过运用快速推进法可快速、有效地解方程。然后总和所有压力前缘波及到的孔隙体积,定量表征了该井的泄气体积随时间的变化关系。将扩散时间转化为实际时间以后,通过Matlab编程软件实现扩散时间和动用孔隙体积可视化,有效地分析了致密气藏生产动态,主要得出以下几点结论:
1) 常规方法通过计算压力波传播速度来表征生产动态,而快速推进法是通过标记压力波传播时间来开展生产动态分析,具有准确和速度快的特点,这是快速推进法分析致密气井生产动态的核心优势。
2) 致密气藏生产动态分析新方法具有准确性和高效性。基于笛卡尔坐标网格开展压力波前缘传播时间计算,能同时考虑储层的非均质性和井的复杂结构,能较准确地模拟致密气藏的流体流动。并且新模型与数值模拟软件CMG计算结果吻合程度高,计算速度提高了11%,验证了计算模型高效性。
3) 快速推进法(FMM)具有灵活的运用形式,结合几何近似法,分别在定压条件下预测产气量和在定产条件下预测井底流压,根据产量压力动态响应进行合理配产。可快速地估算定压生产和定产生产情况下的井动态特性。快速推进法对构造条件简单的致密气藏生产动态分析,具有很好的应用价值。
基金项目
国家油气重大专项“彭水地区常压页岩气富集规律与目标优选”(2016ZX05061-001-002)。