1. 引言
风蚀是侵蚀生态系统中的一种驱动因素。为了研究侵蚀生态系统中风蚀的动力学机制,本文建立了风蚀–植被动力学方程。研究表明,时间离散的系统会产生Neimark-Sacker分岔,并且进一步能形成周期环、倍周期分岔等非线性过程 [1] [2] [3]。动力学分析是探究系统分岔方式的常用手段,基于理论进行分岔分析,并结合数值模拟可以得到系统的分岔图与相位图。分岔图与相位图能够直观展现风蚀–植被系统中Neimark-Sacker分岔引起的各种动力学过程。
2. 模型构建与分岔分析
在地表风力侵蚀过程中,植被的存在可以减弱风力强度。并且植被的根茎部分能够增强土壤的凝聚力从而减小风力对地表的剥蚀 [4]。在风蚀地区,植被与沉积沙的相互作用关系复杂。本文将植被对沉积沙的影响分为两个部分。1) 植被的阻沙作用:植物的繁茂枝叶对风沙流中的沙粒具有拦截作用。植被的存在使得风成沙的沉积率增加 [5] [6]。2) 植被的固沙作用:改变了沙表性质,使其起动风速阈值大于当地最大风速值等条件。同样的,空气中的沙子沉积到植被所覆盖的区域后,也会对植被的生长产生影响。例如,风力对地表的剥蚀作用可以给植物带来生长所需的无机营养物质。从这方面上讲,风蚀的分离作用会对植被起到一定的促进作用。另一方面,沉积沙的增加对植被有一定的掩埋作用,则植物就需要进一步的生长以裸露出足够多的部分,以保证地面部分进行光合作用。风力侵蚀分为风蚀、搬运和沉积过程,这三个过程对植被均有不同的作用影响。
根据植被–沉积沙相互作用关系与先前的研究工作 [7] [8],将植被的覆盖度和沉积沙的高度作为状态变量,得到了离散的风蚀–植被动力学模型映射关系:
(1)
其中,km:最大植被覆盖度下沉积沙沉积速率(cm year−1);D:植被对沉积沙的影响系数(cm−1 year);a:沉积沙对自身高度的抑制系数(year−1);b:植被对沉积沙的固定作用系数(cm−1);g:沉积沙高度变化对植被生长的抑制系数(month cm−1);
本文中依据Guckenheimer和Holmes [9] 述的Neimark-Sacker分岔定理,解得系统(1)的两个平衡点分别为
,
。因此,映射(1)在点(s, v)所对应的雅克比矩阵为:
(2)
其中
(3)
(4)
将
代入方程(2)可得:
(5)
在给均匀定态解
加入微扰后,将
代入雅可比矩阵可得:
(6)
其中
(7)
结合上述方程,我们分别可以得到雅克比矩阵J1的迹和行列式:
(8)
从而解得对应的雅克比矩阵的特征值:
(9)
Neimark-Sacker分岔条件之一是方程(9)的特征值为一对模为1的共轭复数 [10]。这就要求:
,且
。解得
(10)
其中
,
。
然后我们通过下式将均匀定态平衡点
平移至原点,令
(11)
将式子(11)代入式子(2)中,经泰勒展开可以得到如下映射,
(12)
其中
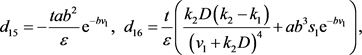
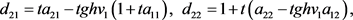
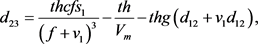
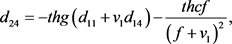
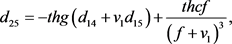
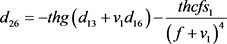 (13)
(13)
Neimark-Sacker分岔的第二个条件是
 (14)
(14)
 (15)
(15)
方程(14)等价于式子(8)中的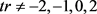 。由于在方程(9)中
。由于在方程(9)中 ,则进一步改写条件为
,则进一步改写条件为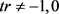 ,即
,即
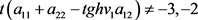 (16)
(16)
再基于映射(12)的规范型进行Neimark-Sacker分岔分析,应用可逆变换:
 (17)
(17)
代入映射(12)后得,
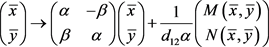 (18)
(18)
其中
 (19)
(19)
当条件(19)被满足时 [11],系统(17)在点(0, 0)处产生Neimark-Sacker分岔。
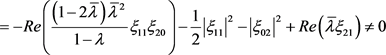 (20)
(20)
其中
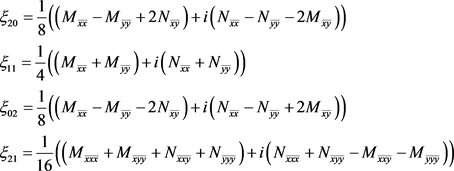 (21)
(21)
且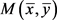 和
和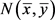 在
在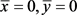 处的二阶偏导数与三阶偏导数为:
处的二阶偏导数与三阶偏导数为:
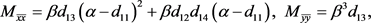
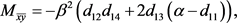
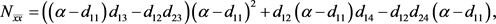
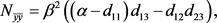
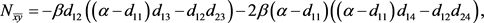
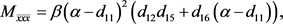
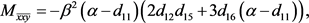
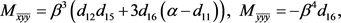
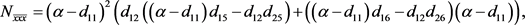
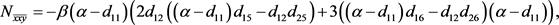
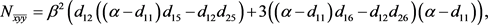
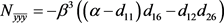 (22)
(22)
结合方程(19)、(20)、(21),可以解得,
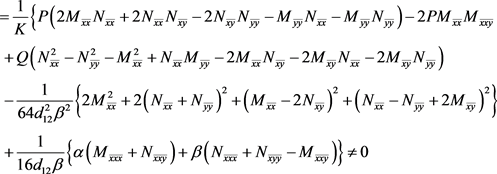 (23)
(23)
其中,
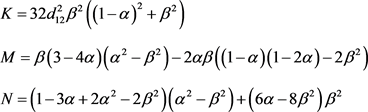 (24)
(24)
当条件(10),(14),(16)和(23)都被满足时,系统(1)在 处产生Neimark-Sacker分岔。如果式子(14)、(20)满足
处产生Neimark-Sacker分岔。如果式子(14)、(20)满足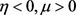 ,产生的Neimark-Sacker分岔是超临界的,系统在平衡点
,产生的Neimark-Sacker分岔是超临界的,系统在平衡点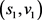 处失稳,进而导致系统中周期环的出现。
处失稳,进而导致系统中周期环的出现。
3. 数值模拟结果
在上一节内容中我们已经得到了系统的分岔条件,即当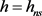 时,系统达到临界点,当
时,系统达到临界点,当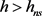 时,系统发生Neimark-Sacker分岔。本节通过数值模拟展现参数变化时风蚀–植被系统的Neimark-Sacker分岔以及由分岔所引起的复杂动力学行为。当我们令参数值分别为k0 = 5; km = 30; D = 0.1; a = 1; b = 0.04; Vm = 100; c = 0.5; f = 10; ε = 12; g = 0.01,便可以得到如图1所示的特征值曲线图。红色曲线代表的是随着植被生长系数h的增大,系统从均匀稳定态过渡到不稳定状态的过程。
时,系统发生Neimark-Sacker分岔。本节通过数值模拟展现参数变化时风蚀–植被系统的Neimark-Sacker分岔以及由分岔所引起的复杂动力学行为。当我们令参数值分别为k0 = 5; km = 30; D = 0.1; a = 1; b = 0.04; Vm = 100; c = 0.5; f = 10; ε = 12; g = 0.01,便可以得到如图1所示的特征值曲线图。红色曲线代表的是随着植被生长系数h的增大,系统从均匀稳定态过渡到不稳定状态的过程。
在图1的基础上,我们绘制了如图2所示的系统(1)随着参数h变化的分岔图。其中图2(a)和图2(c)分别为沉积沙与植被的分岔图,图2(b)和图2(d)为与其对应的局部放大图,展示了离散系统在趋于混沌过程中所产生的倍周期分岔过程。从图2(a)和图2(c)中可以看到,当h < 0.1489时,沉积沙变量S与植被变量V处于渐进稳定状态。当系统越过临界点即h > 0.1489时,系统的稳定态消失,并开始在渐进不动点附近产生分岔。如图2(b)和图2(d)所示,随着参数h的不断增大,系统会经历倍周期分岔过程。
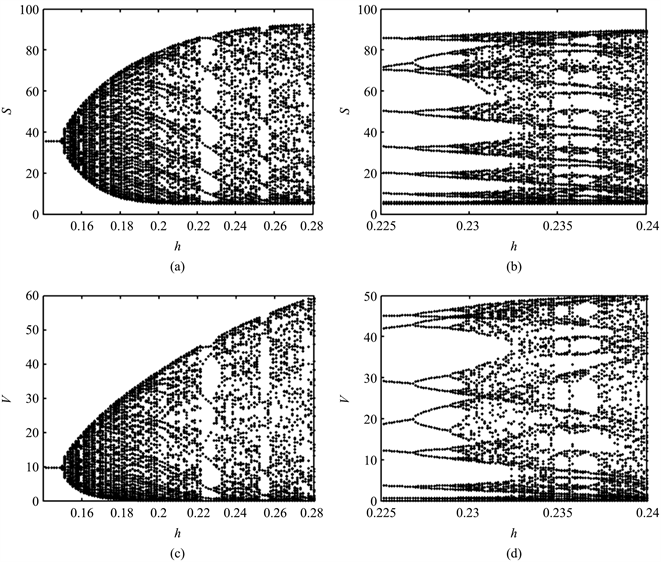
Figure 2. (a) and (c) are bifurcation diagrams, (b) and (d) are corresponding partial enlarged diagrams
图2. (a)和(c)为分岔图,(b)和(d)为对应的局部放大图
为了更直观地观察在混沌路径上,离散系统的吸引子是如何随着参数而发生改变的,我们得到了如图3所示的相位图。图3(a)与图3(b)清晰地展示了系统从不动点到拟周期的转变过程。再随着参数h的增大,又经历了不变环(图3(c))以及倍周期过程(图3(d))。
大量研究成果表明 [12] [13] [14],在离散动力学系统研究领域中,Neimark-Sacker分岔是最重要的分岔之一。本文在时间离散风蚀–植被模型中,应用Neimark-Sacker分岔来探究植被与风成沙的复杂动力学机制。从图3可以观察到,对于不同生长速率的植被而言,存在与沙丘的动态平衡机制。风蚀地区的植被生长受当地气候影响,在不同时期有着较大的区别,这意味着风蚀–植被系统很难保持在稳定平衡状态。且从图3可以看到植被覆盖度越高,沙丘则越大,表明了植被覆盖促进了沙丘的增长与稳定存在。在本文中,我们通过改变植被生长系数h的大小,发现植被生长系数与沙丘的大小成正相关。动力学分析作为一种重要的研究方法,其可以通过大量的数值模拟来展现出各个环境因素对整个系统的影响。
基金项目
本研究受到国家水污染控制与治理科技重大专项(No. 2017ZX07101003-06)的资助与支持。
NOTES
*通讯作者。