1. 引言
空气过滤器被广泛地应用于特种车辆进气系统,过滤空气中的灰尘和杂质,以减少对车辆发动机气缸、活塞环和其它精密零部件的磨损,延长动力设备的使用寿命。空气过滤器的进气阻力性能参数直接影响动力设备的动力性、燃油(气)经济性、使用可靠性和耐久性等 [1]。空气过滤器的内部流动十分复杂,涉及到三维紊流流动、多孔介质流动、多相流等。受空气过滤器内部复杂结构和工作环境的限制,要完全真实地了解其内部流动特性十分困难,依靠经验和试验手段来研制空气过滤器不但浪费大量的人力、物力,花费大量的时间,还无法给出空气过滤器内部的全面流动信息。随着计算机技术的飞速发展,计算流体动力学(CFD)技术被用来研究空气过滤器的速度场、压力场等问题 [2]。国外一些学者对褶型滤芯过滤器过滤压力损失模型进行研究 [3] [4],并对空气过滤器进行CFD数值模拟 [5] [6]。
对空气过滤器进行数值模拟的思路是:首先,对滤芯进行台架试验,得到滤材和滤芯的阻力特性数据;其次,选择滤芯的多孔介质数学模型,通过试验数据,计算得到多孔介质的模型参数;再次,建立空气过滤器的三维模型,将多孔介质渗透模型代入,利用CFD软件计算得到空气过滤器的阻力特性;最后,通过试验台验证空气过滤器仿真分析结果。由此可以看出,进行空气过滤器的数值模拟分析,滤芯的台架试验,即多孔介质渗透模型的建立,是数值模拟的基础。由于滤材台架试验的硬件设备要求较高,试验周期较长,导致空气过滤器设计的周期长。同时,滤材试验测试准确性等不确定性因素也影响了数值模拟结果的准确性。
本文采用GeoDict材料分析软件,将一种滤材的电子计算机断层扫描照片生成接近真实结构的三维滤材模型,并进行仿真计算,从而得到滤材的性能数据,以此数据为基础,得到滤材的多孔介质渗透模型,进而得到了空气过滤器的阻力特性曲线。最后,通过试验台架对空气过滤器的阻力特性进行验证可行性。
2. 空气过滤器数值模拟
2.1. 过滤材料的数值模拟
德国学者Albrecht和Kaufmann最早对过滤器进行研究,他们针对纤维垫开始气溶胶过滤机理的理论探讨。此后,国际上许多学者对过滤器的性能进行了试验和数值研究,并在试验的基础上提出了过滤材料经验模型。在低流速、小雷诺数的情况下,多孔介质两端的阻力分布服从达西定律:
式中:
——介质两端之间的阻力,Pa;
——流体的动力黏度,Pa·s;
——流量,m3·h−1;
h——过滤介质的厚度,m;
A——过滤介质的面积,m2;
K——达西常数。
对于纤维介质,流速v = qV/A,达西常数为:
式中:dF——纤维的直径,m;
f(a)——Davies建议的无纲量力。
研究者将过滤器的阻力一般表示成无因次阻力f(a)的函数:
f(a)是无因次阻力,仅仅是填充密度
的函数。
Happle假设每根圆柱外面由一半径为r (圆柱中心间的距离为2r)的同轴圆柱包围,且假设圆柱表面的剪切应力为零,Happle给出了无因次阻力的表达式为:
Kuwabrara的脑壳模型和Happel的基本相同,只不过该模型不再假设包围在纤维周围且与纤维同轴的外圆柱表面上的剪切应力为零,取而代之的是该表面上旋度为零,Kuwabrara将f(a)表示为:
Hennry利用数值方法求解了交错排列圆柱纤维周围的流场,并得出了以下的无因次阻力:
Rao在Davies研究的基础上,将无因次阻力整理成以下经验公式:
Davies进行了大量的试验研究,得出了关于阻力的关联式,该关联式证明了在0.006~0.3范围内是准确的。在Davies关联式基础上无因次阻力可以表示成如下经验公式 [7]:
虽然可以采用经验公式对滤材阻力特性进行计算,但由于过滤材质的纤维结构不同,因此计算后的阻力结果与试验结果存在较大误差。
2.2. 过滤材料三维模型的构建
本次试验采用某空气滤芯通用过滤材料,其面密度为115 g/m2,平均厚度为0.55 mm。通过电子计算机断层扫描电镜在滤材的高度方向进行扫描,得到一组二维滤材切面照片共900张 [8]。样品扫描所用精度0.834微米,灰度分割阈值150。从结构的每层固体体积比(Solid Volume Fraction, SVF)分析来看,该滤纸的SVF呈现梯度分布,在入流防线先由低到高,又由高到低分布,梯度比较对称。平均SVF比率为13.5%左右,也就是孔隙率86.5%。图1是其中的1张照片导入照片电镜效果图。

Figure 1. One CT picture of Filter material and import electron microscope effect pictures
图1. 滤材电子计算机断层扫描照片和导入照片电镜效果图
GeoDict材料分析软件可以将过滤材料电子计算机断层扫描照片,电子计算机断层扫描与计算机软件结合能够对过滤材料进行无损扫描并对图像重构,进而定量分析滤材孔隙率的变化、数目和分布 [8],生成三维模型,从而进行材料特性分析如孔径分布、流电阻率(渗透性、压降)、热导率、电导率、过滤效率等。
采用GeoDict材料分析软件中的ImportModule模块对滤材的CT扫面照片进行重组,得到如图2所示三维模型。

Figure 2. Three dimensional of filter material with GeoDict software
图2. GeoDict材料分析软件生成的滤材三维模型
2.3. 过滤材料阻力特性的数值模拟
通过对滤材三维模型的计算,得到滤材的结构数据为:厚度0.55 mm,最大孔径35 μm,平均孔径17 μm,这与滤材出厂测试数据量一致。
使用GeoDict材料分析软件中的Flowdict模块,对生成的滤材三维模型进行计算。计算中共设定了7个流速点,并分别对每个流速点进行了滤材阻力特性仿真,计算结果如表1所示。

Table 1. The simulation results of resistance properties for filter material
表1. 滤材阻力特性仿真结果
图3~5是通过滤材的流速为0.02 m/s时,滤材数值模拟结果。

Figure 3. Pressure cloud chart of filter material when the flow rate is 0.02 m∙s−1
图3. 流速为0.02 m∙s−1时滤材压力云图
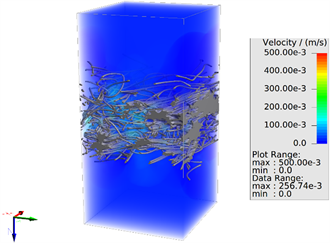
Figure 4. Velocity cloud chart of filter material when the flow rate is 0.02 m∙s−1
图4. 流速为0.02 m∙s−1时滤材速度云图

Figure 5. Velocity streamline diagram of filter material along thickness direction when the flow rate is 0.02 m∙s−1
图5. 流速为0.02 m∙s−1时滤材厚度方向速度流线图
2.4. 空气过滤器的数值模拟
本次试验采用的空气过滤器是双级复合式空气过滤器,这种空气过滤器常用于空气含尘量较大的重载军用车辆上。数值模拟之前,首先对空气过滤器进行模型简化,得到可用于CFD计算的流体结构模型,两种模型如图6所示。

Figure 6. Air filter model and simplified model
图6. 空气过滤器模型和简化后结构模型
空气过滤器流体模型分成了3个计算域,即进口流体域、滤芯流体域(多孔介质)和出口流体域。因此,需要先对滤芯流体域(多孔介质)进行设定,才可以进行空气过滤器的数值模拟 [9] [10]。
多孔介质渗透模型的动量方程是在标准动量方程的后面加上动量方程源项。源项包含2个部分:黏性损失项和惯性损失项。
式中:Si——i向(x, y, or z)动量源项;
D和C为规定的矩阵;
——动力黏度,Pa·s;
vmag——速度矢量值,m·s-1;
vi——i方向速度值,m·s-1。
在多孔介质单元中,动量损失对于压力梯度有贡献,压降和流体速度(或速度方阵)成比例。在简单、均匀的多孔介质上,可以简化模型得到:
式中:a——渗透性系数;
C2——惯性阻力因子。
将D和C矩阵简化为对角阵,对角上的系数分别为1/a和C2,其余项为零。
此种模型是对Darcy定理的修订,使得Darcy定理应用性更广泛。
在Fluent仿真分析软件中,还有一种将源项Si设定为速度的幂函数型的方法,其经验公式如下所示:
式中:C0和C1为自定义经验系数。
在幂函数模型中,压降是各向同性的,C0的单位为国际标准单位。
将之前滤材阻力特性数值模拟计算结果代入2种多孔介质渗透模型中计算,得到空气过滤器两组阻力特性仿真数据和图形,如表2和图7所示。

Table 2. Simulation results of resistance properties for air filter
表2. 空气过滤器阻力特性仿真结果
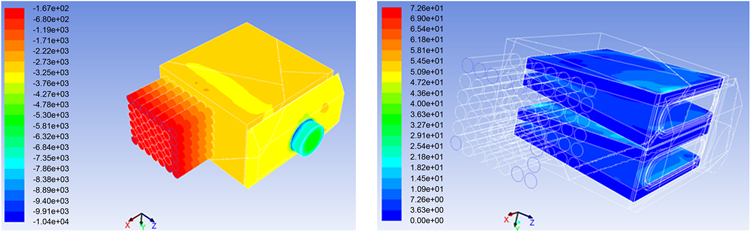
Figure 7. Pressure cloud chart of air filter when the outlet flow rate is 1100 m3∙h−1
图7. 空气过滤器在出口流速1100 m3∙h−1时的压力云图
3. 仿真结果与试验结果对比
3.1. 过滤材料阻力特性试验结果
在过滤材料试验台上,对本次数值模拟的滤材进行了阻力特性试验,试验结果如表3所示。

Table 3. Test results of resistance properties from filter material
表3. 滤材阻力特性试验室结果
通过表1和表3,得到滤材阻力特性的试验与仿真对比曲线如图8。从图8可以看出,滤材阻力特性的仿真与试验结果基本吻合。由此可以看出,采用GeoDict材料分析软件计算得到的材料特性曲线接近理想测试结果,能够得到滤材准确的阻力特性,可以给空气过滤器总成数值模拟提供准确的多孔介质边界条件。
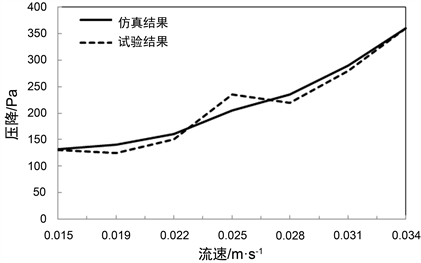
Figure 8. Comparison of resistance properties for filter material between test and simulation results
图8. 滤材阻力特性试验与仿真结果对比
3.2. 空气过滤器阻力特性试验结果
在试验室空气过滤器试验台上,对本次数值模拟的空气过滤器进行了阻力特性试验,试验结果如表4所示。通过表2和表4,得到空气过滤器阻力特性试验与仿真对比曲线,见图9所示。

Table 4. Test results of resistance properties from filter material
表4. 滤材阻力特性试验室结果
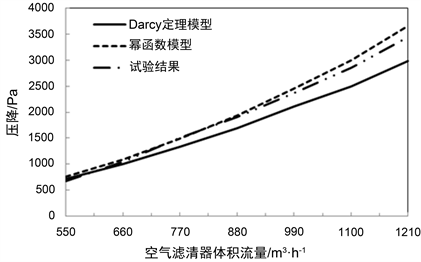
Figure 9. Comparison of resistance properties for air filter between test and simulation results
图9. 空气过滤器阻力特性仿真结果对比
通过空气过滤器阻力特性试验与仿真对比可以看出,2种多孔介质渗透模型对空气过滤器流场的数值模拟都能够达到预期效果。相比而言,采用幂函数模型的结果与试验结果更为接近,由此可以看出,采用滤材仿真结合空气过滤器数值模拟的分析方法,能够得到空气过滤器准确的阻力特性,可以客观模拟出空气过滤器内部流场。
4. 结论
本文利用GeoDict材料分析软件将滤材的电子计算机断层扫描照片生成接近真实结构的三维滤材模型,并进行仿真计算,从而得到滤材的性能数据。以此数据为基础,得到滤材的多孔介质渗透模型。采用多孔介质渗透模型对空气过滤器进行数值模拟,从而得到空气过滤器的阻力特性曲线。通过试验与仿真结果对比,得到以下结论:
1) 由CT照片生成三维模型,能够反映滤材的真实结构,可以进行阻力特性、效率特性等滤材性能的定量分析。
2) GeoDict材料分析软件计算得到的滤材阻力特性能够生成准确的多孔介质渗透模型,可以用于空气过滤器的数值模拟计算。
3) 在空气过滤器数值模拟中,由准确的滤材特性数据建立的幂函数多孔介质渗透模型计算结果更接近试验室结果。
4) 采用GeoDict材料分析软件结合流场分析软件的数值模拟方法能够得到准确、可信的阻力特性,可以指导空气过滤器内流场分析与性能预测。