三维静电场球坐标系曲面边界元法仿真精度分析

Simulation Accuracy Analysis of Surface Boundary Element Method in 3D Electrostatic Field Spherical Coordinate System

摘要: 三维电场的仿真数值计算精度与模型网格的选择和密度有密切关系，相关研究较少，已公开发表的研究成果中数值计算的网格划分大多靠经验，缺少网格剖分规范。基于球坐标系的曲面边界元法以曲面单元离散求解的模型表面，可以减少平面单元的拟合误差。对球面划分不同区域分别进行三角形网格和四边形网格剖分，对不同网格剖分面积和密度进行控制，讨论不同区域网格对仿真计算精度的影响，给出球面模型兼顾计算内存及计算时间下的最佳剖分方法。讨论了不同极点位置对球面积分的影响，结论可以广泛应用于工程实际。

Abstract: The numerical calculation accuracy of the 3D electric field simulation is closely related to the selection and density of the model grid elements. There are few related researches, and most numerical calculations meshes in published research results rely on experience, and there is a lack of mesh selection specifications. The surface boundary element method based on the spherical coordinate system uses the surface elements to discretely solve the model surface, which can reduce the fitting errors of the plane elements. Triangular meshing and quadrilateral meshing are divided into different areas of the spherical surface, and the area and density of different meshes are controlled. The influence of different meshes on the simulation calculation accuracy is discussed. The spherical model is given to take into account the calculation memory and calculation time. The best subdivision method is established. Discussed the influence of different positions of the poles on the area of the ball, the conclusion can be widely used in engineering calculation.

1. 引言

在工程实际中，由于设备仪器及环境的复杂性，分析问题常常需要通过计算机建立仿真模型，利用数值计算的方式对模型进行仿真计算，从而衡量设备仪器是否符合工程标准及故障状态的判断等。

边界元法是工程中求解问题时常用到的数值分析方法之一，区别于需要对全空间进行剖分计算的有限元法，边界元法只需要对模型表面进行剖分计算，大大降低了仿真计算的求解维度和积分点数量，更符合工程实际问题对计算效率和计算内存的要求 [1]。

和有限元法相同，边界元法求解的精度十分依赖于模型网格的剖分情况。边界元法发展早期采用线性插值函数，将模型表面剖分为平面三角形或平面四边形，利用多个平面拟合曲面，在离散的平面单元上进行积分计算 [2] - [12]。由于平面单元与曲面具有一定误差，边界元法积分精度受剖分网格的密度影响，网格越多则平面单元与曲面越接近，误差越小，如图1所示，显然增大网格密度可以更好地拟合曲面减小模型误差。但网格数量增多会增加求解的节点数和单元数，导致计算量和计算内存成倍增加。通过坐标变换，可以实现对模型进行曲面单元剖分，良好地解决平面单元拟合曲面带来的误差 [2] [7] [8]。

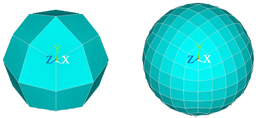
Figure 1. Mesh fitting with different densities

图1. 不同网格密度拟合情况示意图

在已公开的研究成果中，关于静电场的大量数值仿真计算对模型的网格剖分程度仅依靠“经验”，未有详细的网格剖分规范可以参照，显然会无意识地造成计算成本和计算误差的增大。基于球坐标系的曲面边界元法网格剖分对仿真计算精度的研究在目前已公开发表的文献中未有详细体现，由于球模型表面剖分受极点处网格剖分及极轴相对位置的影响，给出球坐标系下曲面边界元法网格剖分的规则对边界元法仿真数值计算的发展和应用有重要指导意义。

2. 球坐标系曲面边界元法积分原理

2.1. 间接边界法

间接边界元法是基于点电荷的基本解和叠加原理的边界元方法 [2] [3] [4] [5] [7] [8] [9] [10]。区域内任意点的电位受边界面电荷影响，面电荷密度σ′(r′)作为源，任意场点的电位φ(r)可以表示为：

$\phi \left(r\right)={\displaystyle \underset{S}{\iint }\frac{\sigma \prime \left(r\prime \right)}{4\pi {\epsilon }_{0}R}dS}$ (1)

式(1)中R是场点与源点的距离，ε₀为真空介电常数。

利用伽辽金加权余量法可以将积分方程离散为代数方程组从而进行数值计算求解，边界积分方程的伽辽金离散形式如式(2)所示。

$\begin{array}{cc}\begin{array}{l}4\pi {\displaystyle \underset{e=1}{\overset{n_e}{\sum }}{\displaystyle \underset{i=1}{\overset{n_p}{\sum }}{\displaystyle \underset{j=1}{\overset{n_p}{\sum }}({\displaystyle \underset{S_e}{\iint }{M}_{m_{e,i}}}{M}_{n_{e,j}}d{S}_e){\phi }_n}}}\\ ={\displaystyle \underset{e=1}{\overset{n_e}{\sum }}{\displaystyle \underset{i=1}{\overset{n_p}{\sum }}{\displaystyle \underset{e^{\prime }=1}{\overset{{n^{\prime }}_e}{\sum }}{\displaystyle \underset{j=1}{\overset{n_p}{\sum }}({\displaystyle \underset{S_{\text{e}}}{\iint }{M}_{m_{e,i}}}{\displaystyle \underset{{S^{\prime }}_e}{\iint }\frac{1}{R}}{M}_{n_{e^{\prime },j}}d{S^{\prime }}_{e}d{S}_e){\lambda }_n}}}}\end{array}& \left(m=1,2,3,\cdots ,n_n\right)\end{array}$ (2)

将φ_n和λ_n写成向量，将上式整理成矩阵相乘的形式为：

$A\left\{\lambda \right\}=B\left\{\phi \right\}$ (3)

其中 $\phi$ 是导体表面的节点电位构成的列向量， $\lambda$ 是σ′/ε₀构成的列向量。

矩阵A、B仅与边界的几何性质有关，单元矩阵可表示为 [7] [8] [9] [10]：

$A_{e,i,e^{\prime },j}={\displaystyle \underset{S_e}{\iint }{N}_i}{\displaystyle \underset{{S^{\prime }}_e}{\iint }\frac{1}{R}}{N}_{j}d{S^{\prime }}_{e}d{S}_e$

$B_{e,i,e,j}={\displaystyle \underset{S_{\text{e}}}{\iint }{N}_i{N}_{j}d{S}_e}$ (4)

式中 $N_i$， $N_j$ 为插值函数，根据上述理论，若已知边界即可求解表面电场的代数方程组。

2.2. 基于球坐标变换的曲面边界元法

直角坐标系下的球面曲面单元可以映射为二维ψ-θ球坐标系下的平面单元，如图2所示。则边界元法对曲面单元的积分计算可以转化为二维平面单元积分计算。

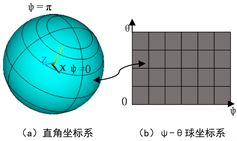
Figure 2. Cartesian coordinate system and spherical coordinate system

图2. 直角坐标系与球坐标系转换关系

直角坐标下点的坐标与ψ-θ球坐标系下坐标转换关系如下：

$y=r_0\sin \theta \sin \phi$, $x=r_0\sin \theta \cos \phi$, $z=r_0\cos \theta$ (5)

式中θ为场点–坐标原点间连线与z坐标轴间夹角， $\theta \in \left[0,\pi \right]$ ；ψ为方位角，即场点–坐标原点间连线与x坐标轴间夹角， $\psi \in \left[0,2\pi \right]$。

可以根据坐标转换关系实现直角坐标系下的曲面四边形的精确积分计算，但由于这种转换关系是基于对球面按照等θ线、等ψ线均匀规则剖分的，由于球表面存在上下两个极点，极点附近无法分割成四边形，因此基于球坐标系变换的曲面边界元法在网格划分时极点处必须划分为曲面三角形网格进行计算。则对球面区域进行分割，划分三角形和四边形剖分范围，讨论其对计算精度的影响对边界元数值仿真计算的发展和应用有重要意义。

3. 球坐标系曲面边界元法精度分析

距离地面无限远处建立半径为1 m的球模型，对其加10 V电压，易知球表面各点电场强度应为10 V/m。对球进行规则三角形剖分，剖分单元数分别为336、1296、5168，剖分5168单元网格图如图3所示，计算结果如表1所示。

Figure 3. 5168-element triangular divided mesh

图3. 5168单元三角形规则剖分网格图

Table 1. Calculation results of triangular mesh

表1. 规则三角形剖分边界元计算结果

由表1可知，随着网格密度增大球体表面场强数值趋于稳定，在同样网格剖分情况下，曲面边界元法精度明显高于平面边界元法，并且随着网格数递减这种高精度优势越明显，因此利用少量的曲面单元替代平面单元，可以达到少网格高精度的目的。

随着网格数量增加，计算时间也明显增加，场强与解析解10 V/m的相对误差逐渐减小，在5168网格数情况下，最大相对误差在百分之七以内，针对单球体在实际工程仿真计算中剖分几千个网格是不现实的，因此在满足精度要求下，尽可能减少剖分网格的数量，提高计算效率是研究仿真数值计算精度的重要目的。

对球体表面进行曲面四边形剖分，由球坐标系转换算法原理可知，球表面的上下极点处需剖分为曲面三角形单元，其余球面规则剖分为曲面四边形单元，三角形单元数为192，总单元数为384，剖分网格如图4所示。将单元和节点数据代入球坐标曲面边界元算法进行数值计算，计算时间为21 s，最大场强数值为10.581 V/m，最小场强数值为9.575 V/m，显然计算结果的最大相对误差在百分之五以内，场强分布云图如图5所示。

Figure 4. 384-element hybrid subdivision mesh

图4. 384单元混合剖分网格图

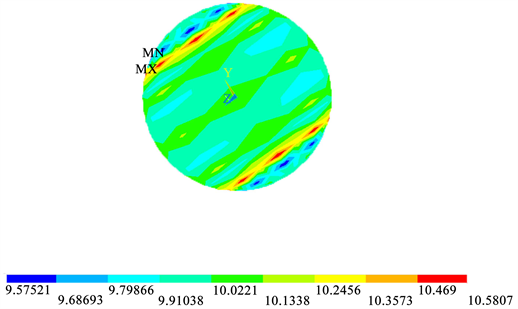
Figure 5. 384-element electric field intensity map

图5. 384单元场强云图

曲面三角形与曲面四边形混合剖分情况下实现了仅384个网格单元就可以达到误差在百分之五以内的仿真计算精度，大大简化了计算内存和计算时间。可以看出曲面四边形单元的积分精度是明显优于三角形单元的，但对于球形模型的表面电场积分计算不可避免极点处三角形网格的剖分，因此讨论极点处网格剖分情况以及多导体间极点位置即极轴的相对方向对仿真计算精度的影响意义重大。

3.1. 极点网格的选择

建立双球模型，球半径为1 m，间距为4 m，电压分别为+10 V、−10 V。以球半径为参照，对球面进行上下对称的不同程度分割。分割线如图6所示，以过球心水平圆周线为基准，由下到上水平分割线分别标记为：L1、L2、L3。L1为距离球心竖直高度0.5 m即半径1/2处圆周线；L2为距离球心竖直高度0.75 m即半径3/4处圆周线；L3为距离球心竖直高度0.875 m即半径7/8处圆周线。

Figure 6. Schematic diagram of dividing line L1-L3

图6. L1-L3分割示意图

根据3条分割线划定不同的球面极点处三角形网格剖分范围，将剖分单元及节点数据代入曲面边界元法进行计算。

以L1及其下方对称线为分割线，对球面分割成三部分，上下包含两极点的曲面用三角形网格剖分，中间曲面用四边形网格剖分，为研究网格密度对精度的影响，在L1为分割线情况下建立5种不同网格密度模型，各模型网格参数如表2所示，各模型计算结果如表3所示。

Table 2. Model parameters in L1

表2. L1分割线下单球面不同密度网格剖分模型参数

Table 3. Calculation results in L1

表3. L1分割线下单球面曲面边界元计算结果

选取规则曲面三角形网格剖分球面，单球面网格数5168的双球模型计算结果作为基准解分析误差。基准解计算时间为40 min，表面总电荷量为1336.497 pC，最大场强值为13.431 V/m，最小场强值为11.145 V/m，单球场强云图如图7所示。

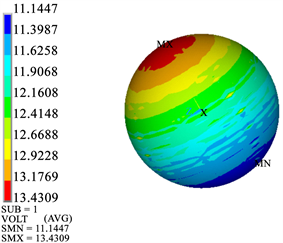
Figure 7. Reference solution electric field cloud map

图7. 基准解电场云图

根据最大场强、最小场强、电荷量计算模型相对误差，结果如图8所示。

Figure 8. Relative error graph

图8. 模型相对误差图

由图8可知，模型1、2三角形网格密度情况相似，四边形网格密度差距近一倍，计算最大相对误差减小近百分之八；模型4、5为四边形剖分情况相同而三角形剖分密度差距近3倍，计算精度差距不大，最大误差均控制在百分之二以内。可得结论，在三角形剖分区域相同的情况下，三角形网格密度对仿真计算结果影响不大，四边形网格密度对计算精度的影响较大。

模型2在三个衡量数值结果中较有优越性，图9为模型2、模型3场强云图。

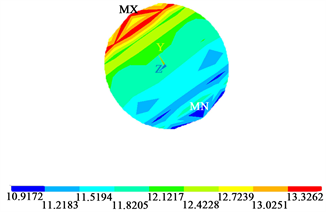(a) 模型2场强云图 (b) 模型3场强云图

Figure 9. Electric field intensity cloud map

图9. 模型2、模型3场强云图

显然模型3场强分布优于模型2，且与基准解场强云图差别较小，模型3的三个最大误差在百分之四以内，保证了误差较小情况下网格数量尽可能减少。

进一步缩小球面三角形单元剖分区域，以L2为分割线，分割方法同L1，将球面分成上中下三个部分，建立不同网格密度模型3个，参数如表4所示，曲面边界元计算结果如表5所示。

Table 4. Model parameters in L2

表4. L2分割线下单球面不同密度网格剖分模型参数

Table 5. Calculation results in L2

表5. L2分割线下单球面曲面边界元计算结果

由表5与表3对比可知，在三角形及四边形网格密度均情况近似的情况下，以L2为分割线划分三角形剖分区域的网格计算结果比以L1为分割线计算结果误差大，且差距明显，尽管缩小了计算时间，但计算误差并未随四边形网格划分区域增大而减小。

进一步缩小球面三角形单元剖分区域，以L3为分割线，分割方法同L1、L2，建立不同网格密度模型2个，参数如表6所示，曲面边界元计算结果如表7所示。

Table 6. Model parameters in L3

表6. L3分割线下单球面不同密度网格剖分模型参数

Table 7. Calculation results in L3

表7. L3分割线下单球面曲面边界元计算结果

对比L3分割下模型2与L1分割下模型3计算结果，在网格密度近似的情况下，L3分割情况下计算时间减少了2 s，但计算误差较L1情况下模型3更大。

因此可以进一步得出结论，球形曲面边界元仿真计算精度受四边形网格影响更大，在四边形剖分区域固定的情况下，网格密度越大计算精度越好；对于整体球面剖分，并非四边形剖分区域越大计算精度越好，取极点到球心方向1/2处圆周为分割线，将球面对称分为上中下三个曲面，上下曲面三角形剖分，中间曲面四边形剖分，计算精度最好。

对于工程实际应用，给出L1分割线下模型3作为球形电极仿真计算网格剖分参考规范，可以保证误差控制在百分之四以内的精度下，计算时间仅30 s左右，相比于边界元和有限元仿真计算节省了10 min以上计算时间及几千的网格数目。

3.2. 极点位置的选择

多个球导体进行电场计算时涉及到每个球表面的网格剖分，则球之间的极点位置选择即极轴间夹角度数对边界元仿真计算是否有影响，在目前已公开的研究中未有涉及。进一步推动边界元算法在工程实际中的应用，需要给出球间极轴夹角对边界元计算的影响。

按照不同极轴夹角及球心与极轴夹角建立三个双球模型如图10所示。

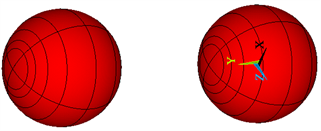(a) 模型1 极轴夹角0度 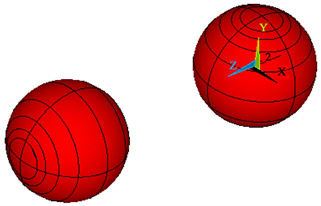(b) 模型2 极轴夹角90度 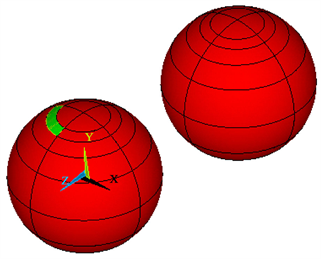(c) 模型2 球心连线与极轴夹角45度

Figure 10. Model diagrams with different angles

图10. 改变角度模型图

由于球体间电容数值与球的相对摆放位置无关，仅与球间距有关，可以利用电容数值作为基准值计算仿真结果的误差。建立图9三个双球模型，假设与地面相距无限远情况下，双球间距4 m，球半径1 m，电压+10 V、−10 V。按照3.1节中给出的网格剖分模型简化计算结果如表8所示。

Table 8. Calculation results of models

表8. 不同模型曲面边界元计算结果

由表8可知，双球系统在三种不同极轴角度下计算结果差距不大，误差在百分之一以内，可以得出结论：静电场球坐标系下曲面边界元数值计算中，对球形电极的网格剖分只与网格的选择和密度有关，与球间极轴相对角度无关，剖分时可以不考虑极点位置选择的影响。

4. 结束语

本文基于网格的选择和密度，对球坐标系下曲面边界元仿真算法精度进行分析，得出球形电极最佳剖分网格模型，在保证了计算精度的情况下大大缩减了计算时间和内存占用。讨论了不同极轴角度对计算精度的影响，得出的仿真计算结论对工程上边界元算法的实际应用具有重要指导意义。