1. 引言
有限元法(FEM)是Rayleigh-Ritz-Galerkin方法与局部紧支分段多项式的结合。有限元法需要生成网格并进行计算 [1] [2]。然而,对于一个工程问题,大约80%的分析时间用于建模和网格生成,只有20%用于计算分析 [3]。因此,有必要提出一些解决这一问题的方法。目前主要有三类方法,一类是无网格法,一类是等几何分析,一类是不匹配网格法。这里主要介绍不匹配网格法中的宽边界法与双宽边界法。
不匹配网格法将求解的物理域放到一个更大的规则的求解域中进行计算,这样便可以使用结构网格对求解域进行离散。
宽边界法(Fat Boundary Method)是一种针对定义在开孔区域上问题的不匹配网格法 [4] [5],它可以在孔周围得到更高精度的解。然而,宽边界法需要一个对应于孔边界条件的解析解 [6] [7]。这就限制了宽边界法的应用范围,因为对于一般的边界条件和孔的形状通常很难得到这样的解析解。
双宽边界法(Dual Fat Boundary Method)是对宽边界法的改进,它不需要计算解析解 [8]。因此,对于定义在开孔区域上的问题,双宽边界法是一种更为通用的方法。
由于宽边界法与双宽边界法都需要迭代求解,在本文中,我们主要研究算法参数如何影响宽边界法的迭代,并提出了一种基于双宽边界法的插值方法以减少计算成本。本文首先对弹性力学开孔问题的宽边界法与双宽边界法作简要介绍,然后介绍基于双宽边界法的插值方法,并通过数值算例对宽边界法迭代的影响因素进行研究,并验证插值方法的精度。最后对研究结论做出总结。
2. 弹性力学宽边界法与双宽边界法
对定义在开孔域(见图1)上的弹性力学问题:
(1)
其中
为位移向量,
为应力向量,
为体力向量。
和
分别表示边界
和
上的位移边界条件。
表示边界
上的力边界条件。
表示
的单位外法线向量。
宽边界法通过引入人为定义的边界
将原问题转化为定义在总体域
与局部域
上的问题:
(2)
其中局部域
的边界为
与
,总体域
表示
与
的并集,即:
。
为变量
在
中的部分。
和
表示变量
和
的延拓,即定义在
上同时在
上为0。方向导数沿着
的外法线方向。
表示在
上为1,其它地方为0的Kronecker δ函数。其中的
为下式的一个解析解:
(3)

Figure 1. FBM and DFBM of elasticity: problem definition
图1. 弹性力学的宽边界法与双宽边界法:问题定义
文献 [9] 给出了方程(1)和方程(2)的等价性的证明。为了对方程(2)进行迭代求解,引入线性算子
:
(4)
其中
及
为下式的解:
(5)
其中
为松弛因子,为了保证收敛,其取值范围为
,常数C为一个与问题相关的常
数。可以使用有限元对方程(5)进行迭代求解。与有限元法相比,宽边界法可以使用结构网格对求解域进行离散,简化了网格生成程序,并且不需要对局部域的细网格与总体域的粗网格之间进行过渡。
从方程(3)中可以看出,宽边界法需要求解变量
,这大大限制了宽边界法的应用范围。对一般形状的孔的边界
或者边界条件
,很难求解方程(3)得到
。为了解决这一问题,Liu等 [8] 提出了双宽边界法。
双宽边界法采用数值方法求解
。该方法引入了另一个人为定义的边界
(见图1)并引入了第三个方程,最终得到双宽边界法基本方程:
(6)
双宽边界法方程(6)可以看作是方程(2)与方程(3)的结合。同时双宽边界法方程(6)也可以采用与宽边界法类似的迭代法进行求解。引入线性算子
:
(7)
其中
、
及
为以下方程的解:
(8)
双宽边界法相当于采用数值的方法求解方程(3),因此该方法不需要解析解,可以在不降低计算精度的前提下大大扩展该方法的应用范围。
3. 基于双宽边界法的差值方法
双宽边界法引入第三个方程并与其它两个方程采用相同的离散方法进行求解,这大大增加了计算成本。因此这里提出一种插值的方法,避免求解方程(8).III。
从方程(8)可以看出,方程(8).III没有物理意并且其主要作用就是计算
。因此对于一些较简单的问题,采用有限元对
进行离散后,节点位移可以直接从总体域
的结果插值得到,而不用通过有限元进行求解得到。从下面的数值算例中可以看出采用插值的方法对计算精度并没有太大的影响。
4. 数值算例
这里计算两个数值算例,第一个算例为孔边固定的开孔板的单轴拉伸问题,第二个算例为孔边径向位移的开孔板问题。两个算例分别使用宽边界法与双宽边界法求解。局部域在第m次迭代的误差定义为:
(9)
其中带有上标
的变量表示解析解。第m次迭代与第m + 1次迭代之间的相对误差定义为:
(10)
4.1. 孔边固定的开孔板的单轴拉伸问题
第一个算例计算孔边固定的开孔板的单轴拉伸问题,如图2所示。宽边界法的网格如图3所示。边界
的半径为0.6。该问题的位移解为 [10]:
(11)
其中对平面应力问题
。
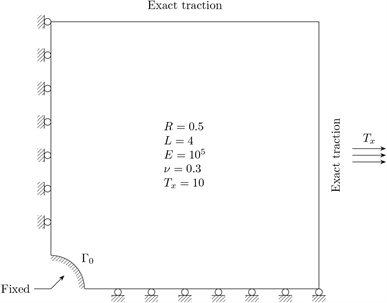
Figure 2. Perforated plate with a fixed hole
图2. 孔边固定的开孔板
迭代初始值设为零,即总体域
的初始位移为零。对于不同单元数量的迭代误差如图4所示。其中
表示总体域在x方向的单元数量,并且总体域y方向的单元数量与之相等,即:
。局部域径向的单元数量等于
,环向的单元数量设置为使得局部域的单元尽可能接近正方形。
从图4可以看出,采用不同单元数量对求解域进行离散,宽边界法都能够快速地收敛。并且随着单元数量的增加,能够收敛到更高精度的解。
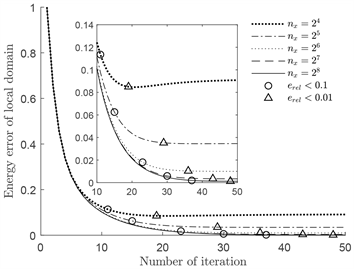
Figure 4. Iteration errors for different meshes
图4. 不同网格的迭代误差
总体域在局部域重合部分的误差与局部域的误差的对比如图5。从图中可以看出,局部域的误差远远小于总体域在局部域重合部分的误差。实际上,这些误差最大相差两个数量级,如图6所示。

Figure 5. Displacement error of global domain and local domain
图5. 总体域与局部域的位移误差

Figure 6. Comparison of errors of global domain and local domain
图6. 总体域与局部域的误差对比
从图7可以看出,对比宽边界法与有限元法,达到同样的计算精度,宽边界法使用的单元数量更少。同时,宽边界法可以使用结构网格对求解域进行离散,简化了网格生成程序,尽量避免了网格畸变的情况。

Figure 7. Comparison of element numbers of FBM and FEM
图7. 宽边界法与有限元法单元数量对比
除了单元数量,宽边界法的初始化也影响迭代次数。将总体域的位移初始化为
之间的随机数,其中n从0变化到−7。从图8可以看出初始值的误差越大,所需的迭代次数越多。同时,迭代次数与初始值误差的对数基本呈线性关系。因此零初始化是一种比较合适的方式,所需的迭代次数不多。
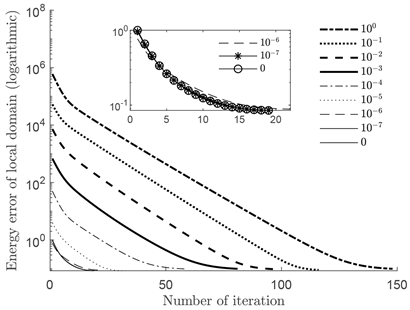
Figure 8. Iteration errors for different initializations
图8. 不同初始化的迭代误差
4.2. 孔边径向位移的开孔板问题
该算例的开孔板受到孔边
径向位移的作用,如图9所示。位移的值
,该问题的位移解为:
(12)
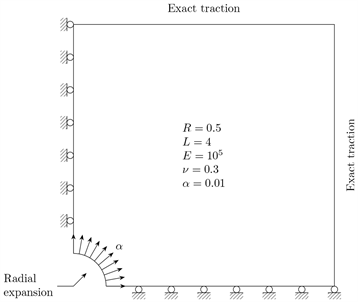
Figure 9. Perforated plate with a expanded hole
图9. 孔边径向位移的开孔板问题
使用双宽边界法求解该算例。与宽边界法不同,双宽边界法需要对局部域
进行网格划分。根据第3章的描述,这里在单元划分后采用插值的方法得到节点的位移。同时,与局部域
相比,局部域
可以采用相对粗糙的网格进行离散,如图10所示。
从图11中可以看出,对局部域
使用较少的单元同样可以达到相同的精度。
改变单元数量和初始化数值,我们可以得到与宽边界法相同的结论。总体域在局部域重合部分的误差与局部域的误差对比如图12所示。从图中可以看出,局部域的误差远远小于总体域的误差。实际上,这些误差最大相差两个数量级,如图13所示。
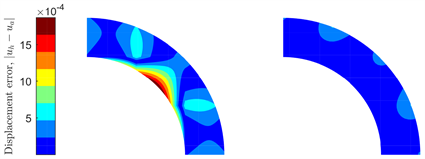
Figure 12. Displacement error of global domain and local domain
图12. 总体域与局部域的位移误差

Figure 13. Comparison of errors of global domain and local domain
图13. 总体域与局部域的误差对比
5. 结论
宽边界法与双宽边界法作为不匹配网格方法,可以使用结构网格对计算域进行离散,与有限元法相比,宽边界法与双宽边界法可以使用更少的单元在孔周围得到相同的计算精度。数值算例表明,宽边界法对算法的初始化不敏感,即对任意的初始化都能够收敛,但初始化的误差越大,所需的迭代次数越多。一般情况下,使用零初始化即可尽量降低迭代次数。同时,对双宽边界法的算例表明,由于孔内位移沿孔的半径方向线性分布,因此直接利用总体域的结果对孔内局部域的位移进行插值即可,无需对孔内局部域进行有限元求解。然而对更一般的问题,需要研究更高精度的插值方法,这也是进一步研究的方向。
致谢
作者非常感谢编辑和匿名审稿人的深刻意见和建议。
NOTES
*通讯作者。