一种基于属性显著度的实体解析算法

doi:10.12677/HJDM.2021.112004

期刊菜单

一种基于属性显著度的实体解析算法
An Entity Resolution Algorithm Based on Attribute Salience

DOI: 10.12677/HJDM.2021.112004, PDF, HTML, XML, 被引量下载: 497 浏览: 1,133
作者: 褚良旭, 李贵, 李征宇, 韩子扬, 曹科研：沈阳建筑大学，信息与控制工程学院，辽宁沈阳
关键词: 实体解析；属性显著度；二部图；随机游走；Entity Resolution； Attribute Salience； Bipartite Graph； Random Walk

摘要: 实体解析(ER)是数据集成和数据清洗的一个重要步骤。在领域数据清洗与集成中，实体中不同的属性通常能表现出不同的区分能力，计算并利用属性的区分能力能够提高记录相似度的精确度。目前实体解析的方法有采用基于字符串的记录相似度算法以及基于机器学习的算法等方法来计算记录相似度，缺少考虑不同属性的重要程度。因此本文利用SimRank和PageRank算法的思想并结合随机抽样得到的属性显著度提出了一种基于属性显著度的计算记录相似度算法。首先，构造一个加权的属性记录对二部图来表示属性与记录对之间的关系；其次，根据属性显著度结合图论相似度算法提出了基于属性显著度的计算记录相似度的迭代算法。最后，构造一个记录图来表示记录对之间的匹配概率(二部图中的权值 w（r_i,r_j）)，并使用改进的随机游走算法估计记录对匹配的概率。再将记录对的匹配概率反馈给加权的属性记录对二部图，并对基于属性显著度的计算记录相似度算法中的权值w（r_i,r_j）进行修正，直到收敛。利用房地产领域数据集进行了实验评估，结果表明，本文提出的基于属性显著度的实体解析算法与主流方法相比，具有较高的精确度。

Abstract: Entity resolution (ER) is an important step in data integration and data cleansing. In domain data cleaning and integration, different attributes in an entity usually exhibit different discriminating abilities. Calculating and utilizing the discriminating abilities of attributes can improve the accuracy of record similarity. Current entity resolution methods include record similarity algorithm based on string and algorithm based on machine learning to calculate record similarity, which lacks the im-portance of considering different attributes. Therefore, this paper uses the idea of SimRank and PageRank algorithm and combines the attribute salience obtained by random sampling to propose a similarity algorithm based on attribute salience. Firstly, a weighted attribute record pair bipartite graph is constructed to represent the relationship between attribute and record pair. Secondly, an iterative algorithm for calculating record similarity based on attribute significance is proposed ac-cording to attribute significance combined with graph similarity algorithm. Finally, a record graph is constructed to represent the matching probability between the record pairs (the weight in the bipartite graph), and the improved random walk algorithm is used to estimate the matching probability of the record pairs. Then, the matching probability of record pairs is fed back to the weighted bipartite graph of attribute record pairs, and the weight in the algorithm of calculating record similarity based on attribute salience is modified until convergence. Experi-mental evaluation using real estate data sets shows that the proposed entity resolution algorithm based on attribute salience is more accurate than the mainstream methods.

文章引用：褚良旭, 李贵, 李征宇, 韩子扬, 曹科研. 一种基于属性显著度的实体解析算法[J]. 数据挖掘, 2021, 11(2): 27-37. https://doi.org/10.12677/HJDM.2021.112004

1. 引言

实体解析是识别数据集中指向同一实体的记录 [1]。相似度算法是实体解析的核心和基础。早期的研究工作提出了各种基于字符串距离函数来度量记录对之间的相似度。例如基于字符串的 [2] 或基于标记的相似度算法 [3] [4]。基于字符串相似度的方法，包括Jaccard和TF-IDF，是一种高效、易于实现的方法。例如，Paul Jaccard [5] 提出的Jaccard相似度算法，是一种最常见的评判实体记录相似程度的统计指标。文献 [6] 中提出了TF-IDF距离度量来计算记录相似度。这些算法它们的识别精确度不够高。

为了克服基于距离的方法的精确度不高的问题，随着机器学习的快速发展，基于机器学习的实体解析方法开始流行起来 [7]：采用机器学习的方法学习字符串编辑距离度量参数 [8] [9]，或者结合不同距离度量的方法来提高精确度 [10] [11]。例如，在 [12] 中，将实体解析建模为分类任务，并用SVM进行求解。但采用监督机器学习技术的一个前提是需要大量的训练实例。这需要大量的人工开销；此外，非匹配记录对的数量远远超过匹配记录对的数量，这也给训练数据集的准备带来了挑战。

此外，在不同领域数据集中，属性通常能表现出不同的区分能力 [13] [14]。例如，在表1中区分房地产楼盘信息时，楼盘名称与地址的属性更有辨别力。因此可以考虑利用属性的显著度(区分能力)来提高记录相似度算法的精确度。本文通过属性显著度结合适当的记录相似度算法思想提出了基于属性显著度的记录相似度迭代算法。本文的主要贡献如下：

1) 通过构造一个属性–记录对二部图来建模属性和记录对之间的所属关系。

2) 提出一种基于属性显著度的记录相似性迭代算法，来计算记录对的相似度。

3) 利用记录图来计算记录对之间某一属性的匹配概率。并通过改进的随机游走算法来估算记录图中边的权值(匹配概率)。

4) 在地产领域数据集上进行了实验，验证了算法的有效性。

Table 1. Data information table

表1. 数据信息表

本文的结构组织如下。本文在第2节介绍了基于SimRank和PageRank的相似度算法相关理论，在第3节给出了基于属性显著度的记录相似性迭代算法，第4节给出了基于记录图的改进随机游走算法来计算迭代算法中的权值 $w (r_{i}, r_{j})$ ，最后在第5节对算法进行实验验证，第6节进行了总结。

2. 基于图论的相似度算法

基于图论的相似度算法在推荐系统中广泛使用。PageRank [15] 和SimRank [16] 是其中两个最具代表性的图论算法。同样也可以将PageRank和SimRank算法用来解决实体解析中记录的相似度问题 [17]，下面将介绍两种图论算法在实体解析中的应用。

2.1. 基于SimRank相似度算法的相关理论

在推荐系统中，如果A和B两个人购买的项目集O(A)和O(B)相似，则他们两个人的购买兴趣是相似的。这是SimRank在推荐系统中的判定相似度的基本思想。在文献 [16] 中提出了基于二部图的SimRank模型，用来估计推荐系统中两个用户之间的相似度。如图1(a)所示，同样可以在记录 $r_{i}$ 和术语(属性值中的关键词) $t_{i}$ 之间构造一个二部图，来计算记录之间的相似度，计算记录相似度 $S_{b} (r_{i}, r_{j})$ 公式如下：

$S_{b} (r_{i}, r_{j}) = \frac{C_{1}}{| O (r_{i}) | | O (r_{j}) |} \sum_{t_{i} \in O (r_{i})} \sum_{t_{j} \in O (r_{j})} S_{b} (t_{i}, t_{j})$ (1)

其中 $C_{1}$ 为衰减因子， $O (r_{i})$ 为记录 $r_{i}$ 的出邻居， $S_{b} (t_{i}, t_{j})$ 为两个术语 $t_{i}$ 和 $t_{j}$ 之间的相似度评分，可以用相同的递归方式定义：

$S_{b} (t_{i}, t_{j}) = \frac{C_{2}}{| I (t_{i}) | | I (t_{j}) |} \sum_{r_{i} \in I (t_{i})} \sum_{t_{j} \in I (t_{j})} S_{b} (r_{i}, r_{j})$ (2)

其中 $C_{2}$ 也是一个衰减因子，而 $I (t_{i})$ 为记录 $t_{i}$ 的入邻居。最后，可以通过迭代这两个方程可以得到记录对之间的相似度。如果两个记录的相似度 $S_{b} (r_{i}, r_{j})$ 超过预定义的阈值，则可以说它们指向同一实体。

2.2. 基于PageRank相似度算法的相关理论

同样，用于推荐系统的PageRank也可以在实体解析中应用，一种方法是用图论方法代替TF-IDF (term frequency-inverse document frequency)项权重策略，推导出一种新的文本相似性度量。Mihalcea与Tarau提出的TextRank，其思想非常简单：通过词之间的相邻关系构建网络，然后用PageRank迭代计算每个节点的rank值，排序rank值即可得到关键词。在实体解析应用中，TextRank构造一个无向术语图，如图1(b)所示，其节点是术语，而边对应于文档中固定大小滑动窗口中两个术语的共同出现。在此基础上，应用基于PageRank的文本浏览模型估计了该词在该领域的重要性。同样的图形模型也可以用于的TW-IDF (term weight-inverse document frequency)。

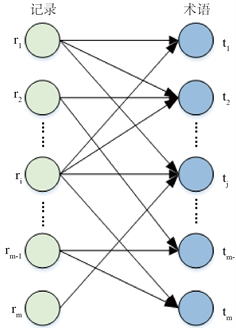(a) 二分图 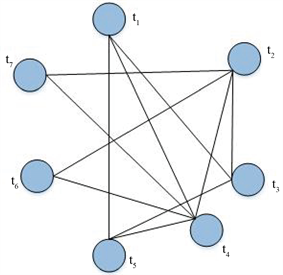(b) 统一图

Figure 1. Graph models in graph-theoretic

图1. 图论中的图模型

本文的第二个基准算法采用TW-IDF作为一种新的文本相似性度量，它将每个文本记录作为文档中的一个段落，并构造相关的术语图。术语 $t_{i}$ 的显著性是由公式(3)表示

$S (t_{i}) = (1 - φ) + φ \sum_{t_{i} \in N (r_{i})} \frac{s (t_{j})}{| N (t_{i}) |}$ (3)

$φ$ 是阻尼因子通常设置为0.85， $N (t_{i})$ 表示相邻项无向图。两条记录之间基于TW-IDF的文本相似度 $S_{u} (r_{i}, r_{j})$ 由它们共同术语的权重和公式(4)来表示：

$S_{u} (r_{i}, r_{j}) = \sum_{t \in r_{i} \land t \in r_{j}} s (t) \cdot \log \frac{n + 1}{d f (t)}$ (4)

其中n为数据集中记录的总数， $d f (t)$ 为包含t的记录的总数。如果两个记录不具有相同的属性，则将它们的相似性为0，通过定义适当的阈值，如果它们的文本相似性超过这个阈值，我们考虑两个记录指向同一实体。

3. 基于属性显著度的记录相似度算法

在本节，本文提出了一种基于属性显著度的计算记录相似度算法。首先，定义一个基于属性显著度度的记录相似度算法，然后通过构造一个二部图来建模属性与记录对之间的关系。最后，详细介绍了基于二部图的属性显著度的迭代算法，该算法同时估计了实体解析中记录对的相似度和属性的显著度。

3.1. 基于属性显著度的相似度

传统的TF-IDF方法对文档(记录)中的频繁项赋予较高的权重，并使用逆文档频率因子对常见或禁用词进行惩罚。类似地，TW-IDF度量也更喜欢记录语料库中的频繁词汇，因为它们将与滑动窗口中的许多其他词汇同时出现，并在术语图中充当中心。然而，在确定匹配记录对时非常重要的判别项可能没有很高的TF分数。例如，楼盘数据集中的频繁属性详细地址，可能在一条记录中只出现一次，但是它们在判断两个楼盘是否是同一个时具有很高的区分度。虽然TF-IDF或TW-IDF中的IDF因子也有助于提高这些属性的权重。但是IDF是一种通用的度量方法，无法区分数据集中真正有区别的属性和低频噪声属性。

本文提出了一种基于属性显著度的相似度算法。它首先通过小样本数据集估计每个属性的显著度:在相似的记录对中计算某些属性值匹配个数占总体匹配数的比例，其值越高意味着这些匹配对记录对相似的贡献度就越大；对应地，在不匹配的记录中计算某些属性值匹配的个数占总体不匹配数的比例，其值越高意味着这些属性对匹配的贡献度越低，进而用以惩罚这些属性的贡献度，最后，两者共同确定属性显著度。

定义1. 属性正证据：在相似的记录对中计算某些属性值匹配个数占总体匹配数的比例，其值越高意味着这些匹配对记录对相似的贡献度就越大。

$P S_{A_{m}} = \frac{| {(r_{i}, r_{j}) | r_{i} \approx_{σ} r_{j}, A_{m} (r_{i}) \approx_{θ_{A_{m}}} A_{m} (r_{j})} |}{| {(r_{i}, r_{j}) | r_{i} \approx_{σ} r_{j}} |}, 0 < m < M, 0 < i \neq j < N$ (5)

其中分子 $| {(r_{i}, r_{j}) | r_{i} \approx_{σ} r_{j}, A_{m} (r_{i}) \approx_{θ_{A_{m}}} A_{m} (r_{j})} |$ 表示达到相似度阈值 $σ$ (达到即为匹配)的记录中，某个属性

的匹配个数，分母 $| {(r_{i}, r_{j}) | r_{i} \approx_{σ} r_{j}} |$ 表示达到相似度阈值 $σ$ 的记录对个数(即匹配个数)。

定义2. 属性负证据：在不匹配的记录中计算某些属性值匹配的个数占总体不匹配数的比例，其值越高意味着这些属性对匹配的贡献度越低，进而用以惩罚这些属性的贡献度。

$N S_{A_{m}} = \frac{| {(r_{i}, r_{j}) | r_{i} \neq_{τ} r_{j}, A_{m} (r_{i}) \approx_{θ_{A_{m}}} A_{m} (r_{j})} |}{| {(r_{i}, r_{j}) | r_{i} \neq_{τ} r_{j}, \exists A_{n} A_{n} (r_{i}) \approx_{θ_{A_{n}}} A_{n} (r_{j})} |}, 0 < i \neq j < N, 0 < m, n < M$ (6)

其中分子 $| {(r_{i}, r_{j}) | r_{i} \neq_{τ} r_{j}, A_{m} (r_{i}) \approx_{θ_{A_{m}}} A_{m} (r_{j})} |$ 表示低于阈值 $τ$ (低于即不匹配)的记录中，某个属性匹配的个数，分母 $| {(r_{i}, r_{j}) | r_{i} \neq_{τ} r_{j}, \exists A_{n} A_{n} (r_{i}) \approx_{θ_{A_{n}}} A_{n} (r_{j})} |$ 所有低于阈值 $τ$ (即不匹配)的记录对。

那么单个属性综合显著度公式可以表示如下：

$S_{A_{m}} = P S_{A_{m}} - N S_{A_{m}}$ (7)

为解决 $P S_{A_{m}}, N S_{A_{m}}$ 可能不在同一量纲上的问题，可表示为

$S_{A_{m}} = P S_{A_{m}} \cdot (1 - N S_{A_{m}})$ (8)

然后通过将显著度公式与基于图论的公式相结合，形成了本文的基于属性显著度的相似度算法。本文以递归的方式定义了属性综合权重 $A S_{t}$ 和记录相似度 $s (r_{i}, r_{j})$ ：

$A S_{t} = S_{A_{m}} \sum_{i \neq j} w (r_{i}, r_{j}) s (r_{i}, r_{j}) s (A_{m} (r_{i}), A_{m} (r_{j}))$ (9)

$S (r_{i}, r_{j}) = \sum_{i \neq j, t \in r_{i} \land t \in r_{j}} s (A_{m} (r_{i}), A_{m} (r_{j})) * A S_{t}$ (10)

其中 $w (r_{i}, r_{j})$ 表示 $r_{i}$ 和 $r_{j}$ 指向相同实体的概率( $i \neq j$ )。将其初始化为1。在公式(9)中，如果共享该属性的所有记录对都指向同一个实体，则将高权重 ${S^{'}}_{A_{m}}$ 赋给该属性。换句话说，这些配对同时具有高相似度 $S (r_{i}, r_{j})$ 和高匹配置信度 $w (r_{i}, r_{j})$ 。 $S_{A_{m}}$ 是一个随机采样的属性显著度的样本值，其值用于惩罚不具有区分性的频繁共享属性。 $s (A_{m} (r_{i}), A_{m} (r_{j}))$ 为 $r_{i}$ 和 $r_{j}$ 的某一属性的属性值相似度。随着公式(9)的收敛， $A S_{t}$ 为修正后的记录综合属性显著度(属性综合权重)。递归式(10)中的记录相似度 $S (r_{i}, r_{j})$ 被直接定义为同一属性的属性显著度和其属性值相似度乘积的和，值得范围在(0,1)之间。根据定义，如果 $r_{i}$ 和 $r_{j}$ 不共享任何属性，则 $S (r_{i}, r_{j})$ 被设为0。本文接下来用改进的二部图表示属性和记录对之间的关系。

3.2. 构造属性–记录对之间关系的二部图

属性和记录对之间的关系可以通过二部图来表示。如图2表示了二部图 $G (R, W, T)$ 的一个示例，其中有两种类型的节点：一种是属性值(术语)节点集T，表示记录对中包含的属性；另一种是记录对节点集R，表示一对记录。属性值节点集T和记录对节点集R通过加权边集W来相连。设t为属性值节点， $(r_{i}, r_{j})$ 为记录对节点。当属性值t同时出现在 $r_{i}$ 和 $r_{j}$ 记录中时，节点和 $(r_{i}, r_{j})$ 才相连。如果一对 $(r_{i}, r_{j})$ 没有共享任何属性节点，则可以认为这对记录不匹配，并将其排除在二部图之外。本文为每个节点都设置了一个权重参数。对于属性值节点t，其权值 $A S_{t}$ 表示其对实体的识别能力，即属性显著度;对于一个记录对节点 $(r_{i}, r_{j})$ ，其权值 $s (r_{i}, r_{j})$ 表示对应记录对的相似度—— $S (r_{i}, r_{j})$ 越大， $(r_{i}, r_{j})$ 表示同一实体的可能性越

属性值节点集T和记录对节点集R通过加权边集W来相连。权值 $w (t_{i}, t_{j}) \in W$ 是 $r_{i}$ 与 $r_{j}$ 之间的匹配概率。本文在下节通过随机游走算法来估计两个记录的匹配概率 $w (r_{i}, r_{j})$ 。它控制从记录对节点转移到属性节点的权重。如果两个记录 $r_{i}$ 和 $r_{j}$ 不匹配，那么我们认为它们的共享属性值节点没有为这对记录的相似度做出贡献。

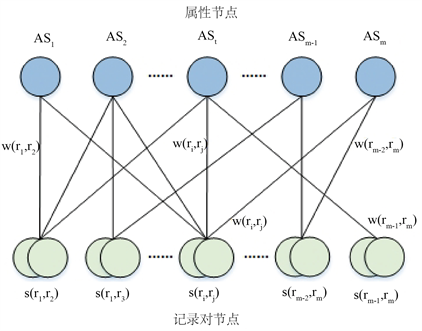
Figure 2. Bipartite graph for attributes and record-pairs

图2. 记录对–属性二分图

3.3. 基于二部图的属性显著度的迭代算法

本文提出的基于二部图的属性显著度的迭代算法综合了SimRank公式(1)、公式(2)和PageRank公式(3)、公式(4)的优点，并具有以下特点：

1) 本文用 $S_{A_{m}}$ 来惩罚属性显著度不高的频繁属性。即公式(8)。

2) 本文构造了一个加权的属性–记录二部图，来估计两个记录指向同一实体的概率 $w (r_{i}, r_{j})$ 。即公式(9)。

3) 本文还通过基于记录图的随机游走算法来估计加权二部图的权值(详见第4节)。

上述的算法1首先：

1) 在(0, 1)随机初始化 $A S_{t}$ (算法第1行)。

2) 如果 $s_{t}$ 不收敛，则对记录对 $(r_{i}, r_{j})$ ，他的相似度 $s (r_{i}, r_{j}) = \sum_{t \in r_{i} \land t \in r_{j}} A S_{t}$ 进行循环(2~4行)。

3) 将 $s (r_{i}, r_{j})$ 输入回 $A S_{t}$ 循环并标准化 $A S_{t}$ (5~7)，如此迭代，直到收敛。

4. 基于随机游走的二部图边权值计算

本文与图论相似度算法的第二个不同便是通过随机游走算法来估计二部图的加权边 $w (r_{i}, r_{j})$ 。随机游走得到的记录对匹配概率可以输入回迭代公式(9)，作为二部图的边权值，来提高记录相似的精确度。在本节中，先介绍随机游走产生权值的朴素算法 [17]，然后基于构造的记录图，提出了基于记录图的改进随机游走算法，估计记录对的匹配概率。

4.1. 朴素随机游走算法

在算法2中介绍朴素随机游走算法：

1) 模拟M次随机游走，其中一半从 $r_{i}$ 开始，另一半从 $r_{j}$ 开始。

2) 估计 $r_{i}$ 到达 $r_{j}$ 的概率和 $r_{i}$ 到达 $r_{j}$ 的概率(第3~7行)。每一次随机游走输出数字1或0，表示冲浪者是否在给定的S步骤内到达目标节点。

3) 然后将成功到达目标的游走的百分比作为匹配概率 $w (r_{i}, r_{j})$ 的值(第8行)。如果 $(r_{i}, r_{j})$ 是匹配对，那么到达概率应接近1。

之所以考虑 $(r_{i}, r_{j})$ 边的两个方向随机游走，是因为分别自 $r_{i}$ 和 $r_{j}$ 的到达概率可能不相同。一个极端的例子是一个节点只有一个邻节点，这样的话，这个节点总是会到达目标，因为没有其他选择。采用双向随机游走就可以抑制这种极端情况。

4.2. 构造记录图

本文构建记录图Gr，它的每个节点表示一个记录，边权重表示两个相连接的记录的相似度。同时构建“参考标准”记录图Gopt，当且仅当它们指向同一实体时才连接两个记录(团属性)。显然，对于Gopt，代表相同实体的记录形成一个与Gopt的其余部分断开连接的团。本文利用Gr的拓扑结构，将其转换为Gopt。为了解决图规约问题，本文利用Gopt了的团属性结构：理想情况下，如果记录 $r_{i}$ 和 $r_{j}$ 指的是不同的实体，则它们应该位于不同的团中，这些团彼此之间是不可达的。相反，如果 $r_{i}$ 和 $r_{j}$ 指的是同一个实体，它们应该在同一个团中并且可以相互访问；也就是说，如果从一个记录 $r_{i}$ 开始随机游走，则很可能通过改进的随机游走算法在一定步骤内访问另一个记录 $r_{j}$ 。通过构造的记录图，本文将随机游走算法进行了改进，改进的算法见4.3。

4.3. 改进的随机游走算法

本文把从记录 $r_{i}$ 到记录 $r_{j}$ 的到达概率作为匹配概率 $w (r_{i}, r_{j})$ 。如果两个记录指向同一个实体，则到达的概率接近1.否则概率将接近0。传统的随机游走由于采用边之间的线性转移概率而不能满足要求。此外如果游走的步数很大，则运行时间会急剧增加，并且会有许多到达概率接近1的非匹配对.如果游走的步数很小，就可能会获得非常少的匹配对，这被认为是假阴性。

为了解决这个问题，采取保护高相似度得分的边，将转移概率设计为边权值的非线性变换：

$w (r_{i}, r_{j}) = \frac{{(1 + β)}^{α} s {(r_{i}, r_{j})}^{α}}{\sum_{r_{j} \in O (r_{i})} s {(r_{i}, r_{j})}^{α}}$ (11)

其中 $w (r_{i}, r_{j})$ 为 $r_{i}$ 到 $r_{j}$ 的概率， $O (r_{i})$ 表示记录图中 $r_{i}$ 的邻域， $α$ 是一个可调参数， $α$ 越大，就越有可能选择较高的权重的边。本文在下面的实验中将 $α$ 设置为25来加大挑选匹配记录作为下一个节点和挑选不匹配节点的之间的可能性。利用修正的转移概率，即使经过多次随机游走，两个不匹配记录之间的到达概率仍然非常小。 $β$ 是一个加权参数， $β \in (0, 1)$ ，用来加权最可能匹配的边。通过改进的随机游走算法，我们就可以利用到达概率来估计匹配概率。

算法3描述了基于属性记录伴随图改进的随机游走算法。首先给定一个权值因子 $β$ 和一个参数 $α$ 。 $β$ 是一个(0, 1)之间的随机值，用于加强权值最大的边， $α$ 是一个足够大的参数，使权值较高的边能够脱颖而出。接下来是随机游走。如果到达目标节点，则返回1，如果在10次之内，还没有到达目标节点，则返回0。

5. 实验

5.1. 数据集

本文用Python对“面向房地产领域的Web数据抽取”项目所抽取的多个数据源的楼盘、楼栋和户数据表数据集进行实验，经过数据清洗、无用数据删除两个预处理过程。对于数据预处理，首先标记文本内容，然后删除了非常频繁的属性。这一步是自然语言处理中常见的做法。这些频繁的属性可能会冲淡区别属性的影响，消除他们可以在一定程度上提高准确率。

5.2. 方法比较

为了进行算法评估，本文采用四种实体解析方法进行实验，将提出的基于属性显著度的记录相似度算法与5个相似度算法进行了比较，包括基于字符串距离的、基于机器学习的和基于图论的基础算法。具体算法如表2所示。

对于基于字符串的相似性方法(Jaccard和TF-IDF)，需要一个合适的阈值来确定匹配对。根据领域需求相似度阈值为0.80。

在基于图论的相似度算法中，本文将二分图上SimRank的C1和C2设置为0.8。对于PageRank的词图,阻尼系数为0.85。

Table 2. Comparing algorithms

表2. 对比算法

5.3. 实验结果及分析

本文采用精确度(precision)、召回率(recall)、F1-score，对实验结果进行评估分析。精确度(precision)是分块正确的正例数量占所有分为正例的百分比，召回率(recall)是分块正确的正例数量占实际正例数量的百分比，F1-score是它们的调和均值。

基于字符串相似性的方法，包括Jaccard和TF-IDF，是一种高效、易于实现的方法。然而，它们的识别精度不够高，两者中TF-IDF在数据集中获得了较高的f1值，因为idf赋予了特征项更高的权重。监督机器学习方法显著提高了精度，但效率有限。此外，他们需要相当数量的标记数据进行监督训练。基于图论的算法结果并不理想，因为SimRank只利用了记录和术语(属性值)之间的结构联系；PageRank只考虑了基于术语(属性值)的相似性。如图3在实验数据集中本文提出的相似度算法与5种算法相比，在精确率、召回率以及F1-score上相媲美，甚至更高。

Figure 3. Experimental result

图3. 实验结果

6. 结论

本文提出了一种基于属性显著度的记录相似度计算算法，在此基础上，采用随机游走算法来估计记录的匹配概率。最后在地产数据集上进行了实验，实验结果验证了算法的有效性。实验结果表明其精确度，召回率，F1-score可以与传统方法和现在主流的方法相媲美，甚至更高。

参考文献

[1]	Christophides, V., Efthymiou, V. and Stefanidis, K. (2015) Entity Resolution in the Web of Data: Synthesis Lectures on the Semantic Web: Theory and Technology. Morgan & Claypool Publishers. https://doi.org/10.2200/S00655ED1V01Y201507WBE013
[2]	韦海浪, 李贵, 李征宇, 韩子扬, 曹科研. 半结构化实体解析算法[J]. 数据挖掘, 2020, 10(1): 1-15. https://doi.org/10.12677/HJDM.2020.101001
[3]	Kenig, B. and Gal, A. (2013) MFIBlocks: An Effective Block-ing Algorithm for Entity Resolution. Information Systems, 38, 908-926. https://doi.org/10.1016/j.is.2012.11.008
[4]	Kolb, L., Thor, A. and Rahm, E. (2012) Dedoop: Efficient Deduplica-tion with Hadoop. Proceedings of the VLDB Endowment, 5, 1878-1881. https://doi.org/10.14778/2367502.2367527
[5]	高广尚, 张智雄. 关于实体解析基本方法的研究和述评[J]. 数据分析与知识发现, 2019, 3(5): 27-40.
[6]	Bilenko, M. and Mooney, R.J. (2003) Adaptive Duplicate Detection Using Learnable String Similarity Measures. Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington DC, August 2003, 39-48. https://doi.org/10.1145/956750.956759
[7]	Cohen, W.W. (2000) Data Integration Using Similarity Joins and a Word-Based Information Representation Language. Information Systems, 18, 288-321. https://doi.org/10.1145/352595.352598
[8]	Ristad, E. S. and Yianilos, P.N. (1998) Learning String-Edit Distance. IEEE Transactions on Pattern Analysis and Machine Intelligence, 20, 522-532. https://doi.org/10.1109/34.682181
[9]	Bilenko, M. and Mooney, R.J. (2002) Learning to Combine Trained Dis-tance Metrics for Duplicate Detection in Databases. TechRep AI, 02-296.
[10]	Tejada, S., Knoblock, C.A. and Minton, S. (2001) Learning Object Identification Rules for Information Integration. Information Systems, 26, 607-633. https://doi.org/10.1016/S0306-4379(01)00042-4
[11]	Cohen, W.W. and Richman, J. (2002) Learning to Match and Cluster Large High-Dimensional Data Sets for Data Integration. Proceedings of the 8th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, July 2002, 475-480. https://doi.org/10.1145/775047.775116
[12]	Ravikumar, P.D. and Cohen, W.W. (2004) A Hierarchical Graphical Model for Record Linkage. Proceedings of the 20th Conference on Uncertainty in Artificial Intelligence, 454-461.
[13]	张晓辉, 蒋海华, 邸瑞华. 基于属性权重的链接数据共指关系构建[J]. 计算机科学, 2013, 40(2): 40-43.
[14]	强保花, 吴忠福. 基于属性信息熵的实体匹配方法研究[J]. 计算机工程, 2005, 31(21): 31-33.
[15]	Brin, S. and Page, L. (2002) The Anatomy of a Large-Scale Hypertextual web Search Engine. Computer Networks and ISDN Systems, 30, 107-117. https://doi.org/10.1016/S0169-7552(98)00110-X
[16]	Jeh, G. and Widom, J. (2002) Simrank: A Meas-ure of Structural-Context Similarity. KDD’02: Proceedings of the 8th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, July 2002, 538-543. https://doi.org/10.1145/775047.775126
[17]	Zhang, D., Guo, L., He, X., et al. (2018) A Graph-Theoretic Fusion Framework for Unsupervised Entity Resolution. 2018 IEEE 34th International Conference on Data Engineering (ICDE), Paris, 16-19 April 2018, 713-724. https://doi.org/10.1109/ICDE.2018.00070

为你推荐

友情链接