超声速导弹弹头热应力的有限元分析

Finite Element Analysis of Thermal Stress of Supersonic Missile Warhead

摘要: 超声速导弹飞行时面临严重的气动加热，弹头的热应力分析对其安全性至关重要。本文设计了导弹弹头的几何结构，采用四面体单元对其进行离散；考虑了SiC陶瓷材料性能随温度变化的影响，以4.3 Ma飞行环境的气动热为边界条件，建立了其热应力数学模型，进行了温度场与应力场的计算分析。结果表明，超声速弹头的气动热对结构的应力影响较大，驻点温度快速升高导致局部应力集中。本文研究结果可为超声速弹头的结构设计提供理论和数据参考。

Abstract: The supersonic missile is faced with severe aerodynamic heating in flight, and the thermal stress analysis of the warhead is very important for its safety. In this paper, the geometric structure of missile warhead is designed, the tetrahedral element is used to discretize, and the material prop-erties of SiC ceramic varying with temperature is considered. The aerodynamic heat of environment when flighting at the speed of 4.3 Ma is used as the boundary condition. The thermal stress mathematical model is established, and the temperature field and stress field are calculated and analyzed. The results show that the aerodynamic heat of supersonic warhead has great influence on the stress and deformation of the structure. And the rapid rise of stagnation point temperature leads to the local stress concentration. This study can provide theoretical and data reference for the structural design of supersonic warhead.

1. 引言

超声速导弹技术在现代化战争中具有非常重要的作用。导弹以超声速飞行时要承受极大的热载荷，服役环境严酷复杂，这对导弹的热防护提出了更高的要求。超声速导弹在设计过程中应充分考虑热应力对结构的影响，防止热应力过大引起内部的变形和功能失效，在设计之初应对导弹头部热应力进行必要的预分析。

国内外学者对弹头热环境进行了预测，导弹头部的气动热环境尤为严酷 [1] [2]。我国张超、刘洪泉 [3] 等利用有限元分析软件，对钝球头锥模型进行了飞行状态下的热环境计算。Joseph W. Cleary选用不同钝度的球锥形弹头做模型，研究了弹头表面的热流分布规律 [4]。王志超、李凰立等 [5] [6] 通过有限元分析得到了超声速弹头的气动热及温度场分布。超声速球锥形弹头的热应力分析有待作进一步深入的研究。

本文通过Nastran有限元分析软件，设计了一种球锥钝头体结构外形的SiC陶瓷导弹弹头，选取了其以4.3 Ma飞行时产生的气动热为边界条件，建立了其热应力数学模型，通过对飞行时间0~400 s内弹头的温度场和应力场进行计算分析，得到了导弹弹头温度分布规律和驻点最大温度，模拟了温度场下的应力应变云图，为实际工程结构设计提供理论与数据参考。

2. 几何外形与材料

本文参照常用导弹类型，设计了钝球头锥弹头模型，如图1所示；前端为外径500 mm的局部球形，后部为后缘外径700 mm的截锥形，通体等厚度30 mm，模型总长650 mm。

Figure 1. Outline drawing of blunt sphere cone warhead

图1. 钝球头锥弹头外形图 [7]

由于弹头要承受高温荷载，参照超声速导弹热防护文献和模型实体，结构采用SiC陶瓷材料，假设材料为各向同性，考虑材料热物性参数随温度变化的特点，具体参数如表1所示。

Table 1. Physical properties of SiC ceramics

表1. SiC陶瓷材料物理属性

3. 数学模型

对计算模型进行简化处理，弹头后部简化为几何直圆柱，故不考虑尾部效应，不考虑内部支撑和设备影响。

换热过程不计算辐射作用，只考虑气动加热对壁面的影响，结构网络的外边界看作绝热壁面，即只考虑前方空气压缩和弹头周围空气的摩擦而产生的动能转换。

简化使得计算所得热边界条件比实际情况偏高，但其误差在打样设计阶段是可以接受的 [8]。此方法保证了气动热的计算结果可以直接作为结构网络的热荷载施加于其外表面节点，大大减少了总体分析的难度和工作量 [8]。

3.1. 热流边界条件

计算超声速导弹以4.3 Ma飞行时产生的气动热，自由来流条件选取20 km处大气条件，计算条件 [9] [10] 为：温度216.7 K，密度为0.08891 kg/m³。

依据热流经验公式得到驻点热流

$q_s=\frac{1105\times {10}^5}{\sqrt{R_N}}{\left(\frac{{\rho }_{\infty }}{1.206}\right)}^{0.5}{\left(\frac{v_{\infty }}{7900}\right)}^{3.15}$ (1)

式中R为曲率半径， $\rho$ 是密度，v是飞行速度。

按照计算得到的驻点热流值，以线性过渡的方法沿导弹弹头壁面施加变化的热流。

3.2. 温度场计算

假设所用SiC陶瓷为各向同性材料，不同方向上的导热系数相同，采用傅里叶方程

$\rho c\frac{\partial T}{\partial t}=\lambda \frac{{\partial }^{2}T}{\partial x^2}+\lambda \frac{{\partial }^{2}T}{\partial y^2}+\lambda \frac{{\partial }^{2}T}{\partial z^2}$ (2)

初始条件为

${T|}_{t=0}=T_0\left(x,y,z\right)$

已知物理边界上的热流密度，边界条件为

${\left({\lambda }_x\frac{\partial T}{\partial x}{n}_x+{\lambda }_y\frac{\partial T}{\partial y}{n}_y+{\lambda }_z\frac{\partial T}{\partial z}{n}_z\right)|}_s=q_x\left(x,y,z,t\right)$

式中， $\rho$ 是密度； ${\lambda }_x,{\lambda }_y,{\lambda }_z$ 为导热系数，c为比热容，T为温度，t为时间，q为热流密度。

建立瞬态导热有限元方程，有限元格式采用部分离散的方法，在空间域内进行有限元离散后，得到一阶常微分方程组，采用时间离散+直接积分的方法进行求解 [11]。空间域离散为节点温度的常微分方程初值问题。

${\left[C\right]}^e{\left\{\stackrel{\dot{}}{T}\right\}}^e+{\left[K\right]}^e{\left\{T\right\}}^e={\left\{P\right\}}^e$ (3)

$C_{ij}={\displaystyle {\int }_{\Omega }^e\rho c{N}_i{N}_j\text{d}\Omega }$

$K_{ij}={\displaystyle {\int }_{\Omega }^e\left({\lambda }_x\frac{\partial N_i}{\partial x}\frac{\partial N_j}{\partial x}+{\lambda }_y\frac{\partial N_i}{\partial y}\frac{\partial N_j}{\partial y}\right)\text{d}\Omega }+{\displaystyle {\int }_{{\Gamma }_3}^{e}h{N}_i{N}_j\text{d}\Gamma }$

$P_i={\displaystyle {\int }_{{\Gamma }_2}^e{N}_i}{q}_s\text{d}\Gamma +{\displaystyle {\int }_{{\Gamma }_3}^e{N}_i}h{T}_f\text{d}\Gamma$

其中， $C_{ij}$ 为热容矩阵元素， $K_{ij}$ 为温度刚度矩阵元素， $p_i$ 为节点等效温度荷载元素。

对时间进行离散，分为若干个单元，在每一个时间单元内，采用向后拆分格式代替微分

$\frac{\partial T}{\partial t}=\frac{T_t-T_{t-\Delta t}}{\Delta t}$ (4)

代入(3)式得

$\left[\frac{C}{\Delta t}+K\right]{\left\{T\right\}}_t=\frac{\left[C\right]}{\Delta t}{\left\{T\right\}}_{t-\Delta t}+{\left\{P\right\}}_t$ (5)

3.3. 热应力计算

热应力分析与温度场分析采用相同的有限元网格，假设弹性模量和泊松比为常数。假设材料为各向同性，变形不影响温度，热膨胀只产生线应变，不产生切应变 [12]。

依据线弹性理论，应变由温度变化和应力共同引起

$\left\{\epsilon \right\}=\left\{{\epsilon }_e\right\}+\left\{{\epsilon }_0\right\}$ (6)

受热体弹性体的应变能

$\Pi =\frac{\text{1}}{\text{2}}{\displaystyle \underset{e}{\sum }{\left\{\delta \right\}}^{e\text{T}}}{\left[K\right]}^e{\left\{\delta \right\}}^e-{\displaystyle \underset{e}{\sum }{\left\{\delta \right\}}^{e\text{T}}{\left\{F_T\right\}}^e}$ (7)

单元刚度矩阵和热荷载分别为

${\left[K\right]}^e={\displaystyle {\int }_{V^e}{\left[B\right]}^{\text{T}}\left[D\right]\left[B\right]\text{d}v}$

${\left\{F_T\right\}}^e={\displaystyle {\int }_{V^e}{\left[B\right]}^{\text{T}}\left[D\right]\left\{{\epsilon }_0\right\}\text{d}v}$

由最小势能原理，得自由膨胀受到约束单元的平衡方程

${\left[K\right]}^e{\left\{\delta \right\}}^e={\left\{F_T\right\}}^e$ (8)

4. 有限元分析

4.1. 有限元分析步骤

针对超声速导弹弹头热应力问题，拟利用有限元方法对其计算分析，分析过程如图2所示。

Figure 2. Process of finite element analysis

图2. 有限元分析过程

4.2. 三维建模及网格划分

使用MSC.Patran前/后处理软件，根据结构尺寸建立有限元模型，使用XYZ空间直角坐标系，弹头的中心轴为Y轴，网格划分13610个三维四面体单元，三维模型示意图如图3所示，有限元网格如图4所示。

Figure 3. Schematic diagram: three-dimensional model

图3. 三维模型示意图

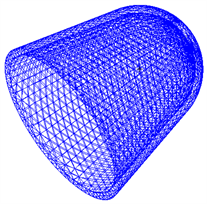
Figure 4. Schematic diagram: finite element mesh

图4. 有限元网格示意图

4.3. 边界条件的施加

将计算得到的4.3 Ma飞行导弹的气动热载荷施加到结构表面，沿弹头壁面施加变化的热流 [13]，图5可以看出弹头表面的热流分布情况，驻点处热流最大为3 × 10⁵ W/m²，后缘热流最低为1.5 × 10³ W/m²。沿模型中心轴方向(Y方向)，等距取结构面上的节点热流，得到表面热流分布曲线如图6所示。

在弹头模型后缘施加等效固定约束，使结构三个方向自由度为0，以简化导弹弹体对弹头的约束作用，方便分析弹头在气动热下的应力和位移。

Figure 5. Heat flux boundary condition

图5. 热流边界条件

Figure 6. Curve: distribution of surface heat flux

图6. 表面热流分布曲线

5. 结果分析

5.1. 温度场分析

利用Nastran求解器进行热分析计算，求得模型的温度场，获得结构网格各个节点温度随时间变化的历程。取最大时刻400 s时的温度分布如图7所示，弹头温度分布由末端沿纵向位置逐渐增大，分布规律与热流分布基本一致，驻点处受热最为严重，温度达到1060℃。因为驻点区域气流压缩强烈，动能和压缩能几乎全部转化为内能，热流密度最大，传热量最大，温度最高。图8为沿中心Y轴温度变化曲线，外表面温度变化梯度沿壁面由底部逐渐增大，这与理论分析结果吻合，温度分布规律合理。

Figure 7. Temperature field of external surface

图7. 外表面温度场示意图

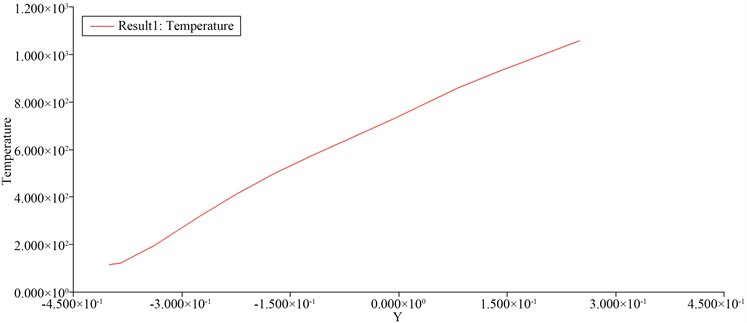
Figure 8. Curve: variation of outer surface temperature along y-axis

图8. 外表面温度沿Y轴方向变化曲线

对结构内表面温度进行分析，取最高温度时刻400 s时结构内表面的温度场云图如图9所示，弹头顶部的内表面温度最高达到870℃，驻点处内外表面温度差大约为200℃，内外表面温度分布规律一致，沿中心Y轴呈环状分布，随着加热时间的增加，热量持续不断的向导弹内部传递，导致外层的高温区不断向内扩展 [14]。

选取外表面驻点处的温度值进行分析，得到驻点处0~400 s温度值随时间变化的曲线如图10所示。分析结果可见，驻点温度表现为先增加较快，然后趋于平缓，前50 s内温度快速上升，至50 s时达到408℃；50 s后温度变化减缓，至200 s时达到720℃，400 s时达到1060℃。因为初始时刻，弹头表面与高温气体的温差相对较大，故弹头表面受热之后会立即升温，且速率较快，随着气动加热的持续进行，一方面头部结构温度升高的速率逐渐减小，另一方面头部整体温度趋于均匀，高温区的温度梯度逐渐减小，温度上升速率减缓 [14]。结果与实际飞行时弹头驻点温度变化规律基本一致。

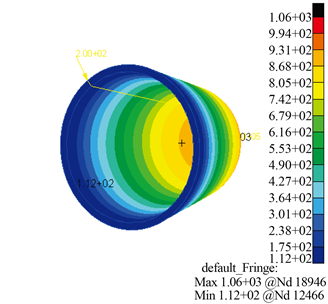
Figure 9. Temperature field of inner surface

图9. 内表面温度场示意图

Figure 10. Curve: temperature of stagnation point from 0 to 400 s

图10. 驻点温度值0~400 s变化曲线

5.2. 热应力分析

取最高温度时刻400 s时的温度场，利用Nastran进行热应力求解计算，得到结构应力和位移结果。VonMises应力如图11所示，整体应力沿中心Y轴呈环状分布，由于弹头的顶部热流较大，对热梯度更加敏感，结构强度最为薄弱，弹头尖端热应力最大达到220 MPa；应力最大值区域出现在驻点附近而非驻点处，这是由球头锥外形的曲面效应导致，与球头锥的曲率半径等有关。弹头后缘受固定约束的影响，发生应力集中现象。

位移云图如图12所示，从整体分析，弹头的热变形趋势与其温度场分布基本保持一致，弹头在高温作用下发生了明显的热膨胀，其热变形量由底部沿弹头表面随着结构温度的升高逐渐增大，其热变形量的变化梯度也在增大 [14]；结构整体的热变形与温度成正相关，符合热弹性力学的基本规律。由于SiC陶瓷的弹性模量较大，弹头顶部的变形量不大，至驻点区域处位移量为2.74 × 10⁻³ m，进一步验证了SiC陶瓷具有较好的高温力学性能。

Figure 11. Cloud chart: von Mises stress

图11. Von Mises应力云图

Figure 12. Cloud chart: overall displacement

图12. 整体位移云图

图13~15给出了弹头在X、Y、Z三个方向上应力分布情况。三个方向应力最大值相近，应力分布规律与热流分布基本一致；由图中可以看出，结构沿X方向应力分布关于YOZ平面对称，最大压应力为2200 MPa，最大拉应力为151 MPa；Y方向应力沿Y轴环状分布，且关于中心轴对称，最大压应力为2390 MPa，最大拉应力为190 MPa；Z方向应力分布关于XOY平面对称，最大压应力为2200 MPa，最大拉应力为151 MPa。从应力分布情况来看，压应力主要出现在前端表面，拉应力出现在弹头后缘。由于结构前端为弹头的高温区，且温度梯度大，造成弹头前端的各方向应力也最大，最大值的位置均在端头驻点区域。由于导弹模型采用的是各向同性的SiC材料，热膨胀系数在X、Y、Z三个方向上相同，因此，热应力在三个方向上的分布情况也基本相同。

Figure 13. Stress: X direction

图13. X方向应力

Figure 14. Stress: Y direction

图14. Y方向应力

Figure 15. Stress: Z direction

图15. Z方向应力

6. 结论

研究了一种以4.3 Ma速度飞行的SiC陶瓷钝球头锥超声速导弹弹头，建立了其数学模型，进行了气动热、温度场与应力场的计算分析；利用Nastran软件对导弹弹头结构在气动热荷载作用下的应力应变进行了有限元分析。结果表明，结构顶部的热流集中导致弹头顶端产生应力集中，热应力沿中心轴环状分布；头部前端为整个弹头的高温区，温度梯度大，造成弹头前端的热应力也最大，且最大值出现在驻点附近。因此在超声速导弹设计过程中必须考虑气动加热的影响，对弹头端部进行优化设计和热防护处理。研究成果可为实际工程设计提供分析方法和数据参考，依据弹头结构有限元计算的热应力分布，可以优化导弹弹头的结构及材料参数。

基金项目

国家自然科学基金项目资助(11772042)。

NOTES

^*通讯作者。