1. VAR模型
VAR模型提出后较广泛地应用于经济学领域。而该模型提出之前,将经济理论作为基础来刻画变量和变量存在的关系的计量经济方法是经常应用的模型,该方法存在的缺陷是,经济理论并不能充分说明变量之间的动态联系,建立起的变量之间的关系方程中,方程一侧可以有模型决定的变量出现,方程另一侧也可以有模型决定的变量出现,这使得估计和推理变得更加复杂 [1] [2]。
为了解决传统方法描述变量间关系时存在的问题,二十世纪八十年代,希姆斯将VAR模型引入到经济学中,其在经济学领域中应用的关键思路是忽略经济理论,而直接考虑与经济相关的时序变量之间的关系,多个变量置于一个模型中,即一个统一模型中包含了多个变量,多个变量的信息被共同利用,相比于单一时间序列模型,例如求和自回归移动平均(Auto Regression Integrated Moving Average, ARIMA)模型等 [3],其对隐含信息的体现更加充分,即能够完美体现真实的经济体系,所以利用该模型得到的预测值更加真实,这也促进了其在动态经济学领域中的推广使用 [4]。
某型雷达装备中关键系统的状态可以通过其关键运行参数体现出来。而且,装备系统的状态通常由多个特征参数反映,一般情况下,不是单一特征参数反映系统状态,而是多个特征参数之间相互作用共同反映系统状态,也就是说,特征参数之间存在关联关系。所以,像自回归(Auto Regression, AR)模型、自回归移动平均(Auto Regression Moving Average, ARMA)模型、ARIMA模型等针对一个指标的时间序列方法在这种情况下,不能发挥其作用。而VAR模型是处理多个相关时序指标最简便实用的模型之一 [5] [6] [7]。
2. VAR模型的基本原理
该模型核心思想是:把系统中每个变量作为系统中所有变量的相关值来建立模型,从而将单变量自回归模型推广到多元变量组成的向量自回归模型 [8]。为了详细说明构造VAR模型的过程,以两变量VAR模型为例,描述VAR模型的构造思路。模型中仅包含两个变量,变量X和变量Y,变量X由X的滞后值和Y的滞后值描述,变量Y由Y的滞后值和X的滞后值描述。假设X和Y的滞后期数都为p,那么VAR模型如下:
(1)
(2)
其中
和
为常数项,
、
、
、
(
)为参数,随机扰动项
和
的平均数值为0,方差为常数,且不存在同期相关 [8]。以上两式的矩阵描述为:
(3)
进一步可得VAR模型的一般形式:
(4)
式中的
是n维同方差平稳序列,
是参数矩阵,
是
的i阶滞后项,
是误差项,
是常数项向量。
3. VAR模型的建立
如图1所示,本文给出了VAR模型的建立过程。
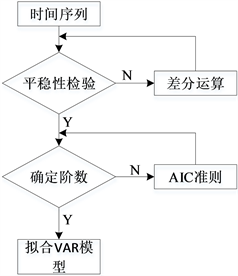
Figure 1. Steps to build a VAR model
图1. 建立VAR模型的步骤
3.1. 平稳性检验原理
如果
满足条件:
1) 均值
是与时间t无关的常数;
2) 方差
是与时间t无关的常数;
3) 协方差
是只与时间间隔k有关,与时间t无关的常数;
则称
为平稳的。
该模型要求每个变量是平稳的 [9],所以该模型建立前需要检验数据的平稳性,检验数据是否平稳的方法有多种,其中,时间序列图可以大致检验数据的平稳性,求取一组数据的平均值,观察数据序列曲线是否在均值线附近小幅变化,围绕均值线变化的数据是平稳的。另外,求解一组数据的自相关系数,当阶数越大,自相关系数越来越接近于零时,数据是平稳的。
虽然上述的两种方法可以判断序列是不是平稳的,但是对于一组非平稳数据来说,无法判断其不平稳性表现为随机性趋势,还是确定性趋势。
所谓的随机性趋势就是,不随时间改变的时间序列
,
为正时,
表现出明显的上升趋势,
为负时,
表现出明显的下降趋势,这种趋势就是随机性趋势。
所谓的确定性趋势就是,随时间改变的时间序列
,且
,
大于零时,
是明显上升的,
小于零时,
是明显下降的,这种趋势就是确定性趋势。若
,且
,则
包含上述两种趋势。
一组数据无论具有哪一种不平稳性特点,都可以采用一定的方法去除其不平稳性 [10]。
图示法和自相关分析图不能区分待检验数据包含随机性趋势还是确定性趋势,而单位根检验法可以区分时间序列存在随机性趋势还是确定性趋势。单位根检验法主要有Dickey-Fuller检验(DF检验)和ADF检验(Augmented Dickey-Fuller)。
3.1.1. DF检验原理
1) 通常情况下,如果待检验数据的平均数不等于0,并且平均数不根据时间变化,则采用模型:
(5)
该模型对应的是既包含常数项又包含随时间变化的确定性趋势的随机游走过程。若随机过程
满足
,其中
是独立的,且来自同一分布,
的平均数值为零,
的方差是有限值,则称
为随机游走过程 [11]。
该检验过程中作出的假设是,原假设
(假设
为随机游走过程);备择假设
(假设
为趋势平稳过程)。
比较显著性水平与计算所得的假设概率值,判断是否可以接受原假设。
2) 若待考察数据不包含时间趋势,则采用模型:
(6)
该模型对应的是含有常数项的随机游走过程。
检验时作出的假设是,原假设
(假设
为随机游走过程);备择假设
(假设
为平稳时间序列)。
在检验过程中,计算得出的假设概率值与确定的显著性水平进行比较,从而推断接受还是拒绝H0。
3) 如果待检验序列的均值为零时,采用模型:
(7)
该检验过程中作出的假设是,
(
为随机游走过程);
(
为平稳时间序列)。模型不包含常数项,
时序数据的平均数为0,此种情况较少,在实际应用中较少使用该情况。
3.1.2. ADF检验原理
DF检验把一组数据当做是由包含不相关关系的随机变量的一阶自回归过程
生成的,但是实际检验中,一组数据可能由高阶的自回归过程生成,所以,为满足所有数据的检验,为此提出ADF检验。
ADF检验模型包含三个:
(8)
(9)
(10)
三个模型做出的假设是,
(
不是平稳的时序数据),
(
是平稳的时序数据)。
在检验过程中,检验先从模型(8)开始,对零假设
进行检验,计算样本的t统计量,然后查询t临界值表,判断统计量与临界值的关系,如果统计量小于临界值,说明无法拒绝零假设,如果无法拒绝零假设,则继续检验模型(9),若仍无法拒绝零假设,最后检验模型(10)。当其中一个模型的检验拒绝零假设时,就可以认为序列是平稳序列,此时可以停止检验。
3.2. 差分运算原理
3.2.1. 一阶差分过程
时序数据分析过程中,差分运算是经常被使用的方法。对于时间序列
,差分运算可以表示为:
(11)
其中,
为差分算子。
3.2.2. 高阶差分过程
差分后的序列仍然可以再次进行差分,即
,这相对于原序列来说做了二次差分,方便起见差分后再差分记作
,并称之为二阶差分。二阶差分序列
与原序列
之间的关系可以表示为:
(12)
或
(13)
因此,可以认为差分运算无顺序,所以更高阶的p阶差分:
(14)
3.3. 最小信息准则(A-Information Criterion, AIC)定阶 [12]
VAR [13] 模型中的变量,有p阶滞后的阶数,因此被称为VAR(P)模型。在实际运用过程中通常希望滞后期p足够大,从而能够完整反映模型动态变化的特征,但是滞后期越长,模型中待估计的参数就越多,自由度越少,在估计模型中所包含的参数时,估计的有效性就会下降;如果滞后的阶数p过小,与其他变量无相关性的变量的自相关性会很大,这样会影响参数估计的一致性。因此需要寻求一种保证滞后的阶数和模型包含的参数都处于一个合理状态的模型定阶方法。
AIC准则——一种判断模型阶数的严谨方式 [14]。
(15)
式中,d是向量的维度,n是样本大小,p是滞后阶数,
是当滞后阶数为p时,残差向量协方差矩阵的估计。选择p的原则是在不断增加p值时,使上式值达到最小的p值。
4. 实例应用
雷达中的发射机是雷达装备系统中的重要组成部分之一,雷达射频信号正是由该装置提供的,为了保障该设备的备件充足,需要利用时间序列特征参数对设备状态进行短期预测 [15] [16] [17],解决备件的需求预测问题。为了实现发射机备件需求的预测,预测发射机特征参数具有极其重要的意义,若预测出未来某个时刻某型雷达发射机输出高压超过故障阈值,决策者可以根据预测结果决策备件需求计划的制定。
以等时距测量获得的某型雷达发射机的输出高压以及工作温度信息为原始数据,预测未来某段时间发射机输出高压和工作温度是否达到故障数据上限阈值,据此为备件需求决策提供依据。采样所得部分数据如表1所示,选择后4期为验证数据,其余的用于建立预测模型。

Table 1. Transmitter characteristic parameter sampling data
表1. 发射机特征参数采样数据
将基础数据进行归一化处理,对输出压和工作温度两个变量单独进行ADF检验。其中,经一次检验后的输出压和工作温度的pValue值如表2所示。

Table 2. One-time inspection ADF inspection value
表2. 一次检验ADF检验值
显著性水平选定0.05,输出压变量pValue值0.06大于显著性水平0.05,所以可以认为输出压序列数据时非平稳的;而工作温度变量pValue值0.02小于显著性水平0.05,可以认为工作温度序列数据是平稳的。
对输出压序列数据进行一阶差分运算,差分运算后的检验结果pValue为0.001,该值小于显著性水平,所以,经差分运算后的序列数据通过了平稳性检验。
验证序列平稳性后,需要确定时序参数VAR预测模型的阶数,让阶数从1逐渐增加,根据AIC定阶准则,当AIC尽量小时,确定最大滞后期。使用最小二乘(Ordinary Least Squares, OLS)法,求解每个方程的系数,并且通过逐渐增加阶数,从而实现为模型定阶。发射机时序参数VAR预测模型的阶数和对应的AIC如表3所示。

Table 3. Forecast model order and AIC
表3. 预测模型阶数及AIC
由表3可知,当p = 1时,AIC取得最小值−23.80727,因此确定VAR模型的阶数为1,得出输出高压的线性模型后,基于该模型对未来4期数据进行预测,并与真实测量数据进行对比分析。时序参数的预测误差率如表4所示。

Table 4. Parameter prediction error rate based on VAR model
表4. 基于VAR模型的参数预测误差率
预测数据与真实数据的逼近情况如图2所示。
VAR模型使得一个参数的预测值包含了其他影响因素的滞后值对它的影响,图2显示了该模型对发射机输出高压和工作温度的良好预测效果。
5. 结论
结合经济学领域中广泛采用的多指标时间序列模型VAR模型,论文提出将VAR模型用于预测装备特征参数,结果显示同样具有良好的预测性能。将预测结果故障上限阈值比较,辅助决策者制定备件需求计划。