1. 引言
本文考虑一个具有如下形式的可分离凸优化问题
(1.1)
其中
是有界闭合的、凸的、非空集合,
和
是凸函数(不一定是平滑函数)。
是给定的矩阵,
是一个向量。
Glowinski [1] 和Gabay [2] 证明了基于增广拉格朗日方法(ALM)的交替方向乘子方法对于问题(1.1)是非常有效的。针对问题(1.1),ALM算法的迭代形式为
(1.2)
Gabay [3] 表明ADMM算法在本质上是Douglas-Rachford分裂方法的一种应用 [4]。Cai,Gu和He在文献 [5] 中提供了一种新颖简单的邻近点算法(PPA)来解释ADMM算法,并提出了一种广义的ADMM算法(gADMM),即它首先产生了一个预测算子,形式如下:
(1.3)
其中新的迭代步表示为
。自定义矩阵表示为:
通过以上分析,可以发现针对问题(1.1),ADMM算法有许多变体。进一步研究得到,文献 [6] 中提出了DRSM算法并在 [7] 中被进一步解释为邻近点算法的应用。Jiang, B. Q.,Peng, Z.,Deng, K. K.提出了两种新颖的定制邻近点算法,在 [8] 中将建立所提出方法的全局收敛性和O (1/k)收敛速率。因此,在 [6] 中建议对PPA应用 [9] 中提出的加速方案来加速原始ADMM。最近, [10] 中的工作表明了开发下降型方法求解的可能性,其下降方向是从ADM生成的迭代中得出的。在 [11] 中,李、袁等人考虑将广义交替方向乘子法与对数-二次近端正则化相结合,以解决具有可分离结构的变分不等式问题(VI),并建立由在遍历和非遍历意义上的迭代复杂度。袁晓明提出了一种改进的基于PADM的下降方法,该方法继承了 [12] 中ADM,PPA和下降类型方法的所有优点。在 [13] 中,徐使用服从高斯分布的随机数来随机扩展步长,并针对一类变分不等式提出了随机步长收缩方法。但是,在某些实际应用中,宽松的步骤可能是不可接受的,甚至是不被允许的。
为了应对这些实际情况,本文修改了预测步长,并采用随机变量来更新步长,而不是放松固定步长。然后,提出了广义的邻近交替方乘子向法。在一些适当的假设下,本文证明了算法的收敛性。同时,本文通过数值实验,还验证了与以前提出的某些算法相比,新算法在实践中具有更好的数值性能。
本文的其余部分安排如下。本文的第2节描述了一些相关的基础知识和引理,以便后续证明。在第3节中,本文针对问题(1.1)提出了广义近邻交替方向乘子方法。所提方法的收敛性将在第4节中得到证明。在第5节中,与以前提出的算法相比,一些初步的数值结果被提出来表明新方法的高效率。第六部分总结了本文的一些结论。
2. 预备知识
本节给出了将在后续当中使用的一些预备知识。贯穿全文,本文将
表示为Educlidean范数,而
表示为内积。令
是R上的一个非空闭合子集。当
的可行集Ω是非负正数
时,向量
的每个分量i的投影很简单,表示为
。
引理2.1 令
为常数,C为非空封闭的凸集。当且仅当
是
的最优解。
记
为投影方程的残差,则
等价于找到
的零点。因此,我们可以将
记为算法的停止准则。下一个引理表明,对于任何
,
是一个非递减函数。
众所周知,对于任何x和y,正交投影算子
具有以下特性:
引理2.2 [14] 令
是一个非空闭合凸集,那么对于任意的
,都有
(1)
(2)
(3)
(4)
在许多情况下,可行集C具有以下形式:
,其中
,而Q是
的简单凸子集。基本的
可以转换为结构化的变分不等式问题,表示为
:寻找一个
,使得
其中
,
,
。
关于目标函数f的以下定义是非常重要的,并且会在后面证明会使用到。
定义2.3 设f为从
的映射。如果
,那么f在C上是单调的。
如果C是
的紧凸集,而
是连续映射,则变分不等式问题(VIP)至少具有一个解。假设函数是单调的,那么可以保证变分不等式问题的解存在且唯一。
引理2.4 如果C是
的非空闭凸集,而
是一个连续映射,那么对于任给的
,有
。
定义2.5 假设序列
是由
组成的随机变量,如果对于任意的
,有
,那么就说序列
以概率收敛到X,并且记为
。
引理2.6 马尔可夫不等式:对于任何
和
,都有
引理2.7 假设
,那么一定有
(几乎必然地)。
3. 算法提出
本节提出了一个gPADMM算法来解决问题(1.1),其中问题(1.1)的增广拉格朗日形式为
(3.1)
如果
是问题的最优解,那么存在一个
,使得
是一个鞍点,满足
(3.2)
因此,由(3.2)得出
(3.3)
根据 [12] 中的引理2.1,本文可以得到问题(3.3)的一阶最优条件:
(3.4)
因此,问题的解集也可以表示为包括所有满足条件的
,其中
,
和
(3.5)
综上所述,针对可分离凸优化问题(1.1),本文提出如下的gPADMM算法:
注3.1为了确保收敛,
需要满足是某个独立且均匀分布的扩展序列,并且
的数学期望为
。另外,在整个迭代过程不需要计算
或
。
4. 收敛性证明
在本节中,本文充分结合变分不等式来证明算法3.1的全局收敛性。因此,公式(3.6)可变为具有如下形式的变分不等式:
(4.1)
接下来将引入一些重要的引理和定理来证明算法的收敛性,如下所示。
引理4.1 令
是由公式(3.6)生成得到,那么对于任意的
是问题(1.1)的最优解,得到
(4.2)
其中
。
证明 由于
并且
,那么可知
(4.3)
将(3.6)分别加入(4.3)中且算子
和
的单调性,得出
(4.4)
因此,由(4.4) (3.6)以及
得知
(4.5)
在(4.5)的两边同时加上
及矩阵Q的定义和
,于是得到
(4.6)
这意味着
因此,引理4.1得证。
引理4.2 令
是由公式(3.6)生成得到,那么对于任意的
是问题(1.1)的最优解,有
(4.7)
证明 由引理4.1和(3.6)式得
因此,引理4.2证毕且公式(4.7)表明
是
的下降方向。
定理4.1 假设
是问题(1.1)的解,那么对任给的迭代点
,本文定义如下的一些函数:
(4.8)
那么对任意的
,存在
(4.9)
证明 由(4.8)可知
因此,(4.9)得证。
从定理4.1可知
是
的一个下界且
。由
的定义可知,它是关于
的一个二次函数,且它的最大值
。
也是最优的步长。
定理4.2 如果
,序列
是由广义的邻近交替方向乘子法生成,那么有
(4.10)
证明 由引理4.1和(3.7),我们得到
(4.11)
由于
是独立且均匀分布,可以推出
和
也是独立的。又因为
那么
的数学期望满足
最后,获得本文期望的结果。
推论4.1 如果
,序列
是由广义的邻近交替方向乘子法生成,那么有
(1) 序列
和
都是有界的。
(2) 序列
是单调且有界的。
(3)
。
定理4.3 如果
,序列
是由广义的邻近交替方向乘子法生成,那么序列
依概率收敛到
。
证明 从推论4.1和引理4.2,得到
(4.12)
因为序列
是有界的,那么它至少有一个聚集点。令
是序列
的一个聚集点,并且存在一个子序列
收敛到
,那么存在一个子序列
依概率收敛到
,记为
。
从引理2.3得到子序列
几乎必然地收敛到
,那么它也可标记子序列为
,记作
(4.13)
结合公式(3.6)、(4.12)和(4.13),有
从而有
。
因此,可以推出
。
又因为
,则
。同时因为
,且对任给地
,有
,于是得到
和
(4.14)
因此,对任意的
,由(4.14),可知
(4.15)
由此推出
。
结合引理2.2和公式(4.15),可得对任给的
,如果存在
,只要
,就有
那么得到
。
因此,序列
依概率收敛到
,记作
。
至此,收敛性证明全部完成。
5. 数值实验
本节通过数值实验重点介绍算法的有效性。
例5.1 首先,考虑陶、袁和何 [15] 提出的财务和统计问题,其形式如下:
(5.1)
其中
。
通过引入一个辅助变量Y使得
,问题(5.1)可以重新表示为如下形式的可分离凸优化问题
(5.2)
显然地,问题(5.2)是问题(1.1)的一个特殊形式,其中
。令
是线性约束
的拉格朗日乘子。对于给定的
,算法能产生第k+1次迭代步,有
(5.3)
迭代(5.3)的X-子问题是通过SVD分解来进行求解,它承担每次迭代过程中的主要计算负荷。迭代(5.3)的Y-子问题也是一个投影,有如下形式
其中
表示根据欧几里得范数到集合SB的投影。
在数值实验中,对于任意的所有
,设
是一个满足
随机矩阵。对于每个给定,将测试20个随机实例。公平地说,将X0和Y0设置为
独立性矩阵,
是一个n维零向量,并且将
记为算法的终止准则。
得到的实验结果如下图1所示。
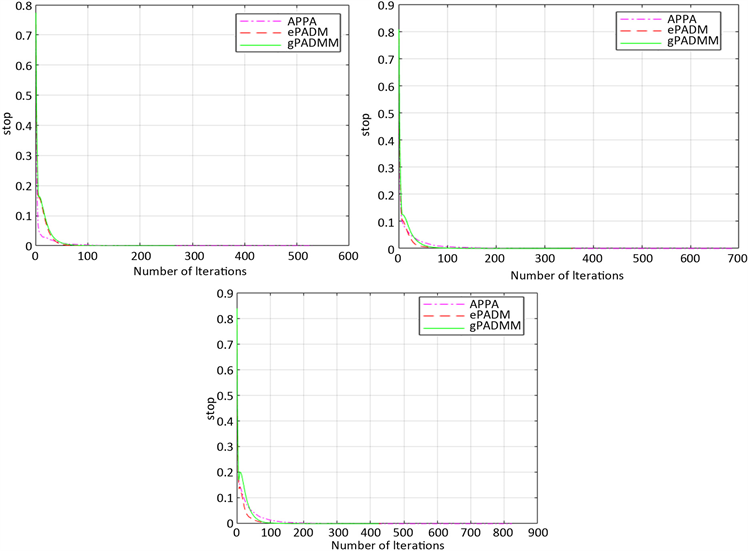
Figure 1. Comparisons of APPA, ePADM, gPADMM: n = 100, 200, 500
图1. APPA,ePADM,gPADMM三种算法的比较:n取100,200,500

Table 1. Numerical results of Example 5.1: Comparisons of APPA, ePADM, gPADMM
表1. 例5.1的实验结果:APPA,ePADM,gPADMM三种算法的比较
显然,从表1中可以看出,算法3.1的性能优于APPA算法和ePADM算法,因为其迭代和计算时间更少。因此,结果表明对于问题(1.1),提出的算法是有效的。
6. 结论
本文针对线性凸优化问题和可分离凸优化问题,提出了广义的近似交替方向乘子算法,并且通过初步实验结果验证了算法是可行的。算法3.1是一种简单且有希望的迭代方案,其收敛速度比原有算法的收敛速度快。它在其他加速技术和其他应用中进行分析和设计的潜力以及更全面的计算研究是我们进一步研究的方向。
基金项目
国家自然科学基金(72071130)。