旋转势阱耦合下孤子的研究

Study on Solitons Coupled by Rotating Potential Well

摘要: 本文研究的对象为二分量薛定谔方程，在三次非线性自吸引作用下，我们引进了一种特殊耦合作用——螺旋势阱，二分量间呈螺旋形式进行耦合。通过计算，我们得到了系统三种稳定模式的孤子，分别为L孤子、M孤子和R孤子。我们发现，通过调节旋转速度可以切换孤子的模式。同时，我们还探讨了旋转速度及分量耦合强度对孤子波函数及孤子分布的影响。

Abstract: In this paper, we study the two-component Schrödinger equation. Under the cubic nonlinear self attraction, we introduce a special coupling action spiral potential well. The two components are coupled in spiral form. Through calculation, we get three stable mode solitons of the system, which are L soliton, M soliton and R soliton. We find that the mode of soliton can be switched by adjusting the rotation speed. At the same time, we also discuss the influence of rotational velocity and component coupling strength on the soliton wave function and soliton distribution.

1. 引言

孤子是一种特殊的波包，它在传输过程中能保持其波形、能量、速度等特性不变，具有良好的稳定性，在众多领域上有着重要地位和较高的研究价值 [1] [2]。在众多孤子中，物质波孤子作为量子领域的重要学科，由于能够满足信息传递、处理所要求的准确性、稳定性与抗干扰性，其在量子信息技术上拥有广阔的研究前景。带旋转的系统会出现一些很有趣的结果，这是非旋转系统所不具有的，在旋转系统中传播的非线性光波具有许多特别的非线性动力学性质 [3] - [8]。特别是双势阱系统，在旋转作用下会出现双重对称性自发破缺现象 [9] [10] [11] [12]。二分量耦合系统较于单分量系统有着更丰富的物理现象，其孤子模式更多，是孤子研究的热门领域，带旋转的二分量系统因此备受关注。具有旋转双势阱势特性的势能项，引进了二分量同轴圆柱波导阵列，得到了很多有意义的结果，发现了多种非线性波形模式和对称性自发破缺现象 [11]；不久前，通过旋转双势阱势进行耦合作用的二分量系统也得到了研究，不同对称性性质的四种类型的非线性模式被发现，而且系统存在着双重对称性自发破缺现象 [12]。然而，这类势阱在实验上的构造存在困难，系统非线性模式的操控也存在一定的难度。在本次工作中，我们提出了一种新的二分量系统模型，该系统具有丰富的孤子模式，在实验上更容易实现，而且孤子模式操控容易，具有更高应用价值。

2. 模型及理论

我们研究的模型由一组圆柱形薄波导壳组成，波导壳间通过一个阱形的通道(红橙色区域)进行耦合，耦合通道以螺距 $2\pi /\omega$ 沿z轴方向进行螺旋，如图1所示。

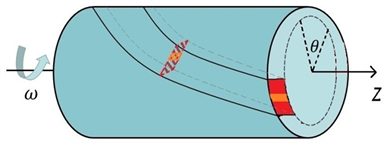
Figure 1. Coupling cylindrical thin waveguide shell

图1. 耦合圆柱形薄波导壳

沿z方向螺旋的单阱形状通道，产生了旋转势阱的效果。在波导壳足够薄的情况下，螺旋圆柱形波导壳中物质波传输的动力学行为，可以由以下二分量薛定谔方程进行描述，

$\begin{array}{l}i\frac{\partial }{\partial z}\psi =-\frac{1}{2}\frac{{\partial }^2}{\partial {\theta }^2}\psi +\gamma {\left|\psi \right|}^2\psi +C_{o}f\left(\theta -\omega z\right)\varphi \\ i\frac{\partial }{\partial z}\varphi =-\frac{1}{2}\frac{{\partial }^2}{\partial {\theta }^2}\varphi +\gamma {\left|\varphi \right|}^2\varphi +C_{o}f\left(\theta -\omega z\right)\psi \end{array}$ (1)

式(1)中， $\psi$ 和 $\varphi$ 为各波导壳中传输的波的振幅。 $\gamma$ 为三次非线性项系数， $\gamma$ 取+1，−1，分别表示自排斥和自吸引作用。本文将在三次非线性自吸引作用下探讨波动行为，即 $\gamma =-1$。其中， $\omega$ 为势阱通道的旋转速度，其取值范围为 $\left[0,0.5\right]$，即第一布里渊区(FRBZ) [8] [9] [10]。而旋转势阱作用效果由方程中的线性耦合作用项 $C_{o}f\left(\theta -\omega z\right)$ 表示，其中 $C_o$ 为耦合强度系数。

我们将在旋转参照系下探讨波的传输行为，针对耦合作用项 $C_{o}f\left(\theta -\omega z\right)$，利用变量替换 $\theta -\omega z\to \theta$，进行参照系变换，在旋转参照系下模型的动力学方程(1)变为

$\begin{array}{l}i\frac{\partial }{\partial z}\psi =-\frac{1}{2}\frac{{\partial }^2}{\partial {\theta }^2}\psi +i\omega \frac{\partial }{\partial \theta }\psi -{\left|\psi \right|}^2\psi -C_{o}f\left(\theta \right)\varphi \\ i\frac{\partial }{\partial z}\varphi =-\frac{1}{2}\frac{{\partial }^2}{\partial {\theta }^2}\varphi +i\omega \frac{\partial }{\partial \theta }\varphi -{\left|\varphi \right|}^2\varphi -C_{o}f\left(\theta \right)\psi \end{array}$ (2)

为了计算方便，我们采用矩阵形式描述方程组(2)

$i\frac{\partial }{\partial z}\chi \left(\theta ,z\right)=\hat{L}\chi \left(\theta ,z\right)-{\left|\chi \left(\theta ,z\right)\right|}^2\chi \left(\theta ,z\right)$ (3)

其中

$\chi \left(\theta ,z\right)=\left[\begin{array}{l}\psi \left(\theta ,z\right)\\ \varphi \left(\theta ,z\right)\end{array}\right]$， $\hat{L}=\left(\begin{array}{cc}\hat{h}& -\hat{C}\\ -\hat{C}& \hat{h}\end{array}\right)$，

$\hat{h}=-\frac{1}{2}\frac{{\partial }^2}{\partial {\theta }^2}+i\omega \frac{\partial }{\partial \theta }$， $\hat{C}=C_{o}f(\; \theta \; )$

$\hat{L}$ 为不含z变量的线性矩阵算符。

薛定谔方程组(3)的定态波函数表达式为

$\chi \left(\theta ,z\right)=\left[\begin{array}{l}\psi \left(\theta ,z\right)\\ \varphi \left(\theta ,z\right)\end{array}\right]=\left[\begin{array}{l}{\psi }_s\left(\theta \right)\\ {\varphi }_s\left(\theta \right)\end{array}\right]{\text{e}}^{iKz}$

其中实数K为波传播常数。

我们令 ${\chi }_s\left(\theta \right)=\left[\begin{array}{l}{\psi }_s\left(\theta \right)\\ {\varphi }_s\left(\theta \right)\end{array}\right]$，即

$\chi \left(\theta ,z\right)=\left[\begin{array}{l}{\psi }_s\left(\theta \right)\\ {\varphi }_s\left(\theta \right)\end{array}\right]{\text{e}}^{iKz}={\chi }_s\left(\theta \right){\text{e}}^{iKz}$ (4)

将等式(4)代入方程(3)中，我们得到了函数 ${\chi }_s\left(\theta \right)$ 应满足的定态方程组

$\hat{L}{\chi }_s\left(\theta \right)-{\left|{\chi }_s\left(\theta \right)\right|}^2{\chi }_s\left(\theta \right)+K{\chi }_s\left(\theta \right)=0$

定态波函数的稳定性(抗干扰性)可以利用扰动理论求解，其的无穷小扰动表达式采用以下形式

$\chi \left(\theta ,z\right)={\text{e}}^{iKz}\left[{\chi }_s\left(\theta \right)+\alpha \left(\theta \right){\text{e}}^{i\lambda z}+{\beta }^{\ast }\left(\theta \right){\text{e}}^{-i{\lambda }^{\ast }z}\right]$ (5)

其中 $\alpha \left(\theta \right)$， $\beta \left(\theta \right)$， $\lambda$ 均为任意无穷小复变量。

将式(5)代入矩阵方程(3)中，我们将得到扰动矩阵特征方程

$\left(\begin{array}{cc}-\hat{L}+2{\left|{\chi }_s\right|}^2-K& {\chi }_{{}_s}^2\\ -{\left({\chi }_{{}_s}^{\ast }\right)}^2& {\hat{L}}^{\ast }-2{\left|{\chi }_s\right|}^2+K\end{array}\right)\left(\begin{array}{l}\alpha \\ \beta \end{array}\right)=\lambda (\; \alpha \; \beta \; )$

这是以定态波函数 ${\chi }_s\left(\theta \right)$ 为变量的矩阵方程，其中 $\lambda$ 为扰动矩阵特征值， $\left(\begin{array}{l}\alpha \\ \beta \end{array}\right)$ 为相应的特征向量。如果某一波函数相关的扰动矩阵的所有特征值 $\lambda$ 均为实数，那么这个定态波函数就是稳定的。

接下来，我们引进以下几个定义，

(a) 分量中波函数的能量 $P_{\psi }$ 和 $P_{\varphi }$，定义为

$\left\{P_{\psi },P_{\varphi }\right\}={\displaystyle {\int }_{-\pi }^{\pi }\left\{{\left|\psi \right|}^2,{\left|\varphi \right|}^2\right\}\text{d}\theta }$

当然，它们满足系统(光场)的总能量守恒，

$P=P_{\psi }+P_{\varphi }$

P为我们预设的系统(光场)的总能量。

(b) 集中分布在两个波导壳中的能量可能会出现差异，我们定义相对能量破缺率，

${\Theta }_P={\displaystyle {\int }_{-\pi }^{\pi }\left|{\left|\psi \right|}^2-{\left|\varphi \right|}^2\right|}\text{d}\theta /P$

如果 ${\Theta }_P$ 大于零，则意味着集中分布在两个波导壳中的能量大小存在差异，系统发生了能量上的对称性破缺。

(c) 波形的对称性可以通过以下定义判别，

${\Theta }_{\chi }={\displaystyle {\int }_0^{\pi }\left|{\left|\chi \left(\theta \right)\right|}^2-{\left|\chi \left(-\theta \right)\right|}^2\right|}\text{d}\theta /P_{\chi }$

若 ${\Theta }_{\chi }$ 等于0，则波形 ${\left|\chi \right|}^{\text{2}}$ 具有对称性。

波导壳间的耦合势阱 $f\left(\theta \right)$ 为一特殊势阱，势阱函数是一以 $2\pi$ 为周期的周期函数， $\left[-\pi ,\pi \right]$ 区间的函数表达式及其图像如下图2。

Figure 2. Potential well function

图2. 势阱函数

3. 数值结果与分析

3.1. 稳定模式解

波在传输过程(演化)中由于色散等作用会导致波形变宽、变形和扩散，破坏波形，最终失去其原有形状及信息。而孤子则是一种特殊的波，它在传输过程中始终保持其波形不变，具有良好的稳定性，在波的研究和信号传输上有很重要的意义。我们研究的二分量薛定谔方程组(式(1))，方程引入了非线性自吸引作用和螺旋单势阱耦合作用，在它们的共同作用下，有利于孤子的存在。

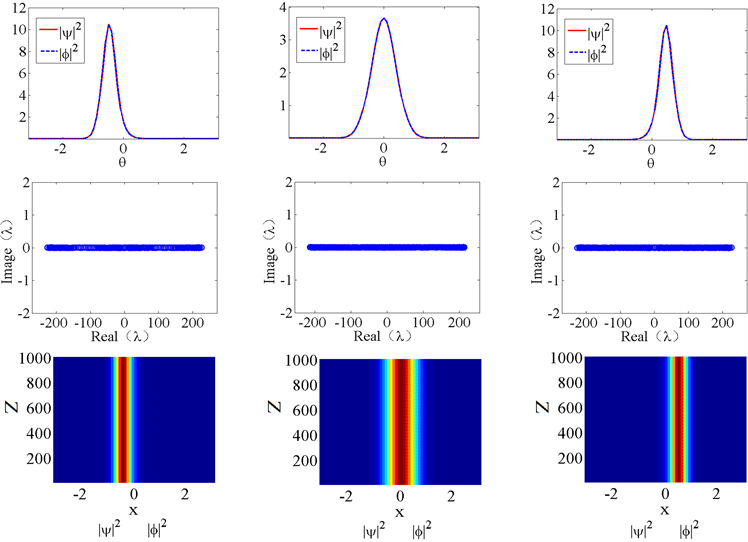
Figure 3. Three modes of soliton solution ( ${\Theta }_P=0$ )

图3. 三种模式孤子解( ${\Theta }_P=0$ )

Figure 4. Three modes of soliton solutions ( ${\Theta }_P>0$ )

图4. 三种模式孤子解( ${\Theta }_P>0$ )

虚时间演化法是求解基态波函数常用的数值方法，利用虚时间演化法，我们得到了系统三种模式的孤子解及其传输(演化)图，如图3和图4所示。图3中展示的是能量对称的孤子，波函数 $\psi$ 和 $\varphi$ 具有相同的能量，其模方波形一样，即 ${\Theta }_P=0$。而图4中的孤子发生了能量对称性破缺，集中在各波导壳中能量存在差异。图3和图4展示了三种模式的孤子解，不同孤子整体波形所处的位置各有不同，波形偏左、居中或者偏右，根据波形中心对称轴所处的位置，我们分别命名为L孤子(Left soliton)、M孤子(Middle soliton)和R孤子(Right soliton)。第二列图展示的是扰动分析的数值结果，扰动矩阵的特征值均为实数，这表示其所代表的波函数均是稳定的，具有稳定的传输性。孤子的传输图在第三列，我们可以看到在传输过程中孤子波形及能量始终保持不变，沿着单一方向稳定传输。

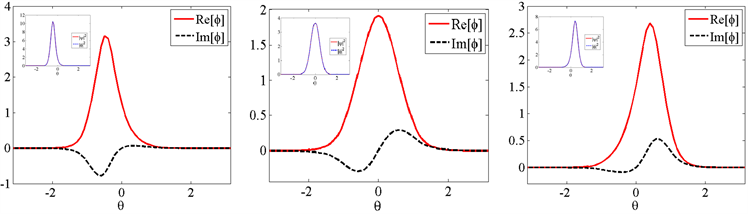
Figure 5. The real and imaginary part of the wave function graph

图5. 波函数实部与虚部图

如图5所示，从波形上来看，L孤子、M孤子和R孤子的波形基本一致，只是其集中分布区域有所不同。可是从波函数的虚部函数 $\mathrm{Im}\left[\psi ,\varphi \right]$ 的图形上看，则有很明显的区别，图5选取了波函数 $\varphi$ 的虚部和实部(波函数 $\psi$ 具有相同图像)。L孤子波函数的虚部基本为负函数( $P_{robability}\left(\mathrm{Im}\left[\psi ,\varphi \right]\le 0\right)\approx 1$ )，R孤子波函数的虚部函数则基本为正函数( $P_{robability}\left(\mathrm{Im}\left[\psi ,\varphi \right]\ge 0\right)\approx 1$ )，而M孤子波函数虚部图形则关于原点中心对称，这是不同模式孤子的一个重要特征。我们将波函数 $\varphi$ 采用以下复数形式表达，

$\varphi =\left|\varphi \right|{\text{e}}^{i\phi },\phi =\arctan \left(\frac{\mathrm{Im}\left[\varphi \right]}{\mathrm{Re}\left[\varphi \right]}\right)$ (6)

其中， $\phi$ 为波函数的辐角。从波函数辐角的角度上看，L孤子波函数 ${\varphi }_L$ 的辐角大致为负数，R孤子波函数 ${\varphi }_R$ 的辐角基本为正数，而M孤子波函数 ${\varphi }_M$ 的辐角则具有对称正负性。

3.2. 非稳定模式解

通过求解，我们发现绝大部分基态波函数解都具有很好的稳定性，但是有一类特殊的波函数解，它在传输过程中会发生偏折现象，我们称之为伪M孤子，其波形如图6所示。第一列图展示的是伪M孤子的波形图，可以看到其波形与M孤子基本一样，可是稳定性分析结果显示其扰动矩阵特征值存在着一对虚数解，这表明伪M孤子在传输(演化)过程中可能会发生变形扩散现象，其对应传输图也验证了这一结果。我们可以看到伪M孤子在传输过程中会发生传输方向偏折，方向由开始的居中方向到偏左或偏右方向，可是发生偏折后波函数在传输过程具有很好的稳定性，其波形基本保持不变与孤子具有类似行为。第二列图展示的是伪M孤子稳定性分析结果，图从左到右显示波函数存在着越来越大虚特征值，这表明波函数愈发不稳定，其发生偏折现象越早如第三列所示，这与稳定性分析结果吻合。伪M孤子的存在是可以预测的，它与模型选取的旋转势阱相关，由于势阱形状的特殊性，可以预料，相对于M孤子，L孤子和R孤子更容易存在。

Figure 6. Pseudo M soliton

图6. 伪M孤子

3.3. 旋转速度的调控作用

系统不同类型的孤子L孤子、M孤子和R孤子，可以通过调节系统(光场)的总能量P、旋转速度 $\omega$ 和耦合强度 $C_o$ 的大小得到。图3中L孤子的参数是 $\left(P,\omega ,C_o\right)=\left(12,0.25,8\right)$，M孤子的参数是 $\left(P,\omega ,C_o\right)=\left(7.4,0.25,\text{4}\right)$，R孤子的参数是 $\left(P,\omega ,C_o\right)=\left(12,0.35,8\right)$。而图4中孤子的数值参数如下，L孤子的参数是 $\left(P,\omega ,C_o\right)=\left(10,0.3,\text{5}\right)$，M孤子的参数是 $\left(P,\omega ,C_o\right)=\left(12,0.25,\text{6}\right)$，R孤子的参数是 $\left(P,\omega ,C_o\right)=\left(10,0.2,\text{5}\right)$。对比L孤子和R孤子的数值参数，我们发现在总能量P和耦合强度 $C_o$ 固定的情况下，调节旋转速度 $\omega$，可以对L孤子和R孤子进行模式切换，这是一个很有意思的发现。L孤子和R孤子类比于二进制中的0和1，而旋转速度 $\omega$ 就是二进制进位按钮，只需要调节 $\omega$ 我们就可以进行信息编码。接下来，我们将进一步讨论旋转速度 $\omega$ 对孤子模式的调控作用。

图7展示的是L孤子和R孤子在不同旋转速度下波形图和其波函数图，图a为L孤子，是在三组不同旋转速度下取得，分别为 $\left({\omega }_1,{\omega }_2,{\omega }_3\right)=\left(0.15,0.3,\text{0}\text{.4}\right)$。图b为R孤子，是在旋转速度 $\left({\omega }_1,{\omega }_2,{\omega }_3\right)=\left(0.1,0.25,\text{0}\text{.45}\right)$ 下取得，图a、b的共同参数为 $\left(P,C_o\right)=\left(10,5\right)$。波函数的虚部对孤子模式类型的表征有重要作用，通过图a和图b，我们发现旋转速度对波函数的虚部有着较大的影响，旋转速度越大，波函数虚部的绝对值 $\left|\mathrm{Im}\left[\psi ,\varphi \right]\right|$ 越大，而孤子的形状(波函数的模方)则基本保持不变，通过公式(6)从辐角上看，旋转速度与 $\left|\phi \right|$ 呈正相关关系。

3.4. 耦合作用的调控作用

对称性是物理上一个非常重要的概念，通过研究孤子解的对称性能进一步深入了解系统。在波函数传输(演化)过程中，分量间会通过耦合作用进行信息交流，相互作用，本章节将探讨耦合作用对孤子对称性的影响。数值结果如图8所示，选定参数为 $\omega =0.25$。从图(a)中我们可以知道，当耦合作用较弱时，

(a) L孤子 (b) R孤子

Figure 7. Waveforms of soliton at different rotation speeds

图7. 不同旋转速度下孤子的波形

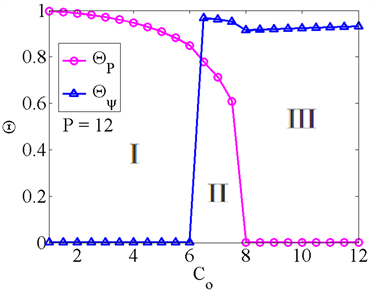
(a) (b) (c) (d)

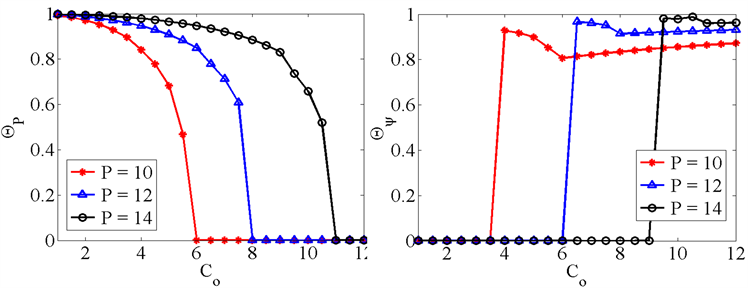
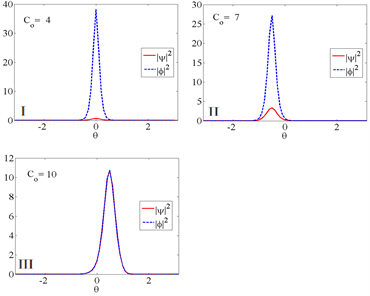
Figure 8. The effect of coupling on soliton

图8. 耦合作用对孤子的影响

孤子会发生能量对称性破缺，而且随着系统能量的增强，孤子更容易发生能量对称性破缺。图(b)展示的是 $C_0-{\Theta }_{\psi }$ 图， ${\Theta }_{\psi }$ 描述的是孤子波形上的对称性， ${\Theta }_{\psi }=0$ 表示的是M孤子，当 ${\Theta }_{\psi }>0$ 则表示L和R孤子。图(b)表明L和R孤子更容易存在强耦合、低能量下，而M孤子则更倾向于存在于弱耦合、高能量下。为了更好地了解孤子的分布情况，我们求解出了某一固定能量( $P=12$ )下的 $C_0-\Theta$ 图，如图(c)所示， $C_0-\Theta$ 平面划分出了三个区域，图(d)分别对应着三种模式的孤子，而能量对称性守恒( ${\Theta }_P=0$ )模式下M孤子并不存在，能量对称性守恒的M孤子应存在于低能系统中。

4. 结论

在三次非线性自吸引和螺旋单势阱耦合的共同作用下，通过调控系统(光场)的总能量P、旋转速度 $\omega$ 和耦合强度 $C_o$ 的大小，我们得到了系统三种稳定模式的孤子——L孤子、M孤子和R孤子，不同模式孤子解可通过其波函数的虚部进行表征。同时，我们也发现了系统一种特殊的模式解——伪M孤子，它在传输过程中会发生偏折，并且具有一定的稳定性。进一步分析，我们发现调节旋转速度 $\omega$，可以进行L孤子和R孤子模式间的切换，旋转速度 $\omega$ 起到了二进制进位按钮的作用，通过调节 $\omega$ 我们可以对信息进行编码存储。波函数虚部对孤子模式表征有重要作用，旋转速度越大，波函数虚部的绝对值 $\left|\mathrm{Im}\left[\psi ,\varphi \right]\right|$ 越大，则波函数辐角变化越大。在弱耦合、高能系统中，系统更容易引发能量对称性破缺；L和R孤子更容易存在强耦合、低能量系统下，而M孤子则更倾向存在于弱耦合、高能量系统下，但是在弱耦合、高能系统中，系统会发生能量对称性破缺，此时将不存在能量对称性守恒的M孤子。