1. 引言
随着社会的发展和科技的进步,延时系统在生物、经济和自动化控制等诸多领域日益受到重视 [1] [2]。参数辨识是设计、分析与控制实际系统的重要前提 [3]。
时域方法 [4] [5] [6] 是延时系统参数辨识领域的重要方法。基于梯度的辨识算法近年来受到许多学者的关注。文献 [7] [8] [9] 应用变分方法计算梯度并提出一种参数辨识算法;文献 [10] 求得了准则函数对参数的梯度所满足的系统,并由此给出了一种辨识算法。
本文受文献 [11] 启发,研究了一类线性多延时系统的系数和延时量的辨识问题。本文的主要工作是设计了关于系数矩阵和延时量的准则函数,利用最小二乘原理给出了固定延时量时系数矩阵的最小二乘解,从而将系数矩阵和延时量的同时估计问题看作仅关于延时量的估计问题,利用梯度方法求解优化问题得出延时量,最终用估计出的延时量求解矩阵方程求得系数矩阵。
2. 问题描述
考虑以下线性延时系统:
(1)
其中
表示状态向量;
表示控制向量;
,
是系统的参数矩阵;初始函数
;这里假定系统的延时量满足
。
记
,
。
定义2.1 设矩阵
,称
为Q的Frobenius范数。
命题2.1 设
,则
引理2.1 [12] 若A是列满秩矩阵,B是行满秩矩阵,矩阵
满足
那么在最小二乘意义下上式有唯一解
。
命题2.2 设矩阵函数
可逆且可导,则
。
命题2.3 设矩阵函数
可导,则
本文的目的是通过求解如下的优化问题辨识参数
,
(2)
其中
(3)
3. 算法的推导
固定延时量
,式(2)中
有唯一最小二乘解。从而对优化问题(2)的求解可转化为只与
有关的优化问题。接下来,利用新目标函数关于
的梯度采用动量梯度法估计延时量。最后,求系数矩阵关于式(2)的最小二乘解。
3.1. 梯度的计算
定理3.1 对于式(2)所述的优化问题,当
固定时有唯一最小二乘解
(4)
其中
(5)
(6)
证明。
由命题2.1,上式可写为
。
由引理2.1上式中
有唯一最小二乘解。
(7)
根据定理3.1可知,优化问题(2)可以转化为
(8)
接下来分三个定理求
。
定理3.2 设
,则
证明。
定理3.3 设
,则
其中
。
证明。
由命题2.2得
定理3.4 式(8)对延时量
的偏导数如下
(9)
证明。
3.2. 算法描述
本文采用动量梯度法进行联合估计(见算法1)。
4. 数值算例
本节给出两个数值算例来验证结果的有效性
例4.1 考虑不稳定的线性单延时系统(1),系统参数如下
输入函数为
,初始函数为
。
初始点
,参数
。
利用算法1出参数
用算法1估计例4.1中延时量的迭代过程如图1所示。
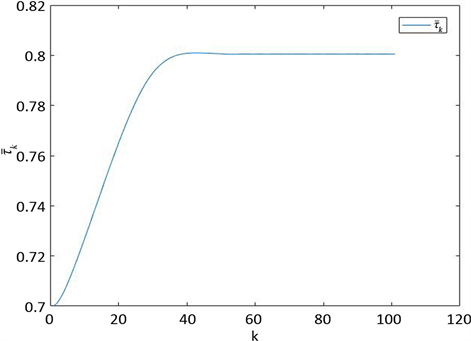
Figure 1. Iterative process of delay estimation
图1. 延时量估计的迭代过程
例4.2 考虑线性多延时系统(1),系统参数如下
输入函数为
,初始函数为
.
初始点
,参数
.
利用算法1出参数
用算法1估计例4.2中两个延时量的迭代过程通过等高线图方式呈现如图2所示。将图2中目标函数和迭代过程用三维曲面呈现后如图3所示。
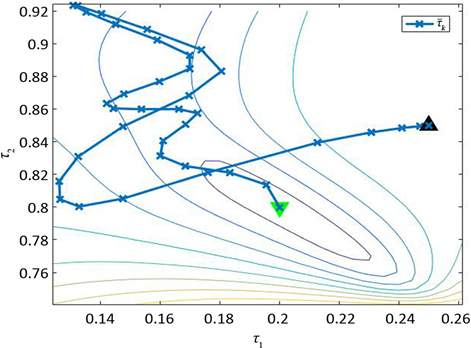
Figure 2. Iterative process of two delay estimation
图2. 两个延时量估计的迭代过程

Figure 3. The iterative process and objective function of the delay amount
图3. 延时量的迭代过程及目标函数
5. 结论
针对线性多延时系统,给出了一种含积分的目标函数。通过最小二乘方法将联合参数的目标函数转化为仅依赖延时量的非线性函数。采用动量梯度方法求解关于延时量的优化问题。确定延时量后求矩阵方程的最小二乘解估计系数矩阵。通过数值仿真验证了算法的有效性。