1. 绪论现状
1.1. 研究背景及现状
非线性偏微分方程的研究在很早之前就已经得到了广大学者的关注。特别是在数学、物理、化学等学术领域中,非线性偏微分问题得到了广泛的应用。近些年来,关于
-Laplacian问题解的存在性、唯一性和正则性结果已经得到了大量完整的结论 [1] [2] [3]。如今,
-Laplacian问题在处理一些全变分图像恢复问题、数学图像处理和计算视觉等方面有了进一步的深入研究 [4] [5] [6]。这些变量指数椭圆问题的解决,对数学学科以后的发展具有很大的影响。
本文将在学者的基础上,深入探究
-Laplacian问题在局部、非局部情况下解的存在性,可以说
-Laplacian为
-Laplacian问题的自然拓展,考虑了一种新的变化图像能够去噪的模型。
近些年来,变量指数椭圆问题吸引了广大学者的关注。2010年,Andreianov、Bendahmane等 [7] 研究了下列典型问题
(1.1)
得到了方程(1.1)弱解的存在性。进一步,为了在
中使得相关的解是保序且收缩的。2019年,Chipot、Oliverira [8] 考虑了如下方程
(1.2)
其中
是一个光滑有界区域,
是给定的函数并且
为变量指数函数,用小扰动的方法证明了弱解的存在性。方程(1.2)的提出源于Zhikov [9] 介绍的
-Laplacian方程的拓展。在过去的二十年里,人们对这一领域的兴趣主要来源于建模应用 [10] [11],例如热流体或电流变流体和图像复原 [12]。
2019年,Chipot、Oliverira [8] 研究了非局部情形下的方程
(1.3)
其中
为给定的函数,
,
为非线性指数的函数,这里
。在这种情况下,给出映射b的一些合适的例子,例如
或者对于
且
,
。通过Schauder不动点定理研究了其弱解的存在性问题。
1.2. 预备知识
这一部分介绍本文用到的数学符号和基础知识。
变指数函数p由弱解u决定,而u最终取决于变量x。p可以写成可变指数
:
。这可以促使我们在指数可变的Sobolev空间中寻找方程的解。在过去的20年。函数空间的数学理论发展得如此之快,以至于现在可以用这个理论来分析原方程。因此我们可利用具有可变指数的Lebesgue空间及Sobolev空间的性质来解决问题 [2] [10] [11]。符号“
”和“
”分别表示在相应空间中强收敛和弱收敛。
令
表示所有Lebesgue可测函数
的集合,并定义:
其中
。定义
为所有Lebesgue可测函数
的空间且满足,
其对应Luxembourg范数为
,
为巴拿赫空间。
若对任意的
满足
(1.4)
则
是可分的,且
在
中稠密。同时,
在
中也稠密。
若对任意的
满足
(1.5)
则
是自反的。在方程(1.5)成立的情况下,定义
为
的对偶空间,其中
为
的Holder共轭,且两者满足
。
从
的定义及方程(1.5)中,我们可以得到
同时,从
空间及其范数的定义可知,若方程(1.5)成立,则满足
同时,利用这两个方程,我们可以得到
(1.6)
Young不等式:对任意的
,
及正常数
,任意的 都有
都有

Holder不等式:对任意的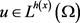 ,
, ,都有
,都有
 (1.7)
(1.7)
同时,若方程(1.7)成立,则对h满足方程(1.4)且对有界区域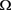 ,都有
,都有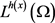 连续嵌入到
连续嵌入到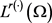 中,其中
中,其中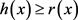 对几乎处处的
对几乎处处的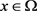 都成立。
都成立。
假设对任意的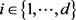 都有弱导数
都有弱导数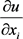 ,定义空间
,定义空间

其对应范数 。
。
若方程(1.4)成立,则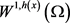 可分;若方程(1.5)成立,则
可分;若方程(1.5)成立,则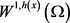 自反,同时当
自反,同时当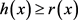 对几乎处处的
对几乎处处的 ,都有
,都有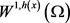 连续嵌入到
连续嵌入到 成立。定义空间
成立。定义空间 ,其对应范数为
,其对应范数为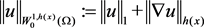 ,若
,若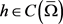 ,则
,则 的范数等价于
的范数等价于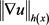 。
。
不同于经典Sobolev空间,在空间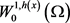 中,光滑函数不一定是稠密的。故定义
中,光滑函数不一定是稠密的。故定义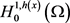 为范数
为范数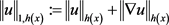 定义下
定义下 的闭包,且满足
的闭包,且满足 。
。
若 为有界区域,
为有界区域, 为Lipschitz连续,且h满足局部Holder连续,则
为Lipschitz连续,且h满足局部Holder连续,则 在
在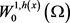 中稠密。
中稠密。
局部Holder连续:若满足
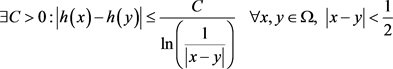 (1.8)
(1.8)
则h为局部Holder连续。也就是

其中 且定义为
且定义为 对
对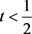 为连续递增的函数,使得
为连续递增的函数,使得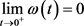 。若方程(1.8)成立,则
。若方程(1.8)成立,则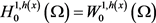 。特别的,若对
。特别的,若对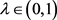 有
有 ,则h为局部Holder连续。
,则h为局部Holder连续。
局部Holder连续的性质对变量指数Sobolev空间中建立Sobolev不等式是非常重要。定义 的点态Sobolev共轭为:
的点态Sobolev共轭为:
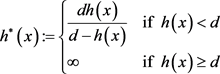
若在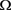 中h为可测函数满足
中h为可测函数满足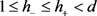 且方程(1.8),则有
且方程(1.8),则有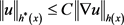 ,对任意的
,对任意的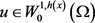 ,其中正常数C取决于
,其中正常数C取决于 ,d及方程(1.8)。另一方面,若h满足方程(1.8)且
,d及方程(1.8)。另一方面,若h满足方程(1.8)且 ,则有
,则有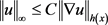 ,对任意的
,对任意的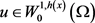 都成立,其中正常数C取决于
都成立,其中正常数C取决于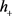 ,d及方程(1.8)。
,d及方程(1.8)。
引理1.3.1 [13] 假设对几乎处处的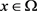 ,常数
,常数 和
和 ,以及任意的
,以及任意的 ,满足以下条件:
,满足以下条件:
i)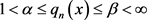 ;
;
ii) 当 时,在
时,在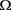 中有
中有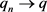 ;
;
iii) 当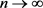 时,在
时,在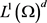 中
中 弱收敛于
弱收敛于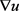 ;
;
iv) 对常数C有 ;
;
则有
 (1.9)
(1.9)
 (1.10)
(1.10)
证明:由Young不等式得:对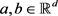 ,
,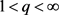 及
及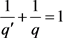 ,有
,有

得到
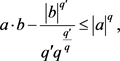 (1.11)
(1.11)
令b为 中的函数,
中的函数,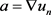 ,
,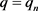 代入方程(1.11),由假设i)得到
代入方程(1.11),由假设i)得到
 (1.12)
(1.12)
由假设ii) iii),使得方程(1.12)中取极限 时
时
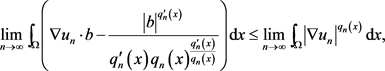
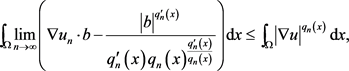
得
 (1.13)
(1.13)
令 ,这里
,这里 ,即
,即 ,
,
代入上式
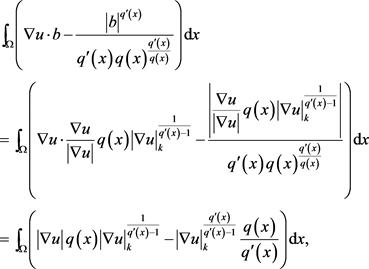
所以

当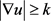 时,
时,
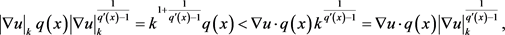
当 时,
时,

所以,得到
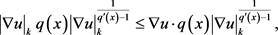
故
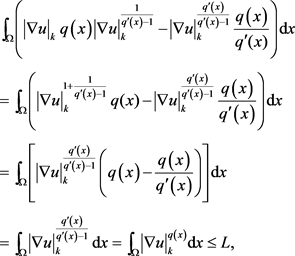
令 ,则
,则
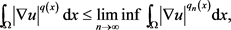
由iv),得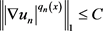 ,即
,即
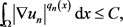
继而得到
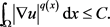
2. 局部问题解的存在性
2.1. 引言
本章研究在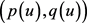 为局部情况时,如下变量指数椭圆方程:
为局部情况时,如下变量指数椭圆方程:
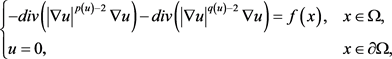 (2.1)
(2.1)
其中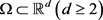 是一个光滑有界区域,
是一个光滑有界区域, 是给定的函数并且
是给定的函数并且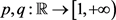 为变量指数函数。利用奇异摄动技术和Schauder不动点定理证明了局部问题(2.1)的弱解的存在性。
为变量指数函数。利用奇异摄动技术和Schauder不动点定理证明了局部问题(2.1)的弱解的存在性。
2.2. 准备知识
首先定义方程(2.1)弱解的集合如下:

若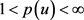 ,对所有的
,对所有的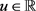 ,则这个集合为Banach空间。
,则这个集合为Banach空间。
范数 定义为:
定义为:
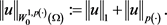
同时,若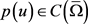 ,则范数等同于
,则范数等同于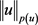 。另外,若对于常数
。另外,若对于常数 ,满足
,满足 ,p连续,则由方程(1.8)可知,
,p连续,则由方程(1.8)可知, 是
是 的闭子集,且
的闭子集,且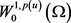 是可分的和自反的。
是可分的和自反的。
另外,对 ,定义
,定义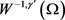 为
为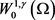 的对偶空间。
的对偶空间。
2.3. 主要结论
这一部分,简述本章的主要结论。
定义2.3.1假设方程(2.1)中的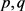 连续,且满足对任意
连续,且满足对任意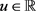 ,
,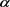 和
和 为常数,有
为常数,有

且f满足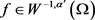 。若u满足
。若u满足

则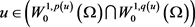 为方程(2.1)的弱解。
为方程(2.1)的弱解。
其中 为
为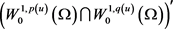 与
与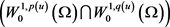 的内积。
的内积。
定理2.3.2 令 为有界区域,且边界
为有界区域,且边界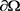 满足Lipschitz连续。同时,假设
满足Lipschitz连续。同时,假设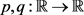 为Lipschitz连续函数,对任意
为Lipschitz连续函数,对任意 ,有
,有
 (2.2)
(2.2)
且f满足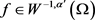 ,则方程(2.1)至少有一个弱解。
,则方程(2.1)至少有一个弱解。
2.4. 局部问题解的存在性
首先,考虑以下方程:对任意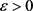 ,有
,有
 (2.3)
(2.3)
这里 为方程(2.2)的常数。接下来,我们给出方程(2.3)弱解的定义。
为方程(2.2)的常数。接下来,我们给出方程(2.3)弱解的定义。
定义2.4.1 假设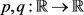 为Lipschitz连续函数,且满足方程(2.2),若u满足对任意的
为Lipschitz连续函数,且满足方程(2.2),若u满足对任意的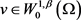 ,有
,有

则u为方程(2.3)的弱解。
其中 为
为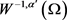 和
和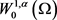 的内积。
的内积。
引理2.4.1 假设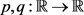 为Lipschitz连续函数,且满足方程(2.2),f满足
为Lipschitz连续函数,且满足方程(2.2),f满足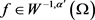 ,则方程(2.3)存在一个弱解
,则方程(2.3)存在一个弱解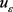 。
。
证明:给定 。由方程(2.2)及f的假设条件,可得对几乎处处的
。由方程(2.2)及f的假设条件,可得对几乎处处的 ,有
,有
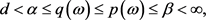 (2.4)
(2.4)
且

因此固定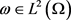 ,由算子的单调性,可知方程对任意的
,由算子的单调性,可知方程对任意的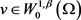
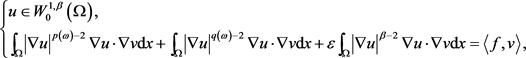 (2.5)
(2.5)
存在唯一弱解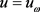 。将
。将 代入上式,利用Holder不等式,得
代入上式,利用Holder不等式,得
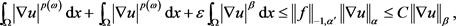
其中正常数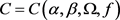 。因此,若对
。因此,若对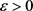 ,
,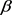 为方程(2.2)中的上常数,则得到
为方程(2.2)中的上常数,则得到
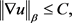 (2.6)
(2.6)
其中正常数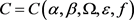 ,与w无关。
,与w无关。
并且,由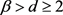 ,可知
,可知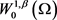 紧嵌入
紧嵌入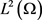 中,即得
中,即得 ,其中正常数
,其中正常数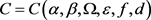 与w无关。因此,考虑映射
与w无关。因此,考虑映射 ,其中
,其中 及
及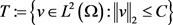 ,下面证明映射B是连续的:
,下面证明映射B是连续的:
事实上,假设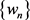 为
为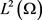 中的序列,使得
中的序列,使得
在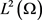 中,当
中,当 ,有
,有
 (2.7)
(2.7)
当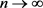 时,在
时,在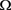 中几乎处处有
中几乎处处有
 (2.8)
(2.8)
对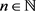 ,令
,令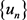 为方程组(2.5)的解,且令
为方程组(2.5)的解,且令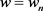 ,也就是满足对任意
,也就是满足对任意 ,
,
 (2.9)
(2.9)
结合方程(2.6),可得到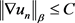 ,其中C不依赖于n。
,其中C不依赖于n。
因此,由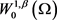 的自反性,这里我们将序列记作
的自反性,这里我们将序列记作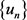 ,可知存在
,可知存在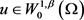 使得
使得
在 中,当
中,当 时,有
时,有
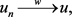 (2.10)
(2.10)
在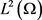 中,当
中,当 时,有
时,有
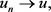 (2.11)
(2.11)
考虑到方程组(2.9)的第二行,可得对任意的
 (2.12)
(2.12)
由单调性,可得对任意的
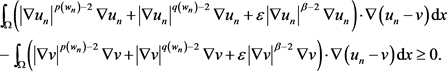 (2.13)
(2.13)
将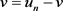 代入方程(2.12),并且利用方程(2.13),可知对
代入方程(2.12),并且利用方程(2.13),可知对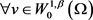 ,有
,有
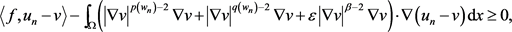 (2.14)
(2.14)
根据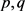 的假设及勒贝格定理可知对任意的
的假设及勒贝格定理可知对任意的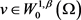
在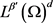 中,当
中,当 时,有
时,有
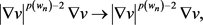 (2.15)
(2.15)
在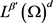 中,当
中,当 时,有
时,有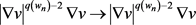 。
。
利用方程(2.10)和方程(2.15),在方程(2.14)中取极限,即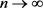 ,则对任意的
,则对任意的 ,有
,有
 (2.16)
(2.16)
令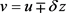 ,其中
,其中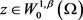 ,
,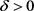 。由方程(2.16),可得
。由方程(2.16),可得
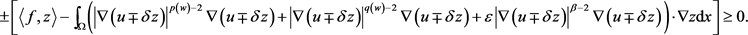
即
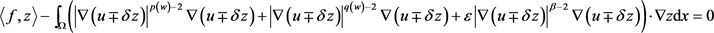
上式中,令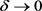 ,则容易得到任意的
,则容易得到任意的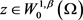 ,有
,有
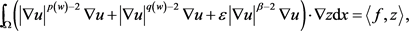
即由唯一性可知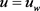 。故由方程(2.11)可知,在
。故由方程(2.11)可知,在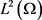 ,当
,当 时,
时,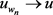 。
。
由极限的唯一性可得,在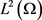 ,当
,当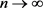 时,
时,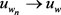 。
。
所以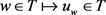 是连续的。
是连续的。
因此,有Schauder不动点定理,映射B有唯一的不动点,故引理2.4.1成立。
定理2.3.2的证明。由引理2.4.1,可得对任意的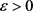 ,存在
,存在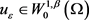 ,有任意的
,有任意的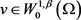 满足
满足
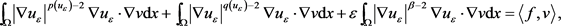 (2.17)
(2.17)
且对任意的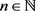 几乎处处的
几乎处处的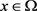 ,有
,有
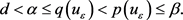
令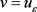 代入方程(2.17),得
代入方程(2.17),得
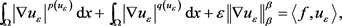 (2.18)
(2.18)
根据方程(1.6),得
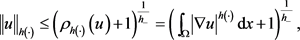
因此由Holder不等式(1.7)得
 (2.19)
(2.19)
这里 。因此有
。因此有
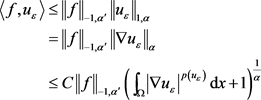 (2.20)
(2.20)
由杨不等式,可知
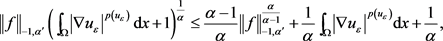
结合方程(2.18)和方程(2.20),得到
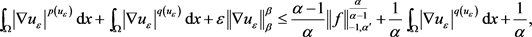
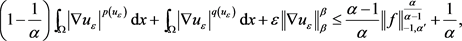
由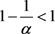 ,得
,得
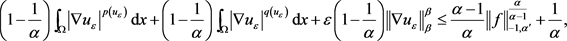
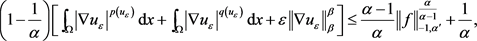
方程两边同时除以 ,得
,得
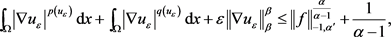
因此,由 的有界性,得
的有界性,得
 (2.21)
(2.21)
这里常数C不依赖于 。方程(2.19)有
。方程(2.19)有
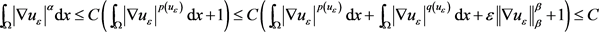
从而得到
 (2.22)
(2.22)
这里常数C不依赖于 。由于
。由于 紧嵌入
紧嵌入 ,表明对于序列
,表明对于序列 ,这里存在
,这里存在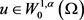 ,使得
,使得
在 中,当
中,当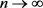 时,
时,
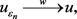 (2.23)
(2.23)
在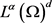 中,当
中,当 时,
时,
 (2.24)
(2.24)
在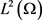 中,当
中,当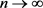 时,
时, 。
。
在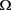 中,当
中,当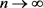 时,几乎处处有
时,几乎处处有
 (2.25)
(2.25)
根据方程(2.2)和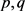 的假设,得
的假设,得 ,
,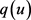 为Holder连续。利用方程(2.25),得到当
为Holder连续。利用方程(2.25),得到当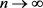 时
时
 (2.26)
(2.26)
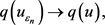 (2.27)
(2.27)
和
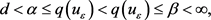 (2.28)
(2.28)
在方程(2.21)中,令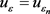 ,结合方程(2.21),(2.24),(2.26),(2.27)和(2.28),由引理1.3.1可得
,结合方程(2.21),(2.24),(2.26),(2.27)和(2.28),由引理1.3.1可得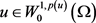 和
和
因此可得
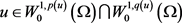 (2.29)
(2.29)
在方程(2.17)中,令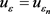 和
和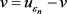 ,得到对于任意的
,得到对于任意的 ,有
,有
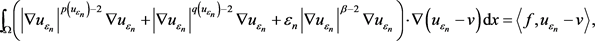 (2.30)
(2.30)
且有单调性,可得对任意的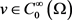 ,有
,有
 (2.31)
(2.31)
将方程(2.30)代入方程(2.31),得到对任意的
 (2.32)
(2.32)
结合方程(2.15)和方程(2.25),可得对于任意一个v,在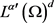 中,当
中,当 时,有
时,有
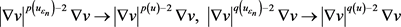 (2.33)
(2.33)
结合方程(2.22),(2.23)和方程(2.33),在方程(2.32)中取极限 ,得到对任意的
,得到对任意的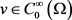 ,有
,有
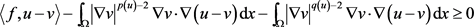 (2.34)
(2.34)
根据方程(2.2)和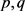 的假设,
的假设, 和
和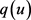 为Holder连续函数,因为稠密性,得
为Holder连续函数,因为稠密性,得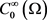 在
在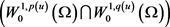 中稠密,进一步得到对
中稠密,进一步得到对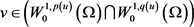
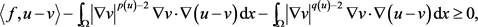 (2.35)
(2.35)
此外在方程(2.35)中令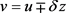 ,这里
,这里 ,
,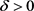 ,得
,得
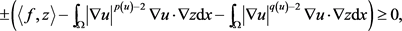
因此

结合方程(2.29)可知,定理2.3.2成立。