1. 引言
近年来,相对同调代数,特别是其中的Gorenstein同调理论受到代数学界专家们的广泛关注。1995年,Jenda和Enochs在 [1] 中,作为G-维数为0的模的推广,引入了Gorenstein投射模和Gorenstein内射模的概念;为了与平坦模对应,1993年,Enochs,Jenda和Torrecillas在 [2] 中定义了Gorenstein平坦模。Ding,Li和Mao在 [3] 中考虑了Gorenstein投射模的一种特殊情况,即强Gorenstein投射模。因为Ding,Li和Mao在这方面的杰出工作,Gillespie在 [4] [5] 中称强Gorenstein投射模为Ding投射模。
最近,Saroch和Stovicek在 [6] 中引入了一个新的模,即投射余可解的Gorenstein平坦模。Iacob在 [7] 中对这些模的类进行了细致的研究,证明了投射余可解的Gorenstein平坦模的类与Ding投射模的类等价当且仅当每一个Ding投射模是Gorenstein平坦模,最后证明了在凝聚环的条件下投射余可解的Gorenstein平坦模的类与Ding投射模的类等价。同时也给出了投射余可解的Gorenstein平坦模的类与Gorenstein投射模的类等价的一些充分必要条件。为了进一步刻画Gorenstein同调代数在一般环上的性质,Bravo,Gillespie和Hovey在 [8] 中引入了Level模的概念,这是对平坦模的自然推广,继而引入了Gorenstein AC投射模。在Noetherian环上,Gorenstein AC投射模就是Gorenstein投射模。在凝聚环上,Gorenstein AC投射模就是Ding投射模。
受上述研究的启发,本文研究了Gorenstein AC投射模的类与投射余可解的Gorenstein平坦模的类等价以及Gorenstein AC投射模的类与Gorenstein投射模的类等价的一些充分必要条件。
2. 预备知识
除非特别说明,本文中所有的环R是结合环,所有的R-模都是左R-模。投射模的类,内射模的类,平坦模的类以及Level模的类分别用
、
、
、
表示。
表示R-模范畴。对于任意R-模的类
,我们记:
,
。
定义2.1 1) 称R-模F是超有限表示模,如果R-模F有一个投射分解
其中
是有限生成的。
2) 称R-模L是Level模,如果对任意的超有限表示模F,有
。
3) 称R-模A是绝对clean模,如果对任意的超有限表示模F,有
。
定义2.2 考虑投射R-模的正合列
其中
。
1) 若对任意的投射R-模Q,有
正合,则称R-模M是Gorenstein投射模。用
表示Gorenstein投射模的类。
2) 若对任意的平坦R-模F,有
正合,则称R-模M是Ding投射模。用
表示Ding投射模的类。
3) 若对任意的Level R-模L,有
正合,则称R-模M是Gorenstein AC投射模。用
表示Gorenstein AC投射模的类。
4) 若对任意的内射右R-模I,有
正合,则称R-模M是投射余可解的Gorenstein平坦模。用
表示投射余可解的Gorenstein平坦模的类。
定义2.3 称 R-模M是Gorenstein平坦模,如果存在平坦R-模的正合列
其中
,使得对任意的内射右R-模I,有
正合。用
表示Gorenstein平坦模的类。
定义2.4 称R-模M是强Gorenstein投射模,如果存在投射R-模的正合列
其中
,使得对任意的投射R-模Q,有
正合。
注记 由定义可知,
,
。
3. 主要结果
命题3.1 设R是任意环。则下列条件等价:
1)
。
2) 对任意的R-模
,有
。
3)
。
证明 1) ⟹ 2) 设
。因为
,所以M是Gorenstein平坦的,从而由( [9],定理3.6)知,
。
2) ⟹ 1) 设
。则存在投射R-模的正合列
其中
,
且对任意的Level R-模L,有
正合。所以有内射R-模的正合列
又由假设知
,所以对任意的内射右R-模I,有
正合。由伴随同构知
,所以
正合。又因为
是忠实内射的,所以
正合,因此
。
2) ⟹ 3) 设
。则
。从而对任意的内射右R-模I,有
,
所以
。
3) ⟹ 2) 设
。则存在投射R-模的正合列
其中
且有
。因为
,所以对任意的内射右R-模I,有
。因此对任意的内射右R-模I,有
。故对任意的内射右R-模I,
正合且
是内射模的正合列。从而证得
。
下面我们讨论
的条件。
引理3.2 在任意环R上,
。
证明 设
。则存在投射R-模的正合列
其中
且对任意的Level R-模L,有
正合。由( [10],命题2.7)知,对任意的绝对clean右R-模A,有
正合。又因为内射R-模一定是绝对clean R-模,所以对任意的内射右R-模I,有
正合。因此
。
定理3.3 若R是凝聚环,则
。
证明 由定义知,
。设
。则存在投射R-模的正合列
其中
且对任意的平坦R-模F,有
正合。又因为R是凝聚环。由( [8],推论2.11)知,Level R-模是平坦R-模,所以对任意的Level R-模L,有
正合。因此
。故
。又由引理3.2和( [7],推论1)知,
,
。因此
。
命题3.4
当且仅当
。
证明 必要性:由定义知,
,而
,所以
。
充分性:由定义知,
。设
。则存在投射R-模的正合列
其中
且有
。因为
,所以对任意的Level R-模L,有
。因此对任意的Level R-模L,
正合。故
。
推论3.5 设R是凝聚环。则
当且仅当
。
证明 必要性:由定理3.3知,
。因为
,所以
。又因为
,所以
。
充分性:因为R是凝聚环,所以由定理3.3知,
。又因为
,所以由命题3.4,得
。
定理3.6 设R是凝聚环。则下列条件等价:
1)
。
2)
。
3) 对任意的R-模
,有
。
4)
。
证明 2) ⟹ 1) 因为
,而
,所以
。
1) ⟹ 2) 由定义知, 。下证
。下证 。设M是强Gorenstein投射模。则存在投射R-模的正合列
。设M是强Gorenstein投射模。则存在投射R-模的正合列
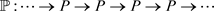
其中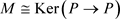 。由假设知,
。由假设知, ,所以对任意的内射右R-模I,有
,所以对任意的内射右R-模I,有 。又因为有短正合列
。又因为有短正合列 ,所以对任意的内射右R-模A,有正合列
,所以对任意的内射右R-模A,有正合列
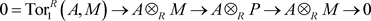
所以 正合。因此
正合。因此 。设
。设 。因为
。因为 是强Gorenstien投射模的直和项且投射余可解的Gorenstien平坦模的类关于直和项封闭,所以
是强Gorenstien投射模的直和项且投射余可解的Gorenstien平坦模的类关于直和项封闭,所以 。又因为R是凝聚环,由定理3.3知,
。又因为R是凝聚环,由定理3.3知, ,所以
,所以 。
。
1) ⇔ 3) 由( [11],定理2.2)可得。
3) ⟹ 4) 设 。因为
。因为 ,所以对任意的内射右R-模I,有
,所以对任意的内射右R-模I,有 。又因为
。又因为 ,所以
,所以 。
。
4) ⟹ 3) 设 。则存在投射R-模的正合列
。则存在投射R-模的正合列
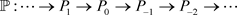
其中 。从而有正合列
。从而有正合列
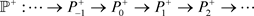
且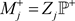 。因为
。因为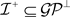 ,所以对任意的内射右R-模I,有
,所以对任意的内射右R-模I,有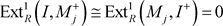 。因此
。因此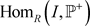 正合。故
正合。故 。
。
下面我们讨论模的Gorenstein AC投射预覆盖的存在性。
引理3.7 设R是凝聚环。若 ,则存在特殊的Gorenstein AC投射预覆盖
,则存在特殊的Gorenstein AC投射预覆盖 ,其中
,其中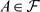 。
。
证明 因为由( [12],定理2.13)知,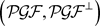 是完全的余挠对,所以存在短正合列
是完全的余挠对,所以存在短正合列
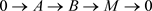
其中 ,
, 。又因为
。又因为 且
且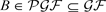 ,所以
,所以 。因此
。因此 。由( [6],定理4.11)知,
。由( [6],定理4.11)知, 。又因为R是凝聚环,所以对上述短正合列,由定理3.3知,
。又因为R是凝聚环,所以对上述短正合列,由定理3.3知,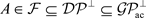 且
且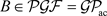 。从而得
。从而得 是M的一个特殊的Gorenstein AC投射预覆盖。
是M的一个特殊的Gorenstein AC投射预覆盖。
设 是环。我们记
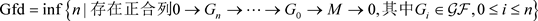
且称之为R-模M的Gorenstein平坦维数。
命题3.8 设R是凝聚环。则每一个Gorenstein平坦维数有限的模都有一个特殊的Gorenstein AC投射预覆盖。
证明 设M的Gorenstein平坦维数有限。则由( [9],引理3.17)知,存在短正合列
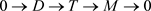
其中 且D的平坦维数有限。对T,由引理3.7知,T有一个特殊的Gorenstein AC投射预覆盖,即存在正合列
且D的平坦维数有限。对T,由引理3.7知,T有一个特殊的Gorenstein AC投射预覆盖,即存在正合列
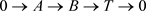
其中 且
且 。从而有拉回图
。从而有拉回图
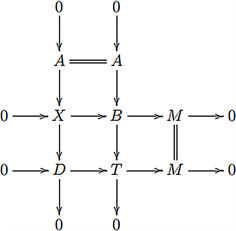
所以 正合,其中
正合,其中 。又因为D的平坦维数有限且
。又因为D的平坦维数有限且 ,所以X的平坦维数有限。因此
,所以X的平坦维数有限。因此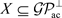 。故
。故 是M的一个特殊的Gorenstein AC投射预覆盖。
是M的一个特殊的Gorenstein AC投射预覆盖。
基金项目
国家自然科学基金项目(11761060)。
参考文献