求解一维对流扩散方程的高阶方法

High-Order Methods for Solving One-Dimensional Convection-Diffusion Equations

摘要: 本文提出了一类求解一维对流扩散方程的埃尔米特插值的加权本质无振荡格式，称为HWENO (Hermite WENO)格式。这类格式的主要优点是在光滑区域内实现高阶精度，在间断处能够保持强间断性且无振荡。本文将对流扩散方程中对流项采用HWENO格式去求解，为了保证格式的紧性和高阶精度，扩散项采用三点的埃尔米特插值去近似得到，首先将方程写成守恒的半离散形式。格式的构造中，空间项基于有限体积形式的高精度Hermite重构，时间项采用非线性稳定的Runge-Kutta方法推进。大量的数值结果验证了本文格式的有效性和稳定性。

Abstract: In this paper, a class of weighted essentially non-oscillatory (WENO) schemes of Hermite interpolation, termed HWENO (Hermite WENO) schemes, for solving one-dimension convection-diffusion equations is presented. The main advantage of the schemes is their capability to achieve high order formal accuracy in smooth regions while maintaining stable, nonoscillatory and sharp discontinuity transitions. In this paper, the convection term in the convection-diffusion equation is solved by the HWENO scheme. In order to ensure the compactness and high order accuracy of the scheme, the diffusion term is approximated by the three-point Hermite interpolation. Firstly, the equation is written into a conserved semi-discrete form. The constructed spatial term was based on the high order accuracy Hermite interpolation, finite volume formulation, and the time term was advanced by using the nonlinearly stable Runge-Kutta method. A large number of numerical results verify the validity and stability of the proposed scheme.

1. 引言

对流扩散方程所涉及的物理模型在许多的领域有着广泛的应用。例如气体动力学、石油勘探等方面。对于这类方程的求解方法虽然也有不少，但当求解的问题背景带有间断时，其他方法就显得顾此失彼了。因此设计准确有效的方法来解决这些问题是相当重要的，并且已经吸引了许多研究人员和实践者的兴趣。为了解决这一问题，近几十年来发展了许多高阶数值方法 [1] [2] [3] [4]。1987年Harten等人提出了有限体积ENO格式 [5]，它使用一个基于局部光滑的自适应模板，从而在函数光滑的地方产生高阶精度。之后，刘旭东等人在1994年提出了一个高阶WENO格式 [6] [7]，不再仅使用一个候选模板，而是使用所有候选模板的线性凸组合。在没破坏间断点附近的非振荡行为的情况下，还使数值通量的精度提高了一阶。2004年，邱建贤和舒其望根据WENO的重构思想，提出了一类Hermite WENO (HWENO)格式 [8]，其重构过程需要原函数值及其一阶导数值，而原始的WENO格式只需原函数值参与重构。相比较WENO格式而言，HWENO格式为更紧致的一类格式，具有紧性。之后将HWENO格式推广到求解二维守恒律 [9] 和Hamilton-Jacobi [10] 方程。而本文的FVM-HWENO方法思想来源于求解带间断问题的双曲方程，即在问题的光滑处可以达到高阶精度，在问题的间断处可以有很好的陡峭的过度，是处理带有间断问题的一类较满意的数值方法。而且之前的文献 [11] - [16] 对于数值格式的研究大都考虑双曲问题，对于其他类型的方程研究较少，本文将HWENO方法用于求解对流扩散方程的对流项，扩散项采用三点的埃尔米特插值去近似，提出了适合这类方程的数值格式。

本文基于FVM-HWENO方法，推导了对流扩散方程的数值求解格式，且在光滑处保持高阶精度，间断处保持无振荡，数值实验证明了本文格式对求解带间断和强激波的对流扩散方程的有效性。

2. 数值格式

考虑一维情况下的对流扩散方程：

$\{\begin{array}{l}{u}_t+f{\left(u\right)}_x=a{\left(u\right)}_{xx},x\in \left(-\infty ,\infty \right),t\in \left(0,\infty \right),\hfill \\ u\left(x,0\right)=u_0\left(x\right),x\in \left(-\infty ,\infty \right).\hfill \end{array}$ (1)

为简便化，计算在均匀网格上进行，若记 $x_i$ 为计算的网格节点， $I_i=\left\{x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}\right\}$ 表示计算单元，则网格步长为 $\Delta x=x_{i+1}-x_i$，网格单元中心为 $x_{i+\frac{1}{2}}=1/2\left(x_i+x_{i+1}\right)$。

令 $v=u_x,b\left(u,v\right)=a{\left(u\right)}_x=a^{\prime }\left(u\right)v,g\left(u,v\right)=f{\left(u\right)}_x=f^{\prime }\left(u\right)v$，在方程(1)两端对x求导数，得如下方程：

$\{\begin{array}{ll}{u}_t+f{\left(u\right)}_x=a{\left(u\right)}_{xx},\hfill & u\left(x,0\right)=u_0\left(x\right),\hfill \\ v_t+g{\left(u,v\right)}_x=b{\left(u,v\right)}_{xx},\hfill & v\left(x,0\right)=v_0\left(x\right).\hfill \end{array}$

定义 $u$ 和 $v$ 的单元平均值：

$\{\begin{array}{c}{\bar{u}}_i\left(t\right)=\frac{1}{\Delta x}{\displaystyle {\int }_{I_i}u\left(x,t\right)\text{d}x,}\\ {\bar{v}}_i\left(t\right)=\frac{1}{\Delta x}{\displaystyle {\int }_{I_i}v\left(x,t\right)\text{d}x.}\end{array}$

对(1)式在单元 $I_i$ 上积分化简得到一个对流扩散方程(1)的等价形式为：

$\{\begin{array}{l}\frac{\text{d}{\bar{u}}_i\left(t\right)}{\text{d}t}=-\frac{1}{\Delta x}\left[\left(f\left(u\left(x_{i+\frac{1}{2}},t\right)\right)\right)-\left(f\left(u\left(x_{i-\frac{1}{2}},t\right)\right)\right)\right]+\frac{1}{\Delta x}{\displaystyle {\int }_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}a{\left(u\right)}_x\text{d}x,}\hfill \\ \frac{\text{d}{\bar{v}}_i\left(t\right)}{\text{d}t}=-\frac{1}{\Delta x}\left[\left(g\left(u\left(x_{i+\frac{1}{2}},t\right),v\left(x_{i+\frac{1}{2}},t\right)\right)\right)-\left(g\left(u\left(x_{i-\frac{1}{2}},t\right),v\left(x_{i-\frac{1}{2}},t\right)\right)\right)\right]+\frac{1}{\Delta x}{\displaystyle {\int }_{i-\frac{1}{2}}^{x_{i+\frac{1}{2}}}b{\left(u,v\right)}_x\text{d}x,}\hfill \end{array}$

则可得微分方程(1)的半离散形式为：

$\{\begin{array}{c}\frac{\text{d}{\bar{u}}_i\left(t\right)}{\text{d}t}=-\frac{1}{\Delta x}\left({\hat{f}}_{i+\frac{1}{2}}-{\hat{f}}_{i-\frac{1}{2}}\right)+a_i\left(t\right),\\ \frac{\text{d}{\bar{v}}_i\left(t\right)}{\text{d}t}=-\frac{1}{\Delta x}\left({\hat{g}}_{i+\frac{1}{2}}-{\hat{g}}_{i-\frac{1}{2}}\right)+b_i\left(t\right),\end{array}$ (2)

称 ${\hat{f}}_{i+\frac{1}{2}}$ 和 ${\hat{g}}_{i+\frac{1}{2}}$ 为数值通量，它们需要满足数值通量条件：Lipschitz-连续和相容性。这里我们使用Lax-Friedrichs通量 [17]：

$\{\begin{array}{l}{\hat{f}}_{i+\frac{1}{2}}=\frac{1}{2}\left[f\left(u_{i+\frac{1}{2}}^{-}\right)+f\left(u_{i+\frac{1}{2}}^{+}\right)-\alpha \left(u_{i+\frac{1}{2}}^{+}-u_{i+\frac{1}{2}}^{-}\right)\right],\\ {\hat{g}}_{i+\frac{1}{2}}=\frac{1}{2}\left[g\left(u_{i+\frac{1}{2}}^{-},v_{i+\frac{1}{2}}^{-}\right)+g\left(u_{i+\frac{1}{2}}^{+},v_{i+\frac{1}{2}}^{+}\right)-\alpha \left(v_{i+\frac{1}{2}}^{+}-v_{i+\frac{1}{2}}^{-}\right)\right].\end{array}$

其中 $\alpha ={\max }_{u\in D}\left|f^{\prime }\left(u\right)\right|,D=\left[\min \left(a,b\right),\max \left(a,b\right)\right]$。

为了保证整个空间方向的精度，本文采用三点的埃尔米特插值去近似扩散项：

$a_i=\frac{5}{4\Delta x^2}{\bar{u}}_{i-1}-\frac{1}{\Delta x^2}{\bar{u}}_i-\frac{1}{4\Delta x^2}{\bar{u}}_{i+1}+\frac{1}{2\Delta x}{\bar{v}}_{i-1}+\frac{1}{\Delta x}{\bar{v}}_{i+1},$

$b_i=\frac{3}{16\Delta x}{\bar{u}}_{i-1}-\frac{3}{2\Delta x}{\bar{u}}_i+\frac{21}{16\Delta x}{\bar{u}}_{i+1}+\frac{1}{16}{\bar{v}}_{i-1}-\frac{3}{16}{\bar{v}}_{i+1}.$

使用三阶TVD Runge-Kutta [18] 对常微分方程(2)进行时间上的离散

$\{\begin{array}{l}{\bar{u}}^{\text{(1)}}={\bar{u}}^n+\Delta tL\left({\bar{u}}^n\right),\\ {\bar{u}}^{\text{(2)}}=\frac{3}{4}{\bar{u}}^n+\frac{1}{4}{\bar{u}}^{\text{(1)}}+\frac{1}{4}\Delta tL\left({\bar{u}}^{\text{(1)}}\right),\\ {\bar{u}}^{\text{(3)}}=\frac{1}{3}{\bar{u}}^n+\frac{2}{3}{\bar{u}}^{\text{(2)}}+\frac{2}{3}\Delta tL\left({\bar{u}}^{\text{(2)}}\right).\end{array}$

有限体积HWENO格式重要的部分是根据单元平均值 $\left\{{\bar{u}}_i,{\bar{v}}_i\right\}$ 计算点值 $\left\{u_{i+\frac{1}{2}}^{\pm },v_{i+\frac{1}{2}}^{\pm }\right\}$ 的重构，这个重构过程还要保证格式的高阶精度和本质无振荡性质。下面分别给出 $u_{i+\frac{1}{2}}^{\pm }$, $v_{i+\frac{1}{2}}^{\pm }$ 的HWENO重构步骤。

2.1. 根据单元平均值 $\left\{{\bar{u}}_i,{\bar{v}}_i\right\}$，由HWENO方法重构 $u_{i+\frac{1}{2}}^{\pm }$ 的步骤

1) 给定三个小模板 $S_0=\left\{I_{i-1},I_i\right\},S_1=\left\{I_i,I_{i+1}\right\},S_2=\left\{I_{i-1},I_i,I_{i+1}\right\}$ 和一个大模板 $T=\left\{I_{i-1},I_i,I_{i+1}\right\}=S_0\cup S_1\cup S_2,$ 在集合 $S_0,S_1,S_2,T$ 上分别重构三个二次多项式 $p_0\left(x\right),p_1\left(x\right),p_2\left(x\right)$ 和一个四次多项式 $q\left(x\right)$，其分别满足下面的条件：

$\frac{1}{\Delta x}{\displaystyle {\int }_{{{\displaystyle I}}_{i+j}}{p}_0\left(x\right)}\text{d}x={\bar{u}}_{i+j},j=-1,0,\frac{1}{\Delta x}{\displaystyle {\int }_{I_{i-1}}{p^{\prime }}_0\left(x\right)}\text{d}x={\bar{v}}_{i-1};$

$\frac{1}{\Delta x}{\displaystyle {\int }_{I_{i+j}}{p}_1}\left(x\right)\text{d}x={\bar{u}}_{i+j},j=0,1,\frac{1}{\Delta x}{\displaystyle {\int }_{I_{i+1}}{p^{\prime }}_1\left(x\right)}\text{d}x={\bar{v}}_{i+1};$

$\frac{1}{\Delta x}{\displaystyle {\int }_{I_{i+j}}{p}_2}\left(x\right)\text{d}x={\bar{u}}_{i+j}\text{,}j=-1,0,1;$

$\frac{1}{\Delta x}{\displaystyle {\int }_{I_{i+j}}q\left(x\right)}\text{d}x={\bar{u}}_{i+j},j=-1,0,1,\frac{1}{\Delta x}{\displaystyle {\int }_{I_{i+j}}{q}^{\prime }\left(x\right)}\text{d}x={\bar{v}}_{i+j}.$

经计算，这些多项式在单元边界 $x_{i+\frac{1}{2}}$ 处的值可表示为：

$p_0\left(x_{i+\frac{1}{2}}\right)=-\frac{7}{6}{\bar{u}}_{i-1}+\frac{13}{6}{\bar{u}}_i-\frac{2\Delta x}{3}{\bar{v}}_{i-1},$

$p_1\left(x_{i+\frac{1}{2}}\right)=\frac{5}{6}{\bar{u}}_{i+1}+\frac{1}{6}{\bar{u}}_i-\frac{\Delta x}{3}{\bar{v}}_{i+1},$

$p_2\left(x_{i+\frac{1}{2}}\right)=-\frac{1}{6}{\bar{u}}_{i-1}+\frac{5}{6}{\bar{u}}_i+\frac{1}{3}{\bar{u}}_{i+1},$

$q\left(x_{i+\frac{1}{2}}\right)=-\frac{23}{120}{\bar{u}}_{i-1}+\frac{19}{30}{\bar{u}}_i+\frac{67}{120}{\bar{u}}_{i+1}-\Delta x\left(\frac{3}{40}{\bar{v}}_{i-1}+\frac{7}{40}{\bar{v}}_{i+1}\right).$

2) 求线性权 ${\gamma }_0,{\gamma }_1,{\gamma }_2$，满足：

$q\left(x_{i+\frac{1}{2}}\right)={\displaystyle \underset{j=0}{\overset{2}{\sum }}{\gamma }_j}{p}_j\left(x_{i+\frac{1}{2}}\right),$

对于在大模板上的所有的 $u$ 和 $v$ 的单元平均值都成立且满足 ${\displaystyle {\sum }_{j=0}^2{\gamma }_j}=1$。从而可得：

${\gamma }_0=\frac{9}{80},{\gamma }_1=\frac{21}{40},{\gamma }_2=\frac{29}{80}.$

3) 计算光滑指示子 ${\beta }_j$。光滑指示子是用来反映插值函数 $p_j\left(x\right)$ 在所在目标单元 $I_i$ 上的光滑程度。这里采用文献 [7] 的光滑指示子的表达形式：

${\beta }_j={\displaystyle \underset{l=1}{\overset{2}{\sum }}{\displaystyle {\int }_{I_i}\Delta x^{2l-1}}}{\left(\frac{{\partial }^l}{\partial x^l}{p}_j\left(x\right)\right)}^2\text{d}x.$

本文中，通过计算求得：

$\begin{array}{l}{\beta }_0={\left(-2{\bar{u}}_{i-1}+2{\bar{u}}_i-\Delta x{\bar{v}}_{i+1}\right)}^2+\frac{13}{3}{\left(-{\bar{u}}_{i-1}+{\bar{u}}_i-\Delta x{\bar{v}}_{i-1}\right)}^2,\\ {\beta }_1={\left(-2{\bar{u}}_i+2{\bar{u}}_{i+1}-\Delta x{\bar{v}}_{i+1}\right)}^2+\frac{13}{3}{\left({\bar{u}}_i-{\bar{u}}_{i+1}+\Delta x{\bar{v}}_{i+1}\right)}^2,\\ {\beta }_2=\frac{1}{4}{\left(-{\bar{u}}_{i-1}+{\bar{u}}_{i+1}\right)}^2+\frac{13}{12}{\left({\bar{u}}_{i-1}-2{\bar{u}}_i+{\bar{u}}_{i+1}\right)}^2.\end{array}$

4) 计算非线性权。

${\omega }_j=\frac{{\bar{\omega }}_k}{{\displaystyle {\sum }_{k=0}^2{\bar{\omega }}_k}},{\bar{\omega }}_k=\frac{{\gamma }_k}{{\left(\epsilon +{\beta }_k\right)}^2}\text{,}j,k=0,1,2,$

这里 ${\gamma }_k$ 是2)中的线性权， $\epsilon$ 是一个事先给定的非常小的正数，避免分母变为0，本文计算中取 $\epsilon ={10}^{-6}$。最后可计算出 $u_{i+\frac{1}{2}}^{-}$ 的HWENO重构表达形式为：

$u_{i+\frac{1}{2}}^{-}\approx {\displaystyle \underset{j=0}{\overset{2}{\sum }}{\omega }_j{p}_j}\left(x_{i+\frac{1}{2}}\right).$

对于 $u_{i+\frac{1}{2}}^{+}$ 的重构过程与上面的 $u_{i+\frac{1}{2}}^{-}$ 的重构过程关于单元边界 $x_{i+\frac{1}{2}}$ 成镜面对称的，可由上述步骤类似得到。

2.2. 根据单元平均值 $\left\{{\bar{u}}_i,{\bar{v}}_i\right\}$，由HWENO方法重构 $v_{i+\frac{1}{2}}^{\pm }$ 的步骤

1) 同样给定三个小模板 $S_0=\left\{I_{i-1},I_i\right\},S_1=\left\{I_i,I_{i+1}\right\},S_2=\left\{I_{i-1},I_i,I_{i+1}\right\}$ 和一个大模板 $T=\left\{I_{i-1},I_i,I_{i+1}\right\}=S_0\cup S_1\cup S_2,$ 在集合 $S_0,S_1,S_2,T$ 上分别重构三个三次多项式 $p_0\left(x\right),p_1\left(x\right),p_2\left(x\right)$ 和一个五次多项式 $q\left(x\right)$，分别满足条件：

$\frac{1}{\Delta x}{\displaystyle {\int }_{I_{i+j}}{p}_0\left(x\right)}\text{d}x={\bar{u}}_{i+j},\frac{1}{\Delta x}{\displaystyle {\int }_{I_{i+j}}{p^{\prime }}_0\left(x\right)}\text{d}x={\bar{v}}_{i+j},j=-1,0;$

$\frac{1}{\Delta x}{\displaystyle {\int }_{I_{i+j}}{p}_1}\left(x\right)\text{d}x={\bar{u}}_{i+j},\frac{1}{\Delta x}{\displaystyle {\int }_{I_{i+j}}{p^{\prime }}_1\left(x\right)}\text{d}x={\bar{v}}_{i+j},j=0,1;$

$\frac{1}{\Delta x}{\displaystyle {\int }_{I_{i+j}}{p}_2}\left(x\right)\text{d}x={\bar{u}}_{i+j},j=-1,0,1,\frac{1}{\Delta x}{\displaystyle {\int }_{I_i}{p^{\prime }}_2\left(x\right)}\text{d}x={\bar{v}}_i;$

$\frac{1}{\Delta x}{\displaystyle {\int }_{I_{i+j}}q\left(x\right)}\text{d}x={\bar{u}}_{i+j},\frac{1}{\Delta x}{\displaystyle {\int }_{I_{i+j}}{q}^{\prime }\left(x\right)}\text{d}x={\bar{v}}_{i+j},j=-1,0,1.$

经计算，这些多项式的一阶导数在单元边界 $x_{i+\frac{1}{2}}$ 处的值可表示为：

${p^{\prime }}_0\left(x_{i+\frac{1}{2}}\right)=\frac{4}{\Delta x}\left({\bar{u}}_{i-1}-{\bar{u}}_i\right)+\frac{3}{2}{\bar{v}}_{i-1}+\frac{7}{2}{\bar{v}}_i,$

${p^{\prime }}_1\left(x_{i+\frac{1}{2}}\right)=-\frac{2}{\Delta x}\left(-{\bar{u}}_{i+1}+{\bar{u}}_i\right)-\frac{1}{2}{\bar{v}}_i-\frac{1}{2}{\bar{v}}_{i+1},$

${p^{\prime }}_2\left(x_{i+\frac{1}{2}}\right)=\frac{1}{4\Delta x}\left({\bar{u}}_{i-1}-4{\bar{u}}_i+3{\bar{u}}_{i+1}\right)+\frac{1}{2}{\bar{v}}_i,$

$q^{\prime }\left(x_{i+\frac{1}{2}}\right)=\frac{1}{\Delta x}\left(\frac{1}{4}{\bar{u}}_{i-1}-2{\bar{u}}_i+\frac{7}{4}{\bar{u}}_{i+1}\right)+\frac{1}{12}{\bar{v}}_{i-1}-\frac{1}{6}{\bar{v}}_i-\frac{5}{12}{\bar{v}}_{i+1}.$

2) 计算线性权 ${{\gamma }^{\prime }}_0,{{\gamma }^{\prime }}_1,{{\gamma }^{\prime }}_2$。由：

$q^{\prime }\left(x_{i+\frac{1}{2}}\right)={\displaystyle \underset{j=0}{\overset{2}{\sum }}{{\gamma }^{\prime }}_j}{p^{\prime }}_j\left(x_{i+\frac{1}{2}}\right),$

则

${{\gamma }^{\prime }}_0=\frac{1}{18},{{\gamma }^{\prime }}_1=\frac{5}{6},{{\gamma }^{\prime }}_2=\frac{1}{9}.$

3) 计算光滑指示子。导数的光滑指示子的定义如下：

${{\beta }^{\prime }}_j={\displaystyle \underset{l=2}{\overset{3}{\sum }}{\displaystyle {\int }_{I_i}\Delta x^{2l-1}}}{\left(\frac{{\partial }^l}{\partial x^l}{p}_j\left(x\right)\right)}^2\text{d}x.$

因为重构的是函数的一阶导数值而不是函数值，因此求和从二阶导数开始。经计算，本文中光滑指示子的表达式可写为：

${{\beta }^{\prime }}_0=4{\left(3{\bar{u}}_{i-1}-3{\bar{u}}_i+\Delta x{\bar{v}}_{i-1}+2\Delta x{\bar{v}}_i\right)}^2+39{\left(2{\bar{u}}_{i-1}-2{\bar{u}}_i+\Delta x{\bar{v}}_{i-1}+\Delta x{\bar{v}}_i\right)}^2,$

${{\beta }^{\prime }}_1=4{\left(-3{\bar{u}}_i+3{\bar{u}}_{i+1}-\Delta x{\bar{v}}_{i+1}-2\Delta x{\bar{v}}_i\right)}^2+39{\left(2{\bar{u}}_i-2{\bar{u}}_{i+1}+\Delta x{\bar{v}}_{i+1}+\Delta x{\bar{v}}_i\right)}^2,$

${{\beta }^{\prime }}_2={\left({\bar{u}}_{i-1}-2{\bar{u}}_i+{\bar{u}}_{i+1}\right)}^2+\frac{39}{4}{\left(-{\bar{u}}_{i-1}-2\Delta x{\bar{v}}_i+{\bar{u}}_{i+1}\right)}^2.$

4) 计算非线性权，利用：

${{\omega }^{\prime }}_j=\frac{{\bar{\omega }}^{\prime }{}_k}{{\displaystyle {\sum }_{k=0}^2{\bar{\omega }}^{\prime }{}_k}},{\bar{\omega }}^{\prime }{}_k=\frac{{{\gamma }^{\prime }}_k}{{\left(\epsilon +{{\beta }^{\prime }}_k\right)}^2}\text{,}j,k=0,1,2.$

最后，基于HWENO重构的 $v_{i+\frac{1}{2}}^{-}$ 为：

$v_{i+\frac{1}{2}}^{-}\approx {\displaystyle \underset{j=0}{\overset{2}{\sum }}{{\omega }^{\prime }}_j{p^{\prime }}_j}\left(x_{i+\frac{1}{2}}\right).$

同样地，利用镜面对称，可求出 $v_{i+\frac{1}{2}}^{+}$ 的重构。

将重构得到的 $u_{i+\frac{1}{2}}^{\pm },v_{i+\frac{1}{2}}^{\pm }$ 代入通量中，此时(2)式即化为常微分方程，最后通过TVD Runge-Kutta法进行时间上的离散。

3. 数值结果

3.1. 算例3.1一维精度测试

这部分我们给出了大量的数值算例，通过算例说明HWENO格式的性质和算法的稳定性和有效性。数值实验均在Matlab 2018a环境中执行。

求解线性对流扩散方程：

$\{\begin{array}{l}{u}_t+u_x=\epsilon u_{xx},\\ u\left(x,0\right)=u_0\left(x\right),\end{array}0\le x\le 2\text{π},t>0.$

问题的初始解为 $u\left(x,0\right)=\sin \left(x\right)$，且在计算区域取周期边界条件。精确解为 $u\left(x,t\right)={\text{e}}^{-\epsilon t}\sin \left(x-t\right)$。这里我们取 $\epsilon =0.01$，时间计算到 $t=1$。表1的数据结果显示本文的数值格式达到了五阶精度。

Table 1. Error and accuracy of HWENO schemes

表1. HWENO格式的误差和精度阶

3.2. 算例3.2非线性Burgers方程 [19]

$\{\begin{array}{l}{u}_t+{\left(u^2/2\right)}_x=\epsilon u_{xx},\\ u\left(x,0\right)=u_0\left(x\right),\end{array}0\le x\le 2,t>0.$

该问题在区间 $\left[0,2\right]$ 上满足边界条件 $u\left(0,t\right)=u\left(2,t\right)=0$。取 $\epsilon =0.01,\alpha =2$，最终时间计算到 $t=1$。初始值为：

$u\left(x,0\right)=2\text{π}\epsilon \frac{\sin \left(\text{π}x\right)}{\alpha +\cos \left(\text{π}x\right)},$

该问题的精确解被给出：

$u\left(x,t\right)=2\text{π}\epsilon \frac{\exp \left(-{\text{π}}^2\epsilon t\right)\sin \left(\text{π}x\right)}{\alpha +\exp \left(-{\text{π}}^2\epsilon t\right)\cos \left(\text{π}x\right)}.$

图1画出了该方程在网格为100的时候和精确解的数值结果。可以清楚地看到，数值计算结果与精确解吻合的很好。

3.3. 算例3.3 Buckley-Leveret方程的求解

求解Buckley-Leveret方程 [20]：

$\{\begin{array}{l}{u}_t+f{\left(u\right)}_x=\epsilon {\left(v\left(u\right)u_x\right)}_x,\\ u\left(x,0\right)=u_0\left(x\right),\end{array}0\le x\le 1,t>0.$

数值解计算到 $t=0.2$，取 $\epsilon =0.01$，边界条件为常值边界条件即 $u\left(0,t\right)=1$。 $v\left(u\right)$ 和初始条件为：

$v\left(u\right)=\{\begin{array}{c}4u\left(1-u\right),0\le u\le 1\\ 0,其他\end{array},$

$u\left(x,0\right)=\{\begin{array}{c}1-3x,0\le x\le 1/3\\ 0,1/3\le x\le 1\end{array}.$

流通量为： $f\left(u\right)=\frac{u^2}{u^2+{\left(1-u\right)}^2}.$

图2画出了数值解与800个网格点的解作为参考解之间的数值结果，从结果可以看出在间断处基本无振荡。

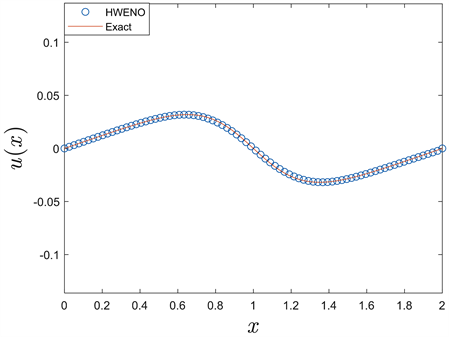
Figure 1. Numerical simulation of Burgers equation

图1. Burgers方程的数值模拟

Figure 2. Numerical simulation of Buckley-Leveret equation

图2. Buckley-Leveret方程的数值模拟

4. 总结

本文求解了对流扩散方程，对流项采用五阶HWENO方法重构，扩散项采用了三点的埃尔米特插值，时间上采用经典的总变差有界的三阶Runge-Kutta方法推进。本文的难点在于，方程的解既要达到高精度，保证格式的紧性，又要实现无振荡性质。结合方程的特点，我们这里也给出了较好的数值离散方法，这个方法构造简单，也比较容易实现。最后大量的数值算例验证了该方法的精度和本质无振荡性质。