1. 介绍
由于随机扰动在现实中无处不在,因此随机模型在机械系统、生物系统、传感器网络和道路交通网络中得到了广泛的应用 [1]。在过去的十年中,许多学者研究了随机系统的控制和过滤,并获得了许多成就。开发的滤波方法通常用于各种系统,例如非线性系统和不确定的时滞系统 [2] [3]。传感器信息融合估计器的设计网络多传感器融合中的无线传输系统引起了广泛的研究兴趣,基本的流程图如图1所示,即通过通信网络连接到融合中心。与传统的融合系统相比,通信网络具有维护方便,成本低,安装简单的优点。但是,当分布式传感器在通信网络中不够完善时,数据包丢失和传输延迟是不可避免的。这些是导致融合估算器性能下降的主要原因,并且可能会降低原始融合标准。

Figure 1. Multi-sensor fusion estimation
图1. 多传感器融合估计
从控制理论的角度来看,近年来,控制器和滤波器的设计已成为研究重点 [4]。时变控制器/滤波器已在文献 [5] 中进行了设计,它由一个常数矩阵和可以实时测量的时变参数组成 [5]。通过解决一组线性矩阵不等式,常数矩阵可以很容易地获得。此外,它比仅具有固定常数的传统滤波器性能要保守一些。在过去的几年中,在离散时间和连续时间系统中都广泛地研究了增益调度滤波问题。在最近,一般借助于含有参数的李雅普诺夫函数法解决增益调度的过滤/控制问题来实现更好的过滤/控制性能的问题 [6],并且在过去的工作中已经提出了一些相关的成果。对于具有随机损耗现象的离散非线性随机系统 [7],对于具有随机丢失现象的离散非线性随机系统,尤其是当系统的时变特性主要由随机丢失现象导致时,这种问题很少研究过。因此,这确实是一个具有挑战性的问题,它值得进行大量的研究。但是,加权与损失概率有关的调度过滤问题SN从未针对非线性随机系统进行过研究。
本文研究了遗漏概率相关性离散时间的加权调度过滤问题系统。本文的主要贡献有三个方面:1) 考虑加权调度过滤问题应用于一般的离散时间随机非线性系统;2) 通过使用时间建立新的执行器模型满足伯努利随机变量的序列变化分配;3) 根据融合估计算法获得了一类新的滤波器增益。
2. 问题描述
我们考虑如下的非线性随机系统:
式(1)
测量输出为:
式(2)
其中
是目标状态,
是汇聚节点i的测量输出,
和
遵从独立同分布。B、
、D是具有合适维度的已知矩阵,
是一个表示传感器数据丢失的概率符合以下伯努利分布随机白序列
式(3)
其中标量序列
属于区间
,
和
分别是
的下界和上界。在本文中,假设
,
和
是不相关的,此外,一类符合概率分布定律(4.3)的丢失测量时允许存在的。
向量值函数
代表非线性分布,且满足如下的扇形有界分布
式(4)
其中初始条件为
,且
是一个正定矩阵,
和
是维数适当的常数矩阵,一般情况下,
在区间
上取值,在这种情况下,非线性函数
可以转换成一个线性部分和一个非线性部分。
式(5)
结合式(4)和式(5),可得:
式(6)
基于测量输出
,第i个节点的局部估计器可以写作
式(7)
设置
是可求的估计器增益,定义局部估计误差为
和
,那么第i个节点的局部估计误差计算可得:
式(8)
定义
和
,那么第i个节点的局部估计误差系统可写为:
式(9)
其中
因此,当把局部估计送到融合中心,融合估计
可得到:
式(10)
其中
是用以下形式组成的加权调度序列
式(11)
其中
和
是一定维数的常数矩阵,且
是随时间变化的丢失概率,可以过统计测试实时衡量。设置
,
和
,加权调度的融合估计误差为
,可得:
式(12)
定义
和
。根据式(10)~式(12),加权调度融合估计误差系统可写为:
式(13)
其中
定义1:如果存在条件
和
使得下列不等式成立,那么滤波融估计误差系统在均方意义下是稳定的。
式(14)
本文的目的是为离散时间随机系统(12)设计一个满意的滤波器,其中允许非线性、随机干扰和丢失测量。
3. 最终结果
在以下定理中,利用凸优化方法和参数相关的Lyapunov函数用于处理离散随机系统(13)的加权调度融合估计问题。
定理1:考虑离散时间随机滤波融合估计误差系统(13),如果存在正定矩阵序列
,且满足如下线性矩阵不等式:
式(15)
其中
那么加权调度的融合误差系统是均方稳定的。
证明:为了验证每个估计误差动态(9)和融合误差动态(13)是渐近均方稳定的。构造以下Lyapunov函数
式(16)
计算
的差分并对其取数学期望,可得:
根据式(5)和式(6),且有
,上述不等式可以写为:
其中
,并且有:
其中
由Schur引理可得:
式(17)
且有式(17)与下式相等
式(18)
我们将显示
,很容易得到
,(12)通过左乘对角阵
,我们可得
其中
然后根据不等式
可得:
式(19)
其中
,再根据Schur引理很容易得到
,
式(20)
其中
是向量范数且
是Q的特征值。根据引理1,加权融合误差系统是均方稳定的。证毕。
注2:在定理1中,为了增强设计滤波器的性能,提出了一个时空Lyapunov函数,该函数取决于未命中概率。值得注意的是,在过去的几年中,为了减少保守性,依赖于参数的Lyapunov函数已被广泛用于处理时变和不确定的参数系统。
定理2:考虑融合估计误差系统(13),如果存在正定矩阵
和
,松弛矩阵S以及下列线性矩阵不等式成立:
式(21)
其中i, j和
,局部估计器增益
和加权调度矩阵为
,
,其中:
然后,可以获取加权调度滤波器以确保融合估计误差系统均方稳定
证明:首先设置
式(22)
我们有
式(23)
其中
和
。
同样,定义
式(24)
很容易得到下列不等式
式(25)
其中
。
通过前面定义的转换,可以轻松推断出
另外一方面,根据式(22),可得:
式(26)
根据式(22)~(25),可推断出不等式(15)是成立的,根据定理1和2,融合估计算法如表1所示:

Table 1. The fusion estimation x ^ ( t ) algorithm
表1. 融合估计
的算法程序
4. 数值仿真实例
在本章节中,通过一个数值示例来验证所提出方法的有效性。针对具有随机发生的非线性的离散时间随机系统设计加权调度估计器。取目标系统的参数分别为:
设置时变的伯努利分布序列为
,和扇形非线性函数
为:
满足等式(4.5),且设置初始值为
,根据算法1,局部估计器增益
,
,加权调度矩阵
,
,
,
,
,
,
和
可获得如下:
图2绘制了每个节点接收状态的响应曲线。局部估计状态和融合估计状态如图3所示,这显示了提出的融合估计方法的重要性。时变概率参数由图4提供。
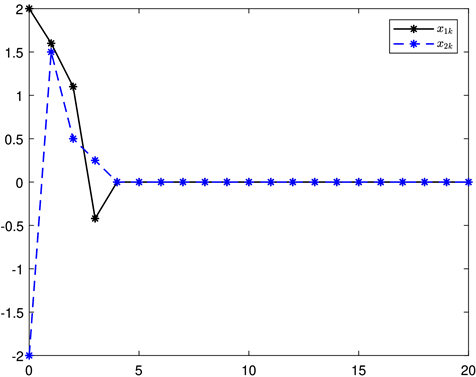
Figure 2. Response curve of each node receiving state
图2. 每个节点接收状态的响应曲线

Figure 3. Receiving state estimation and weighted fusion state estimation for each node
图3. 每个节点接收状态估计和加权融合状态估计
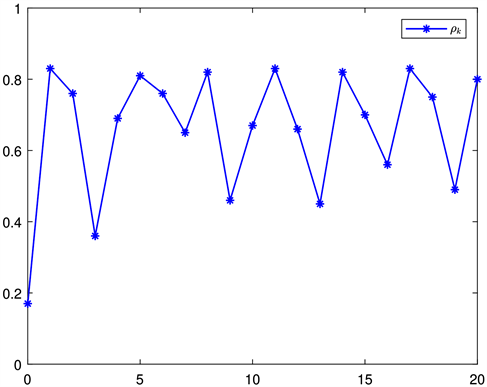
Figure 4. Time-varying probability parameter
图4. 时变的概率参数
5. 总结
本文研究了随机出现在传感器网络上的非线性问题的离散时间随机系统的概率依赖加权调度滤波问题。假定测量丢失现象是随机发生的,并且每个传感器的丢失概率已由遵循一定概率分布的单个随机变量管理,该概率分布在[0, 1]区间内 [9]。数值示例验证了上述设计程序的有效性。将来,我们还将考虑非线性随机系统的相关控制设计问题。