SARIMA模型在新疆布鲁氏菌病发病预测中的应用

Application of SARIMA Model in Prediction of Brucellosis in Xinjiang

摘要: 本文收集了2004年1月~2016年12月的新疆布病的月发病数，通过对数据进行序列平稳化、模型识别、模型检验的处理，预测了2017年12个月的布病发病数，拟合了2016年2月~12月的值，并与2016年2月~12月的实际值比较，最终建立了SARIMA(1,1,0)(0,1,0)12模型(AIC = 1606.44)，具有较高的有效性和合理性，该模型较好地拟合了新疆布病的新发病数，认为SARIMA模型可用于布病的短期预测和有效预防。

Abstract: In order to fit the new incidence of brucellosis in Xinjiang, this paper uses ARIMA(P,D,q)(P,D,Q)12 model to make short-term prediction and discusses the feasibility of the model. This paper collects the monthly incidence of human brucellosis in Xinjiang from January 2004 to December 2016, and uses R software to find the optimal model and make prediction. First, the incidence of brucellosis in the 12 months of 2017 is predicted. Secondly, the value from February to December 2016 is fitted, and compared with the actual value from February to December 2016, the ARIMA(1,1,0)(0,1,0)12 model (AIC = 1606.44) is finally established, which has higher effectiveness and rationality. The model fits the new incidence of human brucellosis in Xinjiang well, and can be used for short-term prediction and effective prevention of brucellosis.

1. 引言

在过去30多年中，平均2年就有一种新的能够影响人类健康的传染病出现，在这些新发传染病中有75%都是人畜共患病 [1]。布鲁氏菌病(简称布病)是由布鲁氏菌引起人和动物的一种共患性传染病，1905年在我国上海首次被发现 [2]，它是由布鲁氏菌属的小型革兰氏阴性球杆菌引起的慢性、人畜共患传染病，传染源主要是病畜，感染动物可长期带菌，成为对动物和人类最危险的传染源 [3]。

新疆属于农业部布病防控区域化管理的一类地区，人间布病疫情呈较高的发病态势 [4]。在新疆多数人偏爱以牛羊肉为食，由于布病影响食品安全问题，所以预测布病的发病率有重要的意义。一是可以根据布病预测数据，有针对性地开展防治工作，有助于提高布病预防控制工作的能力；二是在疫情监测工作中，根据预测数据的置信区间，可以判断实际发病率是否在正常范围波动。一般年份(或月份)，传染病的发病率按照既往的变化规律如线性趋势、季节性、周期性发生变动。如果实际发病率在预测值95%置信区间内波动，表明当月疫情基本正常，如果超出预测值95%置信区间，表明当月疫情已不同于以往流行规律，应警惕传染病暴发或流行的可能。因此，对传染病数据作预测是非常有必要的，常用的预测模型方法有时间序列法、灰色系统法、人工神经网络法等。

本文主要是用的时间序列法，例如有一些学者用了一些方法研究传染病的流行趋势，潘姣姣等人(2012)分别用曲线回归法、指数平滑法和ARIMA模型模拟肺结核疫情的动态轨迹，结果显示其中ARIMA模型有效拟合了类似肺结核发病率的动态趋势 [5]。陆波等人(2014)的研究，得出ABIMA模型能够有效预测流感 [6]。陈纯等人(2016)用R软件中的Holt-Winter指数匀滑模型和SARIMA有效地预测了广州市手足口病的发病情况，结果SARIMA为较佳的预测分析模型 [7]；易燕飞(2016)用了ARIMA时间序列模型和ARIMA乘积模型，预测了乙类传染病中的乙肝、结核病和丙类传染病中的流行性感冒的传染病流行趋势，结果显示ARIMA乘积模型的预测效果优于ARIMA模型 [8]。徐秦琴等人(2017)用SARIMA模型较好地拟合了淄博市流行性腮腺炎的动态变化 [9]。汪鹏等人(2018)比较ARIMA模型和Holt-Winters模型在武汉市流感样病例预测中的应用，结果ARIMA模型拟合效果较好，预测精度更高 [10]。

本文选用新疆布病发病数作为研究对象，主要用的时间序列的方法对新疆布病作拟合，并预测。其中步骤为原始序列平稳性检验、模型识别、参数估计及模型诊断与优化、模型预测。

2. 资料与方法

2.1. 数据来源

如图1所示，新疆维吾尔自治区统计局报道的2004年1月~2016年12月期间新疆人间布病的月发病数，可以看出每年发病数有上升的趋势，在6月份前后为高峰期。

2.2. 模型的建立

1) 季节效应分析

如图2所示，季节分解后，有上升的趋势性。有明显的季节性，并且以1年为周期，而且每年的布病高发季节和低发季节都很稳定。

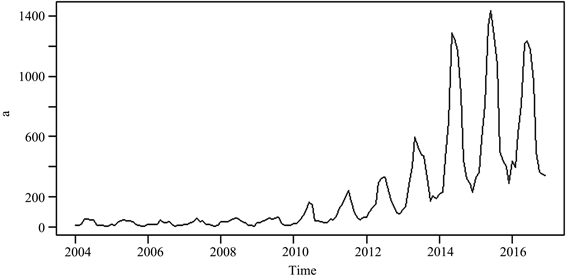
Figure 1. Monthly incidence of brucellosis in Xinjiang from January 2004 to December 2016 (a)

图1. 2004年1月~2016年12月新疆布鲁氏菌病月发病数(a)

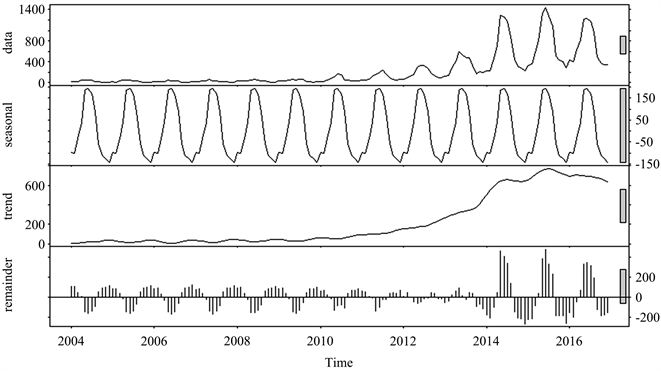
Figure 2. Decomposition of seasonal factors of brucellosis in Xinjiang

图2. 新疆布病季节因素分解

2) SARIMA模型介绍

SARIMA模型：较早的文献也称其为乘积ARIMA模型，是随机季节模型与ARIMA模型的结合，对于时间序列{Z, t = 1, 2, ∙∙∙}有季节性、趋势性和周期性时，可以建立非平稳季节模型，表示为SARIMA (p,d,q)(P,D,Q)的模型，其一般形式为 [11]：

${\varphi }_p\left(L\right){\Phi }_p\left(L^s\right){\left(1-L\right)}^d{\left(1-L^s\right)}^D{Z}_t={\theta }_q\left(L\right){\Theta }_Q\left(L^s\right){\epsilon }_t$

其中：

${\varphi }_p\left(L\right)=1-{\varphi }_{1}L-{\varphi }_2{L}^2-\cdots -{\varphi }_p{L}^p$

${\Phi }_P\left(L^s\right)=1-{\varphi }_s{L}^s-{\varphi }_{2s}{L}^{2s}-\cdots -{\varphi }_{Ps}{L}^{Ps}$

${\theta }_q\left(L\right)=1-{\theta }_{1}L-{\theta }_2{L}^2-\cdots -{\theta }_q{L}^q$

${\Theta }_Q\left(L^s\right)=1-{\Theta }_s{L}^s-{\Theta }_{2s}{L}^{2s}-\cdots -{\Theta }_{Qs}{L}^{Qs}$

p为非季节自回归阶数，P为季节自回归阶数，q为非季节移动平均阶数，Q为季节自回归阶数。 $d,D$ 分别为普通差分和季节差分的阶数，s 为季节的长度， ${\epsilon }_t$ 为白噪声序列。

3) SARIMA模型建立步骤

根据对研究序列的分析可确定和建立适当的模型：

a) 原始序列检验：ADF单位根检验，当P < 0.05时可认为序列平稳。

b) 非平稳序列平稳化：根据平稳序列acf图和偏自相关系数pacf图，选择适当的阶数。

c) SARIMA模型识别，模型识别过程中为了避免因经验不足而导致的模型识别不准确问题，使用Ｒ软件auto.arima函数自动识别模型阶数，并给出模型参数 [12]。

d) 参数估计及模型诊断与优化：运用最大似然估计，充分利用序列的信息对模型中未知参数进行估计。模型检验参数的显著性检验，当P < 0.05时可认为参数显著。通过模型检验的SARIMA(p,d,q)(P,D,Q)12模型，可采用赤则准则(AIC)，贝叶斯信息准则(BIC)确定最优模型。

e) 模型预测：选择最优模型，在80%和95%的置信区间进行短期预测。

预测过程包括选择方法或者模型来拟合数据，然后根据拟合的模型进行预测，预测的好坏，用预测精度来度量，该文用了两种误差，如下：

均方根误差

$\text{RMSE}=\sqrt{n^{-1}{\displaystyle \underset{t=1}{\overset{n}{\sum }}{\left(e_t\right)}^2}}$

平均绝对标准化误差

$\text{MASE}=n^{-1}{\displaystyle \underset{t=1}{\overset{n}{\sum }}\left|e_t\right|/q}$

(在MASE中，q对不同的对象有不同的意义，下面是针对季节性时间序列)

$q=\frac{1}{n-m}{\displaystyle \underset{t=m+1}{\overset{n}{\sum }}\left|x_t-x_{t-m}\right|}$

3. 结果

3.1. 原始序列平稳性检验

原始序列为非白噪声序列才有研究的意义。采用了Ljung-Box检验法，结果P < 0.05，所以该序列为非白噪声。用ADF单位根检验法，显示原序列为非平稳序列，所以先要非平稳序列平稳化。

如图3所示，分别将原序列一阶差分、一阶季节差分、一阶差分后再季节差分，结果显示一阶差分后再季节差分后的序列，经过ADF单位根检验，P = 0.01说明差分后序列平稳。

3.2. 模型识别

如图4所示，是一阶差分在一阶季节差分后平稳状态后的acf图和pacf图，所以可确定在SARIMA (p,d,q)(P,D,Q)12模型中d = 1，D = 1，看图可分析出p可能取值为0或1，q可能取值为1或2，P可能取值为0或1，Q可能取值为0或1，也可以用auto.arima函数，它可以实现ARIMA模型的初步定阶，识别为SARIMA(0,1,1)(0,1,0)12为当前模型 [13]。

Figure 3. Various difference graphs of the sequence of a: { $\nabla X_t$ } (top), { ${\nabla }_{12}{X}_t$ } (middle), { $\nabla {\nabla }_{12}{X}_t$ } (bottom)

图3. a序列的各种差分图：{ $\nabla X_t$ } (上)，{ ${\nabla }_{12}{X}_t$ } (中)，{ $\nabla {\nabla }_{12}{X}_t$ } (下)

Figure 4. acf and pacf graphs after first-order difference and second-order seasonal difference

图4. 一阶差分再一阶季节差分后的acf和pacf图

3.3. 参数估计及模型诊断与优化

3.3.1. 参数估计

SARIMA(p,d,q)(P,D,Q)12模型可能的组合结果如表1所示。首先考虑建立SARIMA(2,1,2)(1,1,1)12模型，若显著性水平α = 0.1，其中变量MA(1)的t值 = −0.3605、P = 0.3595 > 0.1，SAR(1)的t值 = 0.4837、P = 0.3147 > 0.1、SMA(1)的t值 = −0.5645、P = 0.2866 > 0.1，三者都没通过t检验。然后剔除变量MA(1)、SAR(1)、SMA(1)，尝试建立SARIMA(2,1,0)(0,1,0)12模型，变量AR(2)的t值 = 0.3238、P = 0.3733 > 0.1，所以剔除AR(2)，建立SARIMA(1,1,2)(0,1,0)12，变量AR(1)、MA(1)不显著，剔除AR(1)，建立SARIMA (0,1,2)(0,1,0)12，变量MA(2)不显著，所以剔除MA(2)，建立SARIMA(0,1,1)(0,1,0)12，t检验通过，在这提一下，R语言里的auto.arima函数可以帮助我们找到合适的模型，也就是它的参数检验都通过，刚好该函数选择的模型就是SARIMA(0,1,1)(0,1,0)12，接着建立SARIMA(1,1,0)(0,1,0) [12] 模型，t检验也通过。

Table 1. Parameter estimation and model diagnosis of SARIMA model

表1. SARIMA模型的参数估计和模型诊断

3.3.2. 模型诊断与优化

分别对SARIMA(0,1,1)(0,1,0)12模型和SARIMA(1,1,0)(0,1,0)12模型的残差进行白噪声检验，如图5、图6所示，白噪声检验主要采用了残差的密度直方图和密度估计、正态QQ图。这两个模型的直方图的残差密度有点对称，正态QQ图也类似正态分布，所以两个模型的残差都类似于白噪声。

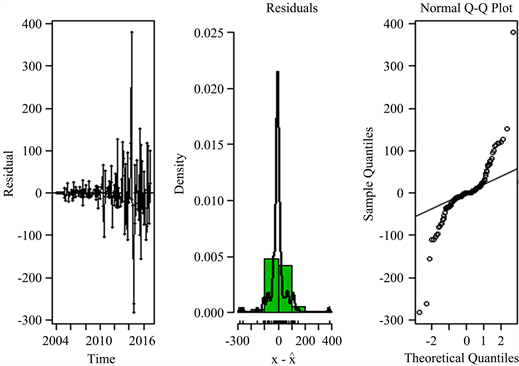
Figure 5. Residual sequence (left), density histogram and density estimation (middle), normal QQ graph (right) of SARIMA(0,1,1)(0,1,0)12 model

图5. SARIMA(0,1,1)(0,1,0)12模型的残差序列(左)、密度直方图和密度估计(中)、正态QQ图(右)

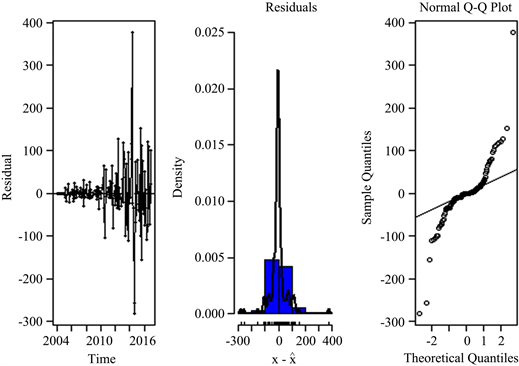
Figure 6. Residual sequence (left), density histogram and density estimation (middle), normal QQ graph (right) of SARIMA(1,1,0)(0,1,0)12 model

图6. SARIMA(1,1,0)(0,1,0)12模型的残差序列(左)、密度直方图和密度估计(中)、正态QQ图(右)

如表2所示，针对这两个模型可通过AIC和BIC的值越小原理RMSE和MASE的值最小选取最优模型，从而可将SARIMA(1,1,0)(0,1,0)12模型最初判定为最优模型AIC = 1606.44，BIC = 1612.362。模型参数的系数也都通过检验P < 0.1，最终SARIMA(1,1,0)(0,1,0)12模型被确认为最优模型。

Table 2. Selection criteria test of optimal SARIMA model

表2. 最优SARIMA模型的选取准则检验

3.4. 模型预测

1) 预测2017年1月~2017年12月的新发病数

如图7所示，采用SARIMA(1,1,0)(0,1,0)12模型，预测新疆人间布病2017年1月~2017年12月新发病数。如表3所示，2017年1月~2017年11月的预测值以及预测区间。

2) 2016年1月以前的数据作为训练集，2016年2月以后的数据作为测试集

如图8所示，采用SARIMA(1,1,0)(0,1,0)12模型，通过2004年1月~2016年1月的数据(训练集)拟合并预测新疆人间布病2016年2月~2016年12月新发病数(测试集)。如表4所示，2016年2月-2016年12月的预测值以及预测区间。如表5所示，训练集与测试集的模型交叉验证，可以看出该模型较为合理的拟合出新疆新发的人间布病数量。

Figure 7. The ARIMA(1,1,0)(0,1,0)12 model is proposed to predict the new incidence of human brucellosis in Xinjiang from January to December 2017

图7. SARIMA(1,1,0)(0,1,0)12模型拟合并预测新疆人间布病2017年1月-12月新发病数

Table 3. The ARIMA(1,1,0)(0,1,0)12 model with 80% and 95% confidence intervals predicts the number of new cases of human brucellosis in Xinjiang from January 2017 to November 2017

表3. 在置信区间80%和95%下的SARIMA(1,1,0)(0,1,0)12模型预测新疆人间布病2017年1月~2017年11月新发病数

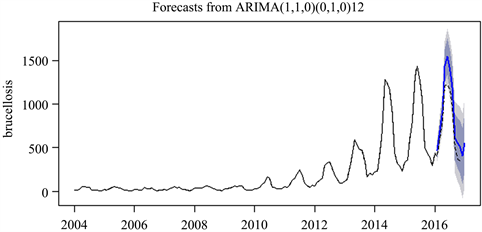
Figure 8. The ARIMA(1,1,0)(0,1,0)12 model is proposed to predict the new incidence of human brucellosis in Xinjiang from February to December 2016, and compare with the actual value from February to December 2016

图8. SARIMA(1,1,0)(0,1,0)12模型拟合并预测新疆人间布病2016年2月~12月新发病数，以及与2016年2月~12月实际值比较

Table 4. SARIMA(1,1,0)(0,1,0)12 model predicted and actual values under confidence intervals of 80% and 95%

表4. 在置信区间80%和95%下的SARIMA(1,1,0)(0,1,0)12模型预测值和实际值

Table 5. Model cross validation

表5. 模型交叉验证

4. 讨论

本文研究表明，在新疆布病研究中，SARIMA模型的建立过程可以分为四步：原始数据平稳化检验；模型识别；参数估计及模型诊断与优化；模型预测。我们使用SARIMA(p,d,q)(P,D,Q)12模型来分析新疆布病数据。最后用SARIMA(1,1,0)(0,1,0)12最优模型来预测布病新发病数。结果显示预测值与实际值都在80%置信区间和95%置信区间波动，这表明模型是合理的，且预测值是有效的。对SARIMA(1,1,0)(0,1,0)12模型的残差序列进行白噪声检验，判断该模型的合适性。其残差序列的检验值远大于判定值0.05，说明该模型的残差序列为白噪声序列，残差序列中有用的信息已被提取完，模型拟合程度很好。这证实了SARIMA模型的可行性。SARIMA模型考虑了时间序列的周期性和季度性变化，有较高的预测精度。但由于数据规模的限制，随着预测时间的延长，预测误差会逐渐增大，预测精度也会下降。为了比较SARIMA (0,1,1)(0,1,0)12模型和SARIMA(1,1,0)(0,1,0)12模型的预测精度，我们分析了两个模型的残差。因此，通过RMSE，MASE，AIC，BIC标准测试出最好的模型是SARIMA(1,1,0)(0,1,0)12模型。

利用SARIMA模型对疾病进行预测分析，有两大优点：1) 可以不考虑其他相关因素，只用考虑变量的自生变化；2) 可以用R语言的auto.arima函数自动定阶，出来个合适的模型，然后再去找最优模型。但是我们还应该注意：1) 至少需要50个以上的历史数据；2) 建立的模型只适合当前数据的短期预测，模型要随时更新。对于已建立的模型应不断加入新的实际值，以修正或重新拟合更优的模型 [14]。

学者们用不同模型来拟合一些传染病数据，并作预测，大部分为了比较这些方法的原理和实践中的差异。研究结果表明，尽管没有发现任何一种方法比其他方法更好，在未来的工作中，我们可以考虑其他模型应用于布病的研究，并寻求更精确的模型来预测新疆布病的发病率。

基金项目

新疆维吾尔自治区高校科研计划自然科学项目(XJEDU2021Y048)，新疆工程学院博士启动基金(2020xgy012302)共同资助。

NOTES

^*通讯作者。