零膨胀几何分布的变量选择

Variable Selection of Zero-Inflated Geometric Distribution

摘要: 在卫生服务和结果研究中，经常遇到计数结果，并且通常零占有有很大比例。零膨胀几何回归模型是分析几何部分过多零的有力工具。在实际建模中，搜集到的变量中可能存在与目标完全无关的变量(冗余变量)或者有些变量已知和目标相关，但实际的影响微乎其微。针对协变量多且具有相关性的问题，本文在似然函数的基础上添加SCAD、MCP和LASSO惩罚，得到基于零膨胀几何回归的惩罚目标函数，然后利用EM算法研究模型的参数估计和变量选择。仿真研究表明：该模型不仅具有准确的参数估计，而且比传统的逐步选择方法更优越。

Abstract: In health services and outcome research, count results are often encountered, and there is usually a large proportion of zeros. The zero-inflated geometric regression model is a powerful tool for analyzing excessive zeros in geometrical parts. In actual modeling, there may be variables that are completely unrelated to the target (redundant variables) among the collected variables, or some variables are known to be related to the target, but the actual impact is minimal. Aiming at the problem of many covariates and correlations, this paper adds SCAD, MCP and LASSO penalties to the likelihood function to obtain a penalty objective function based on zero-inflated geometric regression, and then uses the EM algorithm to study the parameter estimation and variable selection of the model problem. Simulation research shows that the model not only has accurate parameter estimation, but also is superior to the traditional stepwise selection method.

1. 引言

零膨胀模型广泛存在于各个领域：如社会科学、医学、工业、农业和生态学等。该类数据的特点是观测值中含有过多的零，若用传统的泊松(负二项或二项)回归模型对离散数据建模，拟合的结果就会出现较大偏差。因此，有很多学者开始了零膨胀模型的研究：早在1960年，Cohen Jr AC [1] 已经注意到零膨胀现象。直到1986年，Mullahy [2] 对常见的计数数据模型进行替代和测试，提出零膨胀模型。随着Lambert [3] (1992)的深入研究而广受欢迎。为了研究协变量的影响，他对零部分和非零部分分别建立logit连接模型和对数线性模型，提出了具有协变量因子的参数零膨胀泊松回归模型，并将其应用于印制电路板焊接缺陷的实例。随后，一个零膨胀(ZI)回归模型框架被提出并广泛应用于零过多问题。例如：Lee [4] [5] (2012a, b)在流行病学中应用ZI模型来研究男性乳头瘤病毒感染；Huang [6] 等(2017)提出了一种用于药物安全信号检测的ZI模型似然比检验；Liu和Powers [7] (2007)提出了一个应用于吸烟行为的ZI计数数据的生长曲线模型。而关于零膨胀几何分布的研究寥寥无几；肖翔 [8] (2018)开始零膨胀几何分布模型进行参数估计，2019年，提出零一膨胀几何回归模型 [9]，用来拟合数据中过多的零值和一值。因此，本文对零膨胀几何分布的研究很有意义。

变量选择对统计数据分析至关重要，识别重要的预测因子将提高拟合模型的预测性能。为了提高预测精度，选择有意义的变量，统计学家最初提出最优子集法来改进最小二乘估计，当设计矩阵正交时，最佳子集选择在传统的线性模型中的表现与最小二乘法一致。但是这个程序有两个基本限制：一是当预测数很多时，进行子集计算是不可行的；二是子集选择因其固有的离散性而变化极大(Breiman, 1996) [10]。逐步选择经常被用作子集选择的计算替代，然而它也遭受高可变性和经常陷入局部最优解而不是全局最优解的问题。此外，这些选择过程忽略了变量选择阶段的随机误差或不确定性。微小的数据变化就会导致不同的模型(Shen & Ye, 2002) [11]。为了能够自动简捷的选择变量，惩罚函数的思想开始流行，Hoerl和Kennard [12] (1970)提出岭回归，Frank和Friedman [13] (1993)将最小二乘估计、最优子集和岭回归整合到一个共同的框架中，分析其各自的适用性。Tibshirani [14] (1996)提出最小绝对收缩和选择算子(Lasso)，它是利用l₁惩罚通过连续收缩自动选择重要变量，从而保留了最佳子集选择和岭回归的良好特征。在惩罚回归算法中，低于某个阈值的系数被设置为零，否则将向零收缩。Nicolai Meinshausen [15] (2007)表明如果潜在的模型满足某些条件，则用Lasso选择变量是一致的。随着对惩罚函数的进一步探索，Fan和Li [16] (2001)研究了包括Lasso在内的一类惩罚函数，指出Lasso可以自动进行变量选择因为l₁惩罚在原点是奇异的，另一方面Lasso收缩程序产生了对大系数的有偏估计，因此就估计风险而言，它可能是次优的。Fan和Li [17] (2006)也指出一个好的惩罚函数应该具有oracle性(稀疏性、连续性和无偏性)，提出了平滑限幅绝对偏差(SCAD)惩罚。在2006年，他们对特征选择进行了全面的综述，并提出了一个统一的惩罚似然框架来处理变量选择问题。Zou [18] (2005)提出了弹性网惩罚，模拟表明当预测数远大于观测数时，该方法比Lasso有效。2006年，提出了用于同时估计和变量选择的自适应Lasso惩罚，添加自适应加权l₁惩罚满足惩罚函数的神谕性，很好地解决了多重共线性的问题。Zhang [19] (2010)提出的MCP惩罚。Buu [20] 等(2011)提出一步SCAD方法对ZI模型进行变量选择；Wang [21] 等(2014)对比了LASSO、SCAD和MCP三种惩罚函数。Chen [22] 等(2016)把SCAD惩罚应用到重复测量的零膨胀模型中。

2. 惩罚ZIGe回归模型

2.1. 惩罚ZIGe回归模型的变量选择

对每一个个体 $i=1,2,\cdots ,n$，定义其响应变量 $Y_i$ 之间是相互独立的。零膨胀几何分布是退化零分布和几何分布构成的混合分布，那么 $Y_i$ 的概率密度函数为：

$P\left(Y_i=y_i\right)=\{\begin{array}{l}{p}_i+\left(1-p_i\right)\left(1-{\theta }_i\right),y_i=0\hfill \\ \left(1-p_i\right)\left(1-{\theta }_i\right){\theta }_i{}^{y_i},y_i=1,2,\cdots \hfill \end{array}$ (1)

其中参数 $p_i\left(0\le p\le 1\right)$ 为容纳过多零的混合概率参数，参数 ${\theta }_i$ 表示几何分布中事件发生的概率。当 $p=0$ 时，ZIGe分布退化为标准的几何分布；当 $p>0$ 时，表明存在零膨胀。 $p$ 越大，说明数据中零的比例越大，非几何分布的数据所占的比例也就越大。在ZIGe回归模型中，混合概率 $p_i$ 和事件发生概率 ${\theta }_i$ 都是通过logistic回归模型建立连接关系：

$\{\begin{array}{c}logit\left(p_i\right)=W_i^{\text{T}}\gamma \\ logit\left({\theta }_i\right)=X_i^{\text{T}}\beta \end{array}$ (2)

其中 $W_i{}^{\text{T}}=\left(1,W_{i1},W_{i2},\cdots ,W_{iq}\right)$ 和 $X_i^{\text{T}}=\left(1,X_{i1},X_{i2},\cdots ,X_{ip}\right)$ 均是协变量随机变量； $\gamma ={\left({\gamma }_0,{\gamma }_1,{\gamma }_2,\cdots ,{\gamma }_q\right)}^T$ 和 $\beta ={\left({\beta }_0,{\beta }_1,{\beta }_2,\cdots ,{\beta }_p\right)}^{\text{T}}$ 均是可估的未知回归系数， ${\beta }_0$ 和 ${\gamma }_0$ 是截距项。假设 $\left\{\left(Y_i,X_i,W_i\right),i=1,2,\cdots ,n\right\}$ 独立观测的样本量， $\phi =\left(\beta ,\gamma \right)$ 是未知的 $p+q$ 维系数。观测样本的对数似然函数为：

$\begin{array}{c}\mathcal{l}\left(\phi ;y_i,x_i,w_i\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}\log \left\{I_{\left(y_i=0\right)}\left[\frac{p_i}{\left(1-p_i\right)}+\left(1-{\theta }_i\right)\right]\left(1-p_i\right)+I_{\left(y_i>0\right)}\left[{\theta }_i{}^{y_i}\left(1-{\theta }_i\right)\right]\left(1-p_i\right)\right\}}\\ ={\displaystyle \underset{i=1}{\overset{n}{\sum }}\log \left(\exp \left(W_i{}^{\text{T}}\gamma \right)+{\left(1+\exp \left(X_i{}^{\text{T}}\beta \right)\right)}^{-1}\right)-\log \left(1+\exp \left(W_i{}^{\text{T}}\gamma \right)\right)}\\ +{\displaystyle \underset{i=1}{\overset{n}{\sum }}{I}_{\left(y_i>0\right)}\left[y_i{X}_i{}^{\text{T}}\beta -\left(y_i+1\right){\left(1+\exp \left(X_i{}^{\text{T}}\beta \right)\right)}^{-1}\right]}\end{array}$ (3)

其中 $\theta$ 可直接最大化 $\mathcal{l}\left(\theta \right)$ 或者EM算法进行估计。值得注意的是，文章只考虑了logistic回归部分和几何分布回归部分具有相同协变量的情况，但是所提出的方法可以很容易地扩展到对于两个回归部分具有不同协变量的情况。

关于变量选择，考虑如下的惩罚零膨胀几何模型：

$p\mathcal{l}\left(\phi ;y_i,x_i,w_i\right)=\mathcal{l}\left(\phi ;y_i,x_i,w_i\right)-p\left(\beta ,\gamma \right)$ (4)

其中非负罚函数由下式给出：

$p\left(\beta ,\gamma \right)=n{\displaystyle {\sum }_{j=1}^{p_1}{p}_{a_j}\left|{\beta }_j\right|}-n{\displaystyle {\sum }_{k=1}^{p_2}{p}_{b_k}\left|{\gamma }_k\right|}$ (5)

其中 $p_{a_j}(\cdot )$ 和 $p_{b_k}(\cdot )$ 是惩罚函数， $a_j,b_k$ 是调节参数。回归系数 ${\beta }_j,{\gamma }_k$ 可以有不同的惩罚项。Fan [17] 所提出的SCAD惩罚定义如下：

$p_{\lambda }\left(\xi \right)=\{\begin{array}{l}\lambda \left|\xi \right|,\left|\xi \right|\le \lambda \hfill \\ \frac{\left(a^2-1\right){\lambda }^2-{\left(\left|\xi \right|-a\lambda \right)}^2}{2\left(a-1\right)},\lambda <\left|\xi \right|\le a\lambda \hfill \\ \frac{\left(a+1\right){\lambda }^2}{2},\left|\xi \right|>a\lambda \hfill \end{array}$ (6)

即当 $\left|\theta \right|$ 较小时，惩罚函数为线性函数；当 $\left|\theta \right|$ 较大时，为二次惩罚；而当 $\left|\theta \right|$ 很大时，惩罚项为常数。 $a,\lambda$ 均为调节参数， $\lambda$ 控制所选模型的复杂度，当 $n\to \infty$， $\lambda$ 趋于0。通常情况下，设置 $a=3.7$。SCAD惩罚函数关于 $\varphi$ 的一阶导函数为：

${p^{\prime }}_{\lambda }\left(\xi \right)=\{\begin{array}{l}\lambda ,\left|\xi \right|\le \lambda \hfill \\ \frac{a\lambda -\xi }{a-1},\lambda <\left|\xi \right|\le a\lambda \hfill \\ 0,\left|\xi \right|>a\lambda \hfill \end{array}=\lambda \left\{I\left(\xi \le \lambda \right)+\frac{{\left(a\lambda -\xi \right)}_{+}}{\left(a-1\right)\lambda }I\left(\xi >\lambda \right)\right\}$ (7)

Zhang [19] 提出的MCP惩罚函数定义如下：

$p_{\lambda ,\gamma }\left(a,c\right)={\displaystyle {\sum }_{i=1}^n\left(\rho \left(\left|a_i\right|;\lambda ,\gamma \right)+\rho \left(\left|c_i\right|;\lambda ,\gamma \right)\right),\lambda >0,\gamma >0}$ (8)

$\rho \left(\left|\xi \right|;\lambda ,\gamma \right)=\{\begin{array}{l}\lambda \left|\xi \right|-\frac{{\xi }^2}{2\gamma },\left|\xi \right|\le \lambda \gamma \hfill \\ \frac{1}{2}{\lambda }^2\gamma ,\left|\xi \right|>\lambda \gamma \hfill \end{array},\lambda \ge 0,\gamma >1,\xi =\left(a,c\right)$ (9)

其一阶导数为：

$\rho \left(\left|\xi \right|;\lambda ,\gamma \right)=\lambda {\left(1-\frac{\left|\xi \right|}{{\gamma }^{\lambda }}\right)}_{+}\mathrm{sgn}\left(\left|\xi \right|\right)$ (10)

Lasso惩罚定义如下：

$p\left(\lambda ;\left|\xi \right|\right)=\lambda \left|\xi \right|,\lambda \ge 0$ (11)

图1展示了 $a=3.7,\lambda =1$ 时的LASSO和SCAD函数及其导数图。左边是函数 $p_{\lambda }\left|\beta \right|$，右边是函数的一阶导数。非凸SCAD惩罚的吸引力在于：当 $\left|\beta \right|$ 增加时，它们不会过度惩罚导数为零的较大系数。

Fan和Li [16] (2001)中通过相应定理的直接应用，可以推出惩罚零膨胀几何回归模型的ORACLE性。因此，如果 ${\lambda }_{Ge,n}=0，{\lambda }_{BI,n}=0,\sqrt{n}{\lambda }_{Ge,n}\to \infty ,\sqrt{n}{\lambda }_{BI,n}\to \infty$，则ZIGe-MCP，ZIGe-SCAD具有神谕性：在概率趋于1时，无效应系数的估计量为0，有效应系数的估计量具有渐近正态分布，均值为非零系数的真值，方差为非零系数对应的费希尔信息矩阵的子矩阵。

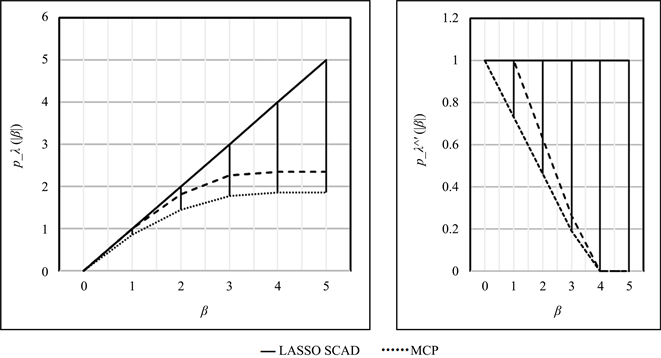
Figure 1. LASSO, MCP and SCAD penalties when λ = 1 and a = 3.7

图1. λ = 1, a = 3.7时的LASSO、MCP和SCAD惩罚

2.2. EM算法

根据Lambert (1992)的文章，零膨胀几何模型可以通过EM算法进行最大似然估计拟合。当 $Y_i$ 来自于零部分时，定义未观测到的随机变量 $B_i=1$。当 $Y_i$ 来自于二项部分时， $B_i=0$。因为 $B={\left(B_1,B_2,\cdots ,B_n\right)}^{\text{T}}$ 是不可观测的，它通常被视为缺失数据。EM算法就可以极好的处理缺失数据问题。如果完整数据 $\left(Y_i,B_i\right)$ 是可得到的，那么完整函数的对数似然函数为：

${\mathcal{l}}^c\left(\phi ;y_i,z_i\right)={\displaystyle {\sum }_{i=1}^n\left\{B_i{W}_i{}^{\text{T}}\gamma -\log \left(1+{\text{e}}^{W_i{}^{\text{T}}\gamma }\right)+\left(1-B_i\right)\left[y_i{X}_i^{\text{T}}\beta -\left(y_i+1\right)\log \left(1+{\text{e}}^{X_i^{\text{T}}\beta }\right)\right]\right\}}$ (12)

则惩罚完全数据的对数似然函数为：

$\begin{array}{l}p{\mathcal{l}}^c\left(\phi ;y_i,z_i\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left\{B_i{W}_i^{\text{T}}\gamma -\log \left(1+\exp \left(W_i{}^{\text{T}}\gamma \right)\right)\right\}}-n{\displaystyle \underset{k=1}{\overset{p_1}{\sum }}{p}_{a_j}\left|{\beta }_j\right|}\\ +{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(1-B_i\right)\left[y_i{X}_i^{\text{T}}\beta -\left(y_i+1\right)\log \left(1+{\text{e}}^{X_i^{\text{T}}\beta }\right)\right]}-n{\displaystyle \underset{k=1}{\overset{p_2}{\sum }}{p}_{b_k}\left|{\gamma }_k\right|}\end{array}$ (13)

因此，惩罚对数似然函数可看作是关于 $B_i$ 的线性函数， $p{\mathcal{l}}^c\left(\gamma ;y_i,z_i\right)$ 和 $p{\mathcal{l}}^c\left(\beta ;y_i,z_i\right)$ 分别用logistic回归和加权几何回归求得最大值。利用EM算法：E步通过给定观测数据和先前参数估计 ${\phi }^{(m)}$ 来计算条件期望 $\delta$ 的条件期望；M步求使 ${\mathcal{l}}^c\left(\phi ;y_i,z_i\right)$ 极大化的 $\phi$，确定第i + 1次迭代的参数估计值 ${\phi }^{(i+1)}=\left({\beta }^{i+1},{\gamma }^{i+1}\right)$。当 $\phi$ 收敛时，迭代停止。从初始值 ${\phi }^{(0)}=\left({\beta }^{(0)},{\gamma }^{(0)}\right)$ 开始，EM算法在以下三个步骤中迭代进行，直到收敛：

1) E步：给定观测数据并假设当前的估计 ${\phi }^{(m)}$ 提供模型的真实参数，迭代m次时 $\delta$ 的条件期望由下式给出：

${\hat{B}}_i{}^{(m)}=\{\begin{array}{l}{\left(\left(1+\exp {\left(W_i^{\text{T}}{\hat{\gamma }}^{\left(m\right)}\right)}^{-1}\right){\left(1+\exp \left(X_i^{\text{T}}{\hat{\beta }}^{\left(m\right)}\right)\right)}^{-1}\right)}^{-1},y_i=0\hfill \\ 0,y_i>0\hfill \end{array}$ (14)

因此，可以计算完整数据对数似然的期望值：

$\mathcal{Q}\left(\phi |{\hat{\phi }}^{\left(m\right)}\right)=E\left(p{\mathcal{l}}^c\left(\phi ;y_i,z_i\right)|y_i,{\hat{\phi }}^{\left(m\right)}\right)={\mathcal{Q}}_1\left(\gamma |{\hat{\phi }}^{\left(m\right)}\right)+{\mathcal{Q}}_2\left(\beta |{\hat{\phi }}^{\left(m\right)}\right)$ (15)

其中：

${\mathcal{Q}}_1\left(\gamma |{\hat{\phi }}^{\left(m\right)}\right)={\displaystyle {\sum }_{i=1}^n{\hat{B}}_i{}^{(m)}{W}_i^{\text{T}}\gamma }-\log \left(1+\exp \left(W_i^{\text{T}}\gamma \right)\right)-n{\displaystyle {\sum }_{k=1}^{p_1}{p}_{a_j}\left|{\beta }_j\right|}$ (16)

${\mathcal{Q}}_2\left(\beta |{\hat{\phi }}^{\left(m\right)}\right)={\displaystyle {\sum }_{i=1}^n\left(1-{\hat{B}}_i{}^{(m)}\right)}\left[y_i{X}_i^{\text{T}}\beta -\left(y_i+1\right)\log \left(1+e^{X_i^{\text{T}}\beta }\right)\right]-n{\displaystyle {\sum }_{k=1}^{p_2}{p}_{b_k}\left|{\gamma }_k\right|}$ (17)

2) M步(关于 $\gamma$ )：

${\hat{\gamma }}^{\left(m+1\right)}=\arg \underset{\gamma }{\underset{︸}{\max }}\mathcal{Q}\left(\gamma |{\hat{\gamma }}^{\left(m\right)}\right)$ (18)

3) M步(关于 β )

${\hat{\beta }}^{\left(m+1\right)}=\arg \underset{\beta }{\underset{︸}{\max }}\mathcal{Q}\left(\beta |{\hat{\beta }}^{\left(m\right)}\right)$ (19)

${\mathcal{Q}}_1\left(\gamma |{\theta }^{\left(k\right)}\right)$ 是一个加权惩罚逻辑对数似然函数， ${\mathcal{Q}}_2\left(\beta |{\theta }^{\left(k\right)}\right)$ 是一个惩罚逻辑回归对数似然函数，重复E步和M步直到收敛。

2.3. 调整参数的选择

惩罚参数 $\left(a_j,b_k\right)$ 由BIC准则选取：

$BIC=-2\mathcal{l}\left(\hat{\phi };a_j,b_k\right)+\log \left(n\right)df$ (20)

其中 $\hat{\phi }$ 是估计参数； $\left(a_j,b_k\right)$ 是调整参数； $\mathcal{l}(\cdot )$ 是对数似然函数； $df={\displaystyle {\sum }_{j=0}^{q1}I\left({\beta }_j\ne 0\right)}+{\displaystyle {\sum }_{k=0}^{q2}I\left({\gamma }_k\ne 0\right)}$ 是自由度。首先基于成对的收缩参数构造一个解路径，算法生成两个递减序列： $a_j{}^{(1)}>a_j{}^{(2)}>\cdots >a_j{}^{(M)}$ 和 $b_k{}^{(1)}>b_k{}^{(2)}>\cdots >b_k{}^{(M)}$。然后对序列进行配对： $\left(a_j{}^{\left(1\right)},b_k{}^{\left(1\right)}\right),\cdots ,\left(a_j{}^{\left(M\right)},b_k{}^{(M)}\right)$。原则上选择大的值 $\left(a_j{}^{\left(1\right)},b_k{}^{\left(1\right)}\right)$ 使得除了截距项外的所有系数都趋于零；而一种改进的方法表明最小值 $\left(a_j{}^{\left(1\right)},b_k{}^{\left(1\right)}\right)$ 可从LASSO惩罚的数据中计算得到。关于SCAD惩罚和MCP惩罚，本文也遵循这种策略。

3. 仿真模拟

3.1. 模型和数据生成

$\{\begin{array}{c}logit\left({\theta }_i\right)={\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+\cdots +{\beta }_{20}{x}_{i20}\\ logit\left(p_i\right)={\gamma }_1{w}_{i1}+{\gamma }_2{w}_{i2}+\cdots +{\gamma }_{20}{w}_{i20}\end{array}$

本文采用了Anne Buu提出的数据生成方案，在仿真研究中，协变量取自多元正态分布 $N_{20}\left(0,\text{Σ}\right)$，协方差阵 包含元素 ${\rho }^{\left|i-j\right|}\left(i,j=1,\cdots ,20\right)$。协变量之间的相关性 $\rho$ 分别设置为0.4和0.8；样本量n = 100, 300。计数部分和退化零部分的协变量相同，选择这些参数是为了获得不同数量的协变量和不同比例的零膨胀率。

模拟1：设置参数使得响应变量Y的零膨胀率为29%， $\rho =0.4$，样本量n分别为100和300，重复100次实验；模型中的真实参数向量为：

$\beta =\left(1.5,0,0,0,-0.22,0,0,0,-0.25,0,0.20,0,0.30,-0.32,0,0,0,0.20,0,0,0\right)$

$\gamma =\left(-1.05,0,0.45,0,-0.3,0,0,0,0,0,-0.33,0,-0.39,0,0,0.3,0,0,0,0.36,0\right)$

模拟2：设置参数使得响应变量Y的零膨胀率为29%， $\rho =0.8$，样本量n分别为100和300，重复100次实验；模型中的真实参数向量为：

$\beta =\left(1.5,0,0,0,-0.22,0,0,0,-0.25,0,0.20,0,0.30,-0.32,0,0,0,0.20,0,0,0\right)$

$\gamma =\left(-1.05,0,0.45,0,-0.3,0,0,0,0,0,-0.33,0,-0.39,0,0,0.3,0,0,0,0.36,0\right)$

模拟3：设置参数使得响应变量Y的零膨胀率为55%， $\rho =0.4$，样本量n分别为100和300，重复100次实验；模型中的真实参数向量为：

$\beta =\left(1.10,0,0,0,-0.36,0,0,0,0,0,0,0,0,-0.32,0,0,0,0,0,0,0\right)$

$\gamma =\left(0.3,-0.48,0,0,0,0.4,0,0,0,0,0.44,0,0.44,0,0,0,0,0,0,0,0\right)$

模拟4：设置参数使得响应变量Y的零膨胀率为55%， $\rho =0.8$，样本量n分别为100和300，重复100次实验；模型中的真实参数向量为：

$\beta =\left(1.10,0,0,0,-0.36,0,0,0,0,0,0,0,0,-0.32,0,0,0,0,0,0,0\right)$

$\gamma =\left(0.3,-0.48,0,0,0,0.4,0,0,0,0,0.44,0,0.44,0,0,0,0,0,0,0,0\right)$

3.2. 仿真结果

所选择的统计评估方法有惩罚ZIGe回归，显著水平分别为0.01，0.05和0.1573的逐步后退法以及假设非零系数已知的惩罚ZIGe回归模型。 $BE\left(\alpha \right)$ 是从全ZIGe模型中去除不重要的变量(包括Ge和零分量中的所有预测变量)，然后用剩余的预测因子重新调整模型，重复该过程，直到所有变量都基于 $\alpha$ 水平显著。估计的精度度通过所选择的模型和全ZIGe模型之间的参数均方误差比来衡量。为了评估变量选择的性能，我们计算了灵敏度(正确识别的非零系数数量的比例)和特异性(正确识别的零系数数量的比例)。为了比较预测精度，我们从每个模型中生成了与训练数据相同数量的测试观测值，并使用从训练数据中估计的参数来计算对数似然值并用箱线图来表示。参数估计和变量选择的结果总结在表1和表2以及附录(附表1和附表2)里面。

通过表1、表2、附表1、附表2的模拟结果得到：

1) 在零膨胀几何模型中，无论是零部分还是几何部分，LASSO在均方误差和特异性上都比SCAD和MCP表现更好，在敏感性上相反，ZIGe-MCP和ZIGe-SCAD方法之间没有明显的差别。BE方法的结果因显著性水平而异：在显著性水平较小时( $\alpha =0.01$ )，用较小的均方误差产生了更精确的估计，但可能选择较少的变量，导致不太精确的灵敏度；在显著性水平较大时( $\alpha =0.1573$ )，BE方法保留了更多的预测变量并且提高了灵敏度。就均方误差而言，BE (0.01)与ZIGe-MCP和ZIGe-SCAD相比具有竞争力。然而在所有的模拟情况中，BE (0.01)在零部分的敏感度最小，在小样本情况下尤其明显。

2) 随着样本量的增加，所有方法都有较好的性能(均方误差值降低)，零分量的灵敏度随之增加。表中的均方误差被定义为一个比率，而不是绝对值。当相关性增加时，我们在表1和附表1或者表2和附表2的结果中并未表明敏感性有明显变化。

3) 图2和图3展示了预测的对数似然值。惩罚的零膨胀几何模型比BE方法的预测效果要稍好点。在模拟1中，样本量为100时，LASSO惩罚的表现力相对来说最好的，SCAD没有优势，BE方法随着显著性水平的增加，预测效果逐渐变差；而当样本量增加为300时，几种惩罚方法的效果都有所提高。在模拟4中， $\rho$ 值变为0.8，零膨胀率由原来的29%变为55%，模型具有较好的预测能力。

Table 1. Results of simulation 1 (ρ = 0.4)

表1. 模拟1 (ρ = 0.4)的结果

Table 2. Results of simulation 4 (ρ = 0.8)

表2. 模拟4 (ρ = 0.8)的结果

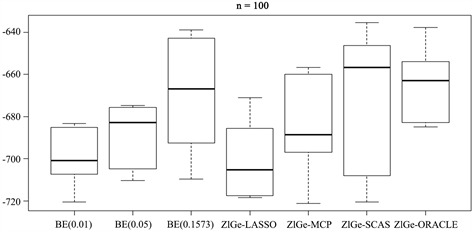
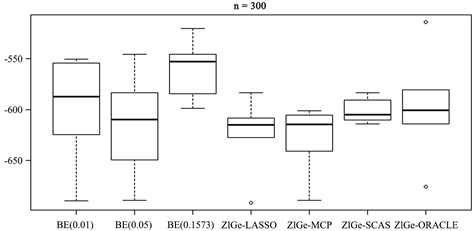
Figure 2. The log-likelihood value of simulation 1

图2. 模拟1的对数似然值

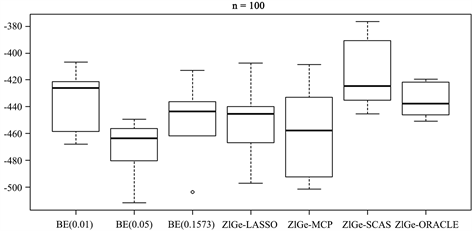
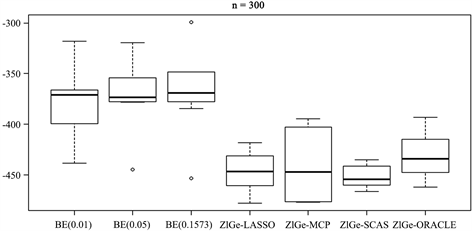
Figure 3. The log-likelihood value of simulation 4

图3. 模拟4的对数似然值

4. 讨论

预测因子的数量很大，而样本量却是小样本或者中等样本时，混合模型的变量选择是一个具有挑战性的问题，本文研究了ZIGe模型中变量选择的EM的性能。在实际建模中发现，数据中的协变量多且具有相关性，有的协变量对模型建立的效果影响微乎其微，有的协变量之间存在多重共线性。针对此问题，在最大似然函数的基础上添加SCAD、MCP和LASSO惩罚，得到基于零膨胀几何回归的惩罚目标函数，然后利用EM算法研究模型的参数估计和变量选择问题。仿真结果表明：该模型不仅具有准确的参数估计，而且比传统的逐步选择方法更优越。

在今后的研究中，可考虑如下四个方向的发展：

一是零膨胀几何模型推广。本文只考虑了零膨胀模型，若数据相关，可以推广到随机效应零膨胀几何回归模型或者半参数零膨胀模型中；若数据中零值和一值都很多，可推广到零一膨胀几何回归模型中。

二是惩罚函数的选择，本文考虑了常见的三种惩罚函数，后续可以尝试弹性网惩罚，自适应弹性网惩罚、贝叶斯惩罚等技术。

三是参数估计的求解方法，本文选择EM算法，另一种算法是采用对数似然函数的泰勒近似。但是，这种方法需要反演Hessian矩阵，相对比较复杂，但值得尝试。

四是未找到合适的数据进行实例分析，希望在下一步的研究中可以找到适合的数据，将理论运用到实际中，证实理论的正确性。

致谢

衷心地感谢我的研究生导师赵丽华老师，在整个学习及论文写作过程中，认真的指导；在生活中，经常告诫我不要有太大压力，做好自己，让我在漫漫学涯中感受到了温暖和肯定。其次，感谢给予转载和引用权的文献及研究思想和设想的所有者们，正是借助你们的肩膀，我才能够更好地完成论文的撰写。

附录

Table A1. Results of simulation 2 (ρ = 0.8)

附表1. 模拟2 (ρ = 0.8)的结果

Table A2. Results of simulation 3 (ρ = 0.4)

附表2. 模拟3 (ρ = 0.4)的结果