体积元几何与Jacobi行列式之关系

The Relationship between Volume Element Geometry Related and Jacobi Determinant

摘要: 在数学分析的学习中我们已经学习了弧长、面积、体积的求解方法，那这些方法是怎样得到的，是我们学习过程中需要探讨的一个非常重要的问题。为了方便我们在学习过程中对这一部分内容的理解、掌握，本文将从坐标变换、向量外积、向量内积三个不同的方面来介绍体积元与Jacobi行列的关系。

Abstract: In the study of mathematical analysis, we have learned the solving methods of arc length, area and volume, and how to use these methods to find physical quantities such as the mass of an object and the moment of inertia, which is a very important part in our learning process. In order to ensure that we have a better understanding of the content in the learning process, this thesis will introduce the relationship between volume elements and Jacobi rows from three different aspects of coordinate transformation, vector exterior product and vector inner product.

1. 引言

数学分析是数学及其它专业中一门基础课程，也是非常重要的一门学科，其内容也广泛地应用到生活的各个领域，例如在求解一些不规则物体的体积、质量、转动惯量等物理量时，我们就可以用到“分割、近似求和、取极限”这种方法，通过在求解的过程中选取一个合适的坐标系使积分区间变简单，或者被积的函数从而使积分的求解变得简单，以达到计算时事半功倍的效果，让求解过程变得容易，那么如何选取一个合适的坐标系对我们来是非常重要。

现有的各种数学分析教材基本上都是从一个方面来描述体积元几何与Jacobi行列式的关系，无法使我们通过对比更好地对这部分内容理解，为解决这一问题，本文将从坐标变换、向量外积、向量内积三个不同的方面对这部分内容进行叙述。

文中第一部分介绍的是标准《数学分析》 [1] 教材中关于弧长微元、面积微元、体积微元的处理，通过对书本上的内容进行归纳、整理使内容更加有条理性，有利于读者对内容的掌握，而且文中关于二重积分的变量变换与面积微元的内容是根据耿堤、易法槐 [2] 《数学分析(三)》来阐述，这本书利用我们比较熟悉的解析几何和Taylor公式的知识对定理进行证明，更有利于我们的理解。

第二部分内容参考欧阳光中、姚允龙 [3] 《数学分析》下册内容，利用我们从解析几何中已知的知识，首先介绍了外积的定义和性质，为我们对即将学习的内容做准备，然后对外积所表示的几何意义进行阐述，采用直观的描述方法将外积应用到积分变换中，从而得出体积元几何与Jacobi行列式的关系。由于这部分内容的直观性，积分的变量代换并未采取证明。

第三部分根据吕林根、许子道 [4] 《解析几何》中关于向量内积、外积定义，利用三角函数公式将它们联系起来，推出度量矩阵，然后通过向量内积和矩阵得出积分变换下体积元几何与Jacobi行列式新的表示形式。另外这部分内容关于面积微元的变换，利用外积和内积相结合的形式，更有利于我们的理解。

2. 弧长、面积、体积元的表示与Jacobi行列式

为了能让读者更快的进入到这篇论文的内容，本节以标准《数学分析》教材为准对弧长微元、面积微元、体积微元相关内容进行讲解，具体的一些知识可参考教材 [1] [2] [5]。

2.1. 平面曲线的弧长

定义2.1.1 设曲线C是一条没有自交点的非闭的平面曲线，由参数方程

$x=x\left(t\right),y=y\left(t\right),t\in \left[\alpha ,\beta \right]$ (1)

给出若 $x\left(t\right)$， $y\left(t\right)$ 在 $\left[\alpha ,\beta \right]$ 上连续可微，则C是可求弧长的。

定义2.1.2 设曲线C由参数方程(1)给出的。若 $x\left(t\right)$， $y\left(t\right)$ 在 $\left[\alpha ,\beta \right]$ 上连续可微，且 $x^{\prime }\left(t\right)$ 和 $y^{\prime }\left(t\right)$ 不同时为零(即 ${x^{\prime }}^2\left(t\right)+{y^{\prime }}^2\left(t\right)\ne 0$， $t\in \left[\alpha ,\beta \right]$ )，则称C是一条光滑曲线。

定义2.1.3 设光滑曲线C由参数方程(1)给出。见图1，PR为曲线在点P处的切线，在三角形PQR中，PQ为 $\text{d}x$，QR为 $\text{d}y$，PR则称为弧微分，记为 $\text{d}s$。见图1中三角形PQR称为微分三角形。

Figure 1. Differential triangle

图1. 微分三角形

在直角三角形中PQR由勾股定理得： $\text{d}s=\text{d}{x}^2+\text{d}{y}^2$，又 $\text{d}x=x^{\prime }\left(t\right)\text{d}t$， $\text{d}y=y^{\prime }\left(t\right)\text{d}t$，所以有弧微分

$\text{d}s=\sqrt{\text{d}{x}^2+\text{d}{y}^2}=\sqrt{{x^{\prime }}^2\left(t\right)+{y^{\prime }}^2\left(t\right)}\text{d}t$ (2)

推论1 设曲线C由极坐标方程

$r=r\left(\theta \right),\theta \in \left[\alpha ,\beta \right]$ (3)

表示，把它化为参数方程为

$x=r\left(\theta \right)\cos \theta ,y=r\left(\theta \right)\sin \theta ,\theta \in \left[\alpha ,\beta \right]$

由于

$x^{\prime }\left(\theta \right)=r^{\prime }\left(\theta \right)\cos \theta -r\left(\theta \right)\sin \theta ,$

$y^{\prime }\left(\theta \right)=r^{\prime }\left(\theta \right)\sin \theta +r\left(\theta \right)\cos \theta ,$

${x^{\prime }}^2\left(\theta \right)+{y^{\prime }}^2\left(\theta \right)=r^2\left(\theta \right)+{r^{\prime }}^2\left(\theta \right),$

由(2)可知

$\text{d}s=\sqrt{r^2\left(\theta \right)+{r^{\prime }}^2\left(\theta \right)}\text{d}\theta .$

推论2 设曲线C由直角坐标方程

$y=f\left(x\right),x\in \left[a,b\right]$ (4)

给出，把它化为参数方程为

$x=x,y=f\left(x\right),x\in \left[a,b\right].$

由(2)可知

$\text{d}s=\sqrt{1+{f^{\prime }}^2\left(x\right)}\text{d}x.$

定理1 设曲线C由参数方程(1)给出，若C是一条光滑曲线，则C是可求取弧长的，且弧长为

$s={\displaystyle {\int }_{\alpha }^{\beta }\sqrt{{x^{\prime }}^2\left(t\right)+{y^{\prime }}^2\left(t\right)}\text{d}t}.$

推论1 若曲线C由极坐标方程(3)给出，当 $r^{\prime }\left(\theta \right)$ 在 $\left[\alpha ,\beta \right]$ 上连续，且 $r\left(\theta \right)$ 和 $r^{\prime }\left(\theta \right)$ 不同时为零，此极坐标曲线为一条光滑曲线，此时弧长为

$s={\displaystyle {\int }_{\alpha }^{\beta }\sqrt{r^2\left(\theta \right)+{r^{\prime }}^2\left(\theta \right)}\text{d}\theta }.$

推论2 若曲线C由直角坐标方程(4)表示，当 $f\left(x\right)$ 在 $\left[a,b\right]$ 上连续可微时，此曲线是一条光滑曲线，此时弧长为

$s={\displaystyle {\int }_{\alpha }^{\beta }\sqrt{1+{f^{\prime }}^2\left(x\right)}\text{d}x}.$

2.2. 第一型曲线积分

定理2 设光滑曲线

$L:\{\begin{array}{c}x=\phi \left(t\right),\\ y=\psi \left(t\right),\end{array}t\in \left[\alpha ,\beta \right],$

函数 $f\left(x,y\right)$ 为定义在L上的连续函数，则

${\displaystyle {\int }_{L}f\left(x,y\right)\text{d}s}={\displaystyle {\int }_{\alpha }^{\beta }f\left(\phi \left(t\right),\psi \left(t\right)\right)}\sqrt{{{\phi }^{\prime }}^2\left(t\right)+{{\psi }^{\prime }}^2\left(t\right)}\text{d}t.$ (5)

推论1 当曲线L由方程

$y=\psi \left(x\right),x\in \left[a,b\right]$

表示，且 $\psi \left(x\right)$ 在 $\left[a,b\right]$ 上有连续的导函数时，(5)式成为

${\displaystyle \underset{L}{\int }f\left(x,y\right)\text{d}s}={\displaystyle {\int }_a^{b}f\left(x,\psi \left(x\right)\right)}\sqrt{{{\phi }^{\prime }}^2\left(x\right)+{{\psi }^{\prime }}^2\left(x\right)}\text{d}x.$

推论2 当空间曲线L是一条光滑的曲线，由参数方程 $x=\phi \left(t\right)$， $y=\psi \left(t\right)$， $z=\chi \left(t\right)$， $t\in \left[\alpha ,\beta \right]$ 表示时， $f\left(x,y,z\right)$ 是L上的连续函数，则弧微分为

$\text{d}s=\sqrt{{{\phi }^{\prime }}^2\left(t\right)+{\psi }^2\left(t\right)+{{\chi }^{\prime }}^2\left(t\right)}\text{d}t$

其弧长为

${\displaystyle \underset{L}{\int }f\left(x,y,z\right)\text{d}s}={\displaystyle {\int }_{\alpha }^{\beta }f\left(\phi \left(t\right),\psi \left(t\right),\chi \left(t\right)\right)}\sqrt{{{\phi }^{\prime }}^2\left(t\right)+{{\psi }^{\prime }}^2\left(t\right)+{{\chi }^{\prime }}^2\left(t\right)}\text{d}t.$

2.3. 二重积分的变量变换与面积微元

引理 设变换 $T\text{:}x=x\left(u,v\right)$， $y=y\left(u,v\right)$ 将 $uv$ 平面上按段光滑的封闭的曲线所围成的闭区域 $\text{Δ}$ 一对一的映射成 $xy$ 平面上的闭区域D，函数 $x\left(u,v\right)$， $y\left(u,v\right)$ 在 $\text{Δ}$ 内分别具有一阶连续偏导数且它们的函数行列式

$J\left(u,v\right)=\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)}\ne 0,\left(u,v\right)\in \text{Δ,}$

则 $\text{Δ}$ 和 $xy$ 平面上的对应区域D之间的微元面积伸缩系数为 $\left|J\left(u,v\right)\right|$，即

$\text{d}x\text{d}y=\left|J\left(u,v\right)\right|\text{d}u\text{d}v.$

证明 在 $\text{Δ}$ 上任取一个点 $A\left(u,v\right)$，以A为其中一个定点作一个矩形ABCD。它的4个顶点坐标分别为 $A\left(u,v\right)$， $B\left(u+\text{d}u,v\right)$， $C\left(u+\text{d}u,v+\text{d}v\right)$， $D\left(u,v+\text{d}v\right)$。在变换 $x=x\left(u,v\right)$， $y=y\left(u,v\right)$ 下， $\text{Δ}$ 上矩形ABCD相应的会得到 $xy$ 平面上一个曲边四边形，那 $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ 么它的四个顶点分别为 $A^{\prime }\left(x_1,y_1\right)$， $B^{\prime }\left(x_2,y_2\right)$， $C^{\prime }\left(x_3,y_3\right)$， $D^{\prime }\left(x_4,y_4\right)$ (见图2)。

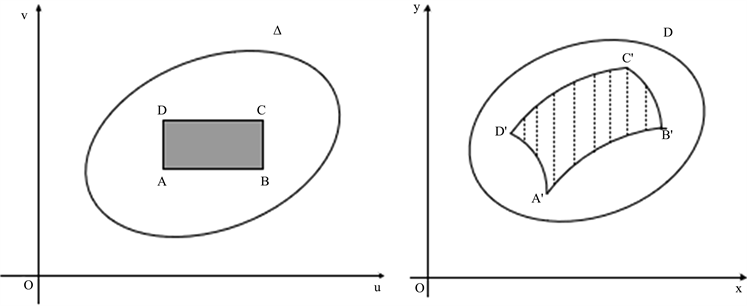
Figure 2. Area micro-element transformation

图2. 面积微元的变换

我们可以利用Taylor公式得到

$A^{\prime }:x_1=x\left(u,v\right),y_1=y\left(u,v\right);$

$\begin{array}{l}{B}^{\prime }:x_2=x\left(u+\text{d}u,v\right)=x\left(u,v\right)+\frac{\partial x\left(u,v\right)}{\partial u}\text{d}u+o\left(\text{d}u\right),\\ y_2=y\left(u+\text{d}u,v\right)=y\left(u,v\right)+\frac{\partial y\left(u,v\right)}{\partial u}\text{d}u+o\left(\text{d}u\right);\end{array}$

$\begin{array}{l}{C}^{\prime }:x_3=x\left(u+\text{d}u,v+\text{d}v\right)=x\left(u,v\right)+\frac{\partial x\left(u,v\right)}{\partial u}\text{d}u+\frac{\partial x\left(u,v\right)}{\partial v}\text{d}v+o\left(\text{d}u\right)+o\left(\text{d}v\right),\\ y_3=y\left(u+\text{d}u,v+\text{d}v\right)=y\left(u,v\right)+\frac{\partial y\left(u,v\right)}{\partial u}\text{d}u+\frac{\partial y\left(u,v\right)}{\partial v}\text{d}v+o\left(\text{d}u\right)+o\left(\text{d}v\right);\end{array}$

$\begin{array}{l}{D}^{\prime }:x_4=x\left(u,v+\text{d}v\right)=x\left(u,v\right)+\frac{\partial x\left(u,v\right)}{\partial v}\text{d}v+o\left(\text{d}v\right),\\ y_4=y\left(u,v+\text{d}v\right)=y\left(u,v\right)+\frac{\partial y\left(u,v\right)}{\partial v}\text{d}v+o\left(\text{d}v\right);\end{array}$

若想计算矩形 $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ 的面积，可将 $A^{\prime }{B}^{\prime }$， $B^{\prime }{C}^{\prime }$， $C^{\prime }{D}^{\prime }$， $D^{\prime }{A}^{\prime }$ 用直线连接起来作成一个四边形 $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$。当我们所取的 $\text{d}x$ 和 $\text{d}y$ 足够小时，在计算时就可以忽略髙阶无穷小量，此时曲边四边形的面积就可以等于四边形 $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ 的面积。

由 $x_i,y_i\left(i=1,2,3,4\right)$ 的表达式，当计算假设是省略掉 $o\left(\text{d}u\right)$ 和 $o\left(\text{d}v\right)$，则

$x_2-x_1=x_3-x_4,x_4-x_1=x_3-x_2,$

$y_2-y_1=y_3-y_4,y_4-y_1=y_3-y_2$.

所以在四边形 $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ 中，两两对边的距离是相等的，所以当忽略高阶无穷小量时，曲边四边形相当于—个平行四边形(见图3)。

Figure 3. Curved quadrilateral

图3. 曲边四边形

它的面积 $\text{d}\Sigma$ 是三角形 $A^{\prime }{B}^{\prime }{C}^{\prime }$ 面积的两倍，利用所学解析几何知识，则有

$\text{d}\Sigma =\pm \left|\begin{array}{ccc}{x}_1& y_1& 1\\ x_2& y_2& 1\\ x_3& y_3& 1\end{array}\right|$，符号的选取使 $\text{d}\Sigma >0$，

将 $x_i,y_i\left(i=1,2,3\right)$ 的表达式带入到 $\text{d}\Sigma$ 并忽略高阶无穷小量得

$\begin{array}{c}\text{d}\Sigma =\pm \left|\begin{array}{cc}x\left(u,v\right)& \begin{array}{cc}y\left(u,v\right)& 1\end{array}\\ \begin{array}{c}x\left(u,v\right)+\frac{\partial x}{\partial u}\text{d}u\\ x\left(u,v\right)+\frac{\partial x}{\partial u}\text{d}u+\frac{\partial x}{\partial v}\text{d}v\end{array}& \begin{array}{cc}y\left(u,v\right)+\frac{\partial y}{\partial u}\text{d}u& 1\\ y\left(u,v\right)+\frac{\partial y}{\partial u}\text{d}u+\frac{\partial x}{\partial v}\text{d}v& 1\end{array}\end{array}\right|\\ =\pm \left|\begin{array}{cc}\begin{array}{c}x\\ \frac{\partial x}{\partial u}\text{d}u\end{array}& \begin{array}{cc}y& 1\\ \frac{\partial y}{\partial u}\text{d}u& 0\end{array}\\ \frac{\partial x}{\partial v}\text{d}v& \begin{array}{cc}\frac{\partial x}{\partial v}\text{d}v& 0\end{array}\end{array}\right|,\end{array}$

因此 $\text{d}x\text{d}y=\left|\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)}\right|\text{d}u\text{d}v$，即面积之比 $\frac{\text{d}x\text{d}y}{\text{d}u\text{d}v}=\left|\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)}\right|=\left|J\left(u,v\right)\right|$，所以 $\mu \left(D\right)={\displaystyle \underset{D}{\iint }\text{d}x\text{d}y}={\displaystyle \underset{\Delta }{\iint }\left|J\left(u,v\right)\right|\text{d}u\text{d}v}$。

2.4. 二重积分的变量变换

定理3 设在 $f\left(x,y\right)$ 有界闭区域D上可积，变换 $T:x=x\left(u,v\right)$， $y=y\left(u,v\right)$ 将 $uv$ 平面上按段光滑的封闭的曲线所围成的闭区域 $\text{Δ}$ 一对一的映射成 $xy$ 平面上的闭区域D，函数 $x\left(u,v\right)$， $y\left(u,v\right)$ 在 $\text{Δ}$ 内分别具有一阶连续偏导数且它们的函数行列式

$J\left(u,v\right)=\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)}\ne 0,\left(u,v\right)\in \text{Δ,}$

则有

${\displaystyle \underset{D}{\iint }f\left(x,y\right)}\text{d}x\text{d}y={\displaystyle \underset{\Delta }{\iint }f\left(x\left(u,v\right),y\left(u,v\right)\right)}\left|J\left(u,v\right)\right|\text{d}u\text{d}v.$

推论1 当积分区域是圆域或者圆域的一部分，或者是 $f\left(x^2+y^2\right)$ 时使用极坐标变换

$T:x=r\cos \theta ,y=r\sin \theta 0\le r<+\infty ,0\le \theta <2\text{π}$

变换T的函数行列式为 $J\left(u,v\right)=\left|\begin{array}{cc}\cos \theta & -r\sin \theta \\ \sin \theta & r\cos \theta \end{array}\right|=r$，由引理可知 $xy$ 平面中二重积分的面积微元 $\text{d}x\text{d}y$ 与 $r\theta$ 平面中的面积微元 $\text{d}r\text{d}\theta$ 之间的关系为 $\text{d}x\text{d}y=r\text{d}r\text{d}\theta$，则有

${\displaystyle \underset{D}{\iint }f\left(x,y\right)\text{d}x\text{d}y}={\displaystyle \underset{\Delta }{\iint }f\left(r\cos \theta ,r\sin \theta \right)}\left|J\left(r,\theta \right)\right|\text{d}r\text{d}\theta .$

推论2 与极坐标相似，当我们作广义极坐标变换

$T:\{\begin{array}{c}x=ar\cos \theta ,\\ y=br\sin \theta ,\end{array}0\le r<+\infty ,0\le \theta <2\text{π}$

此时变换T的函数行列式为 $J\left(u,v\right)=\left|\begin{array}{cc}a\cos \theta & -ar\sin \theta \\ b\sin \theta & br\cos \theta \end{array}\right|=abr$，同理有 $\text{d}x\text{d}y=abr\text{d}r\text{d}\theta$，则有

${\displaystyle \underset{D}{\iint }f\left(x,y\right)}\text{d}x\text{d}y={\displaystyle \underset{\Delta }{\iint }f\left(ar\cos \theta ,br\sin \theta \right)}abr\text{d}r\text{d}\theta .$

2.5. 三重积分的变量变换法(与二重积分类似)

定理4 设 $f\left(x,y,z\right)$ 是定义在三维空间可以求解体积的有界闭区域V上的函数，在变换 $T:x=x\left(u,v,w\right)$， $y=y\left(u,v,w\right)$， $z=z\left(u,v,w\right)$ 下将uvw空间的闭区域 $V^{\prime }$ 一对一的变换为xyz空间区域V，且函数 $x\left(u,v,w\right)$， $y\left(u,v,w\right)$， $z\left(u,v,w\right)$ 在 $V^{\prime }$ 内有连续的偏导数，变换T的函数行列式为

$J\left(u,v,w\right)=\frac{\partial \left(x,y,z\right)}{\partial \left(u,v,w\right)}=\left|\begin{array}{ccc}\frac{\partial x}{\partial u}& \frac{\partial x}{\partial v}& \frac{\partial x}{\partial w}\\ \frac{\partial y}{\partial u}& \frac{\partial y}{\partial v}& \frac{\partial y}{\partial w}\\ \frac{\partial z}{\partial u}& \frac{\partial z}{\partial v}& \frac{\partial z}{\partial w}\end{array}\right|\ne 0,\left(u,v,w\right)\in V^{\prime }$

那么函数 $f\left(x,y,z\right)$ 在 $xyz$ 空间的体积微元 $\text{d}x\text{d}y\text{d}z$ 与 $uvw$ 空间体积微元 $\text{d}u\text{d}v\text{d}w$ 之间的关系为

$\text{d}x\text{d}y\text{d}z=\left|J\left(u,v,w\right)\right|\text{d}u\text{d}v\text{d}w$

则有

${\displaystyle \underset{V}{\iiint }f\left(x,y,z\right)}\text{d}x\text{d}y\text{d}z={\displaystyle \underset{V^{\prime }}{\iiint }f\left(x\left(u,v,w\right),y\left(u,v,w\right),z\left(u,v,w\right)\right)}\left|J\left(u,v,w\right)\right|\text{d}u\text{d}v\text{d}w.$ (6)

推论1 在柱面坐标变换下有

$T:\{\begin{array}{c}x=r\cos \theta ,\\ y=r\sin \theta ,\\ z=z,\begin{array}{cc}& \end{array}\end{array}\begin{array}{c}\\ \\ \end{array}\begin{array}{c}0\le r<+\infty ,\begin{array}{c}\end{array}\\ 0\le \theta \le 2\text{π},\begin{array}{c}\end{array}\\ \begin{array}{c}\end{array}-\infty <z<+\infty .\end{array}$

所对应的函数行列式

$J\left(r,\theta ,z\right)=\left|\begin{array}{ccc}\cos \theta & -r\sin \theta & 0\\ \sin \theta & r\cos \theta & 0\\ 0& 0& 1\end{array}\right|=r,$

按照(6)式，三重积分的柱面坐标变换公式为

${\displaystyle \underset{V}{\iiint }f\left(x,y,z\right)}\text{d}x\text{d}y\text{d}z={\displaystyle \underset{V^{\prime }}{\iiint }f\left(r\cos \theta ,r\sin \theta ,z\right)}r\text{d}r\text{d}\theta \text{d}z,$

式中的 $f\left(x,y,z\right)$ 可求体积， $V^{\prime }$ 为V在柱面坐标变换下的原象。

推论2 在球坐标变换下有

$T:\{\begin{array}{ll}x=r\cos \phi \cos \theta ,\hfill & 0\le r<+\infty ,\hfill \\ y=r\cos \phi \sin \theta ,\hfill & 0\le \theta \le 2\text{π},\hfill \\ z=r\sin \phi ,\hfill & -\frac{\text{π}}{\text{2}}\le \phi \le \frac{\text{π}}{\text{2}}.\hfill \end{array}$

所对应的函数行列式为

$J\left(r,\phi ,\theta \right)=\left|\begin{array}{ccc}\cos \phi \cos \theta & -r\sin \phi \cos \theta & -r\cos \phi \sin \theta \\ \cos \phi \sin \theta & -r\sin \phi \cos \theta & r\cos \phi \cos \theta \\ \sin \phi & r\cos \phi & 0\end{array}\right|=r^2\cos \phi$,

按照式(6)，球坐标变换下的公式为

${\displaystyle \underset{V}{\iint }f\left(x,y,z\right)}\text{d}x\text{d}y\text{d}z={\displaystyle \underset{V^{\prime }}{\iint }f\left(r\cos \phi \cos \theta ,r\cos \phi \sin \theta ,r\sin \phi \right)}{r}^2\cos \phi \text{d}r\text{d}\phi \text{d}\theta$,

式中的 $f\left(x,y,z\right)$ 可求体积， $V^{\prime }$ 为V在柱面坐标变换下的原象。

推论3 在广义球坐标变换下有

$T:\{\begin{array}{c}x=ar\sin \phi \cos \theta ,\\ y=br\sin \phi \sin \theta ,\\ z=cr\cos \phi ,\begin{array}{cc}& \end{array}\end{array}\begin{array}{c}\\ \\ \end{array}\begin{array}{c}0\le r<+\infty ,\begin{array}{c}\end{array}\\ 0\le \theta \le 2\text{π},\begin{array}{c}\end{array}\\ \text{0}\le \phi \le \text{π}.\begin{array}{c}\end{array}\end{array}$

所对应的函数行列式为

$J\left(r,\phi ,\theta \right)=\left|\begin{array}{ccc}a\sin \phi \cos \theta & ar\cos \phi \cos \theta & -ar\sin \phi \sin \theta \\ b\sin \phi \sin \theta & br\cos \phi \sin \theta & br\sin \phi \cos \theta \\ c\cos \phi & -cr\sin \phi & 0\end{array}\right|=abc{r}^2\sin \phi$,

按照式(6)，三重积分的在广义球坐标变换公式为

${\displaystyle \underset{V}{\iint }f\left(x,y,z\right)}\text{d}x\text{d}y\text{d}z={\displaystyle \underset{V^{\prime }}{\iint }f\left(ar\sin \phi \cos \theta ,br\sin \phi \sin \theta ,cr\cos \phi \right)}abc{r}^2\sin \phi \text{d}r\text{d}\phi \text{d}\theta ,$

式中的 $f\left(x,y,z\right)$ 可求体积， $V^{\prime }$ 为V在广义球坐标变换下的原象。

2.6. 曲面的面积

定义2.6.1 设曲面S由方程 $z=f\left(x,y\right)$， $\left(x,y\right)\in D$ 确定，其中D是平面上可以求面积的有界区域， $f\left(x,y\right)$ 在D上具有连续的一阶偏导数，则曲面S的面积为

$\Delta S={\displaystyle \underset{D}{\iint }\sqrt{1+f_x^2\left(x,y\right)+f_y^2\left(x,y\right)}}\text{d}x\text{d}y$ (7)

还可以称 $\text{d}S=\sqrt{1+f_x^2\left(x,y\right)+f_y^2\left(x,y\right)}\text{d}x\text{d}y$ 为曲面S的面积微元。

定义2.6.2 设曲面S由参数方程

$x=x\left(u,v\right),y=y\left(u,v\right),z=z\left(u,v\right),\left(u,v\right)\in D$

确定，其中函数 $x\left(u,v\right)$， $y\left(u,v\right)$， $z\left(u,v\right)$ 在D上具有连续的一阶偏导数，且Jacobi行列式

$\left(\begin{array}{ccc}{x}_u& y_u& z_u\\ x_v& y_v& z_v\end{array}\right)$

的秩为2，如果设曲面S无重点，由隐函数存定理，曲面S某点 $P_0\left(x_0,y_0,z_0\right)$ 的邻域可表示为 $x=x$， $y=y$， $z=z\left(x,y\right)$ 的形式，且有

$\frac{\partial z}{\partial x}=-\frac{\partial \left(y,z\right)}{\partial \left(u,v\right)}/\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)},\frac{\partial z}{\partial y}=-\frac{\partial \left(z,x\right)}{\partial \left(u,v\right)}/\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)},$

若D在 $xy$ 平面上的相应区域为 $D_1$，由(7)式曲面S的面积为

$\begin{array}{c}\frac{\partial z}{\partial x}=-\frac{\partial \left(y,z\right)}{\partial \left(u,v\right)}/\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)},\frac{\partial z}{\partial y}=-\frac{\partial \left(z,x\right)}{\partial \left(u,v\right)}/\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)},\\ ={\displaystyle \underset{D}{\iint }\sqrt{1+{\left(-\frac{\partial \left(y,z\right)}{\partial \left(u,v\right)}/\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)}\right)}^2+{\left(-\frac{\partial \left(z,x\right)}{\partial \left(u,v\right)}/\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)}\right)}^2}}\cdot \left|\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)}\right|\text{d}u\text{d}v\\ ={\displaystyle \underset{D}{\iint }\sqrt{{\left(\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)}\right)}^2+{\left(\frac{\partial \left(y,z\right)}{\partial \left(u,v\right)}\right)}^2+{\left(\frac{\partial \left(z,x\right)}{\partial \left(u,v\right)}\right)}^2}}\text{d}u\text{d}v\\ ={\displaystyle \underset{D}{\iint }\sqrt{\left(x_u^2+y_u^2+z_u^2\right)\left(x_v^2+y_v^2+z_v^2\right)-\left(x_u{x}_v+y_u{y}_v+z_u{z}_v\right)}}\text{d}u\text{d}v\end{array}$

记 $E=x_u^2+y_u^2+z_u^2$， $F=x_u{x}_v+y_u{y}_v+z_u{z}_v$， $G=x_v^2+y_v^2+z_v^2$，则有

$\Delta S={\displaystyle \underset{D}{\iint }\sqrt{EG-F^2}}\text{d}u\text{d}v$.

其中 $\sqrt{EG-F^2}\text{d}u\text{d}v$ 为曲面S的面积微元。

定理5 设光滑曲面S由方程 $z=f\left(x,y\right)$ 定义在有界平面区域D上， $f\left(x,y,z\right)$ 为S上的连续函数，则

${\displaystyle \underset{S}{\iint }f\left(x,y,z\right)\text{d}S}={\displaystyle \underset{D}{\iint }\sqrt{1+f_x^2\left(x,y\right)+f_y^2\left(x,y\right)}}\text{d}x\text{d}y$.

推论 由参数形式表示的光滑曲面

$S:\{\begin{array}{c}x=x\left(u,v\right),\\ y=y\left(u,v\right),\\ z=z\left(u,v\right),\end{array}\left(u,v\right)\in D,$

则在曲面S上第一曲面积分的计算公式为

${\displaystyle \underset{S}{\iint }f\left(x,y,z\right)\text{d}S}={\displaystyle \underset{D}{\iint }f\left(x\left(u,v\right),y\left(u,v\right),z\left(u,v\right)\right)\sqrt{EG-F^2}}\text{d}u\text{d}v,$

其中 $E=x_u^2+y_u^2+z_u^2$， $F=x_u{x}_v+y_u{y}_v+z_u{z}_v$， $G=x_v^2+y_v^2+z_v^2$，除此之外还要求雅克比行列式 $\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)}$， $\frac{\partial \left(y,z\right)}{\partial \left(u,v\right)}$， $\frac{\partial \left(z,x\right)}{\partial \left(u,v\right)}$ 中至少有一个不为零。

3. 外积与Jacobi行列式的关系

本节从外积的角度对积分变换的内容进行直观的阐述，更有利于我们的理解，相关内容可参考教材 [3]。

3.1. 关于外积的定义

设 $a=\left(a_1,a_2\right)$， $b=\left(b_1,b_2\right)$ 是平面上两个线性无关的向量，那么由 $a$ 和 $b$ 为邻边的平行四边形的面积是 $\left|\begin{array}{cc}{a}_1& a_2\\ b_1& b_2\end{array}\right|$，它是带有正号或者负的。

如果我们引入一个新的运算符号 $\wedge$ 为： $a\wedge b=\left|\begin{array}{cc}{a}_1& a_2\\ b_1& b_2\end{array}\right|$，它的几何意义就是以 $a$ 和 $b$ 为相邻两边的平行四边形的带有符号的面积。 $\wedge$ 具有以下性质：

1) 重线性：假设 $a,b,c$ 是三个向量， $\lambda$ 是实数，可以推出

$\begin{array}{l}a\wedge \left(b+c\right)=a\wedge b+a\wedge c,\\ \left(a+b\right)\wedge c=a\wedge c+b\wedge c,\\ \left(\lambda a\right)\wedge b=a\wedge \left(\lambda b\right)=\lambda \left(a\wedge b\right),\end{array}$

2) 反交换性：

$a\wedge b=-b\wedge a,$

从而有

$a\wedge a=0.$

面积所带符号的意义：设A是以 $a$， $b$ 为相邻两边的平行四边形，如果从向量 $a$ 出发在A内旋转到向量 $b$ 是逆时针方向(见图4)，则定义它的面积 $a\wedge b$ 带正号，反之则定义它的面积带负号。

为了验证假设的合理性，我们可以在平面上设定一个直角坐标系，其中x轴和y轴构成了右手系，那么从 $a=\left(a_1,a_2\right)$ 到 $b=\left(b_1,b_2\right)$ 是逆时针的情况下有

$a\wedge b=\left|\begin{array}{cc}{a}_1& a_2\\ b_1& b_2\end{array}\right|>0$,

当从 $a$ 到 $b$ 是逆时针时，上式为负，故假设合理。

Figure 4. A parallelogram with two adjacent sides of a, b

图4. a, b为相邻两边的平行四边形

从图4中可以看出，当 $a\perp b$ 时有

$a\wedge b=\left|a\right|\left|b\right|$,

故在这种情况下，将外积运用到Jacobi行列式中与标准数学分析教材相同。

同样的在 $R^3$ 上也有相同的定义：设 $a=\left(a_1,a_2,a_3\right)$， $b=\left(b_1,b_2,b_3\right)$， $c=\left(c_1,c_2,c_3\right)$ 是平面上两个线性无关的向量。定义

$a\wedge b\wedge c=\left|\begin{array}{ccc}{a}_1& a_2& a_3\\ b_1& b_2& b_3\\ c_1& b_2& c_3\end{array}\right|$,

它的几何意义表示的是由 $a,b,c$ 为相邻的三个棱边的平行六面体的带有符号的体积。 $\wedge$ 在 $R^3$ 中同样也具有重线性和反交换性。

称上面的运算 $\wedge$ 为外积，则它是一个具有重线性和反交换性的运算。

例1 设 $e_1$ 和 $e_2$ 是 $R^2$ 中的两个线性无关的向量， $a_1$ 和 $a_2$ 是任意两个向量，假设

$a_1=a_{11}{e}_1+a_{12}{e}_2,a_2=a_{21}{e}_1+a_{22}{e}_2.$

那么根据有外积的性质有

$\begin{array}{c}{a}_1\wedge a_2=\left(a_{11}{e}_1+a_{12}{e}_2\right)\wedge \left(a_{21}{e}_1+a_{22}{e}_2\right)\\ =a_{11}{a}_{22}{e}_1\wedge e_2+a_{12}{a}_{21}{e}_2\wedge e_1\\ =\left(a_{11}{a}_{22}-a_{12}{a}_{21}\right)e_1\wedge e_2\\ =\left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|e_1\wedge e_2.\end{array}$

几何解释：上式左端表示以向量 $a_1$ 和 $a_2$ 为邻边的平行四边形且带有符号的面积，上式右端中的 $e_1\wedge e_2$ 表示以向量 $e_1$ 和 $e_2$ 为邻边的平行四边形且带有符号的面积。上式右端的行列式表示这两个面积之间带有符号的比例系数。如果从 $a_1$ 到 $a_2$ 和从 $e_1$ 到 $e_2$ 的方向是一致的，例如都是逆时针(或者都是逆时针)方向，那么行列式是正，反之行列式取负值。如果上式两端都取绝对值，那么取了绝对值的行列式就是面积 $\left|a_1\wedge a_2\right|$ 和面积 $\left|e_1\wedge e_2\right|$ 之间的比例系数。

例2 设 $e_1$， $e_2$， $e_3$ 是 $R^3$ 中的三个线性无关的向量， $a_1$， $a_2$， $a_3$ 是任意两个向量，假设

$a_i=a_{i1}{e}_1+a_{i2}{e}_2+a_{i3}{e}_{3}i=1,2,3.$

那么根据有外积的性质有

$\begin{array}{c}{a}_1\wedge a_2\wedge a_3=\left(a_{11}{e}_1+a_{12}{e}_2+a_{13}{e}_3\right)\wedge \left(a_{21}{e}_1+a_{22}{e}_2+a_{23}{e}_3\right)\wedge \left(a_{31}{e}_1+a_{32}{e}_2+a_{33}{e}_3\right)\\ =\left|\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right|e_1\wedge e_2\wedge e_3.\end{array}$

上式右端的行列式表示这两个带有符号的体积之间的比例系数，其中一个是 $a_1\wedge a_2\wedge a_3$，另一个是 $e_1\wedge e_2\wedge e_3$。上式两边同时取绝对值，那么取了绝对值的行列式就是体积 $\left|a_1\wedge a_2\wedge a_3\right|$ 和体积 $\left|e_1\wedge e_2\wedge e_3\right|$ 之间的比例系数。

3.2. 将外积应用到Jacobi行列式中

将 $\text{d}x\wedge \text{d}y$ 看作以无穷小量元素 $\text{d}x$ 和 $\text{d}y$ 为相邻两边的平行四边形的带有符号的面积，在通常的笛卡尔坐标系中 $\text{d}x\wedge \text{d}y$ 带有正号。

例3 设极坐标变换 $T:x=r\cos \theta$， $y=r\sin \theta$，那么有

$\text{d}x=\frac{\partial x}{\partial r}\text{d}r+\frac{\partial x}{\partial \theta }\text{d}\theta =\cos \theta \text{d}r-r\sin \theta \text{d}\theta ,$

$\text{d}y=\frac{\partial y}{\partial r}\text{d}r+\frac{\partial y}{\partial \theta }\text{d}\theta =\sin \theta \text{d}r+r\cos \theta \text{d}\theta ,$

如果将 $\text{d}x$， $\text{d}y$， $\text{d}r$， $\text{d}\theta$ 都看作向量，利用外积的性质有

$\begin{array}{c}\text{d}x\wedge \text{d}y=\left(\cos \theta \text{d}r-r\sin \theta \text{d}\theta \right)\wedge \left(\sin \theta \text{d}r+r\cos \theta \text{d}\theta \right)\\ =r{\cos }^2\theta \text{d}r\wedge \text{d}\theta -r{\sin }^2\theta \text{d}\theta \wedge \text{d}r\\ =\left|\begin{array}{cc}\cos \theta & -r\sin \theta \\ \sin \theta & r\cos \theta \end{array}\right|\text{d}r\wedge \text{d}\theta \\ =r\left({\cos }^2\theta +{\sin }^2\theta \right)\text{d}r\wedge \text{d}\theta \\ =r\text{d}r\wedge \text{d}\theta .\end{array}$

几何意义：在笛卡尔坐标系中以 $\text{d}x$ 和 $\text{d}y$ 为相邻两边的无穷小平行四边形的面积也就是直角坐标系中的面积微元，经过极坐标变换变为 $r\text{d}r\wedge \text{d}\theta$，称 $\text{d}r\wedge \text{d}\theta$ 为极坐标系下的面积微元，其中 $\text{d}r\wedge \text{d}\theta$ 总是正的，r是两个面积之间的比例系数也就函数行列式的绝对值。

定义3.2.1 设变换 $T:x=x\left(u,v\right)$， $y=y\left(u,v\right)$，其中 $\left(u,v\right)\in D^{\prime }$， $\left(x,y\right)\in D$，并且假设

1) 函数 $x\left(u,v\right)$， $y\left(u,v\right)$ 将区域 $D$ 和 $D^{\prime }$ 一一对应；

2) 函数 $x\left(u,v\right)$， $y\left(u,v\right)$ 在区域 $D^{\prime }$ 内具有连续的一阶偏导数，且它们的逆映射 $u=u\left(x,y\right)$， $v=v\left(x,y\right)$ 在区域 $D$ 内也具有连续的一阶偏导数。

3) 变换 $T$ 的函数行列式

$J=\left|\begin{array}{cc}{x}_u& x_v\\ y_u& y_v\end{array}\right|\ne 0,\left(u,v\right)\in D^{\prime },$

则称这个变换是从区域 $D$ 到 $D^{\prime }$ 的正则变换。

因为 $\text{d}x=x_u\text{d}u+x_v\text{d}v$， $\text{d}y=y_u\text{d}u+y_v\text{d}v$，所以有

$\begin{array}{c}\text{d}x\wedge \text{d}y=\left(x_u\text{d}u+x_v\text{d}v\right)\wedge \left(y_u\text{d}u+y_v\text{d}v\right)\\ =x_u{y}_v\text{d}u\wedge \text{d}v+x_v{y}_u\text{d}v\wedge \text{d}u\\ =\left|\begin{array}{cc}{x}_u& x_v\\ y_u& y_v\end{array}\right|\text{d}u\wedge \text{d}v\\ =\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)}\text{d}u\wedge \text{d}v.\end{array}$

几何解释：假设 $\text{d}x\wedge \text{d}y$ 和 $\text{d}u\wedge \text{d}v$ 均取正号，那么在正则变换下直角坐标系中的面积元素 $\text{d}x\wedge \text{d}y$ 可变换为曲面坐标系下的面积元素 $\left|\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)}\right|\text{d}u\wedge \text{d}v$，其中 $\left|\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)}\right|$ 是变换 $x=x\left(u,v\right)$， $y=y\left(u,v\right)$ 的函数行列式的绝对值。

3.3. 二重积分变换

定理1 设 $D$ 是 $xy$ 平面上可求面积的区域，函数 $f\left(x,y\right)$ 在 $D$ 上连续可积分，存在变换

$T:x=x\left(u,v\right),y=y\left(u,v\right),\left(u,v\right)\in D^{\prime }$

是从 $D$ 到 $D^{\prime }$ 的正则变换，那么在直角坐标系下的面积元素变换成为曲面坐标系下的面积元素 $\left|\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)}\right|\text{d}u\wedge \text{d}v$，取绝对值保证面积取正，则有

${\displaystyle \underset{D}{\iint }f\left(x,y\right)}\text{d}x\text{d}y={\displaystyle \underset{D^{\prime }}{\iint }f\left(x\left(u,v\right),y\left(u,v\right)\right)}\left|\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)}\right|\text{d}u\text{d}v.$ (8)

推论1作极坐标变换

$T:\{\begin{array}{c}x=r\cos \theta ,\\ y=r\sin \theta ,\end{array}0\le r<+\infty ,0\le \theta <2\text{π}$

则由(8)式可得出

${\displaystyle \underset{D}{\iint }f\left(x,y\right)}\text{d}x\text{d}y={\displaystyle \underset{D^{\prime }}{\iint }f\left(r\cos \theta ,r\sin \theta \right)}r\text{d}r\text{d}\theta .$

推论2作广义极坐标变换

$T:\{\begin{array}{c}x=ar\cos \theta ,\\ y=br\sin \theta ,\end{array}0\le r<+\infty ,0\le \theta <2\text{π}$

坐标代换下Jacobi行列式 $\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)}=abr$，则由(8)式可得出

${\displaystyle \underset{D}{\iint }f\left(x,y\right)}\text{d}x\text{d}y={\displaystyle \underset{D^{\prime }}{\iint }f\left(ar\cos \theta ,br\sin \theta \right)}abr\text{d}r\text{d}\theta .$

3.4. 三重积分的坐标变换

定理2 设三重积分 ${\displaystyle \iiint f\left(x,y,z\right)}\text{d}x\text{d}y\text{d}z$ 作坐标变换 $T:x=x\left(u,v,w\right)$， $y=y\left(u,v,w\right)$， $z=z\left(u,v,w\right)$， $\left(u,v,w\right)\in V^{\prime }$，并要求这一变换是正则变换即满足条件

1) 函数 $x\left(u,v,w\right)$， $y\left(u,v,w\right)$， $z\left(u,v,w\right)$ 将区域 $V$ 与区域 $V^{\prime }$ 一一对应；

2) 函数 $x\left(u,v,w\right)$， $y\left(u,v,w\right)$， $z\left(u,v,w\right)$ 在区域 $V^{\prime }$ 内具有连续的一阶偏导数，且它们的逆映射 $u=u\left(x,y,z\right)$， $v=v\left(x,y,z\right)$， $w=w\left(x,y,z\right)$ 在区域 $V$ 内也具有连续的一阶偏导数；

3) 变换T的函数行列式

$J=\frac{\partial \left(x,y,z\right)}{\partial \left(u,v,w\right)}=\left|\begin{array}{ccc}{x}_u& x_v& x_w\\ y_u& y_v& y_w\\ z_u& z_v& z_w\end{array}\right|\ne 0$

此时积分区间由 $V$ 变换为 $V^{\prime }$，直角坐标系下的体积元素 $\text{d}x\text{d}y\text{d}z$ 变换为

$\begin{array}{c}\text{d}x\wedge \text{d}y\wedge \text{d}z=\left(x_u\text{d}u+x_v\text{d}v+x_w\text{d}w\right)\wedge \left(x_u\text{d}u+x_v\text{d}v+x_w\text{d}w\right)\wedge \left(x_u\text{d}u+x_v\text{d}v+x_w\text{d}w\right)\\ =\left|\begin{array}{ccc}{x}_u& x_v& x_w\\ y_u& y_v& y_w\\ z_u& z_v& z_w\end{array}\right|\text{d}u\wedge \text{d}v\wedge \text{d}w\\ =\frac{\partial \left(x,y,z\right)}{\partial \left(u,v,w\right)}\text{d}u\wedge \text{d}v\wedge \text{d}w,\end{array}$

称 $\left|\frac{\partial \left(x,y,z\right)}{\partial \left(u,v,w\right)}\right|\text{d}u\text{d}v\text{d}w$ 是曲面坐标系中的体积元素，所以有

${\displaystyle \underset{V}{\iiint }f\left(x,y,z\right)}\text{d}x\text{d}y\text{d}z={\displaystyle \underset{V^{\prime }}{\iiint }f\left(x\left(u,v,w\right),y\left(u,v,w\right),z\left(u,v,w\right)\right)}\left|\frac{\partial \left(x,y,z\right)}{\partial \left(u,v,w\right)}\right|\text{d}u\text{d}v\text{d}w.$

推论1 作柱坐标变换

$T:\{\begin{array}{c}x=r\cos \theta ,\\ y=r\sin \theta ,\\ z=z,\begin{array}{cc}& \end{array}\end{array}\begin{array}{c}\\ \\ \end{array}\begin{array}{c}0\le r<+\infty \begin{array}{c}\end{array}\\ 0\le \theta \le 2\text{π},\begin{array}{c}\end{array}\\ \begin{array}{c}\end{array}-\infty <z<+\infty .\end{array}$

在柱坐标变换下的体积元素为

$\left|\frac{\partial \left(x,y,z\right)}{\partial \left(r,\theta ,z\right)}\right|\text{d}r\text{d}\theta \text{d}z=r\text{d}r\text{d}\theta \text{d}z$.

推论2 作球坐标变换

$T:\{\begin{array}{ll}x=r\cos \phi \cos \theta ,\hfill & 0\le r<+\infty ,\hfill \\ y=r\cos \phi \sin \theta ,\hfill & 0\le \theta \le 2\text{π},\hfill \\ z=r\sin \phi ,\hfill & -\frac{\text{π}}{\text{2}}\le \phi \le \frac{\text{π}}{2}.\hfill \end{array}$

在球坐标变换下，体积元素为

$\left|\frac{\partial \left(x,y,z\right)}{\partial \left(r,\phi ,\theta \right)}\right|\text{d}r\text{d}\phi \text{d}\theta =r^2\cos \phi \text{d}r\text{d}\phi \text{d}\theta .$

4. 内积、Riemann度量与Jacobi行列式的关系

这部分内容将积分变换与向量内积和外积联系到一起，运用到Riemann度量的知识，是求取体积元几何与Jacobi行列式的另一种方法，一些相关的知识来源可以参考教材 [4] [5] [6]。

4.1. 向量的数量积和向量积

定义4.1.1 两个向量 $a$ 和 $b$ 的模和它们夹角的余弦的乘积叫做向量 $a$ 和 $b$ 的数量积或称内积，记做 $a\cdot b$ 或 $ab$，即

$a\cdot b=\left|a\right|\left|b\right|\cos \angle \left(a,b\right).$

定义4.1.2 两向量 $a$ 与 $b$ 的向量积或称外积是一个向量，记作 $a\times b$ 或 $\left[ab\right]$，它的模是

$\left|a\times b\right|=\left|a\right|\left|b\right|\sin \angle \left(a,b\right).$

已知三角函数公式 ${\sin }^2\theta +{\cos }^2\theta =1$，我们可以推出 $\sin \theta =\sqrt{1-{\cos }^2\theta }$。若记 $\angle \left(a,b\right)=\theta$，根据内积公式有 $\cos \angle \left(a,b\right)=\frac{a\cdot b}{\left|a\right|\left|b\right|}$，那么

$\left|a\times b\right|=\left|a\right|\left|b\right|\sin \theta =\left|a\right|\left|b\right|\sqrt{1-{\left(\frac{a\cdot b}{\left|a\right|\left|b\right|}\right)}^2}=\sqrt{{\left|a\right|}^2{\left|b\right|}^2-{\left(a\cdot b\right)}^2}=\sqrt{\left|\left(\begin{array}{cc}a\cdot a& a\cdot b\\ b\cdot a& b\cdot b\end{array}\right)\right|}=\sqrt{\left|A\right|},$

式中记 $A=\left(\begin{array}{cc}a\cdot a& a\cdot b\\ b\cdot a& b\cdot b\end{array}\right)=\left(\begin{array}{c}a\\ b\end{array}\right)\left(\begin{array}{cc}a& b\end{array}\right)$。

需要指出的是我们所介绍的向量运算的定义与运算规律，是和坐标系的选取没有关系的，但是选取不同的坐标系将对应不同的向量运算表达式。

例如 两个向量 $a$ 、 $b$ 的内积在直角坐标系下为

$a\cdot b=X_1{X}_2+Y_1{Y}_2$

其中 $X_1$ 、 $Y_1$ 与 $X_2$ 、 $Y_2$ 分别是向量 $a$ 与 $b$ 的直角坐标。如果选取一般的坐标系，设

$a=X_1{e}_1+Y_1{e}_2,b=X_2{e}_1+Y_2{e}_2,$

由内积的运算规律有

$a\cdot b=X_1{X}_2{e}_1^2+Y_1{Y}_2{e}_2^2+\left(X_1{Y}_2+Y_1{X}_2\right)e_1\cdot e_2=\left(\begin{array}{cc}{X}_1& Y_2\end{array}\right)\left(\begin{array}{cc}{e}_1\cdot e_1& e_1\cdot e_2\\ e_2\cdot e_1& e_2\cdot e_2\end{array}\right)\left(\begin{array}{c}{X}_2\\ Y_2\end{array}\right)$

上式中

$A=\left(\begin{array}{cc}{e}_1\cdot e_1& e_1\cdot e_2\\ e_2\cdot e_1& e_2\cdot e_2\end{array}\right)=\left(\begin{array}{c}{e}_1\\ e_2\end{array}\right)\left(\begin{array}{cc}{e}_1& e_2\end{array}\right).$

4.2. 将内积、Riemann度量应用到Jacobi行列式

定理1 设光滑曲面S由方程 $r=r\left(x,y\right)$ 或变换 $T:x=x\left(u,v\right)$， $y=y\left(u,v\right)$ 给出，变换T将 $uv$ 平面上按段光滑的封闭的曲线所围成的闭区域 $\text{Δ}$ 一对一的映射成 $xy$ 平面上的闭区域D，函数 $x\left(u,v\right)$， $y\left(u,v\right)$ 在 $\text{Δ}$ 内具有一阶连续偏导数且它们的Jacobi行列式为

$J\left(u,v\right)=\frac{\partial \left(x,y\right)}{\partial \left(u,v\right)}=\sqrt{\left|A\right|}\ne 0,\left(u,v\right)\in \text{Δ},$

则 $\text{Δ}$ 和 $xy$ 平面上的对应区域D之间的微元面积伸缩系数为 $\sqrt{\left|A\right|}$，即

$\left|\text{d}r\right|=\text{d}x\text{d}y=\sqrt{\left|A\right|}\text{d}u\text{d}v$

证明 由参数方程 $x=x\left(u,v\right)$， $y=y\left(u,v\right)$ 及方程 $r=r\left(x,y\right)$ 知

$\text{d}x=\frac{\partial x}{\partial u}\text{d}u+\frac{\partial x}{\partial v}\text{d}v,$

$\text{d}x=\frac{\partial x}{\partial u}\text{d}u+\frac{\partial x}{\partial v}\text{d}v,$

$\frac{\partial r}{\partial u}=\frac{\partial r}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial r}{\partial y}\frac{\partial y}{\partial u},$

$\frac{\partial r}{\partial v}=\frac{\partial r}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial r}{\partial y}\frac{\partial y}{\partial v},$

根据一阶微分形式的不变性，得

$\begin{array}{c}\text{d}r=r_x\text{d}x+r_y\text{d}y=r_x\left(\frac{\partial x}{\partial u}\text{d}u+\frac{\partial x}{\partial v}\text{d}v\right)+r_y\left(\frac{\partial y}{\partial u}\text{d}u+\frac{\partial y}{\partial v}\text{d}v\right)\\ =\left(\frac{\partial r}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial r}{\partial y}\frac{\partial y}{\partial u}\right)\text{d}u+\left(\frac{\partial r}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial r}{\partial y}\frac{\partial y}{\partial v}\right)\text{d}v=\frac{\partial r}{\partial u}\text{d}u+\frac{\partial r}{\partial v}\text{d}v=e_1\text{d}u+e_2\text{d}v\end{array}$

式中记 $\frac{\partial r}{\partial u}=e_1$， $\frac{\partial r}{\partial v}=e_2$。

又

$\begin{array}{c}\text{d}r\cdot \text{d}r=\left(e_1\text{d}u+e_2\text{d}v\right)\cdot \left(e_1\text{d}u+e_2\text{d}v\right)\\ =\left(\begin{array}{cc}\text{d}u& \text{d}v\end{array}\right)\left(\begin{array}{c}{e}_1\\ e_2\end{array}\right)\left(\begin{array}{cc}{e}_1& e_2\end{array}\right)\left(\begin{array}{c}\text{d}u\\ \text{d}v\end{array}\right)\\ =\left(\begin{array}{cc}\text{d}u& \text{d}v\end{array}\right)\left(\begin{array}{cc}{e}_1\cdot e_1& e_1\cdot e_2\\ e_2\cdot e_1& e_2\cdot e_2\end{array}\right)\left(\begin{array}{c}\text{d}u\\ \text{d}v\end{array}\right)\\ =\left(\begin{array}{cc}\text{d}u& \text{d}v\end{array}\right)A\left(\begin{array}{c}\text{d}u\\ \text{d}v\end{array}\right)\end{array}$

式中记

$A=\left(\begin{array}{cc}{e}_1\cdot e_1& e_1\cdot e_2\\ e_2\cdot e_1& e_2\cdot e_2\end{array}\right),$

所以有

$\left|\text{d}r\right|=\text{d}x\text{d}y=\sqrt{\left|A\right|}\text{d}u\text{d}v$.

推论1 设光滑曲面S由方程 $r=r\left(x,y\right)$ 给出，又 $f\left(x,y\right)$ 在S上连续，并存在极坐标变换

$T:\{\begin{array}{c}x=\rho \cos \theta ,\\ y=\rho \sin \theta ,\end{array}0\le \rho <+\infty ,0\le \theta <2\text{π}$

且函数 $x,y$ 满足定理1中的条件，若记 $e_1=\frac{\partial r}{\partial \rho }=\left(\begin{array}{c}\cos \theta \\ \sin \theta \end{array}\right)$， $e_2=\frac{\partial r}{\partial \theta }=\left(\begin{array}{c}-\rho \sin \theta \\ \rho \cos \theta \end{array}\right)$，由定理1则有

$A=\left(\begin{array}{cc}{e}_1\cdot e_1& e_1\cdot e_2\\ e_2\cdot e_1& e_2\cdot e_2\end{array}\right)=\left(\begin{array}{cc}1& 0\\ 0& {\rho }^2\end{array}\right)$.

那么变换T的函数行列式为 $J\left(u,v\right)=\sqrt{\left|A\right|}=\rho$，故得

${\displaystyle \underset{D}{\iint }f\left(x,y\right)}\text{d}x\text{d}y={\displaystyle \underset{\Delta }{\iint }f\left(r\cos \theta ,r\sin \theta \right)}\rho \text{d}\rho \text{d}\theta .$

推论2 设光滑曲面S由方程 $r=r\left(x,y\right)$ 给出，又 $f\left(x,y\right)$ 在S上连续并存在广义极坐标变换

$T:\{\begin{array}{c}x=a\rho \cos \theta ,\\ y=b\rho \sin \theta ,\end{array}0\le r<+\infty ,0\le \theta <2\text{π}$

且函数 $x,y$ 满足定理1中的条件，若记 $e_1=\frac{\partial r}{\partial \rho }=\left(\begin{array}{c}a\cos \theta \\ b\sin \theta \end{array}\right)$， $e_2=\frac{\partial r}{\partial \theta }=\left(\begin{array}{c}-a\rho \sin \theta \\ b\rho \cos \theta \end{array}\right)$，由定理1则有

$A=\left(\begin{array}{cc}{e}_1\cdot e_1& e_1\cdot e_2\\ e_2\cdot e_1& e_2\cdot e_2\end{array}\right)=a^2{b}^2{\rho }^2,$

那么变换T的函数行列式为 $J\left(u,v\right)=\sqrt{\left|A\right|}=\rho ab$，得

${\displaystyle \underset{D}{\iint }f\left(x,y\right)}\text{d}x\text{d}y={\displaystyle \underset{\Delta }{\iint }f\left(r\cos \theta ,r\sin \theta \right)}\rho ab\text{d}\rho \text{d}\theta .$

4.3. 第一型曲面积分

定理2 设光滑曲面S由方程 $r=r\left(x,y,z\right)$ 表示或者由参数方程

$x=x\left(u,v\right),y=y\left(u,v\right),z=z\left(u,v\right),\left(u,v\right)\in D$

确定，其中函数 $x\left(u,v\right)$， $y\left(u,v\right)$， $z\left(u,v\right)$ 在 $D$ 上具有连续的一阶偏导数，且Jacobi行列式

$\left(\begin{array}{ccc}{x}_u& y_u& z_u\\ x_v& y_v& z_v\end{array}\right)$

的秩为2，如果设曲面S上任意一点P处，有一条u-曲线和v-曲线，它们都经过点P， $r_u$ 和 $r_v$ 分别是这两条曲线在P处的切向量，那么 $r_u\text{d}u$ 和 $r_u\text{d}u$ 都应是曲面S在点P得切平面，则 $\left|r_u\text{d}u\right|$ 和 $\left|r_v\text{d}v\right|$ 分别是u-曲线和v-曲线的弧长微分，所以

$\left|r_u\text{d}u\times r_v\text{d}v\right|=\left|r_u\times r_v\right|\text{d}u\text{d}v$

是以 $r_u\text{d}u$ 和 $r_u\text{d}u$ 为相邻两边的平行四边形得面积，称为曲面S的面积元素，记 $\text{d}S$，也就是

$\text{d}S=\left|r_u\times r_v\right|\text{d}u\text{d}v$,

那么曲面S的面积就是

$S={\displaystyle \underset{D}{\int }\left|r_u\times r_v\right|}\text{d}u\text{d}v$.

证明 因为

$r_u=\frac{\partial r}{\partial u}=\frac{\partial r}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial r}{\partial y}\frac{\partial y}{\partial u}+\frac{\partial r}{\partial z}\frac{\partial z}{\partial u},$

$r_v=\frac{\partial r}{\partial v}=\frac{\partial r}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial r}{\partial y}\frac{\partial y}{\partial v}+\frac{\partial r}{\partial z}\frac{\partial z}{\partial v},$

记 $\frac{\partial r}{\partial u}=e_1$， $\frac{\partial r}{\partial v}=e_2$，同定理1证明得

$\begin{array}{c}A=\left(\begin{array}{cc}{e}_1\cdot e_1& e_1\cdot e_2\\ e_2\cdot e_1& e_2\cdot e_2\end{array}\right)\\ =\left(\begin{array}{cc}{x}_u^2+y_u^2+z_u^2& x_u{x}_v+y_u{y}_v+y_u{y}_v\\ x_u{x}_v+y_u{y}_v+y_u{y}_v& x_v^2+y_v^2+z_v^2\end{array}\right)\end{array}$

如果令

$E=e_1\cdot e_1=x_u^2+y_u^2+z_u^2,$

$F=e_1\cdot e_2=x_u{x}_v+y_u{y}_v+z_u{z}_v,$

$G=e_2\cdot e_2=x_v^2+y_v^2+z_v^2,$

所以有 $\left|A\right|=EG-F^2$。

于是曲面S的面积就是

$S={\displaystyle \underset{D}{\iint }\sqrt{EG-F^2}}\text{d}u\text{d}v.$

注 如果光滑得曲面S的方程是 $z=f\left(x,y\right)$， $\left(x,y\right)\in D$，D是 $xy$ 平面上可度量的区域，那么S的方程表示为

$x=x,y=y,z=f\left(x,y\right),\left(x,y\right)\in D$

那么

$r_x=\left(1,0,\frac{\partial f}{\partial x}\right),r_y=\left(0,1,\frac{\partial f}{\partial y}\right),$

$E=r_x\cdot r_x=1+{\left(\frac{\partial f}{\partial x}\right)}^2$,

$F=r_x\cdot r_y=\frac{\partial f}{\partial x}\frac{\partial f}{\partial y}$,

$G=r_y\cdot r_y=1+{\left(\frac{\partial f}{\partial y}\right)}^2,$

所以

$EG-F^2=1+{\left(\frac{\partial f}{\partial x}\right)}^2+{\left(\frac{\partial f}{\partial y}\right)}^2$,

曲面S的面积就是

$S={\displaystyle \underset{D}{\iint }\sqrt{1+{\left(\frac{\partial f}{\partial x}\right)}^2+{\left(\frac{\partial f}{\partial y}\right)}^2}}\text{d}x\text{d}y$.

4.4. 三重积分的坐标变换

定理3设光滑曲面S由方程 $r=r\left(x,y,z\right)$ 表示，又 $f\left(x,y,z\right)$ 在S上连续，并存在坐标变换 $T:x=x\left(u,v,w\right)$， $y=y\left(u,v,w\right)$， $z=z\left(u,v,w\right)$，并要求这一变换是正则变换，其中 $\left(x,y,z\right)\in V$，

$\left(u,v,w\right)\in V^{\prime }$，则 ${\displaystyle \underset{V}{\iiint }f\left(x,y,z\right)}\text{d}x\text{d}y\text{d}z$ 存在，且

${\displaystyle \underset{V}{\iiint }f\left(x,y,z\right)}\text{d}x\text{d}y\text{d}z={\displaystyle \underset{V^{\prime }}{\iiint }f\left(x\left(u,v,w\right),y\left(u,v,w\right),z\left(u,v,w\right)\right)}\sqrt{\left|A\right|}\text{d}u\text{d}v\text{d}w.$

证明 因为

$\begin{array}{l}\text{d}x=\frac{\partial x}{\partial u}\text{d}u+\frac{\partial x}{\partial v}\text{d}v+\frac{\partial x}{\partial w}\text{d}w,\\ \text{d}y=\frac{\partial y}{\partial u}\text{d}u+\frac{\partial y}{\partial v}\text{d}v+\frac{\partial y}{\partial w}\text{d}w,\\ \text{d}z=\frac{\partial z}{\partial u}\text{d}u+\frac{\partial z}{\partial v}\text{d}v+\frac{\partial z}{\partial w}\text{d}w,\end{array}$

又

$\begin{array}{l}\frac{\partial r}{\partial u}=\frac{\partial r}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial r}{\partial y}\frac{\partial y}{\partial u}+\frac{\partial r}{\partial z}\frac{\partial z}{\partial u},\\ \frac{\partial r}{\partial v}=\frac{\partial r}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial r}{\partial y}\frac{\partial y}{\partial v}+\frac{\partial r}{\partial z}\frac{\partial z}{\partial v},\\ \frac{\partial r}{\partial w}=\frac{\partial r}{\partial x}\frac{\partial x}{\partial w}+\frac{\partial r}{\partial y}\frac{\partial y}{\partial w}+\frac{\partial r}{\partial z}\frac{\partial z}{\partial w},\end{array}$

根据一阶微分形式的不变性，有

$\begin{array}{c}\text{d}r=r_x\text{d}x+r_y\text{d}y+r_z\text{d}z\\ =\frac{\partial r}{\partial x}\left(\frac{\partial x}{\partial u}\text{d}u+\frac{\partial x}{\partial v}\text{d}v+\frac{\partial x}{\partial w}\text{d}w\right)+\frac{\partial r}{\partial y}\left(\frac{\partial y}{\partial u}\text{d}u+\frac{\partial y}{\partial v}\text{d}v+\frac{\partial y}{\partial w}\text{d}w\right)\\ \begin{array}{c}\end{array}+\frac{\partial r}{\partial z}\left(\frac{\partial z}{\partial u}\text{d}u+\frac{\partial z}{\partial v}\text{d}v+\frac{\partial z}{\partial w}\text{d}w\right)\end{array}$

$\begin{array}{l}=\left(\frac{\partial r}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial r}{\partial y}\frac{\partial y}{\partial u}+\frac{\partial r}{\partial z}\frac{\partial z}{\partial u}\right)\text{d}u+\left(\frac{\partial r}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial r}{\partial y}\frac{\partial y}{\partial v}+\frac{\partial r}{\partial z}\frac{\partial z}{\partial v}\right)\text{d}v\\ \begin{array}{c}\end{array}+\left(\frac{\partial r}{\partial x}\frac{\partial x}{\partial w}+\frac{\partial r}{\partial y}\frac{\partial y}{\partial w}+\frac{\partial r}{\partial z}\frac{\partial z}{\partial w}\right)\text{d}w\\ =\frac{\partial r}{\partial u}\text{d}u+\frac{\partial r}{\partial v}\text{d}v+\frac{\partial r}{\partial w}\text{d}w=e_1\text{d}u+e_2\text{d}v+e_3\text{d}w,\end{array}$

式中记 $\frac{\partial r}{\partial u}=e_1$， $\frac{\partial r}{\partial v}=e_2$， $\frac{\partial r}{\partial w}=e_3$，

$\begin{array}{c}\text{d}r\cdot \text{d}r=\left(e_1\text{d}u+e_2\text{d}v+e_3\text{d}w\right)\cdot \left(e_1\text{d}u+e_2\text{d}v+e_3\text{d}w\right)\\ =\left(\begin{array}{ccc}\text{d}u& \text{d}v& \text{d}w\end{array}\right)\left(\begin{array}{c}{e}_1\\ e_2\\ e_3\end{array}\right)\left(\begin{array}{ccc}{e}_1& e_2& e_3\end{array}\right)\left(\begin{array}{c}\text{d}u\\ \text{d}v\\ \text{d}w\end{array}\right)\\ =\left(\begin{array}{ccc}\text{d}u& \text{d}v& \text{d}w\end{array}\right)\left(\begin{array}{ccc}{e}_1\cdot e_1& e_1\cdot e_2& e_1\cdot e_3\\ e_2\cdot e_1& e_2\cdot e_2& e_2\cdot e_3\\ e_3\cdot e_1& e_3\cdot e_2& e_3\cdot e_3\end{array}\right)\left(\begin{array}{c}\text{d}u\\ \text{d}v\\ \text{d}w\end{array}\right)\end{array}$

记式中

$A=\left(\begin{array}{ccc}{e}_1\cdot e_1& e_1\cdot e_2& e_1\cdot e_3\\ e_2\cdot e_1& e_2\cdot e_2& e_2\cdot e_3\\ e_3\cdot e_1& e_3\cdot e_2& e_3\cdot e_3\end{array}\right),$

与定理1相似在坐标变换T下的函数行列式 $J\left(u,v,w\right)=\sqrt{\left|A\right|}$，所以有

${\displaystyle \underset{V}{\iiint }f\left(x,y,z\right)}\text{d}x\text{d}y\text{d}z={\displaystyle \underset{V^{\prime }}{\iiint }f\left(x\left(u,v,w\right),y\left(u,v,w\right),z\left(u,v,w\right)\right)}\sqrt{\left|A\right|}\text{d}u\text{d}v\text{d}w.$

推论1 若是定理3中的坐标变换为柱面坐标变换

$T:\{\begin{array}{c}x=\rho \cos \theta ,\\ y=\rho \sin \theta ,\\ z=z,\begin{array}{cc}& \end{array}\end{array}\begin{array}{c}\\ \\ \end{array}\begin{array}{c}0\le \rho <+\infty ,\begin{array}{c}\end{array}\\ 0\le \theta \le 2\text{π},\begin{array}{c}\end{array}\\ \begin{array}{c}\end{array}-\infty <z<+\infty .\end{array}$

那么可以得出

$e_1=\frac{\partial r}{\partial \rho }=\left(\begin{array}{c}\cos \theta \\ \sin \theta \\ 0\end{array}\right),e_2=\frac{\partial r}{\partial \theta }=\left(\begin{array}{c}-\rho \sin \theta \\ \rho \cos \theta \\ 0\end{array}\right),e_3=\frac{\partial r}{\partial z}=\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right),$

经计算可得 $\left|A\right|={\rho }^2$，所以有

${\displaystyle \underset{V}{\iiint }f\left(x,y,z\right)}\text{d}x\text{d}y\text{d}z={\displaystyle \underset{V^{\prime }}{\iiint }f\left(\rho \cos \theta ,\rho \sin \theta ,z\right)}\rho \text{d}\rho \text{d}\theta \text{d}z.$

推论2 若是定理3中的坐标变换为球坐标变换

$T:\{\begin{array}{ll}x=\rho \cos \phi \cos \theta ,\hfill & 0\le \rho <+\infty ,\hfill \\ y=\rho \cos \phi \sin \theta ,\hfill & 0\le \theta \le 2\text{π},\hfill \\ z=\rho \sin \phi ,\hfill & -\frac{\text{π}}{\text{2}}\le \phi \le \frac{\text{π}}{2}.\hfill \end{array}$

那么可以得出

$e_1=\frac{\partial r}{\partial \rho }=\left(\begin{array}{c}\cos \phi \cos \theta \\ \cos \phi \sin \theta \\ \sin \phi \end{array}\right),e_2=\frac{\partial r}{\partial \phi }=\left(\begin{array}{c}-\rho \sin \phi \cos \theta \\ -\rho \sin \phi \sin \theta \\ \rho \cos \phi \end{array}\right),e_3=\frac{\partial r}{\partial \theta }=\left(\begin{array}{c}-\rho \cos \phi \sin \theta \\ \rho \cos \phi \cos \theta \\ 0\end{array}\right),$

经计算可得 $\left|A\right|={\rho }^4{\cos }^2\phi$，所以有

${\displaystyle \underset{V}{\iiint }f\left(x,y,z\right)}\text{d}x\text{d}y\text{d}z={\displaystyle \underset{V^{\prime }}{\iiint }f\left(\rho \cos \phi \cos \theta ,\rho \cos \phi \sin \theta ,\rho \sin \phi \right)}{\rho }^2\cos \phi \text{d}\rho \text{d}\phi \text{d}\theta .$

推论3 若是定理3中的坐标变换为广义球坐标变换

$T:\{\begin{array}{ll}x=a\rho \cos \phi \cos \theta ,\hfill & 0\le \rho <+\infty ,\hfill \\ y=b\rho \cos \phi \sin \theta ,\hfill & 0\le \theta \le 2\text{π},\hfill \\ z=c\rho \sin \phi ,\hfill & -\frac{\text{π}}{\text{2}}\le \phi \le \frac{\text{π}}{2}.\hfill \end{array}$

那么可以得出

$e_1=\frac{\partial r}{\partial \rho }=\left(\begin{array}{c}a\cos \phi \cos \theta \\ b\cos \phi \sin \theta \\ c\sin \phi \end{array}\right),e_2=\frac{\partial r}{\partial \phi }=\left(\begin{array}{c}-a\rho \sin \phi \cos \theta \\ -b\rho \sin \phi \sin \theta \\ c\rho \cos \phi \end{array}\right),e_3=\frac{\partial r}{\partial \theta }=\left(\begin{array}{c}-a\rho \cos \phi \sin \theta \\ b\rho \cos \phi \cos \theta \\ 0\end{array}\right),$

经计算可得 $\left|A\right|=a^2{b}^2{c}^2{\rho }^4{\cos }^2\phi$，所以有

${\displaystyle \underset{V}{\iiint }f\left(x,y,z\right)}\text{d}x\text{d}y\text{d}z={\displaystyle \underset{V^{\prime }}{\iiint }f\left(\rho \cos \phi \cos \theta ,\rho \cos \phi \sin \theta ,\rho \sin \phi \right)abc}{\rho }^2\cos \phi \text{d}\rho \text{d}\phi \text{d}\theta .$