基于事件触发控制带有参数不确定的时滞Lur’e系统主从同步

Master-Slave Synchronization of Time-Delay Lur’e Systems with Parametric Uncertainty Based on the Event-Triggered Mechanism

摘要: 本文研究了参数不确定的时滞Lur’e系统采样数据主从同步问题。为了节约信道资源，引入了非周期事件触发机制，只有在满足触发条件时，当前采样数据才会被传输到网络中。为了减少保守性，充分利用了系统的非线性，引进了合适的三重Lyapunov-Krasovskii (L-K)泛函项，并不要求所有的对称矩阵都是正定矩阵，结合基于辅助函数的积分不等式和逆凸矩阵不等式及Schur补引理，给出了新的线性矩阵不等式形式的同步判据。最后，通过两个Chua’s电路的数值仿真验证了结论的有效性。

Abstract: This paper investigates the master-slave synchronization of sampled-data for delay Lur’e systems with uncertain parameters. In order to save the channel resources, the aperiodic event-triggered mechanism is introduced. Only when the trigger condition is satisfied, the current sampled-data will be transferred to the network. In order to reduce the conservatism and make full use of the nonlinearity of the system, the appropriate triple Lyapunov-Krasovskii functional terms are introduced. It is not required that all symmetric matrices are positive definite matrices. A new synchronization criterion in the form of linear matrix inequalities (LMIs) is given by combining the integral inequality based on auxiliary function, inverse convex matrix inequality and Schur complement lemma. Finally, two numerical simulations of Chua’s circuit are provided to show the effectiveness of the conclusion.

1. 引言

混沌系统是一种典型的非线性系统，在航空航天、保密通信、生态系统、生物工程、图像处理等领域得到广泛应用。同步是混沌系统应用的一项重要技术，且许多混沌系统可以转化为Lur’e系统，例如Chua’s电路、超混沌吸引子等。因此，Lur’e系统的同步研究引起了学者的广泛关注。

在实际工程中，非线性系统中时滞广泛存在，因此研究时滞不仅具有理论意义还具有实际意义。时滞的存在会影响系统的稳定性和性能，在使用采样反馈控制的混沌Lur’e系统同步问题中，已有文献考虑了常数时间延迟 [1] [2] [3] [4] [5]。史等处理在时滞系统中的时间延迟时应用时滞分割方法 [6]。为了减小时变时滞系统稳定性条件的保守性，人们提出了许多方法。主要的工作集中在两个方面：一是构造L-K泛函的技术，如时滞分割泛函，依赖于时间延迟的矩阵泛函 [7]，泛函包括具有三重积分项的函数 [8]，和二次项相乘的高次标量函数 [9]。另一种是估计L-K泛函时间导数的分析方法，如改进的优化技术、自由加权矩阵法 [10]，积分不等式包括Jensen不等式 [11]、Wirtinger不等式 [12]、基于辅助函数的积分不等式 [13]、逆凸矩阵不等式 [14]。

随着计算机技术、微电子技术、网络技术的迅速发展，在工业中数字设备已逐渐取代模拟设备，这使得控制系统只使用在离散时刻信号的采样值，极大减少了网络中信息量的传输。采样数据反馈控制也受到学者的青睐，被广泛应用于控制系统的研究之中。

为了进一步提高控制系统的宽带利用率，在系统中引入了事件触发机制，本文中的事件触发机制采用的是非周期采样控制策略，只有在满足事件触发条件的情况下，当前采样数据才会被传输到网络中，否则将保持上一次传输的数据。与传统的周期采样控制相比，在确保控制系统性能的前提下，引入事件触发机制能够减少不必要的数据传输到网络中，有效地提高网络通信带宽的利用率，降低网络拥塞的可能性。文献提出了基于事件触发机制量化数据采样控制器来实现混沌Lur’e系统主从同步 [15] [16]，是简单的周期性采样，且文章没有涉及到时滞和不确定性。文献 [16] 针对一类网络非线性互联系统的分散滤波问题，设计了一种自适应的事件触发方案 [17]。文献考虑了具有参数不确定的Lur’e系统时变时滞反馈控制 [18] [19]。

综上所述，本文提出了一种基于非周期事件触发的参数不确定的时滞混沌Lur’e系统采样数据主从同步方法。本文所提方法的主要创新点：1) 本文考虑了时变时滞的下界信息，而不是0。2) 所构造L-K函数，并不要求每一部分都是正定的，只要保证L-K函数整体的正定性，就能获得保守性更低的稳定性判据。3) 在稳定性分析和控制器综合中考虑了具有非周期事件触发机制的混沌Lur’e系统的主从同步问题，并将周期事件触发系统作为一个特例来考虑。4) 在估计L-K泛函导数中出现的积分时引用了基于辅助函数的积分不等式，基于辅助函数的积分不等式包含了Jensen不等式和Wirtinger积分不等式，对交叉积分项的放大程度更接近于真实值，所以泛函导数也更接近于真实值，因此本文能够得到的同步判据保守性更低。

2. 问题描述

参数不确定性时变时滞Lur’e系统主从同步模型如下：

$M:\{\begin{array}{c}\stackrel{\dot{}}{x}\left(t\right)=\left(A+\Delta {\rm A}\left(t\right)\right)x\left(t\right)+\left(B+\Delta B\left(t\right)\right)x\left(t-\tau \left(t\right)\right)+\left(E+\Delta E\left(t\right)\right)f\left(Dx\left(t\right)\right)\\ p\left(t\right)=Cx\left(t\right)\end{array}$ (1)

$S:\{\begin{array}{c}\stackrel{\dot{}}{y}\left(t\right)=\left(A+\Delta {\rm A}\left(t\right)\right)y\left(t\right)+\left(B+\Delta B\left(t\right)\right)y\left(t-\tau \left(t\right)\right)+\left(E+\Delta E\left(t\right)\right)f\left(Dy\left(t\right)\right)+U\left(t\right)\\ q\left(t\right)=Cy\left(t\right)\end{array}$ (2)

其中， $M$ 是主系统， $S$ 是主系统， $x\left(t\right)\in R^n,y\left(t\right)\in R^n$ 是主系统状态向量， $p\left(t\right)\in R^l,q\left(t\right)\in R^l$ 是输出向量， $A\in R^{n\times n},B\in R^{n\times n},C\in R^{l\times n},E\in R^{n\times m}$ 是已知矩阵，时变时滞 $\tau \left(t\right)$ 满足：

$0\le {\tau }_1\le \tau \left(t\right)\le {\tau }_2,u_1\le \stackrel{\dot{}}{\tau }\left(t\right)\le u_2$ (3)

非线性函数 $f(\cdot ):R^m\to R^m$ 属于扇区 $\left[k_i^{-},k_i^{+}\right]$，满足如下条件：

$k_i^{-}\le \frac{f_i\left(s_1\right)-f_i\left(s_2\right)}{s_1-s_2}\le k_i^{+},s_1\ne s_2,i=1,2,\cdots ,m$ (4)

假设参数不确定矩阵 $\Delta A,\Delta B,\Delta E$ 满足如下条件：

$\left[\Delta A\left(t\right),\Delta B\left(t\right),\Delta E\left(t\right)\right]=M\Delta \left(t\right)\left[N_1,N_2,N_3\right]$ (5)

其中， $M,N_1,N_2,N_3$ 是已知的具有适当维数的矩阵， $\Delta \left(t\right)$ 是连续时变非线性函数，满足：

${\Delta }^{\text{T}}\left(t\right)\Delta \left(t\right)\le I$ (6)

假设同步误差仅利用采样瞬间 $t_s$ 的数据，且 $0=t_0\cdots <t_s<\cdots +\infty$，采样周期 $h_s$ 并不是常数，满足：

$0\le r\left(t\right)=t-t_s\le h,\forall s\ge 0$ (7)

其中 $h_m,h_M$ 分别是采样周期的上界和下界。

实现混沌Lur’e系统主从同步的采样控制器如下：

$C:U\left(t\right)=K\left(p\left(t_k\right)-q\left(t_k\right)\right),t_k\le t<t_{k+1}$ (8)

其中， $K$ 是控制增益矩阵。

令 $e\left(t\right)=x\left(t\right)-y\left(t\right)$，由(1)、(2)、(8)可以获得同步误差系统：

$\begin{array}{l}\stackrel{\dot{}}{e}\left(t\right)=\left(A+\Delta A\left(t\right)\right)e\left(t\right)+\left(B+\Delta B\left(t\right)\right)e\left(t-\tau \left(t\right)\right)\\ +\left(E+\Delta E\left(t\right)\right)g\left(De\left(t\right)\right)-KCe\left(t_k\right),t_k\le t<t_{k+1}\end{array}$ (9)

其中， $g\left(De\left(t\right)\right)=f\left(De\left(t\right)+Dy\left(t\right)\right)-f\left(Dy\left(t\right)\right)$，从式(4)可以得到

$k_i^{-}\le \frac{g_i\left(d_i^{\text{T}}e,y\right)}{d_i^{\text{T}}e}=\frac{f_i\left(d_i^{\text{T}}\left(y+e\right)\right)-f_i\left(d_i^{\text{T}}y\right)}{d_i^{\text{T}}e}\le k_i^{+},d_i^{\text{T}}e\ne 0$ (10)

其中， $d_i^{\text{T}}$ 是矩阵D的第i行。

当前采样数据是否传输给控制器取决于事件触发条件，当前采样数据满足触发条件时，将会被传输到控制器，当前采样数据不满足触发条件时，将保持传感器的数据不变。本文所设计的事件触发条件如下：

${\epsilon }^{\text{T}}\left(t_s\right){\Theta }_1\epsilon \left(t_s\right)-{\sigma }_1(t)e^{\text{T}}\left(t_s\right){\Theta }_{2}e\left(t_s\right)-{\sigma }_2\left(t\right)e^{\text{T}}\left(t_k\right){\Theta }_{3}e\left(t_k\right)\le 0$ (11)

其中 $t_s=t_k+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{h}_i}$ 是当前采样时刻， $t_k$ 最近传输时刻， $\epsilon \left(t_s\right)=e\left(t_s\right)-e\left(t_k\right)$，矩阵 ${\Theta }_i\left(i=1,2,3\right)$ 是正定对称矩阵，函数 ${\sigma }_1\left(t\right),{\sigma }_2\left(t\right)$ 满足：

${\stackrel{\dot{}}{\sigma }}_1\left(t\right)=\frac{1}{{\sigma }_1\left(t\right)}\left[\frac{1}{{\sigma }_1\left(t\right)}-{\mu }_1\right]\left[{\epsilon }^{\text{T}}\left(t_s\right){\Theta }_1\epsilon \left(t_s\right)-{\kappa }_1{e}^{\text{T}}\left(t_k\right){\Theta }_{3}e\left(t_k\right)\right]$ (12)

${\stackrel{\dot{}}{\sigma }}_2\left(t\right)=\frac{1}{{\sigma }_2\left(t\right)}\left[\frac{1}{{\sigma }_2\left(t\right)}-{\mu }_2\right]\left[{\epsilon }^{\text{T}}\left(t_s\right){\Theta }_1\epsilon \left(t_s\right)-{\kappa }_2{e}^{\text{T}}\left(t_s\right){\Theta }_{2}e\left(t_s\right)\right]$ (13)

其中， ${\mu }_1,{\mu }_2,{\kappa }_1,{\kappa }_2$ 是给定的正常数，使得 $\frac{1}{{\mu }_1}<{\sigma }_1\left(t\right)<{\kappa }_2,\frac{1}{{\mu }_2}<{\sigma }_2\left(t\right)<{\kappa }_1$。

为了便于分析，保持区间H被分解成集合 $H_s=\left[t_s,t_{s+1}\right),H=\cup H_s,s=0,1\cdots ,t_{k+1}-t_k-1.$ 在这种情况下，同步误差系统(9)可以转化为

$\begin{array}{l}\stackrel{\dot{}}{e}\left(t\right)=\left(A+\Delta A\left(t\right)\right)e\left(t\right)+\left(B+\Delta B\left(t\right)\right)e\left(t-\tau \left(t\right)\right)\\ +\left(E+\Delta E\left(t\right)\right)g\left(De\left(t\right)\right)-KCe\left(t_s\right)+K\epsilon \left(t_s\right),t\in H_s\end{array}$ (14)

为了获得混沌Lur’e系统主从同步的判据，需要引入如下引理。

引理1 [20] 给定一个正定矩阵 $R>0$，对于连续函数 $\left\{\omega \left(s\right)|s\in \left[a,b\right]\right\}$，使如下不等式成立：

$\left(b-a\right){\displaystyle {\int }_a^b{\omega }^T\left(s\right)}R\omega \left(s\right)\text{d}s\ge {\left({\displaystyle {\int }_a^b\omega \left(s\right)}\text{d}s\right)}^{\text{T}}R\left({\displaystyle {\int }_a^b\omega \left(s\right)}\text{d}s\right)+3{\theta }^{\text{T}}R\theta$

其中， $\theta ={\displaystyle {\int }_a^b\omega \left(s\right)}\text{d}s-\frac{2}{b-a}{\displaystyle {\int }_a^b{\displaystyle {\int }_a^r\omega \left(s\right)}}\text{d}s\text{d}r$。

引理2 [13] 对于任意给定的正定矩阵 $R>0$，和一个可微函数 $\left\{x\left(u\right)|u\in \left[a,b\right]\right\}$，使如下不等式成立：

$\begin{array}{l}{\displaystyle {\int }_a^b{\stackrel{\dot{}}{x}}^T}\left(s\right)R\stackrel{\dot{}}{x}\left(s\right)\text{d}s\ge \frac{1}{b-a}{\Omega }_1^{T}R{\Omega }_1+\frac{3}{b-a}{\Omega }_2^{T}R{\Omega }_2+\frac{5}{b-a}{\Omega }_3^{T}R{\Omega }_3\\ {\displaystyle {\int }_a^b{\displaystyle {\int }_{\theta }^b{\stackrel{\dot{}}{x}}^T\left(s\right)}}R\stackrel{\dot{}}{x}\left(s\right)\text{d}s\text{d}\theta \ge 2{\Omega }_4^{T}R{\Omega }_4+4{\Omega }_5^{T}R{\Omega }_5\end{array}$

其中，

$\begin{array}{l}{\Omega }_1=x\left(b\right)-x\left(a\right),{\Omega }_2=x\left(b\right)+x\left(a\right)-\frac{1}{b-a}{\displaystyle {\int }_a^{b}x\left(s\right)}\text{d}s\\ {\Omega }_3={\Omega }_1+\frac{6}{b-a}{\displaystyle {\int }_a^{b}x\left(s\right)}\text{d}s-\frac{12}{{\left(b-a\right)}^2}{\displaystyle {\int }_a^b{\displaystyle {\int }_{\theta }^{b}x\left(s\right)\text{d}s\text{d}\theta }}\\ {\Omega }_4=x\left(b\right)-\frac{1}{b-a}{\displaystyle {\int }_a^{b}x\left(s\right)}\text{d}s,{\Omega }_5=x\left(b\right)+\frac{2}{b-a}{\displaystyle {\int }_a^{b}x\left(s\right)}\text{d}s-\frac{6}{{\left(b-a\right)}^2}{\displaystyle {\int }_a^b{\displaystyle {\int }_{\theta }^{b}x\left(s\right)\text{d}s\text{d}\theta }}\end{array}$

引理3 [14] 对于任意标量 $0<\alpha ,\beta <1$ 且 $\alpha +\beta =1$，如果存在矩阵 $R_1>0,R_2>0$，和任意适当维数矩阵 $S_1$ 和 $S_2$，使如下不等式成立：

$\left(\begin{array}{cc}\frac{1}{\alpha }{R}_1& \\ & \frac{1}{\beta }{R}_2\end{array}\right)\ge \left(\begin{array}{cc}{R}_1+\left(1-\alpha \right)P_1& \left(1-\alpha \right)S_1+\alpha S_2\\ \ast & R_2+\alpha P_2\end{array}\right)$

其中， $P_1=R_1-S_2{R}_2^{-1}{S}_2^{\text{T}},P_2=R_2-S_1^{\text{T}}{R}_1^{-1}{S}_1$。

引理4 [21] 给出适当维数的矩阵 $\Gamma ,\Xi ,\Psi$ 且 ${\Psi }^{\text{T}}=\Psi$，若对于任意矩阵 $F$ 满足 $F^{\text{T}}F\le I$，且满足不等式 $\Psi +\Gamma F\Xi +{\Xi }^{\text{T}}{F}^{\text{T}}{\Gamma }^{\text{T}}<0$，则存在一个实数 $\epsilon >0$，使如下不等式成立：

$\Psi +{\epsilon }^{-1}\Gamma {\Gamma }^{\text{T}}+\epsilon {\Xi }^{\text{T}}\Xi <0$

引理5 [8] 对于给定的对称矩阵 $S=\left(\begin{array}{cc}{S}_{11}& S_{12}\\ \ast & S_{22}\end{array}\right)$，下面三个条件等价

$\begin{array}{l}\text{1)}S<0;\\ 2)S_{11}<0,S_{22}-S_{12}^T{S}_{11}^{-1}{S}_{12}<0;\\ 3)S_{22}<0,S_{11}-S_{12}{S}_{22}^{-1}{S}_{12}^T<0;\end{array}$

引理6 [22] 假设 $\tau \left(t\right)\in \left[{\tau }_m,{\tau }_M\right],h\left(t\right)\in \left[0,h_M\right],$ 具有合适维数的矩阵 ${\Xi }_1,{\Xi }_2,{\Xi }_3,{\Xi }_4$ $\Omega$，使得如下不等式成立

$\Omega +\left(\tau \left(t\right)-{\tau }_m\right){\Xi }_1+\left({\tau }_M-\tau \left(t\right)\right){\Xi }_2+h\left(t\right){\Xi }_3+\left(h_M-h\left(t\right)\right){\Xi }_4<0$

当且仅当

$\begin{array}{l}\Omega +\left({\tau }_M-{\tau }_m\right){\Xi }_1+h_M{\Xi }_3<0\\ \Omega +\left({\tau }_M-{\tau }_m\right){\Xi }_2+h_M{\Xi }_3<0\\ \Omega +\left({\tau }_M-{\tau }_m\right){\Xi }_1+h_M{\Xi }_4<0\\ \Omega +\left({\tau }_M-{\tau }_m\right){\Xi }_2+h_M{\Xi }_4<0\end{array}$

为了简化文章的证明过程，首先给出相应的记号：

$\begin{array}{l}\xi \left(t\right)=col\{e\left(t\right),e\left(t-{\tau }_1\right),e\left(t-\tau \left(t\right)\right),e\left(t-{\tau }_2\right),e\left(t_s\right),g\left(De\left(t\right)\right),\frac{1}{{\tau }_1}{\displaystyle {\int }_{t-{\tau }_1}^{t}e\left(s\right)}\text{d}s,\frac{1}{\tau \left(t\right)-{\tau }_1}{\displaystyle {\int }_{t-\tau \left(t\right)}^{t-{\tau }_1}e\left(s\right)}\text{d}s,\\ \frac{1}{{\tau }_2-\tau \left(t\right)}{\displaystyle {\int }_{t-{\tau }_2}^{t-\tau \left(t\right)}e\left(s\right)}\text{d}s,\frac{1}{t-t_s}{\displaystyle {\int }_{t_s}^{t}e\left(s\right)}\text{d}s,\frac{2}{{\tau }_1^2}{\displaystyle {\int }_{t-{\tau }_1}^t{\displaystyle {\int }_{\theta }^{t}e\left(s\right)}}\text{d}s\text{d}\theta ,\frac{2}{{\left[\tau \left(t\right)-{\tau }_1\right]}^2}{\displaystyle {\int }_{t-\tau \left(t\right)}^{t-{\tau }_1}{\displaystyle {\int }_{\theta }^{t-{\tau }_1}e\left(s\right)}}\text{d}s\text{d}\theta ,\\ \frac{2}{{\left[{\tau }_2-\tau \left(t\right)\right]}^2}{\displaystyle {\int }_{t-{\tau }_2}^{t-\tau \left(t\right)}{\displaystyle {\int }_{\theta }^{t-\tau \left(t\right)}e\left(s\right)}}\text{d}s\text{d}\theta ,\frac{1}{{\left(t-t_s\right)}^2}{\displaystyle {\int }_{t_s}^t{\displaystyle {\int }_{\theta }^{t}e\left(s\right)}}\text{d}s\text{d}\theta ,\stackrel{\dot{}}{e}\left(t\right),\epsilon \left(t_s\right)\}\end{array}$

${\eta }_1\left(t\right)=col\left\{e\left(t\right),e\left(t_s\right),{\displaystyle {\int }_{t_s}^{t}e\left(s\right)\mathrm{d}s}\right\}$

$X=\left(\begin{array}{ccc}\frac{X_1^{\text{T}}+X_1-X_2^{\text{T}}-X_2}{2}& X_2& X_3\\ \ast & \frac{-X_1^{\text{T}}-X_1-X_2^{\text{T}}-X_2}{2}& X_4\\ \ast & \ast & X_5^{\text{T}}+X_5\end{array}\right)$

$\begin{array}{l}L=col\left\{G^{\text{T}}000G^{\text{T}}000000000G^{\text{T}}0\right\}\\ N=\left\{N_{1}0N_{2}00N_{3}0000000000\right\}\end{array}$

$e_i=\left(\begin{array}{ccc}{0}_{n\times \left(i-1\right)n}& I_n& 0_{n\times \left[\left(15-i\right)n+m\right]}\end{array}\right),i=1,2,\cdots ,5e_6=\left(\begin{array}{ccc}{0}_{m\times 5n}& I_m& 0_{m\times 10n}\end{array}\right)$

$e_i=\left(\begin{array}{ccc}{0}_{n\times \left[\left(i-2\right)n+m\right]}& I_n& 0_{n\times \left(16-i\right)n}\end{array}\right),i=7,8,\cdots ,16$

$E_1=\left(\begin{array}{c}{e}_2-e_3\\ e_2+e_3-2e_8\\ e_2-e_3+6e_8-6e_{12}\end{array}\right),E_2=\left(\begin{array}{c}{e}_3-e_4\\ e_3+e_4-2e_9\\ e_3-e_4+6e_9-6e_{13}\end{array}\right)$

3. 主要结果

在这一部分中，给出使参数不确定时滞混沌Lur’e系统基于事件触发机制的采样控制器设计实现主从同步的方法，建立闭环系统(14)收敛的充分条件。

定理1：对于给定的标量 $h>0,{\tau }_2\ge {\tau }_1\ge 0,{\mu }_i>0,{\kappa }_i>0\left(i=1,2\right)$，如果存在适当维数的矩阵 $P>0,$ $Q>0,R_i>0\left(i=1,2,3\right),$ $J_i>0\left(i=1,2,\cdots ,6\right),$ ${\Theta }_i>0\left(i=1,2,3\right),$ ${\bar{J}}_i=diag\left(J_i,3J_i,5J_i\right)\left(i=4,6\right)$，任意适当维数矩阵 $X,P_i\left(i=1,2\right)$ 和G，使得下列LMIs是可行的：

$\left(\begin{array}{ccc}P+\frac{h\left(X_1^{\text{T}}+X_1-X_2^{\text{T}}-X_2\right)}{2}& h{X}_2& h{X}_3\\ \ast & \frac{-h\left(X_1^{\text{T}}+X_1+X_2^{\text{T}}+X_2\right)}{2}& h{X}_4\\ \ast & \ast & h\left(X_5^{\text{T}}+X_5\right)\end{array}\right)>0$ (15)

$\left(\begin{array}{cccc}{\Psi }_1+{\Psi }_i+{\Psi }_{4,1}& P_2& LM& \epsilon N^{\text{T}}\\ \ast & {\bar{J}}_4& 0& 0\\ \ast & \ast & -\epsilon I& 0\\ \ast & \ast & \ast & -\epsilon I\end{array}\right)<0$ (16)

$\left(\begin{array}{cccc}{\Psi }_1+{\Psi }_i+{\Psi }_{4,2}& P_1^{\text{T}}& LM& \epsilon N^{\text{T}}\\ \ast & {\bar{J}}_4+{\bar{J}}_6& 0& 0\\ \ast & \ast & -\epsilon I& 0\\ \ast & \ast & \ast & -\epsilon I\end{array}\right)<0$ (17)

0元素除外， ${\Psi }_1={\left[{\Psi }_{ij}\right]}_{16\times 16}$ 的剩余元素如下：

${\Psi }_{11}=Sym\left\{\left(X_2-X_1\right)/2-D^{\text{T}}{K}_2^{\text{T}}F{K}_{1}D+GA\right\}-6R_3-\left({\text{π}}^2/4\right)Q+J_1-9J_3-6J_5,{\Psi }_{12}=3J_3,{\Psi }_{13}=GB,$

${\Psi }_{15}=-X_2+\frac{{\text{π}}^2}{4}Q+A^{\text{T}}{G}^{\text{T}}-YC,{\Psi }_{16}=GE+D^{\text{T}}{K}_1^{\text{T}}{F}^{\text{T}}+D^{\text{T}}{K}_2^{\text{T}}F,{\Psi }_{17}=-24J_3-6J_5,$

${\Psi }_{1,10}=\left(h^2/4\right)Sym\left\{X_5\right\}-R_{22}-6R_3,{\Psi }_{1,11}=30J_3+12J_5,{\Psi }_{1,14}=12R_3,$

${\Psi }_{1,15}=P+D^{\text{T}}{K}_2\Lambda D-D^{\text{T}}{K}_1\Delta D-G+A^{\text{T}}{G}^{\text{T}},{\Psi }_{1,16}=YC,{\Psi }_{2,2}=-J_1+J_2-9J_3-6J_6,$

${\Psi }_{2,7}=30J_3,{\Psi }_{2,8}=-6J_6,{\Psi }_{2,11}=-30J_3,{\Psi }_{2,12}=12J_6,{\Psi }_{3,3}=-6J_6,{\Psi }_{3,5}=B^T{G}^T,{\Psi }_{3,9}=-6J_6,{\Psi }_{3,13}=12J_6,$

${\Psi }_{3,15}=B^{\text{T}}{G}^{\text{T}},{\Psi }_{4,4}=-J_2,{\Psi }_{5,5}=-Sym\left\{YC-\frac{X_1+X_2}{2}\right\}-\frac{{\text{π}}^2}{4}Q+\left(1+u_2{k}_2\right){\Theta }_2+\left(1+u_1{k}_1\right){\Theta }_3,{\Psi }_{5,6}=GE,$

${\Psi }_{5,15}=-G-C^{\text{T}}{Y}^{\text{T}},{\Psi }_{5,16}=-\left(1+u_1{k}_1\right){\Theta }_3+YC,{\Psi }_{6,6}=-Sym\left\{F\right\},{\Psi }_{6,15}=-\Lambda D+\Delta D+E^{\text{T}}{G}^{\text{T}},$

${\Psi }_{7,7}=-192J_3-18J_5,{\Psi }_{7,11}=180J_3+24J_5,{\Psi }_{8,8}=-18J_6,{\Psi }_{8,12}=24J_6,{\Psi }_{9,9}=-18J_6,{\Psi }_{9,13}=24J_6,$

${\Psi }_{10,10}=-18R_3,{\Psi }_{10,14}=24R_3,{\Psi }_{10,15}=\frac{h^2}{4}{X}_3^{\text{T}},{\Psi }_{11,11}=-180J_3-36J_5,{\Psi }_{12,12}=-36J_6,$

${\Psi }_{13,13}=-36J_6,{\Psi }_{14,14}=-36R_3,{\Psi }_{15,15}=h^{2}Q+\frac{h^2}{4}{R}_3+{\tau }_1^2{J}_3+{\left({\tau }_2-{\tau }_1\right)}^2{J}_4+\frac{{\tau }_1^2}{2}{J}_5+\frac{{\tau }_2^2-{\tau }_1^2}{2}{J}_6-Sym\left\{G\right\},$

${\Psi }_{15,16}=YC,{\Psi }_{16,16}=\left(1+{\mu }_1{k}_1\right){\Theta }_3-\left({\mu }_1+{\mu }_2\right){\Theta }_1$

$\begin{array}{l}{\Psi }_2={\Psi }_1+e_1^{\text{T}}h\left(R_1+R_{21}+Sym\left\{X_3\right\}\right)e_1+e_1^{\text{T}}h\left(X_4^{\text{T}}+R_{22}\right)e_5+e_1^{\text{T}}Sym\left\{h\left(X_1-X_2\right)/2\right\}{e}_{15}+e_5^{\text{T}}h{R}_{23}{e}_5\\ +e_5^{T}h{X}_2^{\text{T}}{e}_{15}+e_{15}^{\text{T}}h{R}_2{e}_{15}\end{array}$

${\Psi }_3={\Psi }_1-e_1^{\text{T}}h{X}_3{e}_{10}-e_5^{\text{T}}h{R}_{23}{e}_5-e_5^{\text{T}}h{X}_4{e}_{10}-4h{e}_{10}^{\text{T}}\left(R_1+R_{21}\right)e_{10}-e_{10}^{\text{T}}Sym\left\{h^2{X}_5\right\}{e}_{10}-3h{e}_{14}^{\text{T}}\left(R_1+R_{21}\right)e_{14}$

$\begin{array}{l}{\Psi }_4\left(\tau \left(t\right)\right)=-\left[E_1^{\text{T}}\left({\bar{J}}_4+{\bar{J}}_6\right)E_1+E_2^{\text{T}}{\bar{J}}_4{E}_2-E_1^{\text{T}}{\bar{J}}_6{E}_1\right]\\ -\frac{{\tau }_2-\tau \left(t\right)}{{\tau }_2-{\tau }_1}{\left(\begin{array}{c}{E}_1\\ E_2\end{array}\right)}^{\text{T}}\left(\begin{array}{cc}{\bar{J}}_4+{\bar{J}}_6-P_2{\bar{J}}_4^{-1}{P}_2{}^{\mathrm{T}}& P_1\\ \ast & 0\end{array}\right)\left(\begin{array}{c}{E}_1\\ E_2\end{array}\right)\\ -\frac{\tau \left(t\right)-{\tau }_1}{{\tau }_2-{\tau }_1}{\left(\begin{array}{c}{E}_1\\ E_2\end{array}\right)}^{\text{T}}\left(\begin{array}{cc}0& P_2\\ \ast & {\bar{J}}_4-P_1^T{\left({\bar{J}}_4+{\bar{J}}_6\right)}^{-1}{P}_1\end{array}\right)\left(\begin{array}{c}{E}_1\\ E_2\end{array}\right)\end{array}$

${\Psi }_{4,1}={\left(\begin{array}{c}{E}_1\\ E_2\end{array}\right)}^{\text{T}}\left(\begin{array}{cc}2{\bar{J}}_4+{\bar{J}}_6& P_1\\ \ast & {\bar{J}}_4\end{array}\right)\left(\begin{array}{c}{E}_1\\ E_2\end{array}\right),{\Psi }_{4,2}={\left(\begin{array}{c}{E}_1\\ E_2\end{array}\right)}^{\text{T}}\left(\begin{array}{cc}{\bar{J}}_4& P_2\\ \ast & 2{\bar{J}}_4{}_1\end{array}\right)\left(\begin{array}{c}{E}_1\\ E_2\end{array}\right)$

则误差系统(14)是全局渐近稳定。且时滞反馈控制增益矩阵为：

$K=G^{-1}Y$

证明：构造的Lyapunov-Krasovskii泛函如下：

$V\left(t\right)={\displaystyle \underset{i=1}{\overset{7}{\sum }}{V}_i}\left(t\right)$ (18)

$V_1\left(t\right)=e^{\text{T}}(t)Pe(t)+\left(h-r\left(t\right)\right){\eta }_1^{\text{T}}\left(t\right)X{\eta }_1(\; t\; )$

$V_2\left(t\right)=2{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\displaystyle {\int }_0^{d_i^{\text{T}}e}{\lambda }_i}}\left[k_i^{+}s-g_i\left(s\right)\right]\text{d}s+2{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\displaystyle {\int }_0^{d_i^{\text{T}}Z(t)}{\delta }_i}}\left[g_i\left(s\right)-k_i^{-}s\right]\text{d}s$

$V_3\left(t\right)=\left(h-r\left(t\right)\right){\displaystyle {\int }_{t_s}^t{e}^{\text{T}}}\left(s\right)R_{1}e\left(s\right)\text{d}s+\left(h-r\left(t\right)\right){\displaystyle {\int }_{t_s}^t\left[e^{\text{T}}\left(s\right)e^{\text{T}}\left(t_s\right)\right]}{R}_2{\left[e^{\text{T}}\left(s\right)e^{\text{T}}\left(t_s\right)\right]}^T\text{d}s$

$V_4\left(t\right)=\left(h-r\left(t\right)\right){\displaystyle {\int }_{t_s}^t{\displaystyle {\int }_{\theta }^t{\stackrel{\dot{}}{e}}^{\text{T}}}\left(s\right)R_3\stackrel{\dot{}}{e}\left(s\right)\text{d}s}\text{d}\theta$

$V_5\left(t\right)=h^2{\displaystyle {\int }_{t_s}^t{\stackrel{\dot{}}{e}}^{\text{T}}}\left(s\right)Q\stackrel{\dot{}}{e}\left(S\right)\text{d}s-\frac{{\text{π}}^2}{4}{\displaystyle {\int }_{t_s}^t{\left[e\left(t\right)-e\left(t_s\right)\right]}^{\text{T}}Q\left[e\left(t\right)-e\left(t_s\right)\right]\text{d}s}$

$\begin{array}{l}{V}_6\left(t\right)={\displaystyle {\int }_{t-{\tau }_1}^t{e}^{\text{T}}\left(s\right)}{J}_{1}e\left(s\right)\text{d}s+{\displaystyle {\int }_{t-{\tau }_2}^{t-{\tau }_1}{e}^{\text{T}}\left(s\right)}{J}_{2}e\left(s\right)\text{d}s\\ +{\tau }_1{\displaystyle {\int }_{t-{\tau }_1}^t{\displaystyle {\int }_{\theta }^t{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)}}{J}_3\stackrel{\dot{}}{e}\left(s\right)\text{d}s\text{d}\theta +\left({\tau }_2-{\tau }_1\right){\displaystyle {\int }_{t-{\tau }_2}^{t-{\tau }_1}{\displaystyle {\int }_{\theta }^t{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)}}{J}_4\stackrel{\dot{}}{e}\left(s\right)\text{d}s\text{d}\theta \\ +{\displaystyle {\int }_{t-{\tau }_1}^t{\displaystyle {\int }_{\rho }^t{\displaystyle {\int }_{\theta }^t{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)}}}{J}_5\stackrel{\dot{}}{e}\left(s\right)\text{d}s\text{d}\theta \text{d}\rho +{\displaystyle {\int }_{t-{\tau }_2}^{t-{\tau }_1}{\displaystyle {\int }_{\rho }^{t-{\tau }_1}{\displaystyle {\int }_{\theta }^t{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)}}}{J}_6\stackrel{\dot{}}{e}\left(s\right)\text{d}s\text{d}\theta \text{d}\rho \end{array}$

$V_7\left(t\right)=\frac{1}{2}{\sigma }_1^2\left(t\right)+\frac{1}{2}{\sigma }_2^2(\; t\; )$

沿着误差系统(14)的轨线，求 $V\left(t\right)$ 关于时间的导数：

${\stackrel{\dot{}}{V}}_1\left(t\right)=2e^{\text{T}}\left(t\right)P\stackrel{\dot{}}{e}\left(t\right)-{\eta }_1^{\text{T}}\left(t\right)X{\eta }_1\left(t\right)+2\left(h-r\left(t\right)\right){\eta }_1^{\text{T}}\left(t\right)X{\stackrel{\dot{}}{\eta }}_1\left(t\right)$ (19)

${\stackrel{\dot{}}{V}}_2\left(t\right)=2\left[\left(e^{\text{T}}\left(t\right)D^{\text{T}}{K}_2-g^{\text{T}}\left(D^{\text{T}}e\left(t\right)\right)\right)\Lambda D\stackrel{\dot{}}{e}\left(t\right)+\left(g^{\text{T}}\left(D^{\text{T}}e\left(t\right)\right)-e^{\text{T}}\left(t\right)D^{\text{T}}{K}_1\right)\Delta D\stackrel{\dot{}}{e}\left(t\right)\right]$ (20)

$\begin{array}{c}{\stackrel{\dot{}}{V}}_3\left(t\right)=\left(h-r\left(t\right)\right)e^{\text{T}}\left(t\right)R_{1}e\left(t\right)-{\displaystyle {\int }_{t_s}^t{e}^{\text{T}}}\left(s\right)R_{1}e\left(s\right)\text{d}s\\ -{\displaystyle {\int }_{t_s}^t\left[e^{\text{T}}\left(s\right)e^{\text{T}}\left(t_s\right)\right]}{R}_2{\left[e^{\text{T}}\left(s\right)e^{\text{T}}\left(t_s\right)\right]}^{\text{T}}\text{d}s\\ +\left(h-r\left(t\right)\right)\left[e^{\text{T}}\left(t\right)e^{\text{T}}\left(t_s\right)\right]R_2{\left[e^{\text{T}}\left(t\right)e^{\text{T}}\left(t_s\right)\right]}^{\text{T}}\end{array}$ (21)

$\begin{array}{c}=\left(h-r\left(t\right)\right)e^T\left(t\right)R_{1}e\left(t\right)-{\displaystyle {\int }_{t_s}^t{e}^T}\left(s\right)R_{1}e\left(s\right)\text{d}s-{\displaystyle {\int }_{t_s}^t{e}^{\text{T}}\left(s\right)}{R}_{21}e\left(s\right)\text{d}s\\ -2{\displaystyle {\int }_{t_s}^t{e}^{\text{T}}\left(s\right)}\text{d}s{R}_{22}e\left(t_s\right)-r\left(t\right)e^{\text{T}}\left(t_s\right)R_{23}e\left(t_s\right)\\ +\left(h-r\left(t\right)\right)\left[e^{\text{T}}\left(t\right)R_{21}e\left(t\right)+2e^{\text{T}}\left(t\right)R_{22}e\left(t_s\right)+e^{\text{T}}\left(t_s\right)R_{23}e\left(t_s\right)\right]\end{array}$

$\begin{array}{l}{\stackrel{\dot{}}{V}}_4\left(t\right)=\left(h-r\left(t\right)\right)r\left(t\right){\stackrel{\dot{}}{e}}^{\text{T}}\left(t\right)R_3\stackrel{\dot{}}{e}\left(t\right)-{\displaystyle {\int }_{t_s}^t{\displaystyle {\int }_{\theta }^t{\stackrel{\dot{}}{e}}^{\text{T}}}\left(s\right)R_3\stackrel{\dot{}}{e}\left(s\right)\text{d}s}\text{d}\theta \\ \le \frac{h^2}{4}{\stackrel{\dot{}}{e}}^{\text{T}}\left(t\right)R_3\stackrel{\dot{}}{e}\left(t\right)-{\displaystyle {\int }_{t_s}^t{\displaystyle {\int }_{\theta }^t{\stackrel{\dot{}}{e}}^{\text{T}}}\left(s\right)R_3\stackrel{\dot{}}{e}\left(s\right)\text{d}s}\text{d}\theta \end{array}$ (22)

${\stackrel{\dot{}}{V}}_5\left(t\right)=h^2{\stackrel{\dot{}}{e}}^{\text{T}}\left(t\right)Q{\stackrel{\dot{}}{e}}^{\text{T}}\left(t\right)-\frac{{\text{π}}^2}{4}{\left[e\left(t\right)-e\left(t_s\right)\right]}^{\text{T}}Q\left[e\left(t\right)-e\left(t_s\right)\right]$ (23)

$\begin{array}{l}{\stackrel{\dot{}}{V}}_6\left(t\right)=e^{\text{T}}\left(t\right)J_{1}e\left(t\right)-e^{\text{T}}\left(t-{\tau }_1\right)J_{1}e\left(t-{\tau }_1\right)+e^{\text{T}}\left(t-{\tau }_1\right)J_{2}e\left(t-{\tau }_1\right)-e^{\text{T}}\left(t-{\tau }_2\right)J_{2}e\left(t-{\tau }_2\right)\\ +{\tau }_1^2{\stackrel{\dot{}}{e}}^{\text{T}}\left(t\right)J_3\stackrel{\dot{}}{e}\left(t\right)-{\tau }_1{\displaystyle {\int }_{t-{\tau }_1}^t{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)}{J}_3\stackrel{\dot{}}{e}\left(s\right)\text{d}s+{\left({\tau }_2-{\tau }_1\right)}^2{\stackrel{\dot{}}{e}}^{\text{T}}\left(t\right)J_4\stackrel{\dot{}}{e}\left(t\right)\\ -\left({\tau }_2-{\tau }_1\right){\displaystyle {\int }_{t-{\tau }_2}^{t-{\tau }_1}{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)}{J}_4\stackrel{\dot{}}{e}\left(s\right)\text{d}s+\frac{{\tau }_1^2}{2}{\stackrel{\dot{}}{e}}^{\text{T}}\left(t\right)J_5\stackrel{\dot{}}{e}\left(t\right)-{\displaystyle {\int }_{t-{\tau }_1}^t{\displaystyle {\int }_{\theta }^t{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)}}{J}_5\stackrel{\dot{}}{e}\left(s\right)\text{d}s\text{d}\theta \\ +\frac{{\tau }_2^2-{\tau }_1^2}{2}{\stackrel{\dot{}}{e}}^{\text{T}}\left(t\right)J_6\stackrel{\dot{}}{e}\left(t\right)-{\displaystyle {\int }_{t-{\tau }_2}^{t-{\tau }_1}{\displaystyle {\int }_{\theta }^{t-{\tau }_1}{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)J_6\stackrel{\dot{}}{e}\left(s\right)}}\text{d}s\text{d}\theta \end{array}$ (24)

$\begin{array}{l}{\stackrel{\dot{}}{V}}_7\left(t\right)={\sigma }_1\left(t\right){\stackrel{\dot{}}{\sigma }}_1\left(t\right)+{\sigma }_2\left(t\right){\stackrel{\dot{}}{\sigma }}_2\left(t\right)\\ =\left[\frac{1}{{\sigma }_1\left(t\right)}-{\mu }_1\right]\left[{\epsilon }^{\mathrm{T}}\left(t_s\right){\Theta }_1\epsilon \left(t_s\right)-{\kappa }_1{e}^{\mathrm{T}}\left(t_k\right){\Theta }_{3}e\left(t_k\right)\right]\\ +\left[\frac{1}{{\sigma }_2\left(t\right)}-{\mu }_2\right]\left[{\epsilon }^{\mathrm{T}}\left(t_s\right){\Theta }_1\epsilon \left(t_s\right)-{\kappa }_2{e}^{\mathrm{T}}\left(t_s\right){\Theta }_{2}e\left(t_s\right)\right]\end{array}$ (25)

$\begin{array}{l}\le e^{\text{T}}\left(t_s\right){\Theta }_{2}e\left(t_s\right)+\frac{{\sigma }_2\left(t\right)-{\kappa }_1}{{\sigma }_1\left(t\right)}{e}^{\mathrm{T}}\left(t_k\right){\Theta }_{3}e\left(t_k\right)-{\mu }_1\left[{\epsilon }^{\mathrm{T}}\left(t_s\right){\Theta }_1\epsilon \left(t_s\right)-{\kappa }_1{e}^{\mathrm{T}}\left(t_k\right){\Theta }_{3}e\left(t_k\right)\right]\\ +e^{\text{T}}\left(t_k\right){\Theta }_{3}e\left(t_k\right)+\frac{{\sigma }_1\left(t\right)-{\kappa }_2}{{\sigma }_2\left(t\right)}{e}^{\mathrm{T}}\left(t_s\right){\Theta }_{2}e\left(t_s\right)-{\mu }_2\left[{\epsilon }^{\mathrm{T}}\left(t_s\right){\Theta }_1\epsilon \left(t_s\right)-{\kappa }_2{e}^{\mathrm{T}}\left(t_s\right){\Theta }_{2}e\left(t_s\right)\right]\\ \le \left(1+{\mu }_2{\kappa }_2\right)e^{\mathrm{T}}\left(t_s\right){\Theta }_{2}e\left(t_s\right)+\left(1+{\mu }_1{\kappa }_1\right)e^{\mathrm{T}}\left(t_k\right){\Theta }_{3}e\left(t_k\right)-\left({\mu }_1+{\mu }_2\right){\epsilon }^{\mathrm{T}}\left(t_s\right){\Theta }_1\epsilon (\; t\; s\; )\end{array}$

根据引理1可得

$\begin{array}{l}-{\displaystyle {\int }_{t_s}^t{e}^{\text{T}}}\left(s\right)R_{1}e\left(s\right)\text{d}s\\ \le -\frac{1}{t-t_s}{\displaystyle {\int }_{t_s}^t{e}^{\text{T}}}\left(s\right)\text{d}s{R}_1{\displaystyle {\int }_{t_s}^{t}e\left(s\right)}\text{d}s\\ -\frac{3}{t-t_s}\left[{\displaystyle {\int }_{t_s}^t{e}^{\text{T}}\left(s\right)\text{d}s-\frac{2}{t-t_s}{\displaystyle {\int }_{t-t_s}^t{\displaystyle {\int }_{\theta }^t{e}^{\text{T}}}\left(s\right)\text{d}s\text{d}\theta }}\right]R_1\left[{\displaystyle {\int }_{t_s}^{t}e\left(s\right)\text{d}s-\frac{2}{t-t_s}{\displaystyle {\int }_{t-t_s}^t{\displaystyle {\int }_{\theta }^{t}e}\left(s\right)\text{d}s\text{d}\theta }}\right]\end{array}$ (26)

$\begin{array}{l}-{\displaystyle {\int }_{t_s}^t{e}^{\text{T}}\left(s\right)}{R}_{21}e\left(s\right)\text{d}s\\ \le -\frac{1}{t-t_s}{\displaystyle {\int }_{t_s}^t{e}^{\text{T}}}\left(s\right)\text{d}s{R}_{21}{\displaystyle {\int }_{t_s}^{t}e\left(s\right)}\text{d}s\\ -\frac{3}{t-t_s}\left[{\displaystyle {\int }_{t_s}^t{e}^{\text{T}}\left(s\right)\text{d}s-\frac{2}{t-t_s}{\displaystyle {\int }_{t-t_s}^t{\displaystyle {\int }_{\theta }^t{e}^{\text{T}}}\left(s\right)\text{d}s\text{d}\theta }}\right]R_{21}\left[{\displaystyle {\int }_{t_s}^{t}e\left(s\right)\text{d}s-\frac{2}{t-t_s}{\displaystyle {\int }_{t-t_s}^t{\displaystyle {\int }_{\theta }^{t}e}\left(s\right)\text{d}s\text{d}\theta }}\right]\end{array}$ (27)

根据引理2得

$\begin{array}{l}-{\displaystyle {\int }_{t-{\tau }_1}^t{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)}{J}_3\stackrel{\dot{}}{e}\left(s\right)\text{d}s\\ \le -\frac{1}{{\tau }_1}{\left[e\left(t\right)-e\left(t-t_1\right)\right]}^{\text{T}}{J}_3\left[e\left(t\right)-e\left(t-t_1\right)\right]\\ -\frac{3}{{\tau }_1}{\left[e\left(t\right)+e\left(t-t_1\right)-\frac{2}{{\tau }_1}{\displaystyle {\int }_{t-{\tau }_1}^{t}e\left(s\right)\text{d}s}\right]}^{\text{T}}{J}_3\left[e\left(t\right)+e\left(t-t_1\right)-\frac{2}{{\tau }_1}{\displaystyle {\int }_{t-{\tau }_1}^{t}e\left(s\right)\text{d}s}\right]\\ -\frac{5}{{\tau }_1}{\left[e\left(t\right)-e\left(t-t_1\right)+\frac{6}{{\tau }_1}{\displaystyle {\int }_{t-{\tau }_1}^{t}e\left(s\right)\text{d}s-\frac{12}{{\tau }_1{}^2}{\displaystyle {\int }_{t-{\tau }_1}^t{\displaystyle {\int }_{\theta }^{t}e\left(s\right)\text{d}s\text{d}\theta }}}\right]}^{\text{T}}{J}_3\\ \text{}\left[e\left(t\right)-e\left(t-t_1\right)+\frac{6}{{\tau }_1}{\displaystyle {\int }_{t-{\tau }_1}^{t}e\left(s\right)\text{d}s-\frac{12}{{\tau }_1{}^2}{\displaystyle {\int }_{t-{\tau }_1}^t{\displaystyle {\int }_{\theta }^{t}e\left(s\right)\text{d}s\text{d}\theta }}}\right]\end{array}$ (28)

$\begin{array}{l}-{\displaystyle {\int }_{t_s}^t{\displaystyle {\int }_{\theta }^t{\stackrel{\dot{}}{e}}^{\text{T}}}\left(s\right)R_3\stackrel{\dot{}}{e}\left(s\right)\text{d}s}\text{d}\theta \\ \le -2{\left[e\left(t\right)-\frac{1}{t-t_s}{\displaystyle {\int }_{t_s}^{t}e\left(s\right)\text{d}s}\right]}^{\text{T}}{R}_3\left[e\left(t\right)-\frac{1}{t-t_s}{\displaystyle {\int }_{t_s}^{t}e\left(s\right)\text{d}s}\right]\\ -4{\left[e\left(t\right)+\frac{2}{t-t_s}{\displaystyle {\int }_{t_s}^{t}e\left(s\right)\text{d}s-\frac{6}{{\left(t-t_s\right)}^2}{\displaystyle {\int }_{t_s}^t{\displaystyle {\int }_{\theta }^{t}e\left(s\right)\text{d}s\text{d}\theta }}}\right]}^{\text{T}}{R}_3\\ \left[e\left(t\right)+\frac{2}{t-t_s}{\displaystyle {\int }_{t_s}^{t}e\left(s\right)\text{d}s-\frac{6}{{\left(t-t_s\right)}^2}{\displaystyle {\int }_{t_s}^t{\displaystyle {\int }_{\theta }^{t}e\left(s\right)\text{d}s\text{d}\theta }}}\right]\end{array}$ (29)

$\begin{array}{l}-{\displaystyle {\int }_{t-{\tau }_1}^t{\displaystyle {\int }_{\theta }^t{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)}}{J}_5\stackrel{\dot{}}{e}\left(s\right)\text{d}s\text{d}\theta \\ \le -2{\left[e\left(t\right)-\frac{1}{{\tau }_1}{\displaystyle {\int }_{t-{\tau }_1}^{t}e\left(s\right)\text{d}s}\right]}^{\text{T}}{J}_5\left[e\left(t\right)-\frac{1}{{\tau }_1}{\displaystyle {\int }_{t-{\tau }_1}^{t}e\left(s\right)\text{d}s}\right]\\ -4{\left[e\left(t\right)+\frac{2}{{\tau }_1}{\displaystyle {\int }_{t-{\tau }_1}^{t}e\left(s\right)\text{d}s}-\frac{6}{{\tau }_1^2}{\displaystyle {\int }_{t-{\tau }_1}^t{\displaystyle {\int }_{\theta }^{t}e\left(s\right)}}\text{d}s\text{d}\theta \right]}^{\text{T}}{J}_5\\ \left[e\left(t\right)+\frac{2}{{\tau }_1}{\displaystyle {\int }_{t-{\tau }_1}^{t}e\left(s\right)\text{d}s}-\frac{6}{{\tau }_1^2}{\displaystyle {\int }_{t-{\tau }_1}^t{\displaystyle {\int }_s^{t}e\left(s\right)}}\text{d}s\text{d}\theta \right]\end{array}$ (30)

$\begin{array}{l}-{\displaystyle {\int }_{t-{\tau }_2}^{t-{\tau }_1}{\displaystyle {\int }_{\theta }^{t-{\tau }_1}{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)J_6\stackrel{\dot{}}{e}\left(s\right)}}\text{d}s\text{d}\theta =-\left({\displaystyle {\int }_{t-\tau \left(t\right)}^{t-{\tau }_1}{\displaystyle {\int }_{\theta }^{t-{\tau }_1}+{\displaystyle {\int }_{t-{\tau }_2}^{t-\tau \left(t\right)}{\displaystyle {\int }_{\theta }^{t-\tau \left(t\right)}+{\displaystyle {\int }_{t-{\tau }_2}^{t-\tau \left(t\right)}{\displaystyle {\int }_{t-\tau \left(t\right)}^{t-{\tau }_1}}}}}}}\right){\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)J_6\stackrel{\dot{}}{e}\left(s\right)\text{d}s\text{d}\theta \\ \le -2{\left[e\left(t-{\tau }_1\right)-\frac{1}{\tau \left(t\right)-{\tau }_1}{\displaystyle {\int }_{t-\tau \left(t\right)}^{t-{\tau }_1}e\left(s\right)}\text{d}s\right]}^{\text{T}}{J}_6\left[e\left(t-{\tau }_1\right)-\frac{1}{\tau \left(t\right)-{\tau }_1}{\displaystyle {\int }_{t-\tau \left(t\right)}^{t-{\tau }_1}e\left(s\right)}\text{d}s\right]\\ -4{\left[e\left(t-{\tau }_1\right)+\frac{2}{\tau \left(t\right)-{\tau }_1}{\displaystyle {\int }_{t-\tau \left(t\right)}^{t-{\tau }_1}e\left(s\right)}\text{d}s-\frac{6}{{\left[\tau \left(t\right)-{\tau }_1\right]}^2}{\displaystyle {\int }_{t-\tau \left(t\right)}^{t-{\tau }_1}{\displaystyle {\int }_{\theta }^{t-{\tau }_1}e\left(s\right)}}\text{d}s\text{d}\theta \right]}^{\text{T}}{J}_6\\ \left[e\left(t-{\tau }_1\right)+\frac{2}{\tau \left(t\right)-{\tau }_1}{\displaystyle {\int }_{t-\tau \left(t\right)}^{t-{\tau }_1}e\left(s\right)}\text{d}s-\frac{6}{{\left[\tau \left(t\right)-{\tau }_1\right]}^2}{\displaystyle {\int }_{t-\tau \left(t\right)}^{t-{\tau }_1}{\displaystyle {\int }_{\theta }^{t-{\tau }_1}e\left(s\right)}}\text{d}s\text{d}\theta \right]\end{array}$

$\begin{array}{l}-2{\left[e\left(t-\tau \left(t\right)\right)-\frac{1}{{\tau }_2-\tau \left(t\right)}{\displaystyle {\int }_{t-{\tau }_2}^{t-\tau \left(t\right)}e\left(s\right)}\text{d}s\right]}^{\text{T}}{J}_6\left[e\left(t-\tau \left(t\right)\right)-\frac{1}{{\tau }_2-\tau \left(t\right)}{\displaystyle {\int }_{t-{\tau }_2}^{t-\tau \left(t\right)}e\left(s\right)}\text{d}s\right]\\ -4{\left[e\left(t-\tau \left(t\right)\right)+\frac{2}{{\tau }_2-\tau \left(t\right)}{\displaystyle {\int }_{t-{\tau }_2}^{t-\tau \left(t\right)}e\left(s\right)}\text{d}s-\frac{6}{{\left[{\tau }_2-\tau \left(t\right)\right]}^2}{\displaystyle {\int }_{t-{\tau }_2}^{t-\tau \left(t\right)}{\displaystyle {\int }_{\theta }^{t-\tau \left(t\right)}e\left(s\right)}}\text{d}s\text{d}\theta \right]}^{\text{T}}{J}_6\\ \left[e\left(t-\tau \left(t\right)\right)+\frac{2}{{\tau }_2-\tau \left(t\right)}{\displaystyle {\int }_{t-{\tau }_2}^{t-\tau \left(t\right)}e\left(s\right)}\text{d}s-\frac{6}{{\left[{\tau }_2-\tau \left(t\right)\right]}^2}{\displaystyle {\int }_{t-{\tau }_2}^{t-\tau \left(t\right)}{\displaystyle {\int }_{\theta }^{t-\tau \left(t\right)}e\left(s\right)}}\text{d}s\text{d}\theta \right]\\ -\left({\tau }_2-\tau \left(t\right)\right){\displaystyle {\int }_{t-\tau \left(t\right)}^{t-{\tau }_1}{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)J_6\stackrel{\dot{}}{e}\left(s\right)\text{d}s}\end{array}$ (31)

根据引理3可得

$\begin{array}{l}-\left({\tau }_2-{\tau }_1\right){\displaystyle {\int }_{t-{\tau }_2}^{t-{\tau }_1}{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)}{J}_4\stackrel{\dot{}}{e}\left(s\right)\text{d}s-\left({\tau }_2-\tau \left(t\right)\right){\displaystyle {\int }_{t-\tau \left(t\right)}^{t-{\tau }_1}{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)J_6\stackrel{\dot{}}{e}\left(s\right)\text{d}s}\\ =-\left({\tau }_2-{\tau }_1\right)\left[{\displaystyle {\int }_{t-\tau \left(t\right)}^{t-{\tau }_1}+{\displaystyle {\int }_{t-{\tau }_2}^{t-\tau \left(t\right)}}}\right]{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)J_4\stackrel{\dot{}}{e}\left(s\right)\text{d}s-\left({\tau }_2-\tau \left(t\right)\right){\displaystyle {\int }_{t-\tau \left(t\right)}^{t-{\tau }_1}{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)J_6\stackrel{\dot{}}{e}\left(s\right)\text{d}s}\\ =-\frac{1}{{\rho }_1}\left(\tau \left(t\right)-{\tau }_1\right){\displaystyle {\int }_{t-\tau \left(t\right)}^{t-{\tau }_1}{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)J_4\stackrel{\dot{}}{e}\left(s\right)}\text{d}s-\frac{1}{{\rho }_2}\left({\tau }_2-\tau \left(t\right)\right){\displaystyle {\int }_{t-{\tau }_2}^{t-\tau \left(t\right)}{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)J_4\stackrel{\dot{}}{e}\left(s\right)\text{d}s}\\ -\frac{1-{\rho }_1}{{\rho }_1}\left(\tau \left(t\right)-{\tau }_1\right){\displaystyle {\int }_{t-\tau \left(t\right)}^{t-{\tau }_1}{\stackrel{\dot{}}{e}}^{\text{T}}\left(s\right)J_6\stackrel{\dot{}}{e}\left(s\right)}\text{d}s\end{array}$

$\begin{array}{l}\le -{\xi }^{\text{T}}\left(t\right)\left[E_1^{\text{T}}\left({\bar{J}}_4+{\bar{J}}_6\right)E_1+E_2^{\text{T}}{\bar{J}}_4{E}_2-E_1^{\text{T}}{\bar{J}}_6{E}_1\right]\xi \left(t\right)\\ -{\xi }^{\text{T}}\left(t\right)\left[{\rho }_2{\left(\begin{array}{c}{E}_1\\ E_2\end{array}\right)}^{\text{T}}\left(\begin{array}{cc}{\bar{J}}_4+{\bar{J}}_6-P_2{\bar{J}}_4^{-1}{P}_2{}^{\text{T}}& P_1\\ \ast & 0\end{array}\right)\left(\begin{array}{c}{E}_1\\ E_2\end{array}\right)\right]{\xi }^{\text{T}}\left(t\right)\\ -{\xi }^{\text{T}}\left(t\right)\left[{\rho }_1{\left(\begin{array}{c}{E}_1\\ E_2\end{array}\right)}^{\text{T}}\left(\begin{array}{cc}0& P_2\\ \ast & {\bar{J}}_4-P_1^T{\left({\bar{J}}_4+{\bar{J}}_6\right)}^{-1}{P}_1\end{array}\right)\left(\begin{array}{c}{E}_1\\ E_2\end{array}\right)\right]{\xi }^{\text{T}}\left(t\right)\end{array}$ (32)

$\begin{array}{l}0=2\left[e^{\text{T}}\left(t\right)+{\stackrel{\dot{}}{e}}^{\text{T}}\left(t\right)+e^{\text{T}}\left(t_s\right)\right]G\times [-\stackrel{\dot{}}{e}\left(t\right)+\left(A+\Delta A\left(t\right)\right)e\left(t\right)+\left(B+\Delta B\left(t\right)\right)e\left(t-\tau \left(t\right)\right)\\ +\left(E+\Delta E\left(t\right)\right)g\left(De\left(t\right)\right)-KC\left(e\left(t_s\right)-\epsilon \left(t_s\right)\right)]\end{array}$ (33)

$0\le -2{\left[g\left(De\left(t\right)\right)-K_{2}De\left(t\right)\right]}^{\text{T}}F\left[g\left(De\left(t\right)\right)-K_{1}De\left(t\right)\right].$ (34)

综上证明可得

$\stackrel{\dot{}}{V}\left(t\right)\le {\xi }^{\text{T}}\left(t\right)\left[{\Psi }_1+\frac{h-r\left(t\right)}{h}{\Psi }_2+\frac{r\left(t\right)}{h}{\Psi }_3+{\Psi }_4\left(\tau \left(t\right)\right)+LM\Delta \left(t\right)N+N^{\text{T}}{\Delta }^{\text{T}}\left(t\right)M^{\text{T}}{L}^{\text{T}}\right]\xi \left(t\right)$ (35)

根据引理4可得

$\stackrel{\dot{}}{V}\left(t\right)\le {\xi }^{\text{T}}\left(t\right)\left[{\Psi }_1+\frac{h-r\left(t\right)}{h}{\Psi }_2+\frac{r\left(t\right)}{h}{\Psi }_3+{\Psi }_4\left(\tau \left(t\right)\right)+{\epsilon }^{-1}LM{M}^{\text{T}}+\epsilon N^{\text{T}}N\right]\xi \left(t\right)$ (36)

基于引理5和6可知，若 ${\Psi }_1+\frac{h-r\left(t\right)}{h}{\Psi }_2+\frac{r\left(t\right)}{h}{\Psi }_3+{\Psi }_4\left(\tau \left(t\right)\right)+{\epsilon }^{-1}LM{M}^{\text{T}}{L}^{\text{T}}+\epsilon N^{\text{T}}N\le 0$ 成立，当且仅当下式成立：

${\Psi }_1+{\Psi }_i+{\Psi }_4\left(\tau \left(t\right)\right)+{\epsilon }^{-1}LM{M}^{\text{T}}{L}^{\text{T}}+\epsilon N^{\text{T}}N\le 0i=2,3;\tau \left(t\right)取值{\tau }_1,{\tau }_2$ (37)

4. 数值仿真

为了验证本文所提方法的有效性，做如下两个仿真：

例1. 时滞Chua’s电路形式如下：

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}_1\left(t\right)=a\left(x_2\left(t\right)-m_1{x}_1\left(t\right)+g\left(x_1\left(t\right)\right)\right)-c{x}_1\left(t-d\left(t\right)\right),\hfill \\ {\stackrel{\dot{}}{x}}_2\left(t\right)=x_1\left(t\right)-x_2\left(t\right)+x_3\left(t\right)-c{x}_1\left(t-d\left(t\right)\right),\hfill \\ {\stackrel{\dot{}}{x}}_3\left(t\right)=-b{x}_2\left(t\right)+c\left(2x_1\left(t-d\left(t\right)\right)-x_3\left(t-d\left(t\right)\right)\right),\hfill \end{array}$

其中，参数a = 9, b = 14.286, c = 0.1, m₀ = −1/7，m₁ = 2/7，时变时滞 $d\left(t\right)=\frac{e^t}{e^t+1}$，非线性函数 $g\left(x_1\left(t\right)\right)=\frac{1}{2}\left(m_1-m_0\right)\left(\left|x_1\left(t\right)+1\right|-\left|x_1\left(t\right)-1\right|\right)\in \left[0,1\right]$。

Chua’s电路可以表示成Lur’e系统的形式

$A=\left[\begin{array}{ccc}-a{m}_1& a& 0\\ 1& -1& 1\\ 0& -b& 0\end{array}\right],B=\left[\begin{array}{ccc}-c& 0& 0\\ -c& 0& 0\\ 2c& 0& -c\end{array}\right],E=\left[\begin{array}{c}-a\left(m_0-m_1\right)\\ 0\\ 0\end{array}\right],C=D={\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]}^T,$

主从系统的分别取初始值 $x\left(0\right)={[\begin{array}{ccc}0.2& 0.3& 0.2\end{array}]}^T,y\left(0\right)={\left[\begin{array}{ccc}-0.3& -0.1& 0.4\end{array}\right]}^T$，其他参数取值为 ${\kappa }_1=2,$ ${\kappa }_2=2,$ ${\mu }_1={\mu }_2=5,{\sigma }_1\left(0\right)=0.454,{\sigma }_2\left(0\right)=0.456$，根据理论1求解LMIs (15)~(17)，得到最大采样周期的值为h = 0.5248。本文与已有文献的最大采样周期数值的对比如表1所示。

Table 1. The maximum sampling period h

表1. 最大采样区间h

当h = 0.5248时，我们可以通过求解LMI，计算出事件触发阈值矩阵 ${\Theta }_i\left(i=1,2,3\right)$ 和控制增益矩阵K：

$\begin{array}{l}{\Theta }_1=\left(\begin{array}{ccc}0.9204& 0.2326& -0.3374\\ 0.2326& 0.7814& -0.2136\\ -0.3374& -0.2136& 0.9862\end{array}\right),{\Theta }_2=\left(\begin{array}{ccc}0.7108& -0.2953& 0.3854\\ -0.2953& 0.7476& 0.2204\\ 0.3854& 0.2204& 0.7832\end{array}\right),\\ {\Theta }_3=\left(\begin{array}{ccc}0.7028& -0.2934& 0.3694\\ -0.2934& 0.7347& 0.2145\\ 0.3694& 0.2145& 0.7782\end{array}\right),K=\left(\begin{array}{c}3.5306\\ 0.3244\\ -3.1814\end{array}\right)\end{array}$

与之前文献选取的传统事件触发不同，本文选择了自适应事件触发机制。由图1可以看出，非线性函数 ${\sigma }_1\left(t\right),{\sigma }_2\left(t\right)$ 可以根据触发机制自动调节大小，直至趋于常数。由图2可以看出，当最大采样周期h = 0.5248时，误差系统可以在有限时间内趋于零，即具有时变时滞的Lur’e系统实现了主从同步。由图3可以看出在最大采样区间h = 0.5248时，主从同步过程中加入事件触发机制能够减少信号的传输次数，从而提高通信利用率。

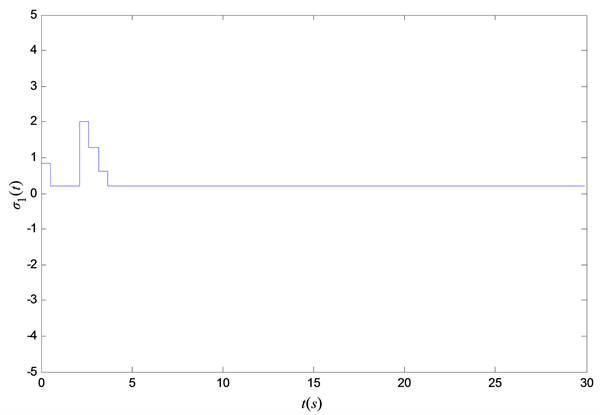
Figure 1. The trajectories of the nonlinear function ${\sigma }_1\left(t\right),{\sigma }_2(\; t\; )$

图1. 非线性函数 ${\sigma }_1\left(t\right),{\sigma }_2\left(t\right)$ 的变化轨迹

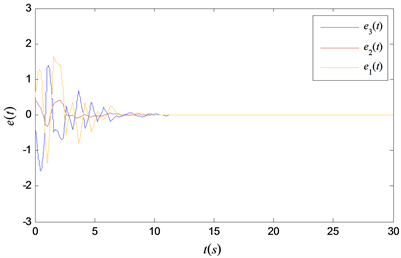
Figure 2. Response of e(t) with the sampling period of h = 0.5248

图2. 采样周期为0.5248时误差e(t)的响应曲线

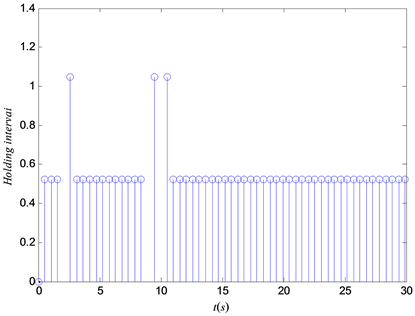
Figure 3. Transmission instants and releasing intervals of event-triggered

图3. 事件触发传输瞬间及其释放间隔

例2. 考虑如下不确定Lur’e系统，并给出参数矩阵：

$\stackrel{\dot{}}{e}\left(t\right)=\left(A+\Delta A\left(t\right)\right)e\left(t\right)+\left(B+\Delta B\left(t\right)\right)e\left(t-\tau \left(t\right)\right)+E\eta \left(De\left(t\right)\right)-KCe\left(t-h\left(t\right)\right),$

$A=\left[\begin{array}{ccc}-7.2& 1.6& 0.8\\ 1& -5.8& 0\\ 3& 11.25& -4\end{array}\right],B=0,E=\left[\begin{array}{c}3.7\\ 5.6\\ 4.1\end{array}\right],C=D={\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]}^T,$

$N_1=\left[\begin{array}{ccc}0.1& 0& 0\\ 0& 0.1& 0\\ 0& 0& 0.1\end{array}\right],N_2=0,N_3=\left[\begin{array}{c}0.1\\ 0\\ 0\end{array}\right],M=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right].$

主从系统的分别取初始值 $x\left(0\right)={\left[\begin{array}{ccc}-0.5& -0.8& 0.7\end{array}\right]}^T,y\left(0\right)={\left[\begin{array}{ccc}0.9& 0.2& -0.4\end{array}\right]}^T$。其他参数取值为 ${\kappa }_1={\kappa }_2=2,{\mu }_1={\mu }_2=5,{\sigma }_1\left(0\right)=0.454,{\sigma }_2\left(0\right)=0.456,\eta \left(\epsilon \right)=\left|\sin \left|\epsilon \right|\right|$。根据定理1，计算得最大采样区间h = 0.8131，求解LMI(15)~(17)所得控制器增益矩阵为 $K={\left[\begin{array}{ccc}\text{1}\text{.3905}& \text{1}\text{.5792}& \text{7}\text{.2932}\end{array}\right]}^T$。由表2可知本文所得最大采样区间h = 0.8131，优于已有文献 [21] [22] 的最大采样周期数值。

Table 2. The maximum sampling period h

表2. 最大采样周期h

当最大采样区间h = 0.3时，求得控制增益 $K={\left[\begin{array}{ccc}2.0970& 2.6300& 7.2642\end{array}\right]}^T$。图4是非线性函数 ${\sigma }_1\left(t\right)$, ${\sigma }_2\left(t\right)$ 的变化轨迹。图5是误差系统的轨迹变化。由图6可以看出，取最大采样区间h = 0.3时，主从同步过程中加入事件触发机制能够有效减少信号的传输次数，从而提高通信利用率。

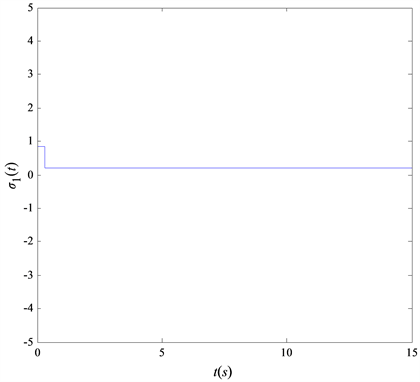
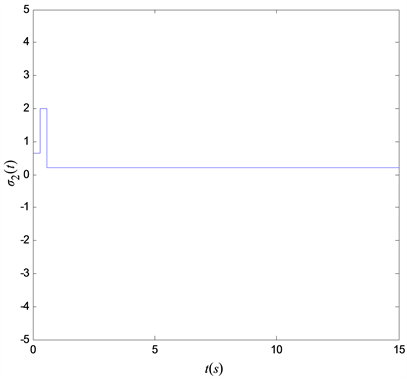
Figure 4. The trajectories of the nonlinear function ${\sigma }_1\left(t\right),{\sigma }_2(\; t\; )$

图4. 非线性函数 ${\sigma }_1\left(t\right),{\sigma }_2\left(t\right)$ 的变化轨迹

Figure 5. Response of e(t) with the sampling period of h = 0.3

图5. 采样周期为h = 0.3时误差e(t)的响应曲线

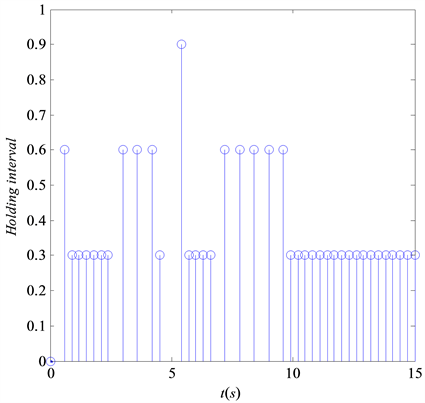
Figure 6. Transmission instants and releasing intervals of event-triggered

图6. 事件触发传输瞬间及其释放间隔

5. 结论

本文研究了基于事件触发机制的参数不确定Lur’e系统主从同步的问题。为了减少保守性，在构建Lyapunov-Krasovskii泛函时，考虑了非线性函数的约束条件。在Lyapunov-Krasovskii泛函求导过程中，应用基于辅助函数的积分不等式能够减少积分不等式的放缩，从而降低系统保守性。通过结合Lyapunov稳定性理论和线性矩阵不等式方法，给出了混沌Lur’e系统主从同步的充分条件。最后，通过数例仿真验证方法的有效性。从仿真结果中可以看出，本文引进事件触发机制，可以在通信网络中减少数据传输，从而实现缓解网络带宽的压力。

致谢

本文作者衷心感谢上海工程技术大学研究生科研创新项目(0232-E3-0903-19-01286)对本文的资助。

NOTES

^*通讯作者。