基于小波分析的信号去噪研究

Research on Signal Denoising Based on Wavelet Analysis

摘要: 本文主要通过小波分析理论对含噪声的非平稳信号进行去噪研究，分析了常见的信号滤波去噪方法的原理和特点，重点讨论了基于小波分析的去噪方法，并利用Matlab软件针对不同的去噪方法进行仿真实验，最后对以上几种方法进行评价总结。

Abstract: This paper, through the theory of wavelet analysis of non-stationary signal containing noise denoising research, analyzes the common principle and characteristics of signal filtering denoising method, discusses the denoising method based on wavelet analysis, uses MATLAB software for different denoising methods to carry out simulation experiments, and finally makes a conclusion of the several methods of the above.

1. 引言

信号在日常生活中无处不在，随着多媒体和信息技术的高速发展，如今的我们生活在一个数字化和信息化的时代。信号是运载信息的工具，同时也是信息的载体 [1] [2]。而在日常的实际应用中，许多信号都包含着各种尖峰、阶跃与突变，而且也不是均匀平衡的白噪声。所以为了克服传统傅里叶变换在局部处理上的局限性，我们有必要通过采取更好的方法来进行处理。本文主要通过小波分析来对非平稳信号进行降噪处理，并通过Matlab仿真实验对其他去噪方法进行对比，分析了在不同参数时小波方法对信号去噪效果的影响。

2. 非平稳信号

非平稳信号指的是分布参数或分布律随时间发生变化的信号 [3]。而非平稳信号的最主要特点是不满足线性，线性信号与非线性信号主要的区别在于是否满足叠加原理。即信号的输入输出是否具有可加性和齐次性的性质。我们可以简单地将其写成为：考虑一个系统 $S$，对应输入 $x\left(t\right)$ 和输出 $y\left(t\right)$ 应满足：

$m{x}_1\left(t\right)+n{x}_2\left(t\right)\to m{y}_1\left(t\right)+n{y}_2(\; t\; )$

其中m和n都是任意常数，t代表时间，事实上非平稳信号在本质上是时间的函数。

信号的所谓平稳与非平稳是根据其是否能满足平稳随机过程的条件而言的，主要的分析方法有时域分析、频域分析或者时频联合分析。

3. 一些常见的信号去噪方法及其特点

3.1. 均值滤波

一维均值滤波方法的原理是对信号的k-邻域的平均值来替代每个值来进行滤波处理，其中k为正整数，这是在局部邻域上进行处理的算法。我们不妨假设信号 $f\left(x\right)$ 是一族包含n个点的时间序列，在每个时间点 $x$ 上都对应着不同的信号值，相应地，通过均值滤波处理过后的信号为 $g\left(x\right)$。那么 $g\left(x\right)$ 的每个信号值是由包含 $\left(x,y\right)$ 邻域的信号值的平均值所决定的。以下给出具体的计算公式：

$g\left(x,y\right)=\frac{1}{S}{\displaystyle \underset{(x,y)\in U}{\sum }f\left(x,y\right)}$ (1)

式(1)中 $x,y=0,1,\cdots ,n-1$，U是以点 $\left(x,y\right)$ 为中心的邻域集合，S是U内时间点个数的总数。同时，在上式中也可以看出均值滤波是一种线性滤波。

虽然均值滤波具有算法简单且计算速度较快的优点，但这是以处理后结果会相对比较模糊为代价，尤其是在信号的细节和边缘处。

3.2. 中值滤波

中值滤波最早是由Turky在1971年提出的一种非线性滤波方法 [4]，其算法原理也与均值滤波相类似。两者的区别在于均值滤波利用的是邻域的信号值的平均值，而中值滤波则是利用其中位数。在实际运算中只需将式(1)中的求和算子改成求中位数算子，从而信号也不再满足叠加原理，这也是中值滤波是非线性的原因。同时，由于中值滤波不需要用到信号的统计特性等数据(如信号的熵值、期望、方差等等)，在实际应用是使用较为方便。

我们以具体的例子来说明这两种滤波方法的区别：现有一时间序列{2, 2, 3, 3, 4, 4}，分别以2-邻域的均值滤波和中值滤波进行处理，滤波后结果分别为：{7/3, 5/2, 14/5, 16/5, 7/2, 11/3}，{2, 5/2, 3, 3, 7/2, 4}。

3.3. 快速傅里叶变换

快速傅里叶变换FFT (Fast Fourier Transform)是基于计算机对离散傅里叶变换(DCT)的计算方法。考虑如下长度为N的有限长时间序列 $x={\left\{x_k\right\}}_{k=1}^N$，则其对应的DCT可以表示成 ${\hat{x}}_k={\displaystyle \underset{j=0}{\overset{N-1}{\sum }}x\left(j\right)\exp }\left(-\frac{2\pi ikj}{n}\right)$。其中i为虚数单位。而FFT则是利用计算机程序的计算特点对DCT的求解过程进行优化加速处理。

4. 小波分析

小波分析源自于Fourier分析，是传统Fourier分析思想方法的新发展和新延拓，能够有效地克服传统Fourier分析在时域和频域中不能同时进行局部化信号处理的劣势 [5]。小波变换具有时频联合分析的优点，有着良好的自适应性，即能够在不同频段使用不同尺度的函数对信号进行逼近处理达到最优化，非常适用于处理各种带有尖峰、突变等非平稳信号。

由于实际中信号的有用部分主要集中在低频范围，噪声和细节部分主要集中在高频范围的特点，为了去除噪声提高信号质量，我们在对信号进行去噪处理时的关键步骤 [6] [7] [8] 有以下几步：

1) 先要对含噪信号进行小波分解，我们先选择一个合适的小波基函数和要对它进行分解的层次k，这里k是一个正整数，然后计算出含噪信号到第k层的分解。

2) 然后是对信号的高频系数进行阈值量化处理，在每一层中选择一个合适阈值对该层的高频系数进行量化。

3) 最后是对含噪信号的小波重构，我们根据小波分解过后的第k层的低频系数和经过处理后的从第1层到第k层的高频系数来计算它的小波重构。

其算法流程图如图1所示：

Figure 1. Flow chart of wavelet denoising

图1. 小波去噪流程图

5. 仿真实验与结果对比

5.1. 信号去噪方法的对比

基于以上算法流程，我们应用Matlab软件来对实际信号进行去噪处理。考虑以下实际原始含有突变的矩形波信号，并对其添加高斯噪声，原始信号和含噪信号如下图2所示，并经计算知原始信号和含噪信号的SNR (信噪比)和MSE (均方误差)值分别为13.2342和0.6318。

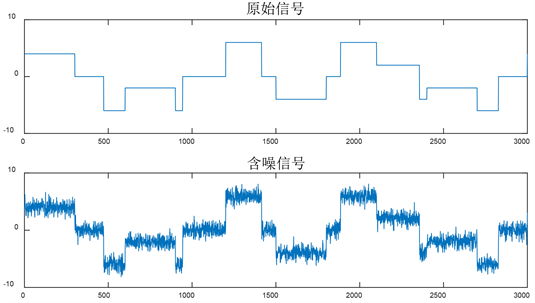
Figure 2. Original signal and noisy signal

图2. 原始信号和含噪信号

我们分别利用均值滤波、中值滤波、快速FFT和小波分析进行去噪，并调整不同去噪方法的参数进行对比分析，综合结果如下图3所示：

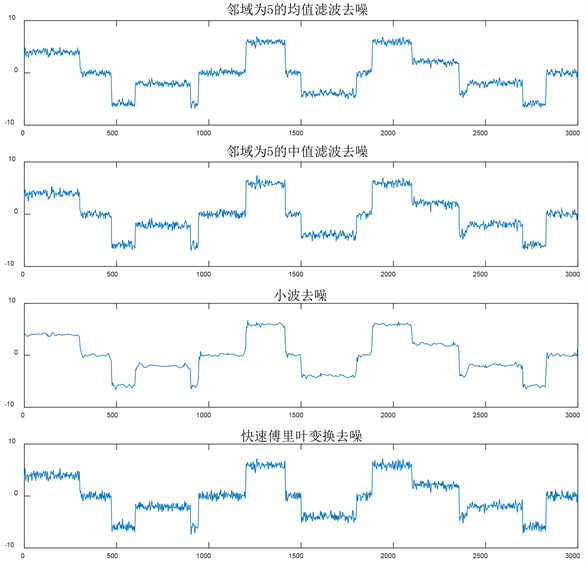
Figure 3. Comparison of various denoising methods

图3. 各种去噪方法的对比

上述去噪后信号与原始信号的SNR和MSE值如下表1所示：

Table 1. Signal quality evaluation index of different denoising methods

表1. 不同去噪方法的信号质量评价指标

其中，SNR值代表的是信号里的有效信号的能量与噪音的能量之比值，其值越高说明混在信号里的噪声值最小。MSE值反映着去噪后信号与原始信号的差异程度，其值越低说明去噪后信号与原始信号的接近程度越高 [9]。

从上述实验结果和信号质量评价指标中可以看到，对于非平稳信号，尤其是对于含有突变、尖峰、方波的信号，小波去噪方法对比其他方法可以取得更好的信号去噪效果。而且从视觉上看，小波去噪方法处理后相比其他几种更加平滑，更接近于原始信号。

不难看出，快速FFT对于非平稳信号的去噪效果不大，其SNR和MSE值指标也和其他方法对比性能较差，不能较好地还原真实的原始信号。这是因为快速FFT的处理是在频率域上对信号分析，但不能分辨出含有突变、尖峰的信号，这是快速FFT在时域上的弊端。而小波能联合时间和频率域进行分析，故能取得较好的去噪效果。

5.2. 不同参数对小波方法去噪的影响

简单来说利用小波方法去噪主要是三个步骤：分解、阈值量化和重构，其中选择合适的阈值函数和对阈值进行估计是关键。

在经过分解后得到信号与噪声对应的小波系数，由于信号系数要比噪声的大，所以我们可以选取一个合适的 $\lambda$ 作为阈值，若分解系数小于 $\lambda$ 则舍弃。当大于 $\lambda$ 时，硬阈值方法是直接保留，而软阈值则是按某一固定量收敛于零 [10]。通常来说，软阈值具有良好的数学特性，连续性好且较为平滑，但也正因如此，使用软阈值会丢失掉一些信号的细节部分；硬阈值一般对应着简单的处理方法。

不仅如此，选择合适的小波分解层数也是影响去噪的重要因素。

以下通过仿真实验例子予以说明，如图4所示。

我们同时给出上述参数的信号评价指标，如表2所示。

Table 2. Signal evaluation index of different parameters in wavelet method

表2. 小波方法中不同参数的信号评价指标

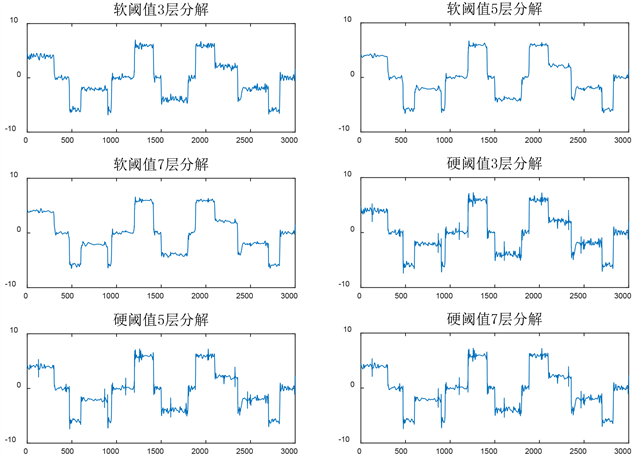
Figure 4. Influence of various parameters on wavelet denoising

图4. 各种参数对小波去噪的影响

从表2中可以看出，并不是分解层数越高越好，也会出现SNR值有所降低，同时MSE值也随之增加的情况，这说明和原始信号的差别也在增大，而且去噪效果从直观视觉和数值指标上看效果都不太好，反而影响了其去噪效果。所以选择合理的分解层数也是影响去噪效果的重要因素。其次，软阈值方法的SNR和MSE值性能均由于硬阈值，这样正好反映了软阈值方法较为平滑、具有良好数学特性的特点。

6. 结束语

本文分析了两种常见的信号滤波方法和快速FFT对信号去噪的算法原理和特点，重点讨论了基于小波方法对含有突变的非平稳信号进行处理，并比较了几种方法的去噪效果。结合主观的视觉感受和客观评价指标，通过仿真实验例子说明小波方法处理非平稳信号的优越性，同时在实际问题的处理中需要注意选择合适的分解层数和阈值函数。

本文仍有许多的不足之处，例如缺少对阈值估计方法和选取小波基函数的讨论、缺少对小波方法的具体算法的展开等等。以上这些都是需要不断改进的方面，希望在接下来的学习和研究中能够有所突破。

基金项目

省级大学生创新创业训练计划项目(S201910576059)；广东省自然科学基金项目(2019A1515011320, 2021A1515010292)；广东省普通高校特色创新项目(2020KTSCX134)；广东省本科高校教学质量与教学改革工程建设项目(2018179-17)。