1. 引言
近几年,间断有限元方法(DG方法)在诸多领域获得广泛应用。DG方法最早是由Reed和Hill在求解中子输运方程时提出 [1],之后其他学者进行了DG方法的误差分析并获得了最优收敛阶。经过数十年的发展,目前已出现了多种DG方法。这些DG方法大致可以分为两大类:基于数值通量形式的DG方法和基于内部罚函数的DG方法。第一类基于数值通量形式的DG方法主要用于求解双曲方程,以Cockburn和Shu提出的求解双曲守恒律方程的Runge-Kutta DG (RK-DG)有限元方法具有代表性 [2] [3]。Cockburn和Shu提出了几种常用的数值通量,适用于各种不同情况。在实际应用中,学者可以针对不同的方程构造独特的数值通量以满足实际情况 [4] [5],和其他差分格式相比可以达到更高收敛阶 [6],所以应用的更为广泛。
2. 波动方程及其间断有限元方法
2.1. 波动方程
以带有初值条件的一维无源声波方程为例,其方程形式如下:
首先对方程进行降阶处理,使其化为满足守恒律的形式。引入位移变量
,满足如下的关系:
将其带入原声波方程中,并进行积分得到满足双曲守恒律的方程组:
为简化方程,引入以下记号:则方程可以写成
至此,通过引入新的变量将二阶声波方程转化为一阶方程组,并满足守恒律的要求 [7]。
2.2. 空间域间断有限元方法
对一阶方程组
进行空间离散。首先将求解区域
划分为K个不重叠的单元
去逼近计算区域
,在单元上选取
个节点。区域划分如图1所示:

Figure 1. Element division of calculation area
图1. 计算区域单元剖分
引进线性映射如下:将每个计算单元变换到区间[−1, 1]上。
在求解区域上构建试验函数空间:
,在单元上把局部解用
阶多项式表示:
。
构造残量
,现要求残量正交于
中所有的试验函数 [8],即
经过一次分部积分得到DG方法弱形式如下,其中
表示局部外法向量,在一维问题中是一个标量。
在图1中,如果对试验函数和局部解没有约束条件,在单元界面上就可能会出现多个值
,必须选择一个合适的解来进行接下来的计算。这就是数值通量的选择,目前先将其记为
[6]。
通过再一次分部积分,可以得到DG方法的强形式如下,这是计算常用的形式。
将残量
带入上式积分得到:
其中:
.
接下来将局部解的表达式带入,即可得到一阶方程组的DG方法的强形式,如下:
其中:
为线性映射的Jacobi,
。
和
之间存在如下的计算关系:
至此即完成了DG方法的空间离散。
2.3. 时间离散
完成空间域离散后,可以得到半离散问题如下,其中
为未知量。此时问题的求解为常微分方程 [9]。
经典的基于数值通量的RK-DG方法采用Runge-Kutta进行时间离散,这是一种经典的单步法 [7]。一般的高阶Runge-Kutta时间离散格式表达式如下 [10]:
其中当
时,上述时间离散格式的精度是
阶。在这里选取变形的四阶显式RK方法(ERK):其基本形式如下,相关系数可查阅文献 [5] 得到。
3. 计算方法的实现
在本节将介绍计算过程中选取的基函数、数值积分计算以及数值通量选择选择等。
3.1. 基函数
如果考虑基函数
,在计算过程中需要计算单元质量矩阵
,随着多项式次数的增加,得到的质量矩阵条件数很差,因为
一个稳妥的办法是选择一组规范正交基来计算,可以通过对基函数进行Gram-Schmidt直交化来实现。其计算形式如下:
为传统的n阶Lengendre多项式。由此基函数得到的质量矩阵要优于简单基函数。
3.2. 数值积分
从DG方法的强形式可以看出,计算中需要大量的积分运算。如果使用精确积分,会导致巨大的计算量,因此可以考虑使用数值积分进行计算,同时计算格式要满足精度要求。根据已有经验来看,对于K次多项式积分运算,单元内部的积分应该使用精度至少为2K次的数值积分格式,对于单元边界上的积分,应使用精度至少为2K + 1次的格式。
目前使用较为广泛的是采用Legendre-Gauss-Lobatto (LGL)积分点进行积分 [11]。该积分点与等距节点积分和Gauss积分不同,等距积分形成的矩阵随着多项式次数的增加会出现列几乎线性相关的情况,不利于计算。Gauss积分通过张量积形式形成高维情形时,节点会集中在积分区域内部。而LGL积分点可以通过其他方法避免这些情况。查阅相关文献可以得到LGL积分点的计算方法,得到积分点与积分权重。
3.3. 数值通量
关于数值通量的选择,首选具有相容性、守恒性、单调性的数值通量。此种类型的数值通量最初来自于求解双曲守恒律方程的高分辨率格式的构造上,它不仅具有高精度,而且还能保持数值格式的稳定性和收敛性,具有很好的数学性质 [4] [5]。
首先定义单元边界处的平均值
以及沿法向的跳跃
如下,其中
表示单元内部极限值,
表示单元外部极限值。
目前常用的满足如上性质的数值通量函数有:
,
代表中心通量,
代表迎风通量。
Lax-Friedrichs通量:
,其中C与计算区域的情况有关。
目前,在声波方程的计算中比较常用的是Lax-Friedrichs通量,其计算公式相对简单,但不会影响计算的精度。
3.4. 时间步长
为了保持数值算法的稳定性,空间、时间步长需要满足一定的关系式,对该方法进行冯·诺伊曼稳定性分析,以便知道数值
的值是什么。
由条件
确保其
稳定性,因为只有在这种条件下,舍入误差才不会被放大 [5]。
例如,对于使用k次多项式和k + 1阶达到k + 1次的RK方法(k + 1阶精度)的DG离散,实际中可以采取
。此外,对于
,数值
比
数值估算值小5% [5]。故在本文中时间步长满足
,其中空间步长为
,C为传播中最大速度。
4. 数值实验
本节将通过两个例子来验证DG方法的计算效果。
4.1. 一阶单波方程
先来看一个一阶简单线性波动方程,该方程具有初值,形式如下:
.
该问题的精确解为
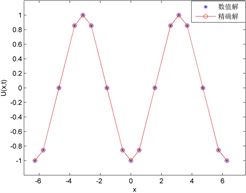
。对于单个方程,其DG方法要比方程组更简单,这里便不再重复。图2为一阶波方程DG方法数值解与精确解的比较,其中单元基函数选取为4阶,区域剖分为4段(a)、8段(b)和16段(c),数值通量选为中心通量,最终时间为
,可以看出计算结果误差较小。
 (a)
(a) 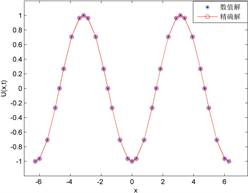 (b)
(b) 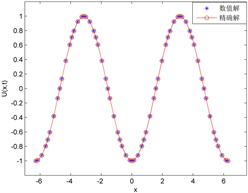 (c)
(c)
Figure 2. Comparison between numerical solution and exact solution of first-order wave equation
图2. 一阶波动方程数值解与精确解的比较
同时我们还计算了在不同单元个数K和多项式阶数N情况下的
误差以及收敛阶,从表1中可以看出:随着单元剖分个数的增加和多项式阶数的提高,收敛阶始终趋于
阶 [12]。

Table 1. Error and convergence order of numerical solution
表1. 数值解的误差与收敛阶
4.2. 二阶波动方程
对于二阶波动方程,带有初值条件如下:其中选取波速
,计算区间为
。
.
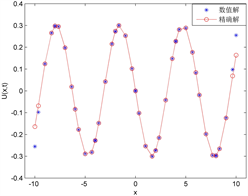
在实际计算中,选取3阶基函数进行插值,数值通量选为Lax-Friedrichs通量,最终计算时间为
。结果如图3:其中a为计算空间10等分,b为计算空间20等分,c为计算空间30等分。
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 3. Comparison between numerical solution and exact solution of second-order wave equation
图3. 二阶波动方程数值解与精确解的比较
对其进行误差分析和收敛阶计算,即使用N阶多项式模拟时,随着剖分单元数的增加,收敛阶逐渐趋向于
阶。
5. 结论
在本文中,通过对二阶无源波动方程空间域进行间断有限元离散,在时间上采用经典的Rutta-Kutta方法进行离散,得到了较高的收敛阶,这和DG方法的理论分析是一致的。在计算过程中,选取经Gram-Schmidt直交化的Lengendre多项式作为基函数,避免了随着多项式阶数的提高质量矩阵条件数变坏的情况。数值积分选取LGL积分点和权重,避免了等距积分形成行列式线性相关的情况,时间离散上采用采用经典的Rutta-Kutta单步法四阶变形形式,减少了计算中的存储用量。最后通过两个实例分析验证了间断有限元方法可以获得更高的收敛阶,并且提高多项式的阶数要比传统有限元更方便,在未来会获得更广泛的应用。
基金项目
中国石油大学(北京)科研基金项目资助(编号:2462020XKJS02)。