Burgers方程的时空Legendre谱配置方法

Space-Time Legendre Spectral Collocation Methods for Burgers Equation

摘要: 利用Legendre-Gauss-Lobatto节点为配置点，构造Burgers方程初边值问题的时空Legendre谱配置格式。即在时间和空间方向都用Lagrange插值多项式将其化为非线性方程组，数值实验证明了所提算法格式的有效性和高精度。

Abstract: A Legendre spectral collocation scheme is constructed for Burgers equation by using the Legendre collocation method in time and space, which is a nonlinear system using Lagrange interpolation polynomials. Numerical results demonstrate the efficiency and high accuracy of the proposed algorithm.

1. 引言

Burgers方程由Bateman 1915年在研究流体运动时提出 [1]。浅水波以及一些物理系统中的波动过程可以归结为Burgers方程。一维Burgers方程精确解首先由Benton和Platzman得到 [2]，因此，求解Burgers方程是科学或工程领域中的重要课题。一些作者用Chebyshev谱–Euler混合方法、高阶紧致有限体积、时空耦合谱元方法和迎风LDQ方法求解Burgers方程初边值问题 [3] [4] [5] [6]。由于时间和空间方向的误差阶不同，导致时间和空间方向的模数不平衡，这就会增加计算工作量，为克服这个局限性，有作者对发展型方程构造了时空谱方法 [7] [8]。最近，一些作者研究了以Legendre-Gauss-Lobatto节点为配置点的微分矩阵的一些性质 [9] [10]，并用于求解常微分方程定解问题的数值解 [11] [12]，特别有作者构造了KdV方程Cauchy问题的时空谱配置方法 [13] [14]，基于这些工作，本文构造Burgers方程初边值问题的时空Legendre谱配置方法，具体地就是考虑如下Burgers方程初边值问题：

$\{\begin{array}{ll}{\partial }_{s}u+u{\partial }_{x}u-{\partial }_x^{2}u=0,\hfill & x\in \left(-1,1\right),s\in \left(0,T\right],\hfill \\ u\left(-1,s\right)=g_1\left(s\right),u\left(1,s\right)=g_2\left(s\right),\hfill & s\in \left[0,T\right],\hfill \\ u\left(x,0\right)=\phi \left(x\right),\hfill & x\in \left[-1,1\right].\hfill \end{array}$ (1)

用Lagrange二元插值多项式逼近(1)的精确解，在时间和空间方向用Legendre谱配置方法，将(1)式化为非线性矩阵方程，然后转化为非线性代数方程组，利用通常的不动点迭代方法求得数值解，显然在函数关于时间和空间两个变量充分光滑时，两个方向的数值误差阶是相同的，都具有谱精度，并且大大地减少了计算工作量。

2. 基于Gauss节点的插值多项式及其微分矩阵

记 $L_N\left(x\right)\left(x\in I=\left(-1,1\right)\right)$ 为N次Legendre多项式。 $x_0=-1;x_N=1;x_k\left(1\le k\le N-1\right)$ 是 ${\partial }_x{L}_N\left(x\right)=0$ 的根 [11]。以 $x_k$ 为节点的Lagrange插值基函数为：

${\psi }_k\left(x\right)=\frac{\left(1-x^2\right){\partial }_x{L}_N\left(x\right)}{N\left(N+1\right)\left(x_k-x\right)L_N\left(x_k\right)}.$ (2)

记 $P_N\left(I\right)$ 为次数不超过 $N$ 的多项式集合，对 $u\left(x\right)\in C\left(\bar{I}\right)$，其Lagrange插值多项式

$p_N\left(x\right)={\displaystyle \underset{j=0}{\overset{N}{\sum }}{u}_j}{\psi }_j\left(x\right),u_j=u\left(x_j\right),x\in I.$

对 $p_N\left(x\right)$ 关于 $x$ 求 $m$ 阶导数，并令 $x=x_k,k=0,1,\cdots ,N$，得

${\partial }_x^m{p}_N\left(x\right)={\displaystyle \underset{j=0}{\overset{N}{\sum }}{u}_j}{\partial }_x^m{\psi }_j\left(x\right).$

相应于 ${\psi }_j\left(x\right)$ 的 $m$ 阶微分矩阵和一阶微分矩阵分别记为：

$D^{(m)}={\left({\partial }_x^m{\psi }_j\left(x_k\right)\right)}_{0\le k,j\le N},{\begin{array}{cc}& D=D^{(1)}=\left(d_{kj}={\partial }_x{\psi }_j\left(x_k\right)\right)\end{array}}_{0\le k,j\le N}.$

引理 根据文献 [9] 中的(3.68)和(3.203)式，则有 [9] [10] [11]：

$d_{kj}=\{\begin{array}{ll}-\frac{N\left(N+1\right)}{4},\hfill & k=j=0;\hfill \\ \frac{L_N\left(x_k\right)}{\left(x_k-x_j\right)L_N\left(x_j\right)},\hfill & k\ne j;\hfill \\ \frac{N\left(N+1\right)}{4},\hfill & k=j=N;\hfill \\ 0,\hfill & k=j,\left(k,j=1,2,\cdots ,N-1\right).\hfill \end{array}$ (3)

而且m阶微分矩阵是一阶微分矩阵的m次幂。

3. Burgers方程初边值问题的谱配置格式

对(1)式作变换 $t=\frac{2s}{T}-1$，问题转化为：

$\{\begin{array}{ll}\frac{2}{T}{\partial }_{t}u+u{\partial }_{x}u-{\partial }_x^{2}u=0,\hfill & x\in \left(-1,1\right),t\in \left(-1,1\right],\hfill \\ u\left(-1,t\right)=g_1\left(s\left(t\right)\right),u\left(1,t\right)=g_2\left(s\left(t\right)\right),\hfill & t\in \left[-1,1\right],\hfill \\ u\left(x,-1\right)=\phi \left(x\right)\hfill & x\in \left[-1,1\right].\hfill \end{array}$ (4)

记 $\Omega =I\otimes I,$ 及 $Q_{M,N}\left(\Omega \right)=P_M\left(I\right)\otimes P_N\left(I\right)$。式(4)的Legendre时空谱配置方法就是求 $u_{M,N}\left(x,t\right)\in Q_{M,N}\left(\Omega \right)$ 满足：

$\{\begin{array}{ll}\frac{2}{T}{\partial }_t{u}_{M,N}+u_{M,N}{\partial }_x{u}_{M,N}-{\partial }_x^2{u}_{M,N}=0,\hfill & x\in \left(-1,1\right),t\in \left(-1,1\right],\hfill \\ u_{M,N}\left(-1,t\right)=g_1\left(s\left(t\right)\right),u_{M,N}\left(1,t\right)=g_2\left(s\left(t\right)\right),\hfill & t\in \left[-1,1\right],\hfill \\ u_{M,N}\left(x,-1\right)=\phi \left(x\right),\hfill & x\in \left[-1,1\right].\hfill \end{array}$ (5)

用 $u_{M,N}\left(x,t\right)={\displaystyle \underset{n=0}{\overset{N}{\sum }}{\displaystyle \underset{m=0}{\overset{M}{\sum }}{\hat{u}}_{m,n}}}{\psi }_n^{}\left(x\right){\psi }_m\left(t\right)$ 逼近(4)式的解，并将其带入到(5)式中，得：

$\{\begin{array}{l}\frac{\text{2}}{T}{\displaystyle \underset{n=0}{\overset{N}{\sum }}{\displaystyle \underset{m=0}{\overset{M}{\sum }}{\hat{u}}_{m,n}}}{\psi }_n^{}\left(x_k\right){\partial }_t{\psi }_m\left(t_l\right)+{\displaystyle \underset{n=0}{\overset{N}{\sum }}{\displaystyle \underset{m=0}{\overset{M}{\sum }}{\hat{u}}_{m,n}}}{\psi }_n^{}\left(x_k\right){\psi }_m\left(t_l\right){\displaystyle \underset{n=0}{\overset{N}{\sum }}{\displaystyle \underset{m=0}{\overset{M}{\sum }}{\hat{u}}_{m,n}}}{\partial }_x{\psi }_n^{}\left(x_k\right){\psi }_m\left(t_l\right)\\ -{\displaystyle \underset{n=0}{\overset{N}{\sum }}{\displaystyle \underset{m=0}{\overset{M}{\sum }}{\hat{u}}_{m,n}}}{\partial }_x^2{\psi }_n^{}\left(x_k\right){\psi }_m\left(t_l\right)=0,k=1,2,\cdots ,N-1;l=1,2,\cdots ,M,\\ {\displaystyle \underset{n=0}{\overset{N}{\sum }}{\displaystyle \underset{m=0}{\overset{M}{\sum }}{\hat{u}}_{m,n}}}{\psi }_n^{}\left(x_0\right){\psi }_m\left(t_l\right)=g_1\left(\frac{t_l+1}{2}T\right),{\displaystyle \underset{n=0}{\overset{N}{\sum }}{\displaystyle \underset{m=0}{\overset{M}{\sum }}{\hat{u}}_{m,n}}}{\psi }_n^{}\left(x_N\right){\psi }_m\left(t_l\right)=g_2\left(\frac{t_l+1}{2}T\right),\\ l=0,1,\cdots M,{\displaystyle \underset{n=0}{\overset{N}{\sum }}{\displaystyle \underset{m=0}{\overset{M}{\sum }}{\hat{u}}_{m,n}}}{\psi }_n^{}\left(x_k\right){\psi }_m\left(t_0\right)=\phi \left(x_k\right),k=0,1,2,\cdots ,N.\end{array}$ (6)

记 ${\hat{d}}_{l,m}^{}={\partial }_t^{}{\psi }_m\left(t_l\right),$ ${\tilde{d}}_{k,n}={\partial }_x^{}{\psi }_n\left(x_k\right),{\tilde{d}}_{k,n}^{(\text{2})}={\partial }_x^{\text{2}}{\psi }_j\left(x_k\right)$，利用Lagrange插值多项式的性质，式(6)关于 $l$ 、 $k$ 展开，则(6)式可转化成矩阵形式为：

$AX-X{B}^{\text{T}}+X.*D=-X.*\left(X{C}^{\text{T}}\right)-F.$ (7)

用 $E_n$ 表示 $n$ 阶单位矩阵，“ $\otimes$ ”表示Kronecker积， $G$ 是矩阵 $D$ 按行向量拉长后的转置向量， $R$ 是矩阵 $F$ 按行向量拉长后的转置向量，“ $.*$ ”表示对应元素相乘，则(7)式可化为如下的非线性方程组：

$\left(A\otimes E_{N-1}-E_M\otimes B\right)Y+Y.*G=-Y\text{.*}\left(\left(E_M\otimes C\right)Y\right)-R.$ (8)

$\begin{array}{l}Y={\left({\hat{u}}_{1,1},{\hat{u}}_{1,2},\cdots ,{\hat{u}}_{1,N-1},{\hat{u}}_{2,1},{\hat{u}}_{2,2},\cdots ,{\hat{u}}_{2,N-1},\cdots ,{\hat{u}}_{M,1},{\hat{u}}_{M,2},\cdots ,{\hat{u}}_{M,N-1}\right)}^{\text{T}},\\ Y_0={\left({\hat{u}}_{0,1},{\hat{u}}_{0,2},\cdots ,{\hat{u}}_{0,N-1},0,0,\cdots ,0,\cdots ,0,0,\cdots ,0\right)}^{\text{T}},\\ R={\left(f_{1,1},f_{1,2},\cdots ,f_{1,N-1},f_{2,1},f_{2,2},\cdots ,f_{2,N-1},\cdots ,f_{M,1},f_{M,2},\cdots ,f_{M,N-1}\right)}^{\text{T}},\\ G={\left(d_{1,1},d_{1,2},\cdots ,d_{1,N-1},d_{2,1},d_{2,2},\cdots ,d_{2,N-1},\cdots ,d_{M,1},d_{M,2},\cdots ,d_{M,N-1}\right)}^{\text{T}}.\end{array}$

4. 数值结果

Burgers方程有精确孤波解及初边值 [15]：

$\begin{array}{l}u\left(x,s\right)=\frac{2\frac{\omega }{k}{\text{e}}^{\frac{-\omega }{\alpha k^2}(kx-\omega s)}}{C_1+{\text{e}}^{\frac{-\omega }{\alpha k^2}(kx-\omega s)}},\phi \left(x\right)=\frac{2\frac{\omega }{k}{\text{e}}^{\frac{-\omega }{\alpha k^2}kx}}{C_1+{\text{e}}^{\frac{-\omega }{\alpha k^2}kx}},\\ g_1\left(s\right)=\frac{2\frac{\omega }{k}{\text{e}}^{\frac{-\omega }{\alpha k^2}(-k-\omega s)}}{C_1+{\text{e}}^{\frac{-\omega }{\alpha k^2}(-k-\omega s)}},g_2\left(s\right)=\frac{2\frac{\omega }{k}{\text{e}}^{\frac{-\omega }{\alpha k^2}(k-\omega s)}}{C_1+{\text{e}}^{\frac{-\omega }{\alpha k^2}(k-\omega s)}}.\end{array}$ (9)

这里 $k,\omega ,\alpha$ 和 $C_1$ 都是常数。

在(1)式中时间方向令 $T=1$。用下面的 $L^{\infty }-$ 范数度量数值误差

$E_{M,N}=\underset{1\le l\le M,1\le k\le N-1}{\max }\left|u_{M,N}\left(x_k,t_l\right)-u\left(x_k,t_l\right)\right|.$

图1是(1)式中时间方向 $T=1$，(9)式中的参数 $k=\text{0}\text{.5},\omega =\text{0}\text{.3},C_1=2\omega /k,\alpha =1$，时间方向插值多项式次数 $M=\text{7}$ 时最大值误差 $E_{M,N}$ 随空间插值多项式次数 $N$ 的变化情况，可以看出误差随 $N$ 的增大而快速减小，算法格式在空间方向有谱精度，而且空间方向和时间方向所用的模数相差不大，算法格式平衡了两个方向的代价，这是所提算法的一个优点。

图2的参数和图1相同，空间方向插值多项式次数 $N=1\text{5}$ 时最大值误差 $E_{M,N}$ 随时间插值多项式次数 $M$ 的变化情况，表明算法格式在时间方向有谱精度。

图3的参数和图1的参数相同，表明在迭代30次时CPU所耗费的时间秒数，表明算法格式的高效性。

图4是(1)式中时间方向 $T=10$，(9)式中的参数 $k=\text{0}\text{.5},\omega =\text{0}\text{.3},C_1=2\omega /k,\alpha =1$，时间方向插值多项式次数 $M=20$ 时最大值误差 $E_{M,N}$ 随空间插值多项式次数 $N$ 的变化情况，可以看出算法格式对(1)式中时间方向 $T$ 取较大值仍然得到很好的结果。

Figure 1. $L^{\infty }-$ error with $M=\text{7},k=\text{0}\text{.5},\omega =0.3,C_1=2\omega /k,\alpha =1$

图1. $M=\text{7},k=\text{0}\text{.5},\omega =0.3,C_1=2\omega /k,\alpha =1$ 时的 $L^{\infty }-$ 误差

Figure 2. $L^{\infty }-$ error with $N=15,k=\text{0}\text{.5},\omega =\text{0}\text{.3},C_1=2\omega /k,\alpha =1$

图2. $N=15,k=\text{0}\text{.5},\omega =\text{0}\text{.3},C_1=2\omega /k,\alpha =1$ 时的 $L^{\infty }-$ 误差

Figure 3. Costing seconds of CPU with $M=\text{7},k=\text{0}\text{.5},\omega =\text{0}\text{.3},C_1=2\omega /k,\alpha =1$

图3. $M=\text{7},k=\text{0}\text{.5},\omega =\text{0}\text{.3},C_1=2\omega /k,\alpha =1$ 时CPU耗费时间秒数

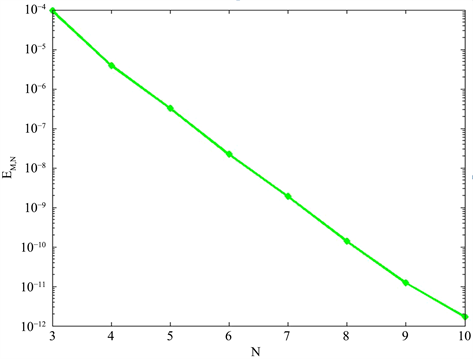
Figure 4. $L^{\infty }-$ error with $M=\text{20},k=\text{0}\text{.5},\omega =\text{0}\text{.3},C_1=2\omega /k,\alpha =1$

图4. $M=\text{20},k=\text{0}\text{.5},\omega =\text{0}\text{.3},C_1=2\omega /k,\alpha =1$ 时的 $L^{\infty }-$ 误差

5. 结论

本文针对Burgers方程初边值问题用时空Legendre-谱配置方法构造了问题的二元Lagrange插值逼近格式，利用已有的微分矩阵将Burgers方程转化为非线性矩阵方程，再转化为等价形式的非线性方程组，利用通常的不动点迭代求解。算法格式简单有效，数值实验表明在时间和空间方向所用节点数相差很小，总节点个数 $21\le MN\le 200$，大大地减少了工作量，这是所提算法的主要优点。另外，本文所提算法格式也可以用来求解其他经典的数学物理问题。

基金项目

国家自然科学基金(批准号：11371123)；河南科技大学srtp基金(批准号：202010464053)；河南自然科学基金(批准号：202300410156)。