1. 引言
电气设备由导电、绝缘和导磁材料等组成,运行过程中会受到电力、热力、机械力和环境等诸多因素的影响,很容易发生劣化,使其出现设备故障。不仅带来巨大的经济损失,而且还要承担生命健康的风险 [1]。因此需要保障设备的安全,定期对设备进行必要的检测和维修。通过研究电力设备的检测新方法,对于保障设备安全、提高运行效率和减小事故发生等方面都具有重要意义 [2]。数字图像处理作为电力行业中设备检测的重要手段,更是决定了检测效果的优劣。图像的边缘信息是图像分割、识别和压缩等高层次图像处理问题的基石,因此边缘检测效果的好坏非常关键 [3]。
传统的图像边缘检测算法优点为形式简单,计算量小,但均有不同方面的缺点。例如像Robert、Prewitt算子等一阶微分算子和Canny、Laplacian、Log算子这样的二阶微分算子,边缘检测效果比较差,对图像噪声非常敏感,所以在实际应用中受到非常多的限制 [4]。另外还有不少工作者从不同角度对边缘检测进行了探讨,这里只提几个研究成果:Caselles (1994)等人提出了测地线活动轮廓模型 [5];Chan (2006)将水平集方法应用到图像分割 [6];Shi等人(2020)在边缘检测中加入了先验信息 [7]。
近年来,数学形态学因其简单性和高效性受到了大家的极大关注,进而涌现出了各式各样的改进方案,但是依旧存在不同程度的缺陷。例如Peter (2016)结合模糊变换及图像的数学结构,通过形态学方法填补图像,可以准确定位图像区域,取得了比较好的效果,但是降噪能力低,计算过程复杂 [8];徐剑锋等人(2017)运用单一尺度的菱形结构元素,虽然算法实现容易,但提取的边缘会出现中断现象 [9];闫俊红等人(2018)采用两种尺度不同的结构元素来对图像进行交替滤波运算,虽然提高了边缘检测的准确性,但是此算法只对部分噪声类型有效 [10]。
因此,如何精准地检测到边缘细节和消除不同噪声带来的干扰是边缘检测的重要课题。本文首先简单介绍数学形态学方法中涉及的基本理论概念。其次,综合考虑图像边缘的多尺度和多方向特性,基于数学形态学方法提出一种合理高效的边缘检测算法。最后,数值试验考虑了变压器、电力塔和绝缘子三类不同的电力设备图像,三种不同噪音,并将本文算法和三种传统边缘检测算法进行了比较。边缘检测结果图明显可以看出本文所提算法得到的边缘完整且精确,并且噪音的去除效果最好。同时通过品质因数和信噪比两个定量指标比较了不同算法的优劣。
2. 数学形态学理论
结构元素(也称模板)是数学形态学的基本算子,主要作用为与特定的图像区域进行逻辑运算后可以输出期望结果。常见结构元素有方形、线形、扁平形、圆形等形状,结合不同的图像,选取合适的结构元素是提高边缘检测性能的重要方法。一般情况下,结构元素的选择应遵循以下两个原则:1) 确保结构元素的简洁性和有界性;2) 结构元素尽量选择几何上具有凸性的子集。如果选择非凸子集,不仅不能提取有效信息,而且会增加大量无用信息 [11]。
当结构元素选取之后,就是如何与图像进行数学形态学运算。最基本运算包括膨胀和腐蚀。腐蚀可以去除一些毛刺和小的凸起,消除物体边缘点,用
表示。膨胀与腐蚀互为对偶运算,但并不互为逆运算。膨胀可以填充图像中的孔洞和狭窄缝隙,用
表示。另外,开运算
是对图像先腐蚀再膨胀,可以平滑图像边缘,去掉长的突起、边缘、毛刺和孤点。闭运算•是对图像先膨胀再腐蚀,可以消除细长的鸿沟和狭窄的间断,并能填补边缘轮廓线中的裂痕,从而使图像边缘更加光滑。
3. 改进算法
传统数学形态学方法用于图像边缘检测是对一幅图像利用单一结构元素,这样得到的边缘通常色调暗、有断带,还会造成部分边缘信息的损失、遗漏,而且不能用于复杂形状的图像 [12]。这里将融合方形结构与线性结构元素各自的优势,一方面是实现全方位、高精准地检测图像边缘,另一方面可以更好地抑制噪声的影响。
3.1. 多方向
线性结构元素是有多个方向的,图1表示0˚、45˚、90˚和135˚四个方向的3 × 3线性结构元素。

Figure 1. Three by three structural elements in four directions
图1. 4个方向的3 × 3结构元素
当使用0˚方向结构元素进行边缘检测时,能够提取出垂直方向上的边缘信息,而接近水平方向的边缘细节会被遗漏;同样,当利用90˚方向结构元素时,水平方向上的边缘可以检测出来,但是垂直方向上的边缘细节同样丢失;这样,采用45˚和135˚方向结构元素检测也有类似情况。如果线性结构元素的方向与待检测边缘为垂直状态时,可以达到最佳匹配 [13]。所以进行边缘检测时,使用线性结构元素必须考虑多个方向,避免丢失一些边缘信息。而图像的边缘实质上是图像中像素值发生突变的像素点的集合,也就是说位于图像边缘上的像素点的像素值会发生突变,某个方向上的梯度值会明显大于其它三个方向的梯度值 [14]。综合利用以上四个方向的边缘信息,可以提取出全方位多角度的边缘细节。具体过程中需要求以下几个关键量:
1) 灰度距离
图2中的
为3 × 3的图像子块的像素值,灰度距离
。灰度距离反映了子块中心像素点与其邻域像素点之间的差异,差异越大表示像素点之间变化程度越剧烈,该像素点作为边缘点的概率越大。
2) 边缘马氏灰度距离
设中心点p1处的坐标为
,根据上面的灰度距离,可以计算中心点
处的边缘马氏灰度距离:
(1)
其中,D1、D2、D3、D4分别对应0˚、45˚、90˚、135˚四个方向上的边缘情况。
那么,对于一幅大小为M × N的图像来说,可以通过下式来计算图像在4个不同方向上的边缘马氏灰度距离:
(2)
同理,ED1、ED2、ED3、ED4分别代表为0˚、45˚、90˚、135˚方向上的边缘马氏灰度距离。
3) 各方向结构元素权值的计算
令
,可以计算出在0˚、45˚、90˚、135˚四个方向上的结构元权值
,
,
,
:
(3)
通过上式计算出最佳结构元素,可以减少大量不必要的计算,加快了检测速度,提高了算法的效率,检测出的边缘图像效果更好 [15]。
3.2. 多尺度
同时,注意到大尺寸结构元素的抗噪特性好,可以用来抑制噪声;小尺度结构元素的边缘定位特性好,可以获得准确的边缘位置。多种尺度的结构元素结合起来,一起作用于图像,抑制噪声的同时可以获得非常好的边缘信息 [16]。
方形结构元素(元素全为1)对边缘细节的提取要优于线性,尤其当方形结构元素尺寸为3 × 3时,对边缘的检测最准确精细。因为标准差反映的是像素值与均值的离散程度,可以说标准差越大,图像的质量就越好 [17]。其中标准差的计算公式如下:
(4)
(5)
其中,M × N表示图像的大小,
表示第x行、第y列的像素值,
表示均值。
因此尺度权重就可以围绕标准差来计算,利用不同尺度下边缘图像的标准差来计算不同尺度的权重,最后加权平均求得最终的边缘图像,效果不错。具体步骤如下:
1) 依次求出各尺度下的图像边缘Ei;
2) 然后计算各边缘图像的标准差
;
3) 则不同尺度结构元素的权重为:
(6)
4) 最终取得的边缘图像为:
(7)
3.3. 多尺度与多方向融合
线性结构元素在抑制噪声方面要强于方形结构元素,方形结构元素的尺度和形状都会影响图像边缘检测的效果。这里将运用多尺度与多方向融合的思想,来进一步改进边缘检测的效果。
对于线性结构元素,设i (i = 1, 2, 3, 4)代表尺度的大小,当i=1时,表示结构元素的尺度大小为3 × 3;当i = 2时,表示结构元素的尺度大小为5 × 5;当i = 3时,表示结构元素的尺度大小为7 × 7;当i = 4时,表示结构元素的尺度大小为9 × 9。同样用j (j = 1, 2, 3, 4)表示结构元素的方向,当j = 1时,表示结构元素的方向是0˚;当j = 2时,表示结构元素的方向是45˚;当j = 3时,表示结构元素的方向是90˚;当j = 4时,表示结构元素的方向是135˚。那么bi,j就可以用来代表不同尺度不同方向的结构元素。例如,b1,1表示方向为0˚的尺度为3 × 3线性结构元素。
其中,MATLAB中创建结构元素的方式可以用strel命令,具体函数为:strel (‘shape’, parameters),其中shape为形状参数;parameters为与结构元素相关的大小或方向的参数。例如建立一个45˚,尺寸为5 × 5的线性结构元素b2,2:b2,2 = strel (‘line’, 5, 45)。
通过上面分别对多尺度和多方向结构元素的选择以及权重确定的探讨,提出一种基于数学形态学方法的多尺度多方向图像边缘检测算法,具体步骤如下:
(I) 对于噪声图像,可通过中值滤波与高斯滤波结合的方法进行去噪预处理。然而对于无噪声图像,则无需执行此步骤;
(II) 综合考虑除噪和边缘提取的效果,选用相对来说最有优势的抗噪腐蚀型算子:
(f为待检测图像;b为线性结构元素)。即对于i尺度,j方向的线性结构元素,提取到的图像边缘为
;
(III) 分别计算在0˚、45˚、90˚、135˚四个方向上的权值
,
,
,
;
(IV) 分别对每一尺度的线性结构元素在不同方向进行加权求和:
,得到线性结构元素在4个不同尺度的边缘图像。
而对于3 × 3的方形结构元素,通过多种算子对边缘提取的效果进行对比,发现腐蚀型算子对边缘的提取最为全面,因此方形结构元素提取的边缘图像为:
(此式中I = 5,b5为3 × 3的方形结构元素)。
(V) 根据
来计算标准差
;
(VI) 计算结构元素各个尺度的权值
,得到最终的边缘图像
。
4. 实验结果及分析
数值仿真实验选取电力设备图像三大类别中的典型代表:变压器、电力塔和绝缘子,并与常用的Robert、Log及Canny方法进行对比,来验证本文所提算法的可行性和有效性。数值模拟仿真环境为Matlab7.0。数值试验考虑了图像无噪声(图3~6)和有噪声(图7~10)两种情况。从电力设备原图中可以看出,电网图像中有很多电线或者电力塔类似的线型边缘,精确定位难度大,其中变压器还有阴影的干扰。
4.1. 视觉直观分析
对比不同算法的检测效果,可以通过直接的视觉观察去判别。不仅仅是检测原图像的边缘,还给不同图像加不同噪声,以便达到横向与纵向双重对比,使实验更加有说服力。
1) 首先是对原图像进行数值实验,各个不同类型的边缘对比情况如下(图3~6):


 变压器 电力塔 绝缘子
变压器 电力塔 绝缘子
Figure 3. Original images of transformers, power towers and insulators
图3. 变压器、电力塔和绝缘子的原图像



 Robert Log Canny (阈值:0.05) 本文算法
Robert Log Canny (阈值:0.05) 本文算法
Figure 4. Comparison diagram of transformer edge detection effect
图4. 变压器边缘检测效果对比图


 Robert Log Canny (阈值:0.05) 本文算法
Robert Log Canny (阈值:0.05) 本文算法
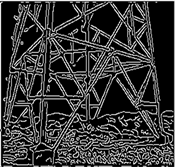
Figure 5. Comparison diagram of edge detection effect of power tower
图5. 电力塔边缘检测效果对比图


 Robert Log Canny (阈值:0.02) 本文算法
Robert Log Canny (阈值:0.02) 本文算法
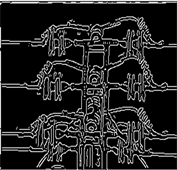
Figure 6. Comparison diagram of insulator edge detection effect
图6. 绝缘子边缘检测效果对比图
2) 对变压器、电力塔和绝缘子分别加入泊松、高斯和椒盐噪声的边缘检测效果(图7~10):


 变压器(泊松噪声) 电力塔(高斯噪声)绝缘子(椒盐噪声)
变压器(泊松噪声) 电力塔(高斯噪声)绝缘子(椒盐噪声)
Figure 7. Noise images of transformers, power towers and insulators
图7. 变压器、电力塔和绝缘子的噪声图像



 Robert Log Canny (阈值:0.15) 本文算法
Robert Log Canny (阈值:0.15) 本文算法
Figure 8. Comparison of transformer (Poisson noise) edge detection effect
图8. 变压器(泊松噪声)边缘检测效果对比



 Robert Log Canny (阈值:0.15) 本文算法
Robert Log Canny (阈值:0.15) 本文算法
Figure 9. Comparison of edge detection effect of power tower (Gaussian noise)
图9. 电力塔(高斯噪声)边缘检测效果对比



 Robert Log Canny (阈值:0.2) 本文算法
Robert Log Canny (阈值:0.2) 本文算法
Figure 10. Comparison of insulator (salt and pepper noise) edge detection effect
图10. 绝缘子(椒盐噪声)边缘检测效果对比
从实验结果能够看出,不论是无噪声图像还是带噪声图像,当目标图像稍加复杂时,通过Robert算子检测的结果都会遗漏大量的边缘信息,边缘检测效果最差。虽然Log算子的检测结果相对来说要比Robert算子好一点,但是检测出来的边缘连续性不好,也会出现边缘遗漏的现象,而且难以分辨出来真正的边缘细节,且受噪声的影响较大。Canny算子对于边缘信息的提取以及抗噪性能虽优于前两种,但是因为实际的电网图像蕴含的细节繁多复杂,所以检测结果依旧会出现断裂和漏检的情况,并且会存在伪边缘,去噪效果也不是很好 [18]。除此之外,对不同的图像和不同噪音进行边缘检测时,容易得到边缘过多或丢失的情况,还需对canny算法中调用的函数edge (图像,“Canny”,阈值)不断调整阈值参数(图7~10选取了视觉效果最好的阈值),缺乏灵活性和准确性。
对于本文提出的多尺度多方向数学形态学算法来说,优势比较明显:1) 抑制噪音能力强,能够检测出更多的边缘细节;2) 检测出的边缘非常清晰完整,连续性好;3) 边缘定位更准确;4) 普适性强,对不同图像和不同噪音无需设置参数;5) 算法简单,易实现。
4.2. 客观数据分析
除了直接人眼观察评判不同方法的效果优劣,还可以通过边缘检测评价指标来进行定量分析。本文采用的是品质因数(F)和信噪比(SNR)。
1) 品质因数
评价边缘检测性能品质因数(F)的测度公式是由Abdou和Patt等人给出的,其表达式为:
(8)
式中EA是指理想状态下的图像边缘像素的总数,ER表示实际检测出的图像边缘像素的总数,
是对于惩罚错位边缘的设计常数(一般取为1/9) [19],l表示实际边缘与理想边缘间的距离。F的值在0到1之间,F值越接近1,表明最后得到的结果与理想边缘越贴近 [20]。表1和表2表示应用不同算法和不同图像计算出的品质因数F的值。

Table 1. The value of F for clean images
表1. 无噪声图像F的数值

Table 2. The value of F for noisy images
表2. 噪声图像F的数值
通过表1和表2的数据可以看出本文算法的品质因数F明显接近于1,且远远超过其它几种算法。说明边缘提取非常全面精确,进一步表明了本文算法在边缘检测方面强大的优势性。
2) 信噪比
为了更好地评判本文算法的去噪效果,引入信噪比(SNR)作为客观数据,下式为SNR的计算公式:
(9)
其中M和N分别对应图像的行数和列数,
是在无噪声情况下的边缘图像,
为有噪声情况下的边缘图像。从计算公式中可以看出,SNR值越大,表明除噪效率越高 [21]。通过上述公式,分别计算出不同算法的SNR值,如下表3所示:

Table 3. SNR of edge detection effect
表3. 边缘检测效果的SNR
通过几种算法的对比可以看出,本文提出的多尺度多方向数学形态学边缘检测算法,信噪比SNR的数值要明显高于其它三种算法,验证了本文算法具有高效的除噪性能,也与视觉观察所得出的结论相符。
不论从直观的视觉角度去观察图像的边缘检测结果,还是客观地运用评判指标去分析,本文的数学形态学算法效果都要显而易见。提取到的图像边缘不仅完整,而且去噪性能也有很好的提升,对于电力图像的实用性更强。
4.3. 边缘检测在电力行业的应用
如何能实现直观、实时的监测电力设备运行状况一直是研究的热点,同时对电网运行具有重要意义。其中,运用图像边缘检测法监测电力设备正是其种要的应用领域之一。
目前主要是利用安装在监测终端的摄像机采集数字图像,通过网络传输到监控主机,然后对采集图像进行灰度变换、滤波处理、阈值变换、边缘检测等过程,以获得电力设备的边缘轮廓,由此判断电力设备的运行状况。
例如1) 通过与标定的设备边缘图像比较计算,即可识别出电力设备在运行过程中的变化情况,目前该方法多运用在分割绝缘子红外图像和计算输电线路覆冰厚度等方面;也可识别出导线断股、绝缘子片破损和杆塔塔材损坏变形等故障,可及时促使电力工作人员及时排除故障隐患,保证电力系统安全运行;2) 通过边缘检测方法对其提取出设备的边缘图像,实现设备红外图像的倾斜校正;3) 将火焰的边缘检测出来,而且直观反映出火焰的锋面位置以及温度场的分布情况;4) 图像边缘检测是输变电设备故障检测或获取关键信息的重要方法;5) 在故障条件下,采用复合成像技术对电力设备进行图像采集,对采集的电力设备复合成像进行角点匹配和边缘轮廓特征提取,采用三维区域轮廓扫描方法进行电力设备故障部位的信息增强和分段融合检测处理,实现电力设备故障复合成像检测。
5. 结束语
本文充分考虑了电力图像的特点,提出了基于自适应权值的多尺度多方向数学形态学边缘检测算法。此算法结合了不同结构元素的尺度大小和方向,不仅在理论分析上证明了算法的有效性和准确性,也通过具体的数值实验,验证了本文算法在图像边缘的检测方面具有以下优势:完整性高、定位准确、普适性强、连续性好、同时也具有完备的抗噪性能。本文所提供的边缘检测算法为电力行业的图像边缘检测提供了良好的借鉴意义。
基金项目
北京市自然科学基金(No. Z200001)。
NOTES
*第一作者。
#通讯作者。