一维反应扩散问题的时空谱元方法

A Space-Time Spectral Method for One-Dimensional Reaction-Diffusion Equation

摘要: 以一维反应扩散方程为模型，提出了一种时空谱元方法。在空间方向上应用局部间断Galerkin谱元法。在每个空间子区域上按Legendre-Galerkin方法生成格式，并且在边界处使用交替形式的数值流通量处理跳跃项。在时间方向上采用Legendre Dual-Petrov-Galerkin谱元法进行离散。给出了全离散格式的收敛性分析。线性及非线性问题的数值结果验证了该方法的有效性。

Abstract: Taking the one-dimensional reaction-diffusion equation as a model，a space-time spectral element method is proposed. We apply the local discontinuous Galerkin spectral element method in space direction. The scheme is formulated in the Legendre-Galerkin spectral form on each space subin-terval, while the inner boundary is dealt with alternating fluxes. The Legendre Dual-Petrov-Galerkin spectral element method is used to discretize the equation in time direction. The convergence analysis of the fully discrete scheme is given. The numerical results of some linear and nonlinear equations show the effectiveness of our method.

1. 引言

谱方法是一种以其高精度为主要优势的数值方法 [1] [2] [3]，被广泛地应用于求解偏微分方程。在对不可压缩的Navier-Stokes方程的研究中，Patera [4] 首次提出了将有限元的通用性和谱方法的准确性优势相结合的谱元法。通常，当空间方向上应用谱方法时，在时间方向上采用差分方法进行离散。差分方法的收敛阶是固定的。由此，当精确解在空间和时间两个方向上都足够光滑时，有必要考虑在空间和时间上同时采用谱方法进行求解。时空谱方法因此被提出 [5] [6]。

在1973年，Reed和Hill首次提出了间断Galerkin (DG)法。该方法其后由Johnson等推广应用 [7]。DG方法的主要特点在于，组成数值解空间和检验函数空间的分段多项式在子区域的边界处可以完全不连续。这也导致在子区域边界处存在歧义，因此将有限体积法中数值流通量的选取引入DG方法中。Cockburn和Shu [8] 首次提出了局部间断Galerkin (LDG)法，用于求解对流扩散方程。LDG方法的基本思想是通过引入辅助变量，将具有高阶导数的方程重写为一阶系统，然后将DG方法应用于重写后的系统。

反应扩散方程具有广泛的应用范围，在化学、物理、生物学等各个领域形成了大量的相关模型。在化学中的应用包括有Schnakenberg模型 [9]，Carburizing模型 [10] 等。在 [11] [12] 中给出了多种应用于物理和动力学中的反应扩散模型。在生物学各个方面也具有广泛的应用，如胚胎学 [13]，种群 [14] [15]，骨骼结构 [16] [17] 等。

对于在空间方向上应用DG方法或者谱方法，同时在时间方向上采用差分方法，进行离散求解反应扩散问题已存在大量研究。Zhang和Shu通过分析一维扩散方程DG方法的三种不同形式，得到了LDG方法和Baumann-Oden方法稳定且收敛的结论 [18]。Cao和Yang证明了Radau点上一维二维双曲问题及一维线性抛物问题的超收敛性 [19]。Yang和Shu在文献 [20] 中选取交替形式的数值流通量，应用LDG有限元方法求解一维线性抛物方程并分析其收敛性。在 [21] 中，作者在空间方向上使用Chebyshev拟谱法，结合时间方向上的Runge-Kutta法给出了稳定性结论。当问题的精确解在空间和时间方向上同时具有良好的光滑性时，部分研究者也采用时空谱方法进行求解。Tang和Ma采用空间傅里叶逼近时间Legendre Petrov-Galerkin法求解抛物方程 [22]。并且他们以一阶双曲方程为模型，在 [23] 中提出了一种时空谱方法，给出了该方法的收敛性分析。Shen和Wang提出了一种基于Legendre-Galerkin方法的时空谱方法求解一维抛物方程，并给出单区域的收敛性分析和数值结果 [24]。在 [25] 中，Guo和Wang针对广义非线性Klein-Gordon方程，提出了时间和空间方向上同时具有谱精度的配置方法。

本文考虑的一维线性反应扩散方程如下

${\partial }_{t}U-D{\partial }_x^{2}U=f\left(x,t\right),\left(x,t\right)\in \Omega =I_x\times J_t,$ (1)

其初始条件为

$U\left(x,-1\right)=U_0\left(x\right),x\in I_x,$

其中 $D>0$ 为常数， $I_x=\left(-1,1\right),J_t=\left(-1,1\right]$。为更简明地分析全离散格式的收敛性，考虑周期边界条件。对于非周期边界条件问题的处理可以参考 [26]。

在本文中，提出了一种时空谱元方法，并将其应用于一维反应扩散问题。在空间方向上采用LDG谱元法进行离散，有利于处理间断问题。谱元法可以减小问题的规模，允许在各子区域上选择不同次数的多项式，具有稳定性好、精度阶高和求解区域较灵活等优势。在时间方向上，应用Legendre dual-Petrov-Galerkin谱元法，该方法能很好地适用于奇数阶问题 [27]。这种方法的主要思想是应用一组满足问题边界条件的试探函数，同时采用一组满足“对偶”边界条件的检验函数。本文给出了全离散格式下的收敛性分析结果，并通过线性及非线性问题的多区域数值结果验证了方法的有效性和高精度特性。

本文的内容安排如下：第2节中给出了收敛性分析所需的有关定理、投影算子及其逼近结果；在第3节中给出了一维反应扩散方程的全离散格式，并简要阐述了线性及非线性问题的多区域数值算法；第4节中给出本文方法所得全离散格式的收敛性分析；第5节中给出了线性和非线性反应扩散方程的数值算例，并与其他研究方法所得结果进行对比；最后，在第6节中给出了对本文的总结。

2. 基本概念和引理

引入记号，记 ${\left(\cdot ,\cdot \right)}_{\Omega }$ 和 $\left|\right|\cdot |{|}_{\Omega }$ 分别为 $L^2\left(\Omega \right)$ 的内积和范数。设 $\sigma$ 为非负整数，并记 $H^{\sigma }\left(\Omega \right)$ 为通常的Sobolev空间，范数与半范数分别记为 $\left|\right|\cdot |{|}_{\Omega ,\sigma }$ 和 $|\cdot {|}_{\Omega ,\sigma }$ (当 $\Omega =I_x\times J_t$ 时，省去下标 $\Omega$ )。

令 $K_1,K_2$ 为正整数，将区间 $I_x=\left(-1,1\right)$ 分解成 $K_1$ 个子区域，其中 $I_i=\left(a_{i-1},a_i\right)$， $i=1,2,\cdots ,K_1$。记 $h_i^x=a_i-a_{i-1}$，有 $-1=a_0<a_1<\cdots <a_{K_1}=1$。将区间 $J_t=\left(-1,1\right]$ 分解为 $K_2$ 个子区域，其中 $J_j=\left(b_{j-1},b_j\right]，$ $j=1,2,\cdots ,K_2$。记 $h_j^t=b_j-b_{j-1}$，有 $-1=b_0<b_1<\cdots <b_{K_2}=1$。

引入仿射映射

$\begin{array}{l}v\left(x\right)=\bar{v}\left(\bar{x}\right),\hfill \end{array}x=\frac{1}{2}\left(h_i^x\bar{x}+a_{i-1}+a_i\right),\bar{x}\in I,x\in I_i,$

$v\left(t\right)=\bar{v}\left(\bar{t}\right),t=\frac{1}{2}\left(h_j^t\bar{t}+b_{j-1}+b_j\right),\bar{t}\in J,t\in J_j,$

其中 $\left(\bar{x},\bar{t}\right)\in \Omega ,\left(x,t\right)\in I_i\times J_j$。

令 $N=\left(N_1,N_2,\cdots ,N_{K_1}\right)$， $M=\left(M_1,M_2,\cdots ,M_{K_2}\right)$，其中 $N_i\left(1\le i\le K_1\right)$， $M_j\left(1\le j\le K_2\right)$ 为正整数。 ${\mathbb{P}}_{N_i}\left(I_i\right)$ 表示区间 $I_i$ 上次数不超过 $N_i$ 次多项式构成的空间， ${\mathbb{P}}_{M_j}\left(J_j\right)$ 表示区间 $J_j$ 上次数不超过 $M_j$ 次多项式构成的空间。不失一般性地，考虑 $U_0\left(x\right)\equiv 0$。初始值不为零的情况下考虑 $V=U-U_0$。

记

${\hslash }_i^x=\frac{h_i^x}{N_i},{\hslash }_j^t=\frac{h_j^t}{M_j},$

${\hslash }^x={\max }_{1\le i\le K_1}{\hslash }_i^x,{\hslash }^t={\max }_{1\le j\le K_2}{\hslash }_j^t.$

定义多项式空间

$V_N\left(I_x\right)=\left\{v:{v|}_{I_i}\in {\mathbb{P}}_{N_i}\left(I_i\right),1\le i\le K_1\right\},$

$Y_j^M\left(J_t\right)=\left\{v:{v|}_{J_j}\in {\mathbb{P}}_{M_j}\left(J_j\right),1\le j\le K_2\right\},$

$S_M\left(J\right)=\left\{v:v=\left(1+t\right)p\left(t\right),p\left(t\right)\in Y_j^{M-1}\right\},$

$S_M^{*}\left(J\right)=\left\{v:v=\left(1-t\right)p\left(t\right),p\left(t\right)\in Y_j^{M-1}\right\}.$

定义 ${\displaystyle {\prod }_{N,M}^C:}C\left(\bar{I}\times \bar{J}\right)\to V_N\times V_M$ 是由 ${\displaystyle {\prod }_{N_i,M_j}^C:}C\left(\bar{I}\times \bar{J}\right)\to {\mathbb{P}}_{N_i}\left(I_i\right)\times {\mathbb{P}}_{M_j}\left(J_j\right)$ 生成的二维Chebyshev-Gauss-Lobatto (CGL)插值算子

${\overline{\left({\displaystyle {\prod }_{N,M}^{C}u}\right)}}^{i,j}={\displaystyle {\prod }_{N_i,M_j}^C{\bar{u}}^{i,j}},1\le i\le K_1,1\le j\le K_2,$

其中

$\left({\displaystyle {\prod }_{N_i,M_j}^{C}u\left(x_k^i,t_l^j\right)}\right)=u\left(x_k^i,t_l^j\right),1\le k\le N,1\le l\le M,1\le i\le K_1,1\le j\le K_2,$

以上 $x_k^i,t_l^j$ 是 $I_i$ 和 $J_j$ 上的CGL点。

对于空间方向的投影算子，令 ${\mathcal{P}}_N^x$ 为 $L^2\left(I_x\right)$ 投影算子，即对 $i=1,2,\cdots ,K_1$，满足

${\displaystyle {\int }_{I_i}\left({\mathcal{P}}_N^{x}w\left(x\right)-w\left(x\right)\right)}v\left(x\right)\text{d}x=0,\forall v\in {\mathbb{P}}_{N_i}\left(I_i\right).$

定义特殊投影算子 ${\mathcal{P}}_N^{\pm }$ [28] $:H^1\left(I\right)\to V_N\left(I_x\right)$ 满足

${\displaystyle {\int }_{I_i}\left({\mathcal{P}}_N^{+}w\left(x\right)-w\left(x\right)\right)}v\left(x\right)\text{d}x=0,\forall v\in {\mathbb{P}}_{N_i-1}\left(I_i\right),{\mathcal{P}}_N^{+}w\left(x_{i-1}^{+}\right)=w\left(x_{i-1}\right),$

${\displaystyle {\int }_{I_i}\left({\mathcal{P}}_N^{-}w\left(x\right)-w\left(x\right)\right)}v\left(x\right)\text{d}x=0,\forall v\in {\mathbb{P}}_{N_i-1}\left(I_i\right),{\mathcal{P}}_N^{-}w\left(x_{i+1}^{-}\right)=w\left(x_{i+1}\right),$

其中 $x_i^{\pm }$ 是 $x$ 在 $i$ 点处得左右极限值。

引理2.1 [29] 若 $u\in H^{\sigma }\left({\Omega }_k\right)\left(\sigma \ge 1\right)$，对 $0\le s\le \min \left(N_k+1,\sigma \right)$，则有

${\Vert {\omega }^e\Vert }_{{\Omega }_k}\le C{h}^s{\left(\frac{\Gamma \left(N_k+2-s\right)}{\Gamma \left(N_k+2+s\right)}\right)}^{\frac{1}{2}}{\left|u\right|}_{s,{\Omega }_k},$ (2)

其中 ${\omega }^e=U-\mathcal{P}U$ 或 ${\omega }^e=U-{\mathcal{P}}^{\pm }U$。

设 $P_M^{\alpha ,\beta }:L_{\alpha ,\beta }^2\left(J_t\right)\to {\mathbb{P}}_M\left(J_t\right)$ 为带权 ${\omega }_{\alpha ,\beta }$ 的正交投影算子，满足

${\left(P_M^{\alpha ,\beta }u,v\right)}_{{\omega }_{\alpha ,\beta }}={\left(u,v\right)}_{{\omega }_{\alpha ,\beta }},\forall v\in {\mathbb{P}}_M\left(J_t\right),$

记 ${\omega }_{\alpha ,\beta }={\left(1-t\right)}^{\alpha }{\left(1+t\right)}^{\beta }$。

定义

${\tilde{H}}^1\left(J_t\right):=\left\{v:v\in H^1\left(J_t\right)\cap L_{{\omega }_{0,-1}}^2\left(J_t\right)\right\},{\hat{H}}^1\left(J_t\right):=\left\{v:v\in H^1\left(J_t\right)\cap L_{{\omega }_{0,-2}}^2\left(J_t\right)\right\}.$

类似 [24] 定义时间上的正交投影算子 $P_M^{0,-1}:{\tilde{H}}^1\left(J_t\right)\to S_M$，满足

${\left(P_M^{0,-1}v-v,\varphi \right)}_{J_t,{\omega }_{0,-1}}=0,\forall \varphi \in S_M.$

可知对任意 $v\in {\hat{H}}^1\left(J_t\right),\phi \in S_M^{*}$ 有

${\left({\partial }_t\left(P_M^{0,-1}v-v\right),\phi \right)}_{J_t}=-{\left(P_M^{0,-1}v-v,{\partial }_t\phi \right)}_{J_t}=-{\left(P_M^{0,-1}v-v,{\omega }_{0,1}{\partial }_t\phi \right)}_{J_t,{\omega }_{0,-1}}=0,$

实际上，因为 ${\omega }_{0,1}{\partial }_t\phi \in S_M$，由投影性质可得以上等式成立。

$H_{{\omega }_{0,-1}}^s\left(J_t\right)=\left\{u\in H^1\left(J_t\right)\cap L_{{\omega }_{0,-1}}^2\left(J_t\right):{\partial }_x^{l}u\in H^l\left(J_t\right)\cap L_{{\omega }_{l,l-1}}^2\left(J_t\right),1\le l\le s\right\}.$

由以上分析可得如下逼近结果。

引理2.2 [30] 若 $v\in H_{{\omega }_{0,-1}}^s\left(J_t\right)$ 且 $M={\min }_{1\le k\le K}{M}_k,h={\max }_{1\le k\le K}{h}_k$ 有

${\Vert {\partial }_t^l\left(P_M^{0,-1}v-v\right)\Vert }_{J_t,{\omega }_{l,l-1}}\le C{M}^{l-1}{\displaystyle \underset{k=1}{\overset{K}{\sum }}{\left(h_k^{-1}{M}_k\right)}^{1-s}}{\Vert {\partial }_t^{s}v\Vert }_{J_k},0\le l\le s,l=0,1．$ (3)

显然地，根据 $M$ 和 $h$ 的定义，可以得到以下估计

$\begin{array}{c}{\Vert {\partial }_t^l\left(P_M^{0,-1}v-v\right)\Vert }_{J_t,{\omega }_{l,l-1}}\le C{M}^{l-1}{\left(h^{-1}M\right)}^{1-s}{\Vert {\partial }_t^{s}v\Vert }_{J_t}\\ \le C{h}^{s-1}{M}^{l-s}{\Vert {\partial }_t^{s}v\Vert }_{J_t}\\ =C{h}^{l-1}{\hslash }_t{}^{s-l}{\Vert {\partial }_t^{s}v\Vert }_{J_t},\\ 0\le l\le s,l=0,1.\end{array}$

定义离散算子 $\mathcal{D}$，在每一个子区域 $K_j=\left(x_{j-1},x_j\right)$ 上

${\mathcal{D}}_{K_j}\left(\eta ,\varphi ;\hat{\eta }\right)=-{\left(\eta ,{\varphi }_x\right)}_{K_j}+{\left(\hat{\eta }{\varphi }^{-}\right)}_j-{\left(\hat{\eta },{\varphi }^{+}\right)}_{j-1},\mathcal{D}\left(\eta ,\varphi ;\hat{\eta }\right)={\displaystyle \underset{j}{\sum }{\mathcal{D}}_{K_j}}\left(\eta ,\varphi ;\hat{\eta }\right).$

引理2.3 [31] 对任意 $\varphi \in V_N$ 有

$\mathcal{D}\left(\eta -{\mathcal{P}}^{-}\eta ,\varphi ;{\left(\eta -{\mathcal{P}}^{-}\eta \right)}^{-}\right)=0,\mathcal{D}\left(\eta -{\mathcal{P}}^{+}\eta ,\varphi ;{\left(\eta -{\mathcal{P}}^{-}\eta \right)}^{+}\right)=0.$ (4)

引入分段的Sobolev空间

${\tilde{H}}^{\sigma }\left(\Omega \right)=\left\{v:v^{i,j}\equiv {v|}_{{\Omega }_{i,j}}\in H^{\sigma }\left({\Omega }_{i,j}\right),1\le i\le K_1,1\le j\le K_2\right\},$

其上的半模定义为

${\left|v\right|}_{{\tilde{H}}^{\sigma }(\Omega )}:={\left|v\right|}_{\sigma }={\left({\displaystyle \underset{i=1}{\overset{K_1}{\sum }}{\displaystyle \underset{j=1}{\overset{K_2}{\sum }}{\left|v^{i,j}\right|}_{\sigma ,{\Omega }_{i,j}}^2}}\right)}^{\frac{1}{2}}.$

3. 全离散格式及算法

首先引入中间变量 $P=\sqrt{D}{U}_x$，则(1)式可改写为以下形式

$\{\begin{array}{l}{\partial }_{t}U-\sqrt{D}\left(P_x\right)=f,\hfill \\ P=\sqrt{D}{U}_x.\hfill \end{array}$ (5)

其全离散格式为：寻找 $u,p\in V_N\otimes S_M$，使得对任意的 $v,z\in V_N\otimes S_M^{*}$ 有

$\{\begin{array}{l}{\left({\partial }_{t}u,v\right)}_{I_i\times J_j}+\sqrt{D}\left[-{\displaystyle {\int }_{J_j}{\left(\hat{p}\cdot v^{-}\right)}_{i,t}}\text{d}t+{\displaystyle {\int }_{J_j}{\left(\hat{p}\cdot v^{+}\right)}_{i-1,t}}\text{d}t+{\left(p,w_x\right)}_{I_i\times J_j}\right]={\left(f,v\right)}_{I_i\times J_j},\hfill \\ {\left(p,z\right)}_{I_i\times J_j}+\sqrt{D}\left[-{\displaystyle {\int }_{J_j}{\left(\hat{u}\cdot z^{-}\right)}_{i,t}}\text{d}t+{\displaystyle {\int }_{J_j}{\left(\hat{u}\cdot z^{+}\right)}_{i-1,t}}\text{d}t+{\left(u,z_x\right)}_{I_i\times J_j}\right]=0,\hfill \end{array}$ (6)

其中“ $\stackrel{^}{}$ ”表示数值流通量。在本文中，我们选取如下交替形式的数值流通量，这有助于其后对于时空局部间断谱元法全离散格式收敛性的证明。

$\hat{u}\left(x_i,t\right)=u\left(x_i{}^{-},t\right),\hat{p}\left(x_i,t\right)=p\left(x_i{}^{+},t\right),$

且

$v_{i,t}^{-}=v\left(x_i{}^{-},t\right),v_{i-1,t}^{+}=v\left(x_{i-1}^{+},t\right),$

$z_{i,t}^{-}=z\left(x_i{}^{-},t\right),z_{i-1,t}^{+}=z\left(x_{i-1}^{+},t\right).$

定义 $L_n\left(x\right)$ 为 $n$ 次Legendre多项式。本文中局部基函数的选取方式如下，空间方向上试探基函数为 ${\phi }_0^{(i)}\left(x\right)=\frac{1}{2}\left(L_0\left(\bar{x}\right)-L_1\left(\bar{x}\right)\right),$ ${\phi }_1^{(i)}\left(x\right)=\frac{1}{2}\left(L_0\left(\bar{x}\right)+L_1\left(\bar{x}\right)\right),$ ${\phi }_k^{(i)}\left(x\right)=L_k\left(\bar{x}\right)-L_{k-2}\left(\bar{x}\right),$ $x\in I_i$，其中 $i=1,2,\cdots ,K_1,$ $k=2,3,\cdots ,N_i$。检验基函数为 ${\tilde{\phi }}_n^{(i)}\left(x\right)={\phi }_n^{(i)}\left(x\right),x\in I_i$，其中 $i=1,2,\cdots ,K_1,n=0,1,\cdots ,N_i$。

时间方向上试探基函数为 ${\psi }_0^{(1)}\left(t\right)=1+t,$ ${\psi }_l^{(1)}\left(t\right)=\left(1+t\right)\left(L_l\left(\bar{t}\right)-L_{l+1}\left(\bar{t}\right)\right),$ $t\in J_1$，其中 $l=1,2,\cdots ,M_1-2,$ ${\psi }_0^{(j)}\left(t\right)=\left(1+t\right)\left(1+\left(\bar{t}\right)\right),$ ${\psi }_l^{(j)}\left(t\right)=\left(1+t\right)\left(L_l\left(\bar{t}\right)-L_{l+2}\left(\bar{t}\right)\right),$ $t\in J_j$，其中 $j=2,3,\cdots ,K_2,$ $l=1,2,\cdots ,M_j-3$。检验基函数为 ${\tilde{\psi }}_m^{(j)}\left(t\right)=\left(1-t\right)L_m^{(j)}\left(\bar{t}\right),$ $t\in J_j$，其中 $j=1,2,\cdots ,K_2,$ $m=0,1,\cdots ,M_j-1$。

局部试探基函数为 ${\phi }_k^{(i)}\left(\bar{x}\right){\psi }_l^{(j)}\left(\bar{t}\right)$，局部检验基函数为 ${\tilde{\phi }}_n^{(i)}\left(\bar{x}\right){\tilde{\psi }}_m^{(j)}\left(\bar{t}\right)$，其中 $\left(x,t\right)\in I_i\times J_j,$ $\left(\bar{x},\bar{t}\right)\in \Omega$。

记

$M_1^{(i)}={\left({\tilde{\phi }}_n^{(i)}\left(x\right),{\phi }_k^{(i)}\left(x\right)\right)}_{I_i},M_2^{(j)}={\left({\psi }_l^{(j)}\left(t\right),{\tilde{\psi }}_m^{(j)}\left(t\right)\right)}_{J_j},$

$S_1^{(i)}={\left(\frac{{\tilde{\phi }}_n^{(i)}\left(x\right)}{\partial x},{\phi }_k^{(i)}\left(x\right)\right)}_{I_i},S_2^{(j)}={\left(\frac{{\psi }_l^{(j)}\left(t\right)}{\partial t},{\tilde{\psi }}_m^{(j)}\left(t\right)\right)}_{J_j}.$

$N_1^{(i)}={\left({\tilde{\phi }}_n^{(i)}\left(x\right),L_k^{(i)}\left(x\right)\right)}_{I_i},N_2^{(j)}={\left(L_l^{(j)}\left(t\right),{\tilde{\psi }}_m^{(j)}\left(t\right)\right)}_{J_j}.$

由Legendre多项式的正交性，可计算出以上矩阵中的元素。从而式(6)可转化为如下矩阵方程

$\{\begin{array}{l}{M}_1{U}^{i,j}{S}_2+\sqrt{D}\left[-A_{21}{P}^{i+1,j}{M}_2+A_{11}{P}^{i,j}{M}_2+S_1{P}^{i,j}{M}_1\right]=N_1{F}^{i,j}{N}_2,\hfill \\ M_1{P}^{i,j}{M}_2+\sqrt{D}\left[-A_{22}{U}^{i,j}{M}_2+A_{12}{U}^{i-1,j}{M}_2+S_1{U}^{i,j}{M}_1\right]=0,\hfill \end{array}$ (7)

其中 $F^{i,j}$ 为 $f$ 的系数矩阵，且

$A_{11}={\left({\tilde{\phi }}_n^{(i)}\left(x_{i-1}\right),{\phi }_k^{(i)}\left(x_{i-1}\right)\right)}_{I_i},A_{12}={\left({\tilde{\phi }}_n^{(i)}\left(x_{i-1}\right),{\phi }_k^{(i-1)}\left(x_{i-1}\right)\right)}_{I_i},$

$A_{21}={\left({\tilde{\phi }}_n^{(i)}\left(x_{i-1}\right),{\phi }_k^{(i+1)}\left(x_i\right)\right)}_{I_i},A_{22}={\left({\tilde{\phi }}_n^{(i)}\left(x_i\right),{\phi }_k^{(i)}\left(x_i\right)\right)}_{I_i}.$

在计算线性问题时，对空间区域的方程联立求解，并利用克罗内克积将其写成标准的 $Au=f$ 代数方程形式。增加空间方向区域个数，求解方法类似。依次在每个 $1\le j\le K_2$ 区域上进行求解，每个时间子区域上的求解过程类似。

以空间二区域时间多区域为例，求解时间区间 $J_j$ 时：

$A=\left[\begin{array}{c}\begin{array}{cccc}{S}_2^T\otimes M_1& O& \sqrt{D}\left[M_2^T\otimes A_{11}+M_2^T\otimes S_1\right]& -\sqrt{D}\left[M_1^T\otimes A_{21}\right]\\ \sqrt{D}\left[-M_2^T\otimes A_{22}+M_2^T\otimes S_1\right]& \sqrt{D}\left[M_2^T\otimes A_{12}\right]& M_2^T\otimes M_1& O\\ O& S_2^T\otimes M_1& -\sqrt{D}\left[M_2^T\otimes A_{21}\right]& \sqrt{D}\left[M_2^T\otimes A_{11}+M_2^T\otimes S_1\right]\\ \sqrt{D}\left[M_2^T\otimes A_{12}\right]& \sqrt{D}\left[-M_2^T\otimes A_{22}+M_2^T\otimes S_1\right]& O& M_2^T\otimes M_1\end{array}\end{array}\right]$

$f={\left[\left(N_2^T\otimes N_1\right)vec\left(F^{1,j}\right),O,\left(N_2^T\otimes N_1\right)vec\left(F^{2,j}\right),O\right]}^T.$ (8)

可得数值解系数矩阵

$u^j={\left[vec\left(U^{1,j}\right),vec\left(U^{2,j}\right),vec\left(P^{1,j}\right),vec\left(P^{2,j}\right)\right]}^T,$

在T时刻，方程解由下式给出

$u^{(i,K_2)}\left(x,T\right)={\displaystyle \underset{j=1}{\overset{K_2}{\sum }}{u}^{(i,j)}}\left(x,b_j\right)+U_0^{(i)}\left(x\right).$

该方法也适用于非线性问题，考虑如下形式的一维非线性反应扩散方程

$\begin{array}{l}{\partial }_{t}U-D{\partial }_x^{2}U+G\left(U\right)=f\left(x,t\right),\hfill \end{array}\left(x,t\right)\in \Omega =I_x\times J_t,$ (9)

初始值为 $U\left(x,-1\right)=U_0\left(x\right)$， $x\in I_x$。其中 $G\left(U\right)$ 是关于 $U$ 的非线性项，并考虑周期边界条件。类似求解线性问题的过程，首先引入中间变量 $P=\sqrt{D}{U}_x$ 改写方程为

$\{\begin{array}{l}{\partial }_{t}U-\sqrt{D}\left(P_x\right)+G\left(U\right)=f,\hfill \\ P=\sqrt{D}{U}_x.\hfill \end{array}$ (10)

式(10)的空间LDG谱元法时间Legendre Dual-Petrov-Galerkin谱元法的全离散格式为：寻找 $u,p\in V_N\otimes S_M$ 使得对任意的 $v,z\in V_N\otimes S_M^{*}，$ 有

$\{\begin{array}{l}{\left({\partial }_{t}u,v\right)}_{I_i\times J_j}+\sqrt{D}\left[-{\displaystyle {\int }_{J_j}{\left(\hat{p}\cdot v^{-}\right)}_{i,t}}\text{d}t+{\displaystyle {\int }_{J_j}{\left(\hat{p}\cdot v^{+}\right)}_{i-1,t}}\text{d}t+{\left(p,w_x\right)}_{I_i\times J_j}\right]+{\left({\displaystyle {\prod }_{N_i,M_j}^{C}G,v}\right)}_{I_i\times J_j}={\left(f,v\right)}_{I_i\times J_j},\hfill \\ {\left(p,z\right)}_{I_i\times J_j}+\sqrt{D}\left[-{\displaystyle {\int }_{J_j}{\left(\hat{u}\cdot z^{-}\right)}_{i,t}}\text{d}t+{\displaystyle {\int }_{J_j}{\left(\hat{u}\cdot z^{+}\right)}_{i-1,t}}\text{d}t+{\left(u,z_x\right)}_{I_i\times J_j}\right]=0,\hfill \end{array}$ (11)

其中“ $\stackrel{^}{}$ ”是所选取交替形式的数值流通量。对于非线性项，采用CGL插值进行处理。

以下简明的描述了求解非线性问题的算法。在求解非线性问题的过程中，对于非线性项的处理至关重要。结合迭代法求解，使用上一次迭代所获得的值代入非线性项 $G$，在下一次迭代中使用。类似线性多区域的计算方式，可以将其重写为以下格式。当求解第 $k+1$ 次迭代时形如 $A^{[k+1]}{u}^{[k+1]}=f^{[k+1]}-g\left(u^{[k]}\right),$ 其中

$g={\left[\left(N_2^T\otimes N_1\right)vec\left(G{\left(u^{[k]}\right)}^{1,j}\right),O,\left(N_2^T\otimes N_1\right)vec\left(G{\left(u^{[k]}\right)}^{2,j}\right),O\right]}^T,$

将已得的 $u^{[k]}$ 代入非线性项。然后可以通过Chebyshev-Gauss-Lobatto插值得到系数矩阵。使用 $u^{[0]}$ 为初始迭代值，我们可以从 $A^{[1]}{u}^{[1]}=f^{[1]}-g\left(u^{[0]}\right)$ 中得到第一个迭代值 $u^{[1]}$，依次进行迭代计算。将插值结果 $u^{(i,j-1)}\left(x,b_{j-1}\right)$ 作为时间方向第 $j$ 小区域迭代的初始值。

根据函数的性质，设置迭代的终止条件 $\epsilon$ 和最大迭代次数。当 ${\Vert u^{[k+1]}-u^{[k]}\Vert }_{L^2}\le \epsilon$ 或者小区域迭代次数flag大于所设置的最大值时，本次时间小区域内的迭代计算结束。

4. 收敛性分析

接下来，考虑时空谱元方法全离散格式(6)的收敛性。

定理4.1令 $\left(U,P\right)$ 和 $\left(u,p\right)$ 分别是式(5)和式(6)的解，假设 $\sigma \ge 2,s\ge 1,$ 且 $U\in H_{{\omega }_{0,-1}}^s\left(J_t;H^{\sigma }\left(I_x\right)\right)\cap {\hat{H}}^1\left(J_t;H^{\sigma }\left(I_x\right)\right)\cap L_{{\omega }_{1,-1}}^2\left(J_t;H^{\sigma }\left(I_x\right)\right)$。那么存在正常数 $C$，有

$\begin{array}{l}{\Vert U-u\Vert }_{{\omega }_{0,-1}}^2+{\Vert {\partial }_x\left(U-u\right)\Vert }_{{\omega }_{1,-1}}^2\\ \le C\left[{\hslash }_x^{2\sigma }\left({\left|U\right|}_{\sigma ,{\omega }_{0,-1}}^2+{\left|{\partial }_{t}U\right|}_{\sigma ,{\omega }_{1,-1}}^2\right)+{\hslash }_x^{2(\sigma -1)}{\left|U\right|}_{\sigma -1,{\omega }_{0,-1}}^2+h_t^{-2}{\hslash }_t^{2s}\left({\Vert {\partial }_t^{s}U\Vert }^2+{\Vert {\partial }_t^s{\partial }_{x}U\Vert }^2\right)\right].\end{array}$ (12)

证明由(5)和(6)，可以得到以下方程

$B_{i,j}{\left(U-u,P-p;v,z\right)}_{I_i\times J_j}=0,\forall v,z\in V_N\otimes S_M^{*}$， (13)

其中

$\begin{array}{c}{B}_{i,j}{\left(U-u,P-p;v,z\right)}_{I_i\times J_j}\\ ={\left({\partial }_t\left(U-u\right),v\right)}_{I_i\times J_j}+{\left(P-p,z\right)}_{I_i\times J_j}\\ +\sqrt{D}[{\left(P-p,v_x\right)}_{I_i\times J_j}+{\left(U-u,z_x\right)}_{I_i\times J_j}-{\displaystyle {\int }_{J_j}{\left(\left(P-\hat{p}\right)w^{-}\right)}_{i,t}}\text{d}t\\ +{{\displaystyle {\int }_{J_j}\left(\left(P-\hat{p}\right)w^{+}\right)}}_{i-1,t}\text{d}t-{\displaystyle {\int }_{J_j}{\left(\left(U-\hat{u}\right)z^{-}\right)}_{i,t}}\text{d}t+{\displaystyle {\int }_{J_j}{\left(\left(U-\hat{u}\right)z^{+}\right)}_{i-1,t}}\text{d}t].\end{array}$

令 $U^{*}={\mathcal{P}}_N^{-}{P}_M^{0,-1}U$， $P^{*}={\mathcal{P}}_N^{+}{P}_M^{0,-1}P$。定义

$\begin{array}{l}U-u=\left(U^{*}-u\right)-\left(U^{*}-U\right)=a-a^e,\hfill \\ P-p=\left(P^{*}-p\right)-\left(P^{*}-P\right)=b-b^e.\hfill \end{array}$ (14)

方程可重写为

$B_{i,j}\left(a,b;v,z\right)=B_{i,j}\left(a^e,b^e;v,z\right).$ (15)

首先，令 $v={\omega }_{1,-1}a$， $z={\omega }_{1,-1}b$ 考虑以上方程的左边项

$\begin{array}{l}{B}_{i,j}\left(a,b;{\omega }_{1,-1}a,{\omega }_{1,-1}b\right)\\ ={\left({\partial }_{t}a,a\right)}_{I_i\times J_j,{\omega }_{1,-1}}+{\left(b,b\right)}_{I_i\times J_j,{\omega }_{1,-1}}\\ +\sqrt{D}[{\left(b,a_x\right)}_{I_i\times J_j,{\omega }_{1,-1}}+{\left(a,b_x\right)}_{I_i\times J_j,{\omega }_{1,-1}}-{\displaystyle {\int }_{J_j}{\left(\hat{b}\cdot {\omega }_{1,-1}{a}^{-}\right)}_{i,t}}\text{d}t\\ +{\displaystyle {\int }_{J_j}{\left(\hat{b}\cdot {\omega }_{1,-1}{a}^{+}\right)}_{i-1,t}}\text{d}t-{\displaystyle {\int }_{J_j}{\left(\hat{a}\cdot {\omega }_{1,-1}{b}^{-}\right)}_{i,t}}\text{d}t+{\displaystyle {\int }_{J_j}{\left(\hat{a}\cdot {\omega }_{1,-1}{b}^{+}\right)}_{i-1,t}}\text{d}t].\end{array}$ (16)

根据所设置的交替形式的数值流通量并进行分部积分，可以得到

$\begin{array}{c}{B}_{i,j}\left(a,b;{\omega }_{1,-1}a,{\omega }_{1,-1}b\right)={\left({\partial }_{t}a,a\right)}_{I_i\times J_j,{\omega }_{1,-1}}+{\left(b,b\right)}_{I_i\times J_j,{\omega }_{1,-1}}\\ +\sqrt{D}\left[-{\displaystyle {\int }_{J_j}{\left(\hat{b}\cdot {\omega }_{1,-1}{a}^{-}\right)}_{i,t}}\text{d}t+{\displaystyle {\int }_{J_j}{\left(\hat{a}\cdot {\omega }_{1,-1}{b}^{+}\right)}_{i-1,t}}\text{d}t\right].\end{array}$

对以上方程的所有小区域 $I_i\times J_j$， $i=1,2,\cdots ,K_1$， $j=1,2,\cdots ,K_2$ 求和并由周期边界条件，可以得到

${\displaystyle \underset{i=1}{\overset{K_1}{\sum }}{\displaystyle \underset{j=1}{\overset{K_2}{\sum }}{B}_{i,j}}}\left(a,b;{\omega }_{1,-1}a,{\omega }_{1,-1}b\right)={\left({\partial }_{t}a,a\right)}_{{\omega }_{1,-1}}+{\left(b,b\right)}_{{\omega }_{1,-1}}.$ (17)

接下来，我们考虑式(15)的右端项。可以将其重写为以下形式

$B_{i,j}\left(a^e,b^e;{\omega }_{1,-1}a,{\omega }_{1,-1}b\right)={\left({\partial }_t{a}^e,a\right)}_{I_i\times J_j,{\omega }_{1,-1}}+{\left(b^e,b\right)}_{I_i\times J_j,{\omega }_{1,-1}}+\sqrt{D}\left[{\left(g_1,{\omega }_{1,-1}a\right)}_{I_i\times J_j}+{\left(g_2,{\omega }_{1,-1}b\right)}_{I_i\times J_j}\right],$ (18)

其中

$\begin{array}{c}{\left(g_1,a\right)}_{I_i\times J_j,{\omega }_{1,-1}}={\left(b^e,a_x\right)}_{I_i\times J_j,{\omega }_{1,-1}}-{\displaystyle {\int }_{J_j}{\left({\left(b^e\right)}^{+},{\omega }_{1,-1}{a}^{-}\right)}_{i,t}}\text{d}t+{\displaystyle {\int }_{J_j}{\left({\left(b^e\right)}^{+},{\omega }_{1,-1}{a}^{+}\right)}_{i-1,t}}\text{d}t\\ \le C{\left(g_1,a\right)}_{I_i\times J_j,{\omega }_{0,-1}},\\ {\left(g_2,b\right)}_{I_i\times J_j,{\omega }_{1,-1}}={\left(a^e,b_x\right)}_{I_i\times J_j,{\omega }_{1,-1}}-{\displaystyle {\int }_{J_j}{\left({\left(a^e\right)}^{-},{\omega }_{1,-1}{b}^{-}\right)}_{i,t}}\text{d}t+{\displaystyle {\int }_{J_j}{\left({\left(a^e\right)}^{-},{\omega }_{1,-1}{b}^{+}\right)}_{i-1,t}}\text{d}t\\ \le C{\left(g_2,b\right)}_{I_i\times J_j,{\omega }_{0,-1}},\end{array}$ (19)

$C$ 是一个正常数。根据时间方向上投影算子的性质，有

$\begin{array}{c}{\left(g_1,a\right)}_{I_i\times J_j,{\omega }_{0,-1}}=-{\left(P-{\mathcal{P}}_N^{+}P,a_x\right)}_{I_i\times J_j,{\omega }_{0,-1}}\\ +{\displaystyle {\int }_{J_j}{\left({\left(P-{\mathcal{P}}_N^{+}P\right)}^{+},{\omega }_{0,-1}{a}^{-}\right)}_{i,t}}\text{d}t-{\displaystyle {\int }_{J_j}{\left({\left(P-{\mathcal{P}}_N^{+}P\right)}^{+},{\omega }_{0,-1}{a}^{+}\right)}_{i-1,t}}\text{d}t,\end{array}$

$\begin{array}{c}{\left(g_2,b\right)}_{I_i\times J_j,{\omega }_{0,-1}}=-{\left(U-{\mathcal{P}}_N^{-}U,b_x\right)}_{I_i\times J_j,{\omega }_{0,-1}}\\ +{\displaystyle {\int }_{J_j}{\left({\left(U-{\mathcal{P}}_N^{-}U\right)}^{-},{\omega }_{0,-1}{b}^{-}\right)}_{i,t}}\text{d}t-{\displaystyle {\int }_{J_j}{\left({\left(U-{\mathcal{P}}_N^{-}U\right)}^{-},{\omega }_{0,-1}{b}^{+}\right)}_{i-1,t}}\text{d}t.\end{array}$

引入算子 $\mathcal{D}$，并对上式所有子区域求和。可重写为

${\left(g_1,a\right)}_{{\omega }_{0,-1}}=\mathcal{D}\left(P-{\mathcal{P}}_N^{+}P,{\omega }_{0,-1}a;{\left(P-{\mathcal{P}}_N^{+}P\right)}^{+}\right),$

${\left(g_2,b\right)}_{{\omega }_{0,-1}}=\mathcal{D}\left(U-{\mathcal{P}}_N^{-}U,{\omega }_{0,-1}b;{\left(U-{\mathcal{P}}_N^{-}U\right)}^{-}\right).$

根据引理2.3，可知式(15)的右端项可以重写为

$\begin{array}{l}{\displaystyle \underset{i=1}{\overset{K_1}{\sum }}{\displaystyle \underset{j=1}{\overset{K_2}{\sum }}{B}_{i,j}}}\left(a^e,b^e;{\omega }_{1,-1}a,{\omega }_{1,-1}b\right)={\left({\partial }_t{a}^e,a\right)}_{{\omega }_{1,-1}}+{\left(b^e,b\right)}_{{\omega }_{1,-1}}.\hfill \end{array}$ (20)

因此，由式(15)可以得到以下方程

$\begin{array}{c}{\left({\partial }_{t}a,a\right)}_{{\omega }_{1,-1}}+{\left(b,b\right)}_{{\omega }_{1,-1}}={\left({\partial }_t{a}^e,a\right)}_{{\omega }_{1,-1}}+{\left(b^e,b\right)}_{{\omega }_{1,-1}}\\ ={\left({\partial }_t\left({\mathcal{P}}_N^{-}U-U\right),U^{*}-u\right)}_{{\omega }_{1,-1}}+{\left(P^{*}-P,P^{*}-p\right)}_{{\omega }_{1,-1}}.\end{array}$ (21)

由Cauchy-Schwarz不等式，有

${\Vert U^{*}-u\Vert }_{{\omega }_{0,-2}}^2+{\Vert P^{*}-p\Vert }_{{\omega }_{1,-1}}^2\le C\left({\Vert {\partial }_t\left({\mathcal{P}}_N^{-}U-U\right)\Vert }_{{\omega }_{1,-1}}^2+{\Vert P^{*}-P\Vert }_{{\omega }_{1,-1}}^2\right).$ (22)

根据三角不等式，可得

${\Vert U-u\Vert }_{{\omega }_{0,-1}}^2+{\Vert P-p\Vert }_{{\omega }_{1,-1}}^2\le C\left({\Vert U^{*}-U\Vert }_{{\omega }_{0,-1}}^2+{\Vert P^{*}-P\Vert }_{{\omega }_{0,-1}}^2+{\Vert {\partial }_t\left({\mathcal{P}}_N^{-}U-U\right)\Vert }_{{\omega }_{1,-1}}^2\right).$ (23)

由引理2.1， $N={\min }_{1\le k\le K}{N}_k$ 及 ${\hslash }_x$ 的定义，得到估计

$\begin{array}{c}\Vert {\omega }^e\Vert \le C{h}^{\sigma }{\left(\frac{\Gamma \left(N+2-\sigma \right)}{\Gamma \left(N+2+\sigma \right)}\right)}^{\frac{1}{2}}{\left|u\right|}_{\sigma }\le C{h}^{\sigma }{\left(\frac{1}{{\left(N\right)}^{2\sigma }}\right)}^{\frac{1}{2}}{\left|u\right|}_{\sigma }\\ \le C{\hslash }_x^{\sigma }{\left|u\right|}_{\sigma }.\end{array}$

由引理2.2，其中 $l=0$，可以得到以下估计结果

$\begin{array}{c}{\Vert U^{*}-U\Vert }_{{\omega }_{0,-1}}={\Vert {\mathcal{P}}_N^{-}{P}_M^{0,-1}U-U\Vert }_{{\omega }_{0,-1}}\\ ={\Vert -\left(I-{\mathcal{P}}_N^{-}\right)U+\left(I-{\mathcal{P}}_N^{-}\right)\left(I-P_M^{0,-1}\right)U-\left(I-P_M^{0,-1}\right)U\Vert }_{{\omega }_{0,-1}}\\ \le C\left({\Vert \left(I-{\mathcal{P}}_N^{-}\right)U\Vert }_{{\omega }_{0,-1}}+{\Vert \left(I-P_M^{0,-1}\right)U\Vert }_{{\omega }_{0,-1}}\right)\\ \le C\left({\hslash }_x^{\sigma }{\left|U\right|}_{\sigma ,{\omega }_{0,-1}}+h_t^{-1}{\hslash }_t^s\Vert {\partial }_t^{s}U\Vert \right),\end{array}$ (24)

$\begin{array}{c}{\Vert P^{*}-P\Vert }_{{\omega }_{0,-1}}={\Vert {\mathcal{P}}_N^{+}{P}_M^{0,-1}P-P\Vert }_{{\omega }_{0,-1}}\\ ={\Vert -\left(I-{\mathcal{P}}_N^{+}\right)P+\left(I-{\mathcal{P}}_N^{+}\right)\left(I-P_M^{0,-1}\right)P-\left(I-P_M^{0,-1}\right)P\Vert }_{{\omega }_{0,-1}}\\ \le C\left({\Vert \left(I-{\mathcal{P}}_N^{+}\right){\partial }_{x}U\Vert }_{{\omega }_{0,-1}}+{\Vert \left(I-P_M^{0,-1}\right){\partial }_{x}U\Vert }_{{\omega }_{0,-1}}\right)\\ \le C\left({\hslash }_x^{\sigma -1}{\left|U\right|}_{\sigma -1,{\omega }_{0,-1}}+h_t^{-1}{\hslash }_t^s\Vert {\partial }_t^s{\partial }_{x}U\Vert \right),\end{array}$ (25)

$\begin{array}{l}{\Vert {\partial }_t\left({\mathcal{P}}_N^{-}U-U\right)\Vert }_{{\omega }_{1,-1}}\le C{\hslash }_x^{\sigma }{\left|{\partial }_{t}U\right|}_{\sigma ,{\omega }_{1,-1}}.\hfill \end{array}$ (26)

至此，全离散格式的收敛性得以证明。

5. 数值算例

在本节中，分别给出了线性和非线性问题求解所得的 $L^2$ 误差，验证了该时空谱方法的有效性和精确性。对于部分数值算例，提供了本文方法所得的数值结果与相同条件下其他研究方法所得结果的对比。

例1. 考虑如下一维线性问题

$\begin{array}{ll}{u}_t=u_{xx},\hfill & \left(x,t\right)\in \left(0,2\pi \right)\times \left(0,1\right],\hfill \\ u\left(x,0\right)=\sin \left(x\right),\hfill & x\in \left(0,2\pi \right),\hfill \end{array}$

精确解为 $u\left(x,t\right)={\text{e}}^{-t}\sin \left(x\right)$。相应的数值结果在表1给出。表2中列出了文献 [20] 中对此示例求解所得的 $L^2$ 误差。

Table 1. The L2-error for Example 1 with two-interval method in space

表1. 例1空间二区域数值结果L²误差

Table 2. The error result of reference [20] at Radau points at T = 1

表2. 文献 [20] 在 Radau点上的误差结果 T = 1

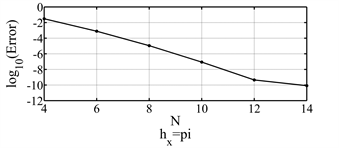(a) spatial (b) time

Figure 1. The convergence rate of method (6) when K_x = 2, K_t = 4

图1. K_x = 2，K_t = 4时方法(6)的收敛情况

采用空间LDG谱元法，时间谱元法求解以上方程。在空间方向上剖分为二区域，N表示每个子区域的多项式次数，在时间方向上剖分为四区域，M表示每个子区域的多项式次数。在表2中，列出了在空间上采用LDG有限元法，时间上采用Runge-kutta离散 [20] 所得的L²误差。表2中N₁为文献中空间方向剖分个数， $\Delta t$ 为时间方向Runge-kutta步长。数值结果表明，本文方法在对于此问题的求解具有良好的精度。当固定时间方向上多项式次数M = 8，取不同的N时得到图1中子图(a)。当固定空间方向上多项式次数N = 14，取不同的M时得到图1中子图(b)。更直观的给出了剖分方式为K_x = 2，K_t = 4时的数值结果。

例2. 考虑时间区间为(0, 8]的如下问题

$\begin{array}{ll}{u}_t=u_{xx}-u+{\pi }^2{e}^{-t}\cos \left(\pi x\right),\hfill & \left(x,t\right)\in \left(-1,1\right)\times \left(0,8\right],\hfill \\ u\left(x,0\right)=\cos \left(\pi x\right),\hfill & x\in \left(-1,1\right),\hfill \end{array}$

精确解为 $u\left(x,t\right)={\text{e}}^{-t}\cos \left(\pi x\right)$。表3和表4中给出了使用本文方法(6)的求解结果。表5中的结果是由 [32] 所提出的。

Table 3. L2-error at T = 8 for Example 2 with two-interval method in space

表3. 例2空间二区域在T = 8时的数值结果L²误差

Table 4. L2-error at T = 8 for Example 2 with four-interval method in space

表4. 例2空间四区域在T = 8时的数值结果L²误差

Table 5. Results in [32] at T = 8

表5. 文献 [32] 的数值结果T = 8

从表3和表4验证，可以通过增加子区域个数或者多项式的阶数来获得更高精度的数值结果。表5中的结果在文献 [32] 中给出，是采用DG有限元法和Strang对称算子相结合的方法求解示例2所得到的。表5中N₁是空间子区域的划分数，M₁是时间步长。由此可得，本文方法具有较高的准确性。并且对于较大的时间区间问题该方法也是有效且高精度的。

例3. 考虑如下线性间断问题

$u_t-u_{xx}=\{\begin{array}{l}2\left(2{\pi }^2+1\right){\text{e}}^{2t}\sin \left(2\pi x\right),\left(x,t\right)\in \left(-1,0\right)\times \left(-1,1\right],\hfill \\ 2\left(2{\pi }^2+1\right){\text{e}}^{2t}\cos \left(2\pi x\right),\left(x,t\right)\in \left(0,1\right)\times \left(-1,1\right],\hfill \end{array}$

有精确解

$u\left(x,t\right)=\{\begin{array}{l}{\text{e}}^{2t}\sin \left(2\pi x\right),\left(x,t\right)\in \left(-1,0\right)\times \left(-1,1\right],\hfill \\ {\text{e}}^{2t}\cos \left(2\pi x\right),\left(x,t\right)\in \left(0,1\right)\times \left(-1,1\right].\hfill \end{array}$

Table 6. The L2-error for Example 3

表6. 例3的数值结果L²误差

在求解过程中，将空间区间剖分为四区域并将时间区间剖分为四区域。在表6中，N是每个空间子区域上的多项式次数，M是每个时间子区域上的多项式次数。结果显示所提出的时间谱元空间局部间断Galerkin谱元方法对于该间断问题的处理是有效的。

接下来，应用方法(11)求解非线性反应扩散问题。

例4. 考虑如下非线性问题

$\begin{array}{ll}{u}_t+{\left(0.5u^2\right)}_x=0.5u_{xx}+0.5{\text{e}}^{-t}\sin \left(2x\right),\hfill & \left(x,t\right)\in \left(-\pi ,\pi \right)\times \left(0,T\right],\hfill \\ u\left(x,0\right)=\sin \left(x\right),\hfill & x\in \left(-\pi ,\pi \right),\hfill \end{array}$

精确解为 $u\left(x,t\right)={\text{e}}^{-0.5t}\sin \left(x\right)$。如表7中给出了应用第三节中描述的非线性问题算法对例4的 $T=1$ 和 $T=0.5$ 两种情况分别求解所得结果。表8中给出了文献 [33] 对应情况下的数值结果。

Table 7. The L2-error for Example 4 with two-interval method in space

表7. 例4空间二区域在T = 8时的数值结果L²误差

推广至一维非线性反应扩散问题，其中非线性项采用CGL插值进行处理。结合迭代法进行求解，当L²范数下两次迭代差值小于10⁻¹²或迭代次数大于20时，本次迭代结束。表7中给出了应用本文方法所得的L²误差。

Table 8. The L2-error in [33]

表8. 文献 [33] 的数值结果L²误差

在表8中，列出了 [33] 在空间上采用LDG方法，时间上采用Runge-kutta方法离散所得的 $L^2$ 误差。其中 $N_1$ 为文献中空间方向的剖分个数， $\Delta t$ 为时间方向Runge-kutta的步长。数值结果表明，本文方法在求解非线性问题时可获得良好的精度。

6. 总结

本文提出了一维线性反应扩散方程的空间LDG时间Legendre dual-Petrov-Galerkin谱元法。在每个空间子区域上按Legendre-Galerkin谱方法生成格式，边界处跳跃项由交替形式的数值流通量处理。在时间方向上选择满足双重边界条件的试探函数和检验函数，借助对偶的思想形成谱元法的数值格式。本文给出了对线性方程的算法描述及全离散格式的收敛性分析。并将其推广应用至非线性反应扩散方程的数值计算中，结合迭代法给出算法描述，其中非线性项采用CGL点上的插值进行处理。多区域数值结果显示本文方法在对于线性及非线性问题的应用中都具有良好的精度。接下来，可以考虑对非线性问题的分析及二维反应扩散方程的应用。

基金项目

国家自然科学基金(No. 11971016)。