考虑锅炉效率不确定的蒸汽动力系统鲁棒优化设计

Robust Optimal Design of Steam Power System Considering the Uncertainty of Boiler Efficiency

摘要: 锅炉效率在蒸汽动力系统运行过程中存在波动，为保证系统的高效安全运行，本文研究锅炉效率不确定情况下的蒸汽动力系统鲁棒优化问题。本研究基于一种数据驱动的自适应鲁棒优化方法，利用工业已有数据样本，通过鲁棒核密度估计构建锅炉效率不确定集合，降低了鲁棒优化问题的保守性，再结合混合整数线性规划(MILP)模型，建立自适应鲁棒混合整数线性规划模型。优化模型以蒸汽动力系统的总运行成本最小为目标函数，决策变量包括描述蒸汽轮机选型的整数变量和表征系统蒸汽分布情况的连续变量。应用实例表明，与确定性方法相比，鲁棒优化得到的最优操作策略，鲁棒优化在理想效率下总成本增加约24.00%，在低效率下总成本降低约12.17%，对于系统的鲁棒性上提高了15.14%，鲁棒生产超高压蒸汽，可以随需求转换为其他等级蒸汽，系统工作状态受到外界因素影响小，在锅炉效率存在波动的情况下，结果更加具有经济性。

Abstract: The boiler efficiency fluctuates during the operation of the steam power system. In order to ensure the efficient and safe operation of the system, this paper studies the robust optimization of the steam power system when the boiler efficiency is uncertain. This research is based on a data-driven adaptive robust optimization method, using existing industrial data samples to construct a boiler efficiency uncertainty set through robust kernel density estimation, reducing the conservativeness of the robust optimization problem, and combining it with mixed integer linearity Planning (MILP) model to establish an adaptive robust mixed integer linear programming model. The optimization model takes the minimum total operating cost of the steam power system as the objective function. The decision variables include integer variables that describe the selection of steam turbines and continuous variables that characterize the steam distribution of the system. Application examples show that, compared with the deterministic method, the optimal operation strategy obtained by robust optimization, the total cost of robust optimization increases by about 24.00% under ideal efficiency, and the total cost is reduced by approximately 12.17% under low efficiency, which is very effective for the robustness of the system. The robustness has been increased by 15.14%. The robust production of ultra-high-pressure steam can be converted to other grades of steam as required. The working state of the system is less affected by external factors. In the case of fluctuations in boiler efficiency, the result is more economical.

1. 引言

蒸汽动力系统作为供能系统，是工业生产中重要系统之一 [1] [2]，当人们想要最大化或最小化某一特定目标时，就不可避免要分析整体系统和优化问题。蒸汽动力系统在实现能源转换的工程中会造成大量的环境污染和能源消耗，整个转换过程中设备有锅炉、换热网络、汽轮机等。蒸汽动力系统中存在许多不确定因素，例如伴随燃料价格、电价、生产量、季节变化等原因，导致产品设备的选型和各个专业器械的配置变化；制定的生产计划和外在条件的变化，导致整个系统的生产变化。不确定因素影响着蒸汽动力系统的优化，直接使用确定条件进行优化，受不确定因素影响可能使整个优化方案不是实际最优解。把不确定因素考虑到优化模型中，可以增加系统柔性，更能稳定的降低系统经济成本，提高系统的综合性能。

Papalexandri [3] 将汽轮机效率作为不确定因素，通过不同周期设备转换所产生费用对总运行费用的影响，建立了多周期运行成本的优化模型。Aguilar等 [4] 将汽电需求作为确定性周期因素，燃料和电力价格作为不确定因素，建立蒸汽动力系统优化模型。张冰剑等 [5] 建立了以设备出现故障所导致的维护时间为不确定因素建立了多目标优化模型。罗向龙等 [6] 将运行过程以8个小时为一个固定周期，对蒸汽动力系统进行多周期优化分析。此后罗向龙等将蒸汽动力系统的不稳定因素，汽电需求的改变引入模型，整个系统的运行过程被分成等间隔的多周期过程。李晖等 [7] 将汽电需求转变为周期性确定变化，使用多周期进行描述，对不同的波动影响因素采用不同的权重来描述在多周期过程中的影响信息。池晓等 [8] 用蒸汽需求量作为不确定因素，在蒸汽需求量的概率范围内离散化转换为确定性的多周期优化过程。Ran等 [9] 把约束描述的不确定因素进行简化，建立了针对蒸汽动力系统的鲁棒优化模型，并且通过实例证明有效性和鲁棒性。Rami等 [10] 对一种带有蒸汽轮机的电力系统负载频率控制器进行优化，建立复杂的多项式约束来达到系统要求，并且尽可能精确描述系统的运行模式，通过鲁棒优化模型的实例证明，在系统稳定的前提下，系统响应时间得到了优化。彭春华等 [11] 针对光伏电站系统的经济性和可靠性建立优化模型，使用盒式不确定集合对于光伏生产进行估计，并在鲁棒优化模型中加入不确定预算，来调节盒式不确定集合对于不确定因素估计太保守的问题。Zhao等 [12] 研究使用数据驱动自适应鲁棒优化方法，把蒸汽动力系统中汽轮机效率不确定性作为不确定参数，通过历史数据推倒汽轮机模型，使用鲁棒核密度估计构造不确定集合，通过仿射决策原则，将多级优化模型转化为鲁棒优化模型，把模型应用到某乙烯装置的蒸汽系统，证明模型的适用性。Akbari等 [13] 提出了一种新的鲁棒输出反馈控制器来调节非线性锅炉–汽轮机系统的输出功率。在实际数据的基础上，围绕实际工作点对系统进行线性化处理，确定了不确定项的实际取值范围。Shen等 [14] 将汽轮机进气的焓和出气的焓考虑为不确定参数，把确定性优化模型转化为混合整数非线性规划问题，根据机理和历史数据建立模型，在确定性模型中代入不确定集合，建立一种数据驱动的鲁棒优化模型。Paepe等 [15] 对微型燃气轮机的设计进行鲁棒设计，用鲁棒优化描述运行参数和设计参数的不确定性，优化了微型燃气轮机转速和电效率。

上述文献主要针对汽电需求的变化转为周期性确定变化和汽轮机效率不确定因素对于蒸汽动力系统的影响，在一定程度上是一种改进。但在蒸汽动力系统中锅炉效率不确定性变化实时存在，影响着蒸汽动力系统生产的稳定性和安全性，不过因锅炉效率不确定范围在1以内，相对于其他不确定因素数值偏小，不能转化为多周期性问题，需要结合鲁棒优化进行优化设计。

锅炉效率主要因素如图1所示，包括烟气容积及排烟温度，可燃气体不完全燃烧引起的热损失，飞灰、炉渣和灰渣的含碳量，锅炉外表面积大小、炉墙结构、保温性能、环境温度和锅炉额定蒸发量，炉渣、粉煤灰沉降灰分含量和灰分温度。锅炉效率受多种因素共同影响，难以使用确定方程准确计算，所以采用不确定集合来描述锅炉效率才能更贴近实际。

Figure 1. Uncertainty factors of boiler

图1. 锅炉不确定性因素

因此本文通过对蒸汽动力系统的不确定性因素进行分析，以锅炉效率为不确定性因素，利用系统运行产生的历史数据，采用鲁棒核密度估计方法，得到不确定集合，基于混合整数线性规划(MILP)方法，建立以系统经济指标为目标函数的自适应鲁棒优化混合整数线性规划模型。

2. 问题描述及系统建模

2.1. 问题描述

考虑如图2所示的过程工业广泛应用的蒸汽动力系统 [12] [13] [14]，该系统分为超高(SS)、高(HS)、中(MS)、低压(LS)、冷凝水(SC)五个等级，不同等级的管网之间安装汽轮机，汽轮机做功产生计划生产的电力和动力，假使系统的发电量不满足计划，也可以使用国家电网买电。不同等级的蒸汽量可以通过减温减压器来进行调节，使得不同等级的蒸汽满足需求，也不会出现过多的情况。

超结构模型需要包括所有系统可以产生的方案，理论上每一个等级的蒸汽都能由锅炉、余热锅炉生产，每种等级的蒸汽之间都应有蒸汽透平：包括单级背压透平、冷凝透平、多级抽汽透平，超结构模型的设备和结构都足够复杂。在有针对性的设计超结构模型，要结合经验方法和实际结果，排除不具有可行性的结构方案，通过实际需求来设计各级之间的流量限制和运行设备的负荷，确定具体的结构和设备个数。

Figure 2. Superstructure system

图2. 超结构系统

对系统建立集成模型，主要的方法是出混合整数线性规划(MILP)和混合整数非线性规划(MINLP)这两种模型。其中包括锅炉、汽轮机等系统主要设备的数学模型，分析设备的工作运行原理建立物料平衡和能量平衡等方程，用连续变量表示系统设备进出口的流程，流量，对于设备的启用情况和运行情况用0-1变量表示。

2.2. 确定性优化数学模型

2.2.1. 目标函数

设置经济效益函数为目标函数，包括运行的燃料成本、外购蒸汽成本、生产所需水的成本。

$\min C_{tot}=C_{fuel}{\displaystyle \underset{b}{\sum }{M}_{fuel,b}}+{\displaystyle \underset{sh}{\sum }{C}_{st,sh}^{in}}{M}_{st,sh}^{in}+C_{water}{\displaystyle \underset{lv}{\sum }\left(l_{lv}-1\right)M_{water,lv}}+C_{water}{\displaystyle \underset{sh}{\sum }{M}_{st,sh}^{out}}-{\displaystyle \underset{sh}{\sum }{C}_{st,sh}^{out}}{M}_{st,sh}^{out}$ (1)

其中，C_tot为年度总成本，C_fuel为使用的燃料的单价，M_in,b为锅炉b理想消耗燃料量， $C_{st,sh}^{in}$ 为在sh等级外购蒸汽单价， $M_{st,sh}^{in}$ 为在sh等级所需的外购蒸汽量，C_water为减温减压器中水的单价。

${\displaystyle \underset{lv}{\sum }\left(l_{lv}-1\right)M_{water,lv}}$ 为减温减压器的消耗量，l_lv为减温减压器模型系数 [12]， $l_{lv}=\frac{h_{in,lv}-h_{water,lv}}{h_{out,lv}-h_{water,lv}}$， $C_{st,sh}^{out}$ 为在sh等级外售蒸汽单价， $M_{st,sh}^{out}$ 为在sh等级所需的外售蒸汽量。

2.2.2. 约束条件

1) 蒸汽锅炉效率模型

公式(2)为锅炉效率的经验模型 [14]

$\eta ={\alpha }_b{M}_{water,b}^{in}/M_{st,b}^{\max }+{\beta }_b,\forall b$ (2)

其中， $M_{water,b}^{in}$ 为锅炉产气量， $M_{st,b}^{\max }$ 为锅炉最大产气量， ${\alpha }_b$， ${\beta }_b$ 为回归参数。

2) 锅炉能量平衡方程：

$M_{fuel,b}{Q}_{fuel,b}=M_{st,b}^{out}\left(H_{st,b}^{out}-H_{water,b}^{in}\right),\forall b$ (3)

其中， $Q_{fuel,b}$ 为单位体积燃料输入锅炉的热量， $M_{st,b}^{out}$ 为锅炉出口产气量， $H_{st,b}^{out}$ 为锅炉出口蒸汽的焓值， $H_{water,b}^{in}$ 为锅炉给水的焓值。从式(2)及式(3)可以看出锅炉效率直接影响锅炉进水量和燃料量，对于蒸汽动力系统的成本紧密相关。

3) 质量平衡约束

$M_{t,sl}^{in}{y}_{t,sl}^{in}=M_{t,sl}^{ext}{y}_{t,sl}^{ext}+M_{t,sl}^{out},\forall t$ (4)

其中， $M_{t,sl}^{in}$ 为汽轮机t在sl等级的接口蒸汽量， $y_{t,sl}^{in}$ 为汽轮机t的sl等级的选型函数, $M_{t,sl}^{ext}$ 为汽轮机t在sl等级的抽汽量， $y_{t,sl}^{ext}$ 为汽轮机t在sl等级抽汽的选型函数， $M_{t,sl}^{out}$ 为汽轮机t在sl等级的出口蒸汽量。

4) 各等级蒸汽需求约束

${\displaystyle \underset{b}{\sum }{y}_{sh,b}^{out}{M}_{st,b}^{out}}+{\displaystyle \underset{lv}{\sum }\left(y_{sh}^{in}{}_{,lv}{M}_{water}^{in}{}_{,lv}+y_{sh}^{out}{}_{,lv}{M}_{water}^{out}{}_{,lv}\right)}+{\displaystyle \underset{sh}{\sum }\left(y_{sh}^{in}{M}_{st,sh}-y_{sh}^{out}{M}_{st,sh}^{out}\right)}\ge M_{st,sh}^{dem},\forall sh\in SH$ (5)

其中， $y_{sh,b}^{out}$， $y_{sh}^{in}{}_{,lv}$， $y_{sh,lv}^{out}$， $y_{sh}^{in}$， $y_{sh}^{out}$ 分别为锅炉产汽、减温减压器入口和出口、外购和售出蒸汽等级的在sh等级的选型参数， $M_{st,b}^{out}$ 为锅炉b在sh等级的产汽量， $M_{water}^{in}{}_{,lv}$， $M_{water}^{out}{}_{,lv}$ 分别为减温减压器在sh等级的入口和出口流量， $M_{st,sh}$， $M_{st,sh}^{out}$ 分别为外购和售出的sh等级蒸汽量， $M_{st,sh}^{dem}$ 为运行过程对sh等级蒸汽的需求量。

5) 机械能需求约束

$W_t\ge W{D}_t,\forall t\in T$ (6)

其中， $W_t$ 为汽轮机提供的机械能， $W{D}_t$ 为压缩机或泵的机械工作需求。

6) 变量约束

根据设计和操作条件，该优化模型中的所有变量必须在安全范围内

$M^{\min }\le M\le M^{\max }$ (7)

M表示操作变量的集合，包括锅炉燃料量 $M_{fuel,b}$，锅炉的产气量 $M_{water,b}^{in}$，各等级外购蒸汽量 $M_{st,sh}$，减温减压器消耗量 $\left(l_{lv}-1\right)M_{water,lv}$。

综上，模型为确定性条件下经济函数的蒸汽动力系统优化设计，以式(1)为目标函数，考虑约束条件式(2)~(7)的MILP优化问题。

2.3. 数据驱动的考虑锅炉效率不确定条件的鲁棒优化建模

选用高斯核函数作为鲁棒核密度估计的核函数，并对数据进行鲁棒处理 [11] - [16]，极端值对应的函数值分配极小的权重w_i，得到鲁棒核密度估计函数。

根据不确定量得到的数据建立不确定集合，改善保守度，根据决策者的需要，在不确定集中增加一个不确定预算参数 $\mu$，来进一步调节集合的保守度，以使其在经济性方面的表现更符合决策者的需要。

$U=\left\{r|\begin{array}{l}{\hat{F}}_{RKDE}^{(i)-1}\left(\alpha \right)\le r_i\le {\hat{F}}_{RKDE}^{(i)-1}\left(1-\alpha \right),\forall i\\ {\displaystyle \underset{i}{\sum }{r}_i^0\left(1-{\epsilon }_i\mu \right)}\le {\displaystyle \underset{i}{\sum }{r}_i}\le {\displaystyle \underset{i}{\sum }{r}_i^0\left(1+{\epsilon }_i\mu \right)}\end{array}\right\}$ (8)

其中 $r_i^0=\left({\hat{F}}_{RKDE}^{(i)-1}\left(\alpha \right)+{\hat{F}}_{RKDE}^{(i)-1}\left(1-\alpha \right)\right)/2$ 为中心值， ${\epsilon }_i=\left({\hat{F}}_{RKDE}^{(i)-1}\left(1-\alpha \right)-r_i^0\right)/r_i^0$ 为相应中心值的偏移量。

${\Vert \sigma \left(r-r^0\right)\Vert }_1\le \psi$ (9)

其中， $\sigma ={\Delta }^{-1/2}$，∆是不确定参数的协方差矩阵， $\psi$ 用于调整约束中范数的大小。

$U^{cor}=\left\{r|\begin{array}{l}{\hat{F}}_{RKDE}^{(i)-1}\left(\alpha \right)\le r_i\le {\hat{F}}_{RKDE}^{(i)-1}\left(1-\alpha \right),\forall i\\ {\displaystyle \underset{i}{\sum }{r}_i^0\left(1-{\epsilon }_i\mu \right)}\le {\displaystyle \underset{i}{\sum }{r}_i}\le {\displaystyle \underset{i}{\sum }{r}_i^0\left(1+{\epsilon }_i\mu \right)}\\ {\Vert \sigma \left(r-r^0\right)\Vert }_1\le \psi \end{array}\right\}$ (10)

首先，锅炉效率的不确定参数从历史数据中收集，利用RKDE从不确定参数中构造不确定集式(11)，参照不确定集合常规构造方法 [12]。置信水平为(1-2α)，增大α值意味着置信水平小，减小α值使解更保守。

由于蒸汽动力系统的系数参数存在不确定性，我们将目标函数(1)重新表述为：

$\underset{M}{\min }\underset{r\in u}{\max }{C}_{fuel}{\displaystyle \underset{b}{\sum }{M}_{fuel,b}}+{\displaystyle \underset{sh}{\sum }{C}_{st,sh}^{in}}{M}_{st,sh}+C_{water}{\displaystyle \underset{lv}{\sum }\left(l_{lv}-1\right)M_{water,lv}}+C_{water}{\displaystyle \underset{sh}{\sum }{M}_{st,sh}^{out}}-{\displaystyle \underset{sh}{\sum }{C}_{st,sh}^{out}}{M}_{st,sh}^{out}$ (11)

针对蒸汽动力系统不确定性模型式(8)，其中把含有不确定参数的目标函数其中包含的最大最小问题转化为最小化问题，转换形式如下：

$\begin{array}{l}\underset{M,z}{\min }z\\ \text{s}\text{.t}\text{.}{C}_{fuel}{\displaystyle \underset{b}{\sum }{M}_{fuel,b}}\left(r\right)+{\displaystyle \underset{sh}{\sum }{C}_{st,sh}^{in}}{M}_{st,sh}+C_{water}{\displaystyle \underset{lv}{\sum }\left(l_{lv}-1\right)M_{water,lv}}\\ +C_{water}{\displaystyle \underset{sh}{\sum }{M}_{st,sh}^{out}}-{\displaystyle \underset{sh}{\sum }{C}_{st,sh}^{out}}{M}_{st,sh}^{out}\le z,\forall r\in U^{cor}\end{array}$ (12)

r表示锅炉中的不确定因素，锅炉效率从燃料的种类到燃尽的情况，从烟气的燃烧情况到排出烟气的容积和温度等等因素，都共同影响着锅炉效率 [17]，在多种因素作用下很难得到准确的关系式，所以采用建立不确定集合的方式，使用鲁棒优化算法对锅炉效率影响的目标函数进行求解。

根据不确定参数的数据构建不确定集合，将式(2)用来描述锅炉实际使用的燃料量。

$M_{fuel,b}\left(r\right)=M_{fuel,b}\eta +b_{bias},\forall b,r\in U^{cor}$ (13)

锅炉实际使用的燃料量 $M_{in,b}\left(r\right)$ 范围约束重新表述为：

$M_{fuel,b}^{\min }\le M_{fuel,b}\left(r\right)\le M_{fuel,b}^{\max },\forall b,r\in U^{cor}$ (14)

确定性锅炉能量平衡(3)被重新表述为：

$M_{fuel,b}\left(r\right)Q_{fuel,b}=M_{st,b}^{out}\left(H_{st,b}^{out}-H_{water,b}^{in}\right),\forall b,r\in U^{cor}$ (15)

采用线性对偶理论将目标函数式(12)内部的最大化问题转换为其对偶形式。该式内部优化问题为：

$\begin{array}{l}\underset{r\in U}{\max }{M}_{fuel,b}\left(r\right)C_{fuel}\\ \text{s}\text{.t}\text{.}\{\begin{array}{l}{r}_i\le {\hat{F}}_{RKDE}^{(i)-1}\left(1-\alpha \right),\forall i\\ -r_i\le -{\hat{F}}_{RKDE}^{(i)-1}\left(\alpha \right),\forall i\\ {\displaystyle \underset{i}{\sum }{r}_i}\le {\displaystyle \underset{i}{\sum }{r}_i^0\left(1+{\epsilon }_i\mu \right)}\\ -{\displaystyle \underset{i}{\sum }{r}_i}=-{\displaystyle \underset{i}{\sum }{r}_i^0\left(1-{\epsilon }_i\mu \right)}\end{array}\end{array}$ (16)

根据式(13)将(12)中的约束条件转化为：

$\begin{array}{c}\underset{r\in U^{cor}}{\max }{C}_{fuel}{\displaystyle \underset{b}{\sum }{M}_{fuel,b}\left(r\right)\eta }\le z-{\displaystyle \underset{sh}{\sum }{C}_{st,sh}^{in}}{M}_{st,sh}-C_{water}{\displaystyle \underset{lv}{\sum }\left(l_{lv}-1\right)M_{water,lv}}\\ -C_{water}{\displaystyle \underset{sh}{\sum }{M}_{st,sh}^{out}}+{\displaystyle \underset{sh}{\sum }{C}_{st,sh}^{out}}{M}_{st,sh}^{out}-C_{fuel}{\displaystyle \underset{b}{\sum }{b}_{bias}}\end{array}$ (17)

约束式(10)在实际应用的数据集中建立相应约束条件：

${\displaystyle \underset{k}{\sum }{\theta }_k}\le \psi$ (18)

${\displaystyle \underset{i}{\sum }{\sigma }_{k,i}{r}_i-{\theta }_k}\le r^{cor,sum},\forall k$ (19)

$-{\displaystyle \underset{i}{\sum }{\sigma }_{k,i}{r}_i-{\theta }_k}\le -r^{cor,sum},\forall k$ (20)

$r^{cor,sum}={\displaystyle \underset{i}{\sum }{\sigma }_{k,i}{r}_i^0}$ (21)

式(21)的约束条件为式(18)~(20)。

式(17)对偶形式为：

$\begin{array}{l}{\displaystyle \underset{i}{\sum }{\hat{F}}_{RKDE}^{(i)-1}\left(1-\alpha \right){\chi }_i}-{\displaystyle \underset{i}{\sum }{\hat{F}}_{RKDE}^{(i)-1}\left(\alpha \right){\delta }_i}+\alpha {\displaystyle \underset{i}{\sum }{r}_i^0\left(1+{\epsilon }_i\mu \right)}-\beta {\displaystyle \underset{i}{\sum }{r}_i^0\left(1-{\epsilon }_i\mu \right)}+\psi D1+D{2}_k{r}^{cor,sum}-D{3}_k{r}^{cor,sum}\\ \le z-{\displaystyle \underset{sh}{\sum }{C}_{st,sh}^{in}}{M}_{st,sh}-C_{water}{\displaystyle \underset{lv}{\sum }\left(l_{lv}-1\right)M_{water,lv}}-C_{water}{\displaystyle \underset{sh}{\sum }{M}_{st,sh}^{out}}+{\displaystyle \underset{sh}{\sum }{C}_{st,sh}^{out}}{M}_{st,sh}^{out}-C_{fuel}{\displaystyle \underset{b}{\sum }{b}_{bias}}\end{array}$ (22)

${\chi }_i-{\delta }_i+\alpha -\beta +{\displaystyle \underset{k}{\sum }{\sigma }_{k,i}\cdot D{2}_k}-{\displaystyle \underset{k}{\sum }{\sigma }_{k,i}\cdot D{3}_k}=C_{fuel}{\displaystyle \underset{b}{\sum }{M}_{in,b}\eta },\forall i$ (23)

$D1+D{2}_k-D{3}_k=0,\forall k$ (24)

${\chi }_i,{\delta }_i,\alpha ,\beta ,D1,D{2}_k,D{3}_k\ge 0,\forall i,k$ (25)

其中， ${\chi }_i,{\delta }_i,\alpha ,\beta ,D1,D{2}_k,D{3}_k$ 是相应的对偶变量。

平衡约束(15)的对偶形式为:

$\begin{array}{l}{\displaystyle \underset{i}{\sum }{\hat{F}}_{RKDE}^{(i)-1}\left(1-\alpha \right){\tau }_{b,i}}-{\displaystyle \underset{i}{\sum }{\hat{F}}_{RKDE}^{(i)-1}\left(\alpha \right){\pi }_{b,i}}+{\alpha }_b{\displaystyle \underset{i}{\sum }{r}_i^0\left(1+{\epsilon }_i\mu \right)}-{\beta }_b{\displaystyle \underset{i}{\sum }{r}_i^0\left(1-{\epsilon }_i\mu \right)}+\psi D{4}_b\\ +D{5}_{b,k}{r}^{cor,sum}-D{6}_{b,k}{r}^{cor,sum}=M_{st,b}^{out}\left(H_{st,b}^{out}-H_{water,b}^{in}\right)-b_{bias}{Q}_{fuel,b},\forall b\end{array}$ (26)

${\tau }_{b,i}-{\pi }_{b,i}+{\alpha }_b-{\beta }_b+{\displaystyle \underset{k}{\sum }{\sigma }_{k,i}\cdot D{5}_{b,k}}-{\displaystyle \underset{k}{\sum }{\sigma }_{k,i}\cdot D{6}_{b,k}}=Q_{fuel,b}{\displaystyle \underset{b}{\sum }{M}_{fuel,b}\eta },\forall i,b$ (27)

$D{4}_b+D{5}_{b,k}-D{6}_{b,k}=0,\forall b,k$ (28)

${\tau }_{b,i},{\pi }_{b,i},{\alpha }_b,{\beta }_b,D{4}_b,D{5}_{b,k},D{6}_{b,k}\ge 0,\forall i,b,k$ (29)

其中， ${\tau }_{b,i},{\pi }_{b,i},{\alpha }_b,{\beta }_b,D{4}_b,D{5}_{b,k},D{6}_{b,k}$ 是相应的对偶变量。

约束条件(14)对偶形式为：

$\begin{array}{l}{\displaystyle \underset{i}{\sum }{\hat{F}}_{RKDE}^{(i)-1}\left(1-\alpha \right){\tau }_{1,b,i}}-{\displaystyle \underset{i}{\sum }{\hat{F}}_{RKDE}^{(i)-1}\left(\alpha \right){\pi }_{1,b,i}}+{\alpha }_{1,b}{\displaystyle \underset{i}{\sum }{r}_i^0\left(1+{\epsilon }_i\mu \right)}-{\beta }_{1,b}{\displaystyle \underset{i}{\sum }{r}_i^0\left(1-{\epsilon }_i\mu \right)}\\ +\psi D{4}_{1,b}+D{5}_{1,b,k}{r}^{cor,sum}-D{6}_{1,b,k}{r}^{cor,sum}=M_{fuel,b}^{\max }-b_{bias},\forall b\end{array}$ (30)

${\tau }_{1,b,i}-{\pi }_{1,b,i}+{\alpha }_{1,b}-{\beta }_{1,b}+{\displaystyle \underset{k}{\sum }{\sigma }_{k,i}\cdot D{5}_{1,b,k}}-{\displaystyle \underset{k}{\sum }{\sigma }_{k,i}\cdot D{6}_{1,b,k}}=M_{fuel,b},\forall i,b$ (31)

$D{4}_{1,b}+D{5}_{1,b,k}-D{6}_{1,b,k}=0，\forall b,k$ (32)

$\begin{array}{l}{\displaystyle \underset{i}{\sum }{\hat{F}}_{RKDE}^{(i)-1}\left(1-\alpha \right){\tau }_{2,b,i}}-{\displaystyle \underset{i}{\sum }{\hat{F}}_{RKDE}^{(i)-1}\left(\alpha \right){\pi }_{2,b,i}}+{\alpha }_{2,b}{\displaystyle \underset{i}{\sum }{r}_i^0\left(1+{\epsilon }_i\mu \right)}-{\beta }_{2,b}{\displaystyle \underset{i}{\sum }{r}_i^0\left(1-{\epsilon }_i\mu \right)}\\ +\psi D{4}_{2,b}+D{5}_{2,b,k}{r}^{cor,sum}-D{6}_{2,b,k}{r}^{cor,sum}=-M_{fuel,b}^{\min }+b_{bias},\forall b\end{array}$ (33)

${\tau }_{2,b,i}-{\pi }_{2,b,i}+{\alpha }_{2,b}-{\beta }_{2,b}+{\displaystyle \underset{k}{\sum }{\sigma }_{k,i}\cdot D{5}_{2,b,k}}-{\displaystyle \underset{k}{\sum }{\sigma }_{k,i}\cdot D{6}_{2,b,k}}=M_{fuel,b},\forall i,b$ (34)

$D{4}_{2,b}+D{5}_{2,b,k}-D{6}_{2,b,k}=0,\forall b,k$ (35)

${\tau }_{1,b,i},{\pi }_{1,b,i},{\alpha }_{1,b},{\beta }_{1,b},{\tau }_{2,b,i},{\pi }_{2,b,i},{\alpha }_{2,b},{\beta }_{2,b},D{4}_{1,b},D{5}_{1,b,k},D{6}_{1,b,k},D{4}_{2,b},D{5}_{2,b,k},D{6}_{2,b,k}\ge 0,\forall i,b,k$ (36)

其中， ${\tau }_{1,b,i},{\pi }_{1,b,i},{\alpha }_{1,b},{\beta }_{1,b},{\tau }_{2,b,i},{\pi }_{2,b,i},{\alpha }_{2,b},{\beta }_{2,b},D{4}_{1,b},D{5}_{1,b,k},D{6}_{1,b,k},D{4}_{2,b},D{5}_{2,b,k},D{6}_{2,b,k}$ 是相应的对偶变量。

代入原模型中替换掉对应的约束条件，即可得到原模型的鲁棒对等式：

$\underset{x}{\min }z$ (37)

约束条件，式(4)~(7)式(14)~(15)式(18)~(20)及式(22)~(36)。

综上，基于锅炉效率不确定性的鲁棒优化设计问题即解决以式(37)为目标函数，考虑约束条件式(4)~(7)式(14)~(15)式(18)~(20)及式(22)~(36)的优化问题，通过建立锅炉效率不确定集合来对不确定因素进行描述，采用鲁棒对等优化的方法把目标函数的最大最小问题转化为最小化问题，遵循约束条件求解优化。

3. 案例分析及讨论

以乙烯装置的蒸汽系统为例进行了研究，在满足系统的蒸汽需求和机械能需求的前提下，使系统的年操作费用最小，同时保证在面对不确定因素时系统的可靠性。蒸汽系统为乙烯装置提供SS，HS，MS，LS，SC五个等级的蒸汽，用于驱动压缩机或泵，总共具有14个机械能需求。

各蒸汽等级参数见表1，满足14个轴功需求，各轴功需求见表2、表3，实际工业乙烯装置中蒸汽系统的设备配置和网络结构如图3所示。

由于该蒸汽动力系统采用直接驱动式蒸汽轮机网络，系统中所有的机械能需求都直接由蒸汽轮机驱动，在优化过程中，预设汽轮机的轴功率是固定的。然而，锅炉效率由于设备效率的波动性和不确定性，会带来供应量的变化和成本变化。

从多组历史数据中得到锅炉的不确定参数，选取Hampel损失函数作为鲁棒损失函数，并采用鲁棒核密度估计的方法来构建不确定集合，设置置信水平和构建分位数函数，参考工业优化的常规预设值，把参数 $\alpha$ 设为0.05，预算参数 $\mu$ 设为0.8，平滑参数 $\sigma$ 设为0.1， $\psi$ 取3.2 [18]。通过把目标函数中的不确定性转移到约束条件的方法，将最大最小化的双层优化问题转化为单层优化问题，最后通过线性对偶理论将目标函数中的最大化问题转换为对偶形式，替换相应约束条件，求得原模型的鲁棒对等式，采用GAMS平台，CPLEX方法编程求解，完成原模型的鲁棒优化。

Table 1. Steam parameters of each grade

表1. 各等级蒸汽参数

Table 2. Mechanical energy demand 1~7

表2. 机械能需求1~7

Table 3. Mechanical energy demand 8~14

表3. 机械能需求8~14

确定性优化后具体蒸汽动力系统结构流程图见图3。

Figure 3. System structure diagram after deterministic optimization

图3. 确定性优化后的系统结构图

鲁棒优化后具体蒸汽动力系统结构流程图见图4。

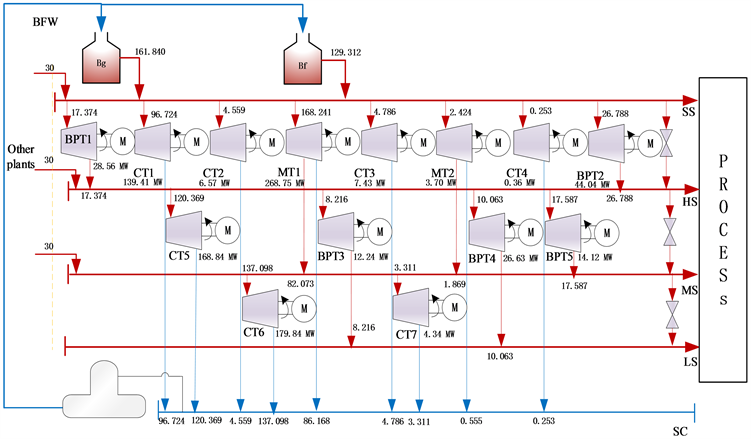
Figure 4. System structure diagram after robust optimization

图4. 鲁棒优化后的系统结构图

确定性优化和鲁棒优化后的蒸汽动力系统结构图如图3、图4表示。优化前和鲁棒优化后的设备各等级蒸汽流入、流出情况由表4、表5列出。−1表示设备在该等级处于流出状态，0表示设备在该等级处于无流通状态，为1表示设备在该等级处于流入状态。鲁棒优化在运行结构上主要减少使用SS等级做功的凝汽式汽轮机3个，增加抽气背压式汽轮机1个，在系统主要利用SS和HS两个蒸汽等级的蒸汽做功的前提下，对于各个蒸汽等级的热量的利用更加充分，并且经过系统做功后主要产物为LS, SC两个蒸汽等级的蒸汽，增加了能源利用的效率，减少热量，动能的浪费。优化前的系统的管网情况如表4所示，确定性优化和鲁棒优化与优化前相比，都增加了SS等级做功的汽轮机，对高等级的蒸汽利用更充分，从而达到优化效果。

Table 4. The pipe network situation of the system before optimization

表4. 优化前的系统的管网情况

确定性优化理想效率系统蒸汽产量、确定性优化低效率系统蒸汽产量和鲁棒优化系统蒸汽产量如表5、表6和表7所示，外购蒸汽量如图5所示，相比于鲁棒优化，确定性优化在存在LS等级的30 t/h外购蒸汽，自身的SS等级蒸汽的生产量偏低，减少单位燃料下热量更高，价格更贵的燃气锅炉产量，从理论上提高了经济效益，在经济最大化的情况下满足了蒸汽需求，但在实际生产操作中，可能受锅炉效率和最大产汽量影响存在生产缺口。

Table 5. Deterministic optimization of ideal efficiency system steam production

表5. 确定性优化理想效率系统蒸汽产量

Table 6. Deterministic optimization of steam production in low-efficiency systems

表6. 确定性优化低效率系统蒸汽产量

Table 7. Robust optimization system steam production

表7. 鲁棒优化系统蒸汽产量

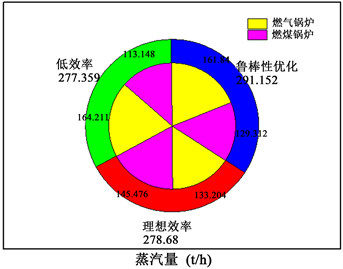
Figure 5. Optimization results of boiler steam production under different optimization conditions

图5. 不同优化条件下的锅炉产汽量优化结果

图5表示不同优化条件下的锅炉产汽量优化结果，鲁棒优化后的系统，相较与确定性优化，增加超高压蒸汽生产量约12.5 t/h，减少外购LS等级蒸汽30 t/h，两者的差别在于对高压以上的蒸汽估计用量。在实际的工业生产中，主要依靠的还是高温高压的蒸汽来满足生产所需轴功和系统外需求，对于低温低压的蒸汽在应用、运输上都比较少，鲁棒优化模型的优化结果更符合实际应用情况。

两种优化方法在不同效率下的结果如图6所示，鲁棒优化方法在理想效率下总成本增加约24.00%，在低效率下总成本降低约12.17%，在锅炉效率存在变化情况下，减小了最差结果与最优结果的波动范围，在供应量上满足可能存在的最差情况，系统在鲁棒性上提高了15.14%，使系统的经济性得到提高。

Figure 6. Changes in operating costs of two optimizations under ideal efficiency and low efficiency

图6. 两种优化在理想效率和低效率情况下的运行成本变化

4. 结论

本文通过采用数据驱动的鲁棒优化算法进行蒸汽动力系统的经济目标优化。从某化工厂得到锅炉装置效率的历史数据，然后采用鲁棒核密度估计的方法建立不确定集合，通过鲁棒对等原理对经济目标函数进行处理，建立对应的鲁棒优化模型。结果表明，鲁棒优化在理想效率下总成本增加约24.00%，在低效率下总成本降低约12.17%，鲁棒优化成本是在锅炉效率波动范围下的最优成本，所以比理想效率下的确定性优化要高出一部分，但对于系统的鲁棒性上提高了15.14%，所得的优化方案在锅炉效率全范围更优。从结果上看，考虑锅炉效率的变化，对运行成本的影响在20%左右，是运行成本中不可忽略的不确定因素，是系统成本优化的重要组成部分。鲁棒优化方法在生产上满足系统自身要求，生产较多SS等级蒸汽，可以随时通过降温降压器满足系统需求，受到外界因素影响小，并且直接考虑到锅炉效率的波动情况，所优化结果在锅炉效率波动的范围内更具有经济性。

基金项目

上海市青年科技英才扬帆项目(17YF1413100)，国家自然科学基金青年科学基金项目(62003215)。

NOTES

^*第一作者。

^#通讯作者。