非选择性半封闭捕获对具有恐惧效应的Lotka-Volterra捕食–食饵模型的动力性行为影响研究

The Influence of Non-Selective Harvesting in a Partial Closure on the Dynamic Behavior of a Lotka-Volterra Predator-Prey System with Fear Effect

摘要: 本文提出并研究一类具有非选择性半封闭捕获和恐惧效应的Lotka-Volterra捕食–食饵模型。我们的研究表明捕获会极大的影响系统的动力学行为，为了确保两个种群能有效的共存，我们需要限制捕捞区域。

Abstract: A Lotka-Volterra predator-prey system with fear effect and non-selective harvesting in a partial closure is proposed and studied in this paper. Our study shows that harvesting plays an important role on the dynamic behaviors of the system. To ensure the species coexistent in a stable state, we need to restrict the harvesting to a suitable area.

1. 前言

本文考虑如下的具有非选择性半封闭捕获和恐惧效应的Lotka-Volterra捕食–食饵模型：

$\{\begin{array}{l}\frac{\text{d}u}{\text{d}t}=u{r}_{0}f\left(k,v\right)-du-a{u}^2-puv-q_1{m}_{1}Eu,\\ \frac{\text{d}v}{\text{d}t}=cpuv-mv-q_2{m}_{1}Ev.\end{array}$ (1)

其中 $u,v$ 分别表示食饵和捕食者t在时刻的种群密度，而r₀和d分别表示食饵的出生率和死亡率，a是食饵的种内竞争，m是捕食者的死亡率，c是转化因子，k表示食饵对捕食者的恐惧程度，这里我们取

$f\left(k,v\right)=\frac{1}{1+kv}$， $q_1,q_1$ 分别为食饵和捕食者的捕捞系数； $m_1\left(0<m_1<1\right)$ 表示整块区域可供捕获的比例；

E表示为捕捞努力量。

最近，Wang等 [1] 首次将恐惧因素考虑到捕食–食饵系统中，提出具有恐惧效应的Lotka-Volterra捕食–食饵模型：

$\{\begin{array}{l}\frac{\text{d}u}{\text{d}t}=u{r}_{0}f\left(k,v\right)-du-a{u}^2-puv,\\ \frac{\text{d}v}{\text{d}t}=cpuv-mv.\end{array}$ (2)

其中 $u\left(t\right),v\left(t\right)$ 分别表示食饵和捕食者在时刻t的种群密度，而r₀和d分别表示食饵的出生率和死亡率，a是食饵的种内竞争，m是捕食者的死亡率，c是转化因子，k表示食饵对捕食者的恐惧程度。作者们对该系统的动力学行为进行了详尽的研究。

众所周知，人类会不断的开发自然资源，但如果过度的捕捞又会对生态环境造成毁灭性的破坏， 使得许多物种趋于绝灭，为了确保人类的开发和自然资源的保护能有效的协调起来，人类一般会限制捕捞区域，这样，学者们 [2] - [7] 就提出了具有半封闭捕获的各种生态学模型，并研究模型的各种动力学行为。

据笔者所知，至今尚未有学者探讨半封闭捕获对系统(2)的动力学行为影响，这启发我们提出了模型(1)。本文中，我们将对模型(1)的动力学行为进行详尽的分析。

2. 系统平衡点的存在性和局部稳定性研究

定理2.1 系统(1)总是存在一个边界平衡点 $E_0\left(0,0\right)$ ；若 $r_0>d+q_{1}E{m}_1$，系统(1)存在边界平衡点

$E_1\left(\frac{r_0-d-q_{1}E{m}_1}{a},0\right)$ ；若 $r_0>d+q_{1}E{m}_1+\frac{a\left(d+q_{2}E{m}_1\right)}{cp}$，系统(1)存在唯一的正平衡点 $E_2\left(u^{*},v^{*}\right)$，其中 $u^{*}=\frac{m+q_{2}E{m}_1}{cp}$， $v^{*}$ 满足方程 $\frac{r_0}{1+kv}-d-a^{*}-p{v}^{*}-q_{1}E{m}_1=0$。

证明：系统(1)的平衡点满足方程

$\begin{array}{l}u{r}_{0}f\left(k,v\right)-du-a{u}^2-puv-q_1{m}_{1}Eu=0,\\ cpuv-mv-q_2{m}_{1}Ev=0.\end{array}$ (3)

从(3)的第二个式子可知 $v=0$ 或者 $u=\frac{m+q_{2}E{m}_1}{cp}$。将 $v=0$ 代入(3)第一个式子得到

$r_{0}u-du-au-q_{1}E{m}_{1}u=0$ (4)

由(4)得 $u=0$ 或 $u=\frac{r_0-d-q_{1}E{m}_1}{a}$ 者。因此系统(1)总是存在一个边界平衡点 $E_0\left(0,0\right)$ ；当 $r_0>d+q_{1}E{m}_1$，系统(1)存在边界平衡点 $E_1\left(\frac{r_0-d-q_{1}E{m}_1}{a},0\right)$。

将 $u=\frac{m+q_{2}E{m}_1}{cp}$ 代入(3)第一个式子得到

$\frac{r_0}{1+kv}-d-\frac{a\left(m+q_{2}E{m}_1\right)}{cp}-pv-q_{1}E{m}_{1}u=0$ (5)

则当 $r_0>d+q_{1}E{m}_1+\frac{a\left(d+q_{2}E{m}_1\right)}{cp}$ 时，方程(2.4)存在唯一的正解 $v^{*}$，即此时系统(1)存在唯一的正平衡点

$E_2\left(u^{*},v^{*}\right)$。

定理2.1证毕。

定理2.2 若

$r_0<d+q_{1}E{m}_1$ (6)

成立，则边界平衡点 $E_0\left(0,0\right)$ 是局部渐近稳定的；

若

$d+q_{1}E{m}_1<r_0<d+q_{1}E{m}_1+\frac{a\left(d+q_{2}E{m}_1\right)}{cp}$ (7)

成立，则边界平衡点 $E_1\left(\frac{r_0-d-q_{1}E{m}_1}{a},0\right)$ 是局部渐近稳定的；

若

$r_0>d+q_{1}E{m}_1+\frac{a\left(d+q_{2}E{m}_1\right)}{cp}$ (8)

成立，则正平衡点 $E_2\left(u^{*},v^{*}\right)$ 是局部渐近稳定的。

证明：系统(1)在平衡点的Jacobian矩阵为

$J=\left(\begin{array}{cc}{J}_{11}& J_{12}\\ J_{21}& J_{22}\end{array}\right)$ (9)

其中

$\begin{array}{l}{J}_{11}=r_{0}f\left(k,v\right)-d-2au-pv-q_{1}E{m}_1,\\ J_{12}=r_{0}u\frac{\partial f\left(k,v\right)}{\partial v}-pu,\\ J_{21}=cpv,\\ J_{22}=cpu-m-q_{2}E{m}_1.\end{array}$ (10)

系统(1)在平衡点 $E_0\left(0,0\right)$ 的Jacobian矩阵为

$J\left(E_0\left(0,0\right)\right)=\left(\begin{array}{cc}{r}_0-d-q_{1}E{m}_1& 0\\ 0& -m-q_{2}E{m}_1\end{array}\right)$ (11)

矩阵 $J\left(E_0\left(0,0\right)\right)$ 的两个特征值为 ${\lambda }_1=r_0-d-q_{1}E{m}_1$， ${\lambda }_2=-m-q_{2}E{m}_1<0$，因此若 $r_0>d+q_{1}E{m}_1$ 成立，则 ${\lambda }_1<0$。即边界平衡点 $E_0\left(0,0\right)$ 是局部渐近稳定的 [8]。

记 $\bar{u}=\frac{r_0-d-q_{1}E{m}_1}{a}$，系统(1)在平衡点 $E_1\left(\bar{u},0\right)$ 的Jacobian矩阵为

$\begin{array}{c}J\left(E_1\left(\bar{u},0\right)\right)=\left(\begin{array}{cc}{r}_0-d-q_{1}E{m}_1-2a\bar{u}& r_0\bar{u}{\frac{\partial f\left(k,v\right)}{\partial v}|}_{v=0}-p\bar{u}\\ 0& cp\frac{r_0-d-q_{1}E{m}_1}{a}-m-q_{2}E{m}_1\end{array}\right)\\ =\left(\begin{array}{cc}-a\bar{u}& cp\frac{r_0-d-q_{1}E{m}_1}{a}-m-q_{2}E{m}_1\\ 0& cp\frac{r_0-d-q_{1}E{m}_1}{a}-m-q_{2}E{m}_1\end{array}\right).\end{array}$

若(7)成立，则矩阵 $J\left(E_1\left(\bar{u},0\right)\right)$ 的两个特征值为 ${\lambda }_1=-\left(r_0-d-q_{1}E{m}_1\right)$，

${\lambda }_2=cp\frac{r_0-d-q_{1}E{m}_1}{a}-m-q_{2}E{m}_1<0$，则边界平衡点 $E_1\left(\frac{r_0-d-q_{1}E{m}_1}{a},0\right)$ 是局部渐近稳定的。

系统(1)在 $E_2\left(u^{*},v^{*}\right)$ 平衡点的Jacobian矩阵为

$\begin{array}{c}J\left(E_2\left(u^{*},v^{*}\right)\right)=\left(\begin{array}{cc}{r}_{0}f\left(k,v^{*}\right)-d-2a{u}^{*}-p{v}^{*}-q_{1}E{m}_1& r_0{u}^{*}{\frac{\partial f\left(k,v\right)}{\partial v}|}_{v=v^{*}}-p{u}^{*}\\ cp{v}^{*}& cp{u}^{*}-m-q_{2}E{m}_1\end{array}\right)\\ =\left(\begin{array}{cc}-a{u}^{*}& r_0{u}^{*}{\frac{\partial f\left(k,v\right)}{\partial v}|}_{v=v^{*}}-p{u}^{*}\\ cp{v}^{*}& 0\end{array}\right).\end{array}$

则由

$\begin{array}{l}Det\left(E_2\left(u^{*},v^{*}\right)\right)=-cp{v}^{*}\left(r_0{u}^{*}{\frac{\partial f\left(k,v\right)}{\partial v}|}_{v=v^{*}}-p{u}^{*}\right)>0,\\ Tr\left(E_2\left(u^{*},v^{*}\right)\right)=-a{u}^{*}<0.\end{array}$

可知矩阵的两个特征值都小于0。即(8)成立时，正平衡点 $E_2\left(u^{*},v^{*}\right)$ 是局部渐近稳定的。

定理2.2证毕。

3. 系统平衡点的全局稳定性研究

定理3.1 若

$r_0<d+q_{1}E{m}_1$ (12)

成立，则边界平衡点 $E_0\left(0,0\right)$ 是全局渐近稳定的。

证明：作Lyapunov函数：

$V_1\left(u,v\right)=u+\frac{1}{c}v$ (13)

显然 $V_1\left(u,v\right)$ 是定义 $u>0,v>0$ 在上的连续函数，满足 $V_1\left(0,0\right)=0$， $\forall u>0,v>0$ 有 $V_1\left(u,v\right)>0$ 成立。

计算 $V_1\left(u,v\right)$ 关于t的全导数得

$\begin{array}{c}\frac{\text{d}{V}_1}{\text{d}t}=\frac{\text{d}{V}_1}{\text{d}u}\frac{\text{d}u}{\text{d}t}+\frac{\text{d}{V}_1}{\text{d}v}\frac{\text{d}v}{\text{d}t}\\ =r_{0}uf\left(k,v\right)-du-a{u}^2-puv-q_{1}E{m}_{1}u+\frac{1}{c}\left(cpuv-mv-q_{2}E{m}_{1}v\right)\\ =r_{0}uf\left(k,v\right)-du-a{u}^2-q_{1}E{m}_{1}u-\frac{m}{c}v-\frac{q_{2}E{m}_{1}v}{c}\\ <\left(r_0-d-q_{2}E{m}_1\right)u-a{u}^2-\left(\frac{m}{c}+\frac{q_{2}E{m}_{1}v}{c}\right)v.\end{array}$

从而 $\forall u>0,v>0$，都有 $\frac{\text{d}{V}_1}{\text{d}t}<0$，由此可知边界平衡点 $E_0\left(0,0\right)$ 是全局渐近稳定的。

定理3.1证毕。

定理3.2 若

$d+q_{1}E{m}_1<r_0<d+q_{1}E{m}_1+\frac{a\left(m+q_{2}E{m}_1\right)}{c\left(p+r_{0}M\right)}$ (14)

成立，则边界平衡点 $E_1\left(\frac{r_0-d-q_{1}E{m}_1}{a},0\right)$ 是全局渐近稳定的。

其中 $M={\sup }_{v\in \left[0,+\infty \right)}\left|\frac{\partial f\left(k,v\right)}{\partial v}\right|$ ；

证明：令 $\bar{u}=\frac{r_0-d-q_{1}E{m}_1}{a}$，作Lyapunov函数：

$V_1\left(u,v\right)=u-\bar{u}-\bar{u}\ln \frac{u}{\bar{u}}+\frac{1}{c}v$ (15)

显然 $V_2\left(u,v\right)$ 是定义在 $u>0,v>0$ 上的连续函数，满足有 $V_2\left(\bar{u},0\right)=0$， $\forall u\ne \bar{u},v>0$ 有 $V_2\left(u,v\right)>0$ 且

由 $f\left(k,v\right)$ 的定义可知 $\frac{\partial f\left(k,v\right)}{\partial v}<0$。

若(13)成立，则

$\begin{array}{l}\frac{m+q_{2}E{m}_1}{c}-\left(-r_0\frac{\partial f\left(k,\theta v\right)}{\partial v}+p\right)\bar{u}\\ \ge \frac{m+q_{2}E{m}_1}{c}-\left(-r_{0}M+p\right)\frac{r_0-d-q_{1}E{m}_1}{a}\end{array}$ (16)

计算关于系统(1)的正解的全导数可得

$\begin{array}{c}\frac{\text{d}{V}_1}{\text{d}t}=\frac{\text{d}{V}_1}{\text{d}u}\frac{\text{d}u}{\text{d}t}+\frac{\text{d}{V}_1}{\text{d}v}\frac{\text{d}v}{\text{d}t}\\ =\left(u-\bar{u}\right)\left(r_{0}f\left(k,v\right)-d-au-pv-q_{1}E{m}_1\right)+\frac{1}{c}\left(cpuv-mv-q_{2}E{m}_{1}v\right)\\ =\left(u-\bar{u}\right)\left(r_{0}uf\left(k,v\right)-r_0+d+q_{1}E{m}_{1}u-a\bar{u}-pv-q_{1}E{m}_1\right)+\frac{1}{c}\left(cpuv-mv-q_{2}E{m}_{1}v\right)\\ =\left(u-\bar{u}\right)\left(r_0\frac{\partial f\left(k,\theta v\right)}{\partial v}v-a\left(u-\bar{u}\right)-pv\right)+\frac{1}{c}\left(cpuv-mv-q_{2}E{m}_{1}v\right)\\ =\frac{\partial f\left(k,\theta v\right)}{\partial v}uv-a{\left(u-\bar{u}\right)}^2-\left[\frac{m+q_{2}E{m}_1}{c}-\left(r_0\frac{\partial f\left(k,\theta v\right)}{\partial v}+p\right)\bar{u}\right]v.\end{array}$

从而 $\forall u>0,v>0$，都有 $\frac{\text{d}{V}_2}{\text{d}t}<0$，因此 $\frac{\text{d}{V}_2}{\text{d}t}$ 是定负的，由此可知边界平衡点 $E_1\left(\frac{r_0-d-q_{1}E{m}_1}{a},0\right)$ 是

全局渐近稳定的。

定理3.2证毕。

定理3.3 若

$r_0>d+q_{1}E{m}_1+\frac{a\left(m+q_{2}E{m}_1\right)}{cp}$ (17)

成立，则正平衡点 $E_2\left(u^{*},v^{*}\right)$ 是全局渐近稳定的。

证明：为了证明是全局渐近稳定的，注意在条件(16)下，系统的边界平衡点都是不稳定的，而唯一的正平衡点是局部稳定的，故我们仅需证明系统(1)在第一象限内不存在极限环，因此我们考虑Dulac函数

$B\left(u,v\right)=\frac{1}{uv}$，则

$\frac{\partial \left(BP\right)}{\partial x}+\frac{\partial \left(BQ\right)}{\partial y}=-\frac{a}{v}<0$ (18)

其中

$\begin{array}{l}P\left(u,v\right)=u{r}_{0}f\left(k,v\right)-du-a{u}^2-puv-q_1{m}_{1}Eu,\\ Q\left(u,v\right)=cpuv-mv-q_2{m}_{1}Ev.\end{array}$ (19)

由Dulac判别法可知系统(1)在第一象限内不存在极限环，因此正平衡点 $E_2\left(u^{*},v^{*}\right)$ 是全局渐近稳定的。

定理3.3证毕。

4. 非选择性半封闭捕获对种群密度的影响

1) 非选择性半封闭捕获对正平衡点的影响

记

$\begin{array}{l}F\left(u^{*},v^{*},E,m_1\right)=r_{0}f\left(k,v^{*}\right)-d-a{u}^{*}-p{v}^{*}-q_1{m}_{1}E,\\ G\left(u^{*},v^{*},E,m_1\right)=cp{u}^{*}-m-q_2{m}_{1}E.\end{array}$ (20)

正平衡点 $E_2\left(u^{*},v^{*}\right)$ 满足

$\begin{array}{l}F\left(u^{*},v^{*},E,m_1\right)=0,\\ G\left(u^{*},v^{*},E,m_1\right)=0.\end{array}$ (21)

计算得 $\forall u>0,v>0,m_1\in \left(0,1\right),E\ge 0$ 都有

$J=\frac{D\left(F,G\right)}{D\left(u^{*},v^{*}\right)}=\left|\begin{array}{cc}{F}_{u^{*}}& F_{v^{*}}\\ G_{u^{*}}& G_{v^{*}}\end{array}\right|=\left|\begin{array}{cc}-a& {r_0\frac{\partial f\left(k,v\right)}{\partial v}|}_{v=v^{*}}-p\\ cp& 0\end{array}\right|=-cp\left({r_0\frac{\partial f\left(k,v\right)}{\partial v}|}_{v=v^{*}}-p\right)>0.$

则由隐函数存在定理得，在 $E_2\left(u^{*},v^{*}\right)$ 充分小领域内可从等式(19)解出两个函数

$u^{*}=u^{*}\left(E,m_1\right),v^{*}=v^{*}\left(E,m_1\right)$

计算可得

(1) $\frac{\partial u^{*}}{\partial m_1}=-\frac{1}{J}\frac{D\left(F,G\right)}{D\left(m_1,v^{*}\right)}=\frac{q_{2}E}{CP}>0$，即食饵的种群密度 $u^{*}$ 是关于 $m_1$ 的递增函数；

(2) $\frac{\partial u^{*}}{\partial E}=-\frac{1}{J}\frac{D\left(F,G\right)}{D\left(E,v^{*}\right)}=\frac{q_2{m}_1}{CP}>0$，即食饵的种群密度 $u^{*}$ 是关于E的递增函数；

(3) $\frac{\partial v^{*}}{\partial m_1}=-\frac{1}{J}\frac{D\left(F,G\right)}{D\left(u^{*},m_{!}\right)}=-\frac{1}{J}\left(a{q}_{2}E+cp{q}_{1}E\right)<0$，即捕食者的种群密度 $v^{*}$ 是关于 $m_1$ 的递减函数；

(4) $\frac{\partial v^{*}}{\partial E}=-\frac{1}{J}\frac{D\left(F,G\right)}{D\left(u^{*},E\right)}=-\frac{1}{J}\left(a{q}_2{m}_1+cp{q}_1{m}_1\right)<0$，即捕食者的种群密度 $v^{*}$ 是关于E的递减函数。

2) 半封闭捕获对系统(1)的影响

(i) 假设 $r_0<d$ 成立，则对 $\forall m_1\in \left(0,1\right)$，都有 $r_0<d+q_{1}E{m}_1$ 成立，这表明：若生态系统在没有捕获的情况下已经绝灭，则在相同条件下，具有半封闭捕获的生态系统必定绝灭。即：如果食饵的出生率过小，两个种群最终都将灭绝。

(ii) 假设 $d<r_0<d+\frac{am}{cp}$ 成立，则对没有捕获的生态系统，捕食者将趋于绝灭，食饵将保持稳定；此

时若

$m_1>\frac{r_0-d}{q_{1}E}$ (22)

成立，则捕食者和食饵都将灭绝，这表明：若可捕捞的区域太大，则捕食者和食饵都将趋于灭绝。

若

$\frac{r_0-d-\frac{am}{c\left(p+r_{0}M\right)}}{q_{1}E+\frac{a{q}_{2}E}{c\left(p+r_{0}M\right)}}<m_1<\min \left\{\frac{r_0-d}{q_{1}E},1\right\}$ (23)

成立，则捕食者将趋于灭绝而食饵种群数量保持稳定。在这种情况下，由 $\bar{u}=\frac{r_0-d-q_{1}E{m}_1}{a}$ 可知， $\bar{u}$ 是

关于E的递减函数，同时也是 $m_1$ 关于的递减函数。

这表明：若可捕捞的区域有限，则食饵的种群数量将保持稳定，食饵种群最后稳定下来的数量将随着捕捞力度和可捕捞的区域的增大而减少。

(iii) 假设 $r_0>d+\frac{am}{cp}$ 成立，则对没有捕获的生态系统，捕食者和食饵的种群数量都将趋于一个稳定

的值；

若

$m_1<\frac{r_0-d-\frac{am}{cp}}{q_{1}E+\frac{a{q}_{2}E}{cp}}$ (24)

成立，则捕食者和食饵的种群数量都将趋于稳定的值保持稳定。

这表明：当可捕捞的区域有限的情况下，捕食者和食饵将持久共存。在这种情况下，由 $\frac{\partial u^{*}}{\partial m_1}>0,\frac{\partial v^{*}}{\partial m_1}<0$

可知：食饵的种群密度 $u^{*}$ 将随着可捕捞的区域的增大而增大，而捕食者的种群密度 $v^{*}$ 却随着可捕捞的区

域的增大而减小；由 $\frac{\partial u^{*}}{\partial E}>0,\frac{\partial v^{*}}{\partial E}<0$ 可知：食饵的种群密度 $u^{*}$ 将随着捕捞力度的增大而增大，而捕食者 $v^{*}$

的种群密度却随着捕捞力度的增大而减小。产生这种情况的原因可能是人类捕捞捕食者力度的增大导致捕食者对食饵的影响减小；

同样的，当

$\frac{r_0-d-\frac{am}{c\left(p+r_{0}M\right)}}{q_{1}E+\frac{a{q}_{2}E}{c\left(p+r_{0}M\right)}}<m_1<\min \left\{\frac{r_0-d}{q_{1}E},1\right\}$ (25)

成立，其中，则捕食者将趋于灭绝而食饵种群数量仍然保持稳定。这表明：随着可捕捞的区域的增大，捕食者趋于灭绝的几率也增大了；捕捞区域进一步扩大，当 $m_1>\left(r_0-d\right)/qE$ 成立，则捕食者和食饵都灭绝。

5. 数值模拟

例5.1 考虑如下系统

$\begin{array}{l}\frac{\text{d}u}{\text{d}t}=\frac{3u}{1+kv}-u-u^2-uv-m_{1}u,\\ \frac{\text{d}v}{\text{d}t}=\frac{1}{2}uv-v-m_{1}v.\end{array}$ (26)

相对于系统(1)我们取 $r_0=1,d=2,k=a=p=q_1=m=q_2=E=1$。此时满足

$r_0=1<2=d.$

因此从定理3.1可知，系统(26)的平衡点 $E_0\left(0,0\right)$ 是全局渐近稳定的(见图1)。

从图1可以看出，当食饵的出生率比食饵的死亡率还小时，食饵将灭绝，此时食饵是捕食者的唯一食物来源，自然也就跟随食饵一起灭绝。

例5.2 考虑如下系统

$\begin{array}{l}\frac{\text{d}u}{\text{d}t}=\frac{2u}{1+kv}-u-u^2-uv-2m_{1}u,\\ \frac{\text{d}v}{\text{d}t}=\frac{1}{2}uv-v-2m_{1}v.\end{array}$ (27)

Figure 1. Global stability of the equilibrium point $E_0\left(0,0\right)$ of system (26)

图1. 系统(26)平衡点 $E_0\left(0,0\right)$ 的全局稳定性

相对应于系统(1)我们取 $r_0=2,d=1,k=a=p=q_1=q_2=1,c=0.5,E=1$。此时满足

$d=1<r_0=2<3=d+\frac{am}{cp}.$

若取 $m_1=0$，则从文献 [1] 的结果可知，生态系统在没有捕获的情况下的平衡点 $E_1\left(1,0\right)$ 是全局渐近稳定的(见图2)。

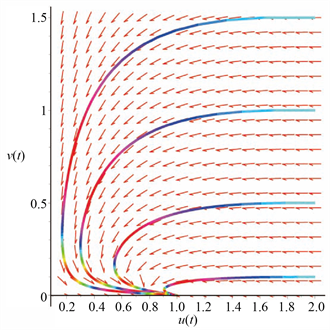
Figure 2. Global stability of the equilibrium $E_1\left(1,0\right)$ of system (27) when $m_1=0$

图2. $m_1=0$ 时，系统(27)平衡点 $E_1\left(1,0\right)$ 的全局稳定性

同时从定理3.2可知对0.1 < m₁ < 0.5，系统(27)的边界平衡点 $E_1\left(u_1\left(m_1\right),0\right)$ 是全局渐近稳定的(见图3)。

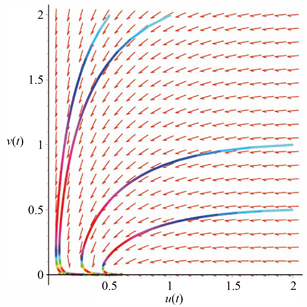
Figure 3. Global stability of the equilibrium $E_1\left(u_1\left(m_1\right),0\right)$ of system (27) when $0.1<m_1<0.5$

图3. $0.1<m_1<0.5$ 时，系统(27)边界平衡点 $E_1\left(u_1\left(m_1\right),0\right)$ 的全局稳定性

从定理3.1可知当 $0.5<m_1<1$，系统(27)的边界平衡点 $E_0\left(0,0\right)$ 是全局渐近稳定的(见图4)。

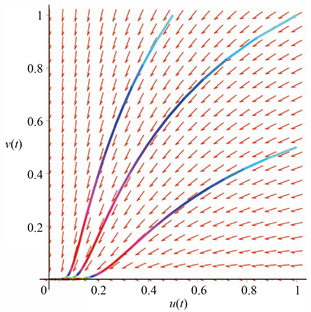
Figure 4. Global stability of the equilibrium $E_0\left(0,0\right)$ of system (27) when $0.5<m_1<1$

图4. $0.5<m_1<1$ 时，系统(27)边界平衡点 $E_0\left(0,0\right)$ 的全局稳定性

从图3和图4可知，如果不限制可捕捞区域面积，两个物种都将灭绝。

例5.3 考虑如下系统

$\begin{array}{l}\frac{\text{d}u}{\text{d}t}=\frac{3u}{1+kv}-u-u^2-uv-m_{1}u,\\ \frac{\text{d}v}{\text{d}t}=uv-v-m_{1}v.\end{array}$ (28)

相对于系统(1)我们取 $r_0=3,d=1,k=a=p=q_1=q_2=E=1$。

从定理3.3可知当 $m_1<0.5$，系统(28)的正平衡点 $E_2\left(u^{*}\left(m_1\right),v^{*}\left(m_1\right)\right)$ 是全局渐近稳定的(见图5)。计算可得系统(28)的正平衡点为

$\begin{array}{l}{u}^{*}=m_1+1,\\ v^{*}=-m_1-\frac{3}{2}+\frac{1}{2}\sqrt{4m_1^2+4m_1+3}.\end{array}$ (29)

显然 $u^{*}$ 是关于 $m_1$ 的递增函数；然而 $v^{*}$ 是关于 $m_1$ 的递减函数系统。

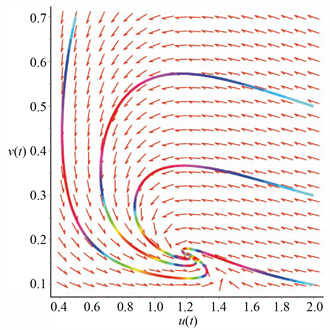
Figure 5. Global stability of the equilibrium $E_2\left(u^{*}\left(m_1\right),v^{*}\left(m_1\right)\right)$ of system (28) when $m_1<0.5$

图5. $m_1<0.5$ 时，系统(28)的正平衡点 $E_2\left(u^{*}\left(m_1\right),v^{*}\left(m_1\right)\right)$ 的全局稳定性

6. 结论

本文中，我们探讨了半封闭捕获对具有恐惧效应的Lotka-Volterra捕食–食饵模型的动力学行为影响，我们的研究表明，捕获能使得种群绝灭的概率加大，为了确保种群的可持续生存，我们要建立适当的保护区，确保物种能在保护区内不受到捕获，最终两个种群在适当条件下均可持续发展。