全概率公式的教学方法的思考

Thinking about Teaching Method of Total Probability Formula

摘要: 全概率公式是概率论与数理统计教学中的一个重点和难点内容。文中对全概率公式的授课过程进行了全新的教学设计，解释了该公式与古典概率的关系，通过例题讲述了寻找样本空间的划分的方法，最后将全概率公式应用于敏感性问题的调查中。

Abstract: The total probability formula is a key and difficult content in the teaching of probability theory and mathematical statistics. A new teaching design for the teaching process of the total probability formula is proposed, in which we explain the relationship between the formula and classical probability and tell the method of looking for the division of sample space through examples. Finally, the total probability formula is applied to the investigation of sensitive problems.

1. 引言

全概率公式是概率论中一个重要的公式，它提供了一种计算复杂情况下事件概率的有效方法，使得复杂情况下事件的概率的计算简单化。全概率公式也是概率论与数理统计教学中的难点和重点问题，然而在实际教学中，学生常常只是硬背公式，然后将问题中数据直接带入公式，对于此公式的真正含义的理解不是很透彻。针对全概率公式，在教学过程，教师需要解释什么是复杂的事件，如何把一个复杂的事件简单化，什么样的事件才是简单的事件等一系列的问题。结合作者多年实际教学经验，本文就全概率公式的教学方法给出详细的讲解过程，结合具体案例，解释该公式的具体含义，以及如何应用该公式如何求解具体的题目，最后将该公式应用于敏感性问题的调查中以调动学生的兴趣和提高解决实际问题的能力。

2. 教学过程

2.1. 概念的引入

在教学过程中，我们可以利用生活中处理复杂事件的方法来引入复杂事件简单化的方法。在生活中当我们遇到一个事情比较复杂时，我们一般需要讲这个复杂的事情分成若干部分或若干阶段来解决，然后在逐一解决各个部分，最后就可以完成整个事情。将这种思想应用复杂的事件，也就要将复杂的事件分解一些简单事件的求和，同时要求这些事件是互斥的，这样，我们就可以先求解每一个简单事件的概率，然后利用概率的性质求解复杂事件的概率。那么，如何分解这个复杂的事件呢？可以考虑先将样本空间分解为互斥的事件的和，这样自然就可以把所求的复杂事件进行相应的分解。此时可以用一个图形表示该思想(见图1)，其中B表示复杂的事件，而 $A_{\text{1}},A_{\text{2}},\cdots ,A_n$ 互斥的事件，且其和为样本空间，而每个A_i与B的乘积事件A_iB是互斥的( $i=\text{1},\text{2},\cdots ,n$ )，且有 $B=B{A}_1\cup B{A}_2\cup \cdots \cup B{A}_n$，这样就将复杂事件B表示互斥的事件A_iB的和，若 $P\left(A_{i}B\right)$ 比较容易求出，就可以求解出 $P\left(B\right)$ 的值。

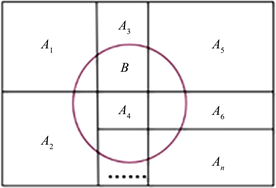
Figure 1. Decomposition of complex event B

图1. 复杂事件B的分解

2.2. 全概率公式的证明

基于以上思想，我们可以给出样本空间的划分的定义以及全概率公式的证明过程。

定义1 [1]. 样本空间的划分设S为试验E的样本空间， $A_{\text{1}},A_{\text{2}},\cdots ,A_n$ 为一组事件，若 $A_{\text{1}},A_{\text{2}},\cdots ,A_n$ 满足

1) $A_i{A}_j=\varphi ,i\ne j,i,j=1,2,\cdots ,n$ ；2) ${\displaystyle \underset{i=1}{\overset{n}{\cup }}{A}_i=S}$。

则称 $A_{\text{1}},A_{\text{2}},\cdots ,A_n$ 为样本空间S的一个划分，或称 $A_{\text{1}},A_{\text{2}},\cdots ,A_n$ 为一个完备事件组。

定理1 [1]. 设S为试验E的样本空间，A_n为S的一个划分，且 $P\left(A_i\right)>0$， $i=1,2,\cdots ,n$，则对任一事件B，有

$P\left(B\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}P\left(A_i\right)P\left(B|A_i\right)}$ (1)

公式(1)称为全概率公式。

证：由于 $A_{\text{1}},A_{\text{2}},\cdots ,A_n$ 为S的划分，所以： $A_{\text{1}},A_{\text{2}},\cdots ,A_n$ 是互斥的，且 ${\displaystyle \underset{i=1}{\overset{n}{\cup }}{A}_i=S}$

所以有

$B=B\cap S=B\cap \left(A_1\cup A_2\cup \cdots \cup A_n\right)=B{A}_1\cup B{A}_2\cup \cdots \cup B{A}_n$

且 $B{A}_{\text{1}},B{A}_{\text{2}},\cdots ,B{A}_n$ 互不相容，由概率的有限可加性得

$P\left(B\right)=P\left({\displaystyle \underset{i=1}{\overset{n}{\cup }}B{A}_i}\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}P\left(B{A}_i\right)}$

又因为 $P\left(A_i\right)>0,i=1,2,\cdots ,n$，由乘法公式

$P\left(B{A}_i\right)=P\left(A_i\right)P\left(B|A_i\right)$

所以有

$P\left(B\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}P\left(A_i\right)P\left(B|A_i\right)}$

由此可以看出，全概率公式名字的由来可以理解为：“全”部概率 $P\left(B\right)$ 被分解为许多部分之和 [2]。

2.3. 例题

以下需要用具体的例题讲解如何利用全概率公式求解具体的题目，需要重点解释该公式与古典概率的关系。由定理1知，利用全概率公式求解复杂事件B的概率，关键在于寻找样本空间的一个划分，如何寻找样本空间的划分是我们需要着重讲解的内容。

例1. 有三个箱子，分别编号为1，2，3，1号箱装有1个红球4个白球，2号箱装有2个红球3个白球，3号箱装有3个红球。某人从三个箱子中任取一个箱子，从中任意摸出一球，求摸出的是红球的概率。

分析：在讲解此例题时，首先，提出如下问题能不能按照古典概率的定义，用红球的总个数除以球的总个数进行求解呢？然后，给出本题的样本空间S的具体形式，从每个样本点的等可能性的角度解释古典概率的不可行性，接着，引出S的划分的方法，最后，利用全概率公式求解此问题。

解：记B = {从取出的箱子中任意摸出一球为红球}，A_i = {任意摸出的球取自i号箱子}，i = 1, 2, 3。

若将1号箱子中的球编号为 $\text{1},\text{2},\cdots ,\text{5}$，二号箱子中的球编号为 $\text{6},\text{7},\cdots ,\text{1}0$，3号箱子中的球编号为11, 12, 13。

则样本空间为： $S=\left\{\text{1},\text{2},\text{3},\text{4},\text{5},\text{6},\text{7},\text{8},\text{9},\text{1}0,\text{11},\text{12},\text{13}\right\}$，注意此时摸到第i号球的可能性不全相等，所以不满足古典概率的条件，故答案不能是 $\frac{6}{13}$。

易知 $A_{\text{1}}=\left\{\text{1},\text{2},\text{3},\text{4},\text{5}\right\}$， $A_{\text{2}}=\left\{\text{6},\text{7},\text{8},\text{9},\text{1}0\right\}$， $A_{\text{3}}=\left\{\text{11},\text{12},\text{13}\right\}$，即A_i，i = 1, 2, 3构成了S的一个划分。

由全概率公式可得

$P\left(B\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}P\left(A_i\right)P\left(B|A_i\right)}=\frac{1}{3}\times \frac{1}{5}+\frac{1}{3}\times \frac{2}{5}+\frac{1}{3}\times 1=\frac{8}{15}$.

由例1知，当摸出的球取自不同的箱子时，取得红球的概率的是不同的，因此，可以认为诸 $A_i\left(i=\text{1},\text{2},\text{3}\right)$ 是引起事件B的概率发生变化的原因，也就是说，所有引起事件B的概率发生变化的原因就是样本空间的划分，这为寻找样本空间的划分提供了一个简单的途径。

例2. 发报机发出“.”的概率为0.60，发出“—”的概率为0.40；收报机将“.”收为“.”的概率为0.99，将“—”收为“.”的概率为0.02。求收报机将任一信号收为“.”的概率。

解：令B ={收报机将任一信号收为“.”}，由题意知，发出的信号的不同是引起B的概率大小发生变化的原因，因此，令A₁ = {发报机发出“.”}，A₂ = {发报机发出“—”}，则A₁和A₂就组成了样本空间的一个划分。且知

$P\left(A_{\text{1}}\right)=\text{0}\text{.6},P\left(A_{\text{2}}\right)=\text{0}\text{.4},P\left(B|A_{\text{1}}\right)=\text{0}\text{.99},P\left(B|A_{\text{2}}\right)=\text{0}\text{.02}$

由全概率公式可得

$P\left(B\right)=P\left(A_{\text{1}}\right)P\left(B|A_{\text{1}}\right)+P\left(A_2\right)P\left(B|A_{\text{2}}\right)=0.6\times 0.99+0.4\times 0.02=0.602$.

2.4. 对全概率公式的理解

若将事件B看作试验的一个结果，诸A_i， $i=\text{1},\text{2},\cdots ,n$ 是引起B发生的原因(途径、条件等)，每个原因都有可能引起结果B的发生，在每个原因A_i下B发生的概率 $P\left(B|A_i\right)$ 是不同的，而试验结果B最终发生的概率就是各个原因A_i下B发生的概率 $P\left(B|A_i\right)$ 以 $P\left(A_i\right)$ 为权的加权平均值。由此可以形象的把全概率公式看成为“由原因推结果”，每个原因对结果的发生有一定的“作用”，即，结果发生的可能性与各种原因的“作用”大小有关，全概率公式表达了它们之间的关系。

2.5. 全概率公式的应用

在教学过程中，如果能利用理论知识解决实际问题，可以加深同学门对公式的理解和应用，以达到学以致用的目的。全概率公式可以应用到敏感性问题的调查中 [3] [4]。

在生活中有很多敏感性问题：“你吸大麻吗”、“你是同性恋吗”、“你是单亲家庭吗”、“你有暴力倾向吗”等等，对于这类问题，被调查者往往不愿意直接给出真实的答案，但是这类人群的比例是应该值得关注的一个重要数据。那么如何设计一个方案，即能够让被调查者如实的回答问题，且又能保守住这类人的个人隐私呢？经过多年的研究和实践，一些心理学家和统计学家设计了一种调查方案，解决了这个问题。做法如下：对被调查者提出两个问题，一个是敏感性问题S，一个是无关紧要的问题T，如S：你是同性恋吗？T：你的电话号码的最后一位数是偶数吗？一般来说，问题T的可能性的大小是已知的。然后要求被提问者投掷一枚硬币，出现正面要求正确回答S，出现反面要求正确回答T。这时提问者并不知道被提问者回答的是哪一个问题，这个信息是保密的，每个被提问者只是回答“是”或“否”，从这些结果，可以估计出同性恋人群的比例。下面利用全概率公式给出解答。

设B表示回答“是”，A₁表示掷硬币正面朝上，A₂表示掷硬币反面朝上；此时 $P\left(B|A_{\text{1}}\right)$ 就是我们关心的同性恋人群的比例， $P\left(B|A_{\text{2}}\right)$ 表示人群中电话号码最后一位为偶数的概率，是已知的。则由全概率公式

$P\left(B\right)=P\left(A_{\text{1}}\right)P\left(B|A_{\text{1}}\right)+P\left(A_{\text{2}}\right)P\left(B|A_{\text{2}}\right)=\frac{1}{2}P\left(B|A_{\text{1}}\right)+\frac{1}{2}P\left(B|A_{\text{2}}\right)$

所以有 $P\left(B|A_{\text{1}}\right)=2P\left(B\right)-P\left(B|A_{\text{2}}\right)$。

则调查结束后，可以用回答“是”的比率代替 $P\left(B\right)$，从而得到同性恋人群的比例。

3. 结论

综上所述，利用全概率公式可以求解复杂事件的概率。首先，需要确定所求的问题是否一个事件的结果；其次，需要寻找所有引起该结果的概率发生变化的原因，将其作为样本空间的划分，最后将原因和结果应用到全概率公式中进行求解。