时滞系统在对称博弈中的应用研究

Research on the Application of Time Delay System in Symmetric Game

摘要: 本文基于有限理性框架下，以2 × 2的对称博弈问题为研究对象，建立起带时滞的对称博弈模型。通过演化动力学理论中的复制动力学研究分析了博弈参与者进行策略选择的复制动态变化过程。数值模拟了带时滞与不带时滞两类系统下博弈的稳定状态。实验结果表明，在对称博弈中，决策者决策延时会对决策造成一定的影响，这个影响不改变策略的稳定状态，改变的仅是达到稳定状态的快慢程度，且时滞越长，演化到稳定状态的速度越快。

Abstract: Based on the framework of bounded rationality, this paper takes the 2 × 2 symmetric game prob-lem as the research object, establishes a symmetric game model with time delay. The dynamic change process of game participants’ strategy selection is analyzed by the study of replication dynamics in evolutionary dynamics theory. The stable state of the game under two kinds of systems with and without time delay is numerically simulated. The experimental results show that in a symmetric game, the decision-maker’s decision delay will have a certain impact on the decision. This impact does not change the steady state of the strategy, but only changes the speed of reaching the steady state. And the longer the time lag, the faster the evolution to the steady state.

1. 引言

在传统博弈论中，往往假设参与者是完全理性的，也就是说参与者是在完全信息的条件下进行的，但在现实经济生活中，参与者很难达到完全理性和完全信息的条件。演化博弈论不再把人类塑造成超理性的博弈者，而是认为人类通常通过试错来达到博弈均衡，这与生物进化的原理是一致的。因此，历史、制度因素和均衡过程的一些细节都会影响博弈中多重均衡的选择。从理论要符合实际的意义上讲，这一理论对生物学、经济学、金融学、证券学等学科都是十分有用的 [1] [2] [3]。

对于演化博弈模型，稳定解反映了未来决策的稳定性，它是通过不断调整当前决策来实现的。但是，对于有限理性的博弈参与者来说，在博弈过程中，他们往往借鉴前人的经验进行预判，而不是盲目地进行调节，即在博弈过程中会考虑先前的决策情况。本文通过时滞作用刻画了参与者决策思考的过程，建立了一个具有时滞的对称演化博弈模型，通过比较带时滞与不带时滞两类系统下决策的稳定性状态得到了一系列结论。

2. 演化博弈模型及其稳定性

2.1. 模型的假设和建立

本文以2 × 2的对称博弈问题为研究对象。假设博弈的双方都不是完全理性的，为方便起见，现假设有两个人参与了博弈，分别是参与人1和参与人2。他们分别有两种策略可以选择：策略1和策略2。如果双方都选择策略1，则双方的支付都是r；双方都选择策略2，则支付为s。当一方选择策略1，另一方选择策略2时，选择策略1的一方支付为m，选择策略2的一方支付为n。对应的支付矩阵如表1：

Table 1. Payout matrix

表1. 支付矩阵

现在考虑在一个大群体之间随机配对进行该博弈。在有限理性的前提下，假设该群体中有比例为x的参与人选择策略1，比例 $1-x$ 的参与人选择策略2，此时社会状态为 ${\left(x,1-x\right)}^{\text{T}}$，则在博弈过程中，选择策略1和策略2的参与人期望收益函数 $F_1\left(x\right)$ 、 $F_2\left(x\right)$ 及平均得益 $\bar{F}\left(x\right)$ 分别为：

$F_1\left(x\right)=xr+\left(1-x\right)m,$ (1)

$F_2\left(x\right)=xn+\left(1-x\right)s,$ (2)

$\bar{F}\left(x\right)=x{F}_1\left(x\right)+\left(1-x\right)F_2\left(x\right).$ (3)

根据Nash平衡的定义可以得到该博弈的Nash平衡如下：

1) 若 $r>n$ 成立，则 ${\left(1,0\right)}^{\text{T}}$ 为该博弈的Nash平衡；

2) 若 $s>m$ 成立，则 ${\left(0,1\right)}^{\text{T}}$ 为该博弈的Nash平衡；

3) 若存在 $0<x^{*}<1$，使 $F_1\left(x^{\ast }\right)=F_2\left(x^{\ast }\right)$，则 ${\left(x^{\ast },1-x^{\ast }\right)}^{\text{T}}$ 为该博弈的Nash平衡。

2.2. 复制动力学的演化分析

本根据复制动力学的相关定义 [4]，我们已经知道群体的策略调整动力学可表示为：

${\stackrel{\dot{}}{x}}_i=x_i\left[F_i\left(x\right)-\bar{F}\left(x\right)\right].$

此处只需在该群体中考虑选择策略1的份额x的变化情况即可，选择策略2的份额由 $1-x$ 即可得到。由此可得x的复制动力学方程：

$\stackrel{\dot{}}{x}=x\left(1-x\right)\left[x\left(r-n\right)+\left(1-x\right)\left(m-s\right)\right]=V\left(x\right).$ (4)

令 $V\left(x\right)=0$，方程(4)最多有三个均衡状态，分别为 $x_1^{\ast }=0$， $x_2^{\ast }=1$， $x_3^{\ast }=\frac{s-m}{r-m-n+s}$ ( $0\le \frac{s-m}{r-m-n+s}\le 1$ 且 $r-m-n+s\ne 0$ )。根据微分方程稳定性定理可以得到当 $V^{\prime }\left(x^{\ast }\right)<0$ 时， $x^{\ast }$ 为稳定点。

$V^{\prime }\left(x\right)=3\left(m+n-r-s\right)x^2+2\left(r+2s-2m-n\right)x+\left(m-s\right).$ (5)

根据(5)可计算得到表2所示的稳定性分析结果。

Table 2. The evolutionary steady state analysis result of the game

表2. 博弈的演化稳定状态分析结果

由表2可知，当 $x=x_1^{\ast }=0$ 稳定时，随着时间的推移，参与人都会选择策略2，当 $x=x_2^{\ast }=1$ 稳定时，随着时间的推移，参与人都会选择策略1，当 $x=x_3^{\ast }=\frac{s-m}{r-m-n+s}$ 稳定时，随着时间的推移，有 $\frac{s-m}{r-m-n+s}$ 比例的参与者趋向于选择策略1， $\frac{r-n}{r-m-n+s}$ 比例的参与者趋向于选择策略2。

3. 带时滞系统的演化博弈模型

3.1. 模型的构建

本节将引入时滞对第2节的模型进行适当改进。根据第2节的分析我们知道，在当前的社会状态下，当 $r<n$ 且 $m>s$ 时， $x_3^{\ast }=\frac{s-m}{r-m-n+s}$ 是唯一的演化稳定状态。本节将重点分析该平衡点在时滞系统中的稳定性。当一个决策者在时间t使用一个策略时，他将在随机延迟 $\tau$ 之后也就是时间为 $t+\tau$ 时刻收到他的回报。自然地，该策略的预期收益仅在该时刻确定，即 $F\left(x\left(t+\tau \right)\right)$。等价地说，一个策略在当前时间的预期收益是之前某个随机时刻的总体状态的函数 [5]。如果延迟等于 $\tau$，则在时间t时选择策略1和策略2的参与人期望收益函数 $F_1\left(x\left(t-\tau \right)\right)$ 、 $F_2\left(x\left(t-\tau \right)\right)$ 及平均得益 $\bar{F}\left(x\left(t-\tau \right)\right)$ 分别由以下公式确定：

$F_1\left(x\left(t-\tau \right)\right)=x\left(t-\tau \right)r+\left(1-x\left(t-\tau \right)\right)m,$ (6)

$F_2\left(x\left(t-\tau \right)\right)=x\left(t-\tau \right)n+\left(1-x\left(t-\tau \right)\right)s,$ (7)

$\bar{F}\left(x\left(t-\tau \right)\right)=x\left(t\right)F_1\left(x\left(t-\tau \right)\right)+\left(1-x\left(t\right)\right)F_2\left(x\left(t-\tau \right)\right).$ (8)

根据复制动力学的相关定义，相应的时滞动力学可以表示为 [6]：

$\stackrel{\dot{}}{x}=x\left(t\right)\left[F_1\left(x\left(t-\tau \right)\right)-\bar{F}\left(x\left(t-\tau \right)\right)\right]=-\left(n-r+m-s\right)x\left(t\right)\left(1-x\left(t\right)\right)\left[x\left(t-\tau \right)-x_3^{*}\right].$ (9)

令 $\delta =n-r+m-s$，则(9)可改写为：

$\stackrel{\dot{}}{x}=-\delta x\left(t\right)\left(1-x\left(t\right)\right)\left[x\left(t-\tau \right)-x_3^{*}\right],$ (10)

式(10)为时滞微分方程，下节将讨论该模型的动力学性质。

3.2. 带时滞系统的演化博弈模型稳定性分析

稳定性问题是系统分析研究的核心，本节将讨论模型(10)的稳定性。

令 $y\left(t\right)=x\left(t\right)-x_3^{*}$，则模型(10)转化为：

$\begin{array}{c}\stackrel{\dot{}}{y}\left(t\right)=-\delta x_3^{*}\left(1-x_3^{*}\right)y\left(t-\tau \right)+\delta y\left(t-\tau \right)y\left(t\right)\left[y\left(t\right)-\left(1-2x_3^{*}\right)\right]\\ =-\delta \left(y\left(t\right)+x_3^{*}\right)\left(1-y\left(t\right)-x_3^{*}\right)y\left(t-\tau \right).\end{array}$ (11)

从而，可通过研究模型(11)在 $y=0$ 的稳定性来研究模型(10)在 $x=x_3^{*}$ 的稳定性 [7]。为了讨论模型(11)在 $y=0$ 的稳定性，我们可以将式(11)在 $y=0$ 线性化，于是有：

$\stackrel{\dot{}}{y}\left(t\right)=-\delta x_3^{*}\left(1-x_3^{*}\right)y\left(t-\tau \right)=-\alpha y\left(t-\tau \right),$ (12)

其中 $\alpha =\delta x_3^{*}\left(1-x_3^{*}\right)>0$。由时滞微分方程的理论可知，式(12)的特征方程为：

$\lambda +\alpha {\text{e}}^{-\lambda \tau }=0.$ (13)

如果式(13)的所有解的实部都是负的(这意味着 $\mathrm{Re}{\lambda }_j<0,\forall j=1,2,\cdots$ )，那么式(10)对应于式(11)的均衡点 $y=0$ 的内部平衡点 $x_3^{*}$ 是稳定的。相反，如果在式(13)中存在 $\mathrm{Re}\lambda >0$ 的解，则 $x_3^{*}$ 是不稳定的 [8]。

关于方程(12)在 $y=0$ 渐进稳定的充分必要条件我们有：

$0<\tau <\frac{\pi }{2\alpha }.$ (14)

证明：根据上面的结论，我们只需证明式(14) $\iff$ 式(13)的所有根 $\lambda$ 满足 $\mathrm{Re}\lambda <0$ 即可。

充分性当 $\tau =0$ 时，方程(13)化为 $\lambda +\alpha =0$，即 $\lambda =-\alpha$ 根的分布见图1(a)。由于 $\mathrm{Re}\lambda =-\alpha <0$，所以方程(12)在 $y=0$ 是渐进稳定的。当 $\tau$ 从大于0的方向微小地增加时，同样方程(13)的所有特征根显然满足 $\mathrm{Re}\lambda <0$，即方程(12)在 $y=0$ 仍是渐进稳定的。

设当 $\tau$ 进一步增加时，方程(12)在 $y=0$ 不再渐进稳定，这时，对于使得方程(12)在 $y=0$ 不再渐进稳定的最小的 $\tau ={\tau }^{*}>0$，方程(13)的根 $\lambda$ 必将横截穿过虚轴，如图1(b)。这里需要注意到，由于 $\alpha \ne 0$，方程(13)不存在零根 $\lambda =0$。

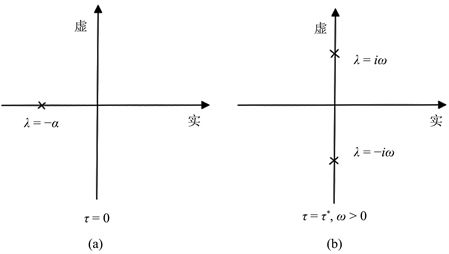
Figure 1. Distribution of roots of $\lambda +\alpha {\text{e}}^{-\lambda \tau }=0$ on the complex planet

图1. 复平面上 $\lambda +\alpha {\text{e}}^{-\lambda \tau }=0$ 的根的分布

于是当 $\tau ={\tau }^{*}$ 时，必存在 $\omega >0$ 使得下列条件至少其中一个成立：

1) $i\omega +\alpha {\text{e}}^{-i\omega {\tau }^{*}}=0$ ；

2) $-i\omega +\alpha {\text{e}}^{i\omega {\tau }^{*}}=0$。

由于这两个方程是等价的，由此可见，两个条件同时成立。

现考虑情形(1)，由于

$i\omega +\alpha {\text{e}}^{-i\omega {\tau }^{*}}=\alpha \cos \left(\omega {\tau }^{*}\right)+i\left(\omega -\alpha \sin \left(\omega {\tau }^{*}\right)\right),$ (15)

且 $\alpha >0$，则式(15)等价于

$\cos \left(\omega {\tau }^{*}\right)=0,$ (16)

且

$\sin \left(\omega {\tau }^{*}\right)=\frac{\omega }{\alpha }>0.$ (17)

由于 $\omega {\tau }^{*}>0$，于是由(16)，(17)可得：

$\omega {\tau }^{*}=\frac{\pi }{2}+2n\pi ,n=0,1,2,\cdots ,$ (18)

且

$\frac{\omega }{\alpha }=1.$ (19)

于是由(18)，(19)可得：

${\tau }^{*}=\frac{1}{\alpha }\left(\frac{\pi }{2}+2n\pi \right),n=0,1,2,\cdots .$ (20)

设 $\tau ={\tau }^{\ast }$ 时，式(13)的根在 $\lambda =i\omega$ 处首次横穿过虚轴，在式(20)中，当 $n=0$ 时，对应的 $\tau ={\tau }^{\ast }=\frac{\pi }{2\alpha }$，当 $n>0$ 时，有下列的式子成立：

$0<\tau <{\tau }^{*}=\frac{\pi }{2\alpha }.$

即若式(14)成立，式(13)的根不可能横穿过虚轴。因此，此时式(13)所有的根都满足 $\mathrm{Re}\lambda <0$，方程(12)在 $y=0$ 是渐进稳定的。

必要性事实上，我们只需证明 $\tau \ge \frac{\pi }{2\alpha }$ $\Rightarrow$ 方程(12)在 $y=0$ 不是渐进稳定的即可。

由充分性的证明和式(20)可知：

$\tau =\frac{\pi }{2\alpha }\Rightarrow \exists \omega >0$ 使得 $i\omega +\alpha {\text{e}}^{-i\omega \tau }=0$ 或者 $-i\omega +\alpha {\text{e}}^{i\omega \tau }=0$。

由式(18)可知， $\omega$ 具有形式 $\omega \tau =\frac{\pi }{2}+2n\pi \left(n=0,1,2,\cdots \right)$，且 $\lambda =\pm i\omega$ 时， $\mathrm{Re}\lambda =0$。

以下讨论当 $\tau$ 由 $\frac{\pi }{2\alpha }$ 开始微小地增加时，式(13)的根 $\lambda =\pm i\omega$ 在复平面上的变化。为此，讨论

$\mathrm{Re}{\frac{\text{d}\lambda }{\text{d}\tau }|}_{\lambda =\pm i\omega }$

的符号。方程(13)的等式两边关于 $\tau$ 求微分可得：

$\frac{\text{d}\lambda }{\text{d}\tau }-\alpha \tau {\text{e}}^{-\lambda \tau }\frac{\text{d}\lambda }{\text{d}\tau }-\alpha \lambda {\text{e}}^{-\lambda \tau }=0.$

由于 $-\alpha {\text{e}}^{-\lambda \tau }=\lambda$，因此上式可改写为：

$\frac{\text{d}\lambda }{\text{d}\tau }+\lambda \tau \frac{\text{d}\lambda }{\text{d}\tau }+{\lambda }^2=0.$

进而

$\frac{\text{d}\lambda }{\text{d}\tau }=-\frac{{\lambda }^2}{1+\lambda \tau }.$

于是

$\mathrm{Re}{\frac{\text{d}\lambda }{\text{d}\tau }|}_{\lambda =\pm i\omega }=\mathrm{Re}\frac{{\omega }^2}{1\pm i\omega \tau }=\frac{{\omega }^2}{1+{\omega }^2{\tau }^2}>0.$

这表明当 $\tau$ 由 $\frac{\pi }{2\alpha }$ 开始微小地增加时，虚轴上的根将进入右半平面，这时候方程(12)在 $y=0$ 不是渐进稳定的。

进一步，设 $\tau$ 继续增大，当增大到 $\tau =\tilde{\tau }$ 时，根 $\lambda$ 又回到虚轴上。现设对应的重虚根为 $\lambda =i\tilde{\omega }\left(\tilde{\omega }\ne 0\right)$，同上述推导类似，我们有：

$\mathrm{Re}{\frac{\text{d}\lambda }{\text{d}\tau }|}_{\lambda =i\tilde{\omega }}=\frac{{\tilde{\omega }}^2}{1+{\tilde{\omega }}^2{\tilde{\tau }}^2}>0.$

这表明当 $\tau$ 的值由 $\tilde{\tau }$ 继续微小地增加时，虚轴上的根 $\lambda =i\tilde{\omega }\left(\tilde{\omega }\ne 0\right)$ 一样地会进入右半平面，所以有：

$\tau \ge \frac{\pi }{2\alpha }\Rightarrow$ 方程(13)的根存在 $\lambda$ 满足 $\mathrm{Re}\lambda \ge 0$。

这时候方程(12)在 $y=0$ 不是渐进稳定的。证毕。

3.3. 数值仿真

为了研究分析时滞对博弈参与者决策的影响，以下将通过MATLAB进行数值模拟，取r = 3，n = 6，m = 7，s = 5，时间长度为10，初始状态为 $x\left(0\right)=0.1$。分别取时滞τ = 0.1，τ = 0.3。在MATLAB中分别调用函数ode45和dde23，得到不同情况下x的演化过程如图2所示。

(a) 正常情况 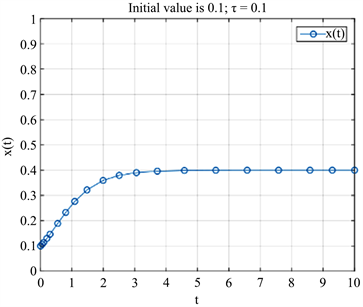(b) 时滞τ = 0.1时 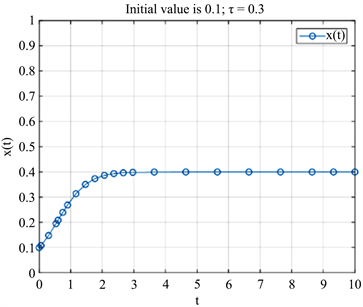(c) 时滞τ = 0.3时

Figure 2. The evolution of x in different situations

图2. 不同情况下x的演化过程

通过图2，我们可以知道，在博弈过程中，无论博弈参与者是否存在时滞行为，并不影响决策最终的稳定状态，即经过足够的时间，博弈参与者不断地进行策略调整，最后x都渐进稳定于 $x_3^{*}$，这与前面的分析完全吻合。然而，仔细观察图2的(a) (b)可知，存在时滞作用的情况下演化图像的点较为稀疏，说明时滞作用导致博弈参与者在博弈过程中学习调整策略的次数减少。这充分说明了博弈过程中参与者因考虑对方先前的决策情况从而进行决策时会慎重考虑。仔细观察图2(b)，图2(c)可知，当博弈参与者均处于时滞作用时，时滞时间越长，则x会越快演化到稳定状态。这充分说明了由于博弈参与者决策时考虑稳重，从而到达稳定策略的耗时会缩短。即谨慎行事或者计划行事在很大程度上可以避免或减少因决策失误带来的损失。

4. 结语

本文通过建立2 × 2的对称博弈模型并引入时滞仿真分析了参与人策略选择的演化过程，研究结果表明，时滞对博弈的稳定状态不会产生影响，它影响的仅仅是达到稳定状态的速率，这说明参与人在做决策时如果考虑对方先前的决策情况会大大提高决策的有效率。因此，我们可以将此结论推广到生物学、经济学、金融学和证券学等学科，只有在博弈过程中慎重决策，做到有计划地合理安排，才能在很大程度上减少因决策失误带来的损失，更快地实现各行各业均衡有效发展。