1. 前言
众所周知,岩土工程学科中有许多计算各种变量的公式,多样且复杂。因此,有必要寻求岩土学科中相关物理变量的表达式,开展相关的整理和归纳工作。在公式的整理过程中,发现平均算法在岩土工程中得到了广泛的应用,一般分为算术平均和加权平均两种。其中,算术平均是指样本个值求和除以样本个数,而加权平均数指将各数值乘以相应的频率(即权数),然后求和。
算术平均数公式和加权平均数公式如下:
1) 算术平均数公式
;
2) 加权平均数公式:若n个数为
,的权分别是
。
那么
。
若n = 2时,加权平均公式的简化形式为:
式中
,则
和
分别为a1为a2的权。
通过上述公式对比可以发现,算术平均算法容易受一组数据中极端数值(特大或特小)的影响,因此,算术平均代表性不理想;而加权平均数大小不仅取决于样本各数值大小,还取决于各数值出现的频率(即权数),不会因为极端数值(特大或特小)而影响最终结果,因此,加权平均算法更适合公式整理。为简化岩土类学科中土体容重、复合地基承载力、复合模量、平均固结度等物理变量,运用加权平均概念在岩土工程学科中对物理指标 [1] [2] 和力学指标 [3] [4] 的应用,包含(复合地基承载力 [5] [6] [7] [8] [9]、复合模量 [10]、复合地基面积置换率 [11] ),将所有形如
这个形式的岩土工程学科中的公式进行整理,并将公式采用算术平均算法进行对比,发现加权平均算法在岩土工程学科公式的使用中,可以减少数据偏差对结果的影响,使最终结果更加科学、合理。
2. 物理指标
2.1. 饱和度
土的饱和度是指土粒密度和水的密度乘以相对应的权在求和得到:
(1)
式中ρs为土粒密度,ρw为水的密度,n为孔隙率,式中n和1 − n分别为ρw和ρs的权。
2.2. 加权平均容重
加权平均容重是指在厚度为
内的土体内,不同土层容重乘以对应土层厚度进行求和,最终除以总厚度求得。而不是直接用不同土层容重之和除以土层划分总个数进行计算,更加科学、直观。
(2a)
(2b)
其中
为
的权。
3. 力学指标
在土的力学指标计算中,用到加权平均概念主要有复合模量、固结度、渗透系数、复合地基承载力等。
3.1. 复合模量
复合模量是指用桩的弹性模量和土体的模量乘以各自的权求和而得。
(3)
式中:Ep为桩弹性模量;Es为加固后桩间土压缩模量,m为面积置换率,其中m和1 − m分别为Ep和Es的权。
3.2. 固结度
土层固结度是指在假定厚度为H的土层内,如图1所示。竖向排水体范围内平均固结度和竖向排水体以下部分平均固结度乘以相对位厚度求和得出其公式:
(4)
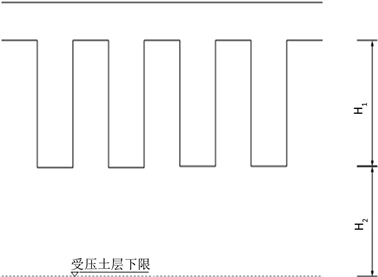
Figure 1. The vertical drainage body does not penetrate the entire compressed soil layer
图1. 竖向排水体未穿透整个受压土层
式中:H1为竖向排水体范围内土层厚度,H2为竖向排水体以下部分受压土层厚度;
Uz1为竖向排水体范围内土层的平均固结度;
Uz2为竖向排水体以下部分的土层平均固结度。
3.3. 多级加载的平均固结度计算
在实际工程中,为保证堆载预压过程中地基的稳定性,预压荷载多为分级逐渐施加。修正的方法有改进的太沙基法,修正的方法符合加权平均概念。
3.3.1. 改进的太沙基法
(5a)
当
时:
(5b)
(6)

Figure 2. Two-stage constant velocity loading process
图2. 二级等速加荷过程
其中
,如图2所示。
式中:
为多级等速加荷,t时刻修正后的平均固结度(%)。
为加荷条件下的平均固结度(%)。
加荷的起点时间和终间
为对应的第i级荷载增量。
3.4. 水平渗透的等效渗透系数
水平渗流系数是指各层渗透系数乘以相对应高度叠加之后再除以总高度可求得,如图3所示:
(7a)
(7b)
式中:kx为各土层的渗透系数,H为层状土的总厚度,Hi为各土层的厚度。
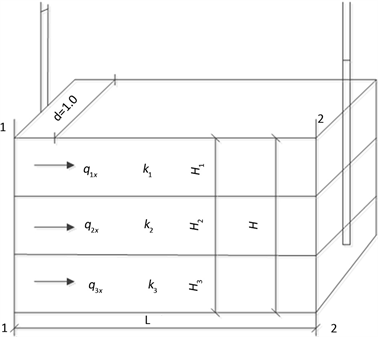
Figure 3. Schematic diagram of horizontal equivalent permeability coefficient of layered soil
图3. 层状土水平等效渗透系数示意图
3.5. 复合地基
3.5.1. 复合土体强度指标
复合地基土体抗剪强度指标可以采用面积比法计算,地基土强度τsp、复合地基土体黏聚力Csp和内摩擦角φc、地基土强度表达式如下:
(8)
(9)
(10)
式中:τsp为复合土体强度指标;τs、τp为桩间土、桩体的抗剪强度;Csp为复合地基土体黏聚力;Cs、Cp为桩间土、桩体的黏聚力;φs、φp为桩间土、桩体的内摩擦角;φc为复合地基内摩擦角;m为面积置换率。
3.5.2. 散体材料增强体复合地基承载力特征值
(11)
式中:fpk为桩身抗压强度比例界限值;fsk为桩间土承载力特征值。
3.5.3. 有黏结强度增强体复合地基承载力特征值
(12)
式中:λ为单桩承载力发挥系数,β为桩间土承载力发挥系数,可按地区经验取值。对于地基土为欠固结土、湿陷性土等特殊土时,需要选用适当的增强体和施工工艺,消除欠固结性、湿陷性、液化性等,才能形成复合地基,因此公式(12)在公式(11)的基础上添加了λ和β这两个系数,属于广义的加权平均概念公式。
3.5.4. 多型桩复合地基承载力特征值
(13)
式中:λ——单桩承载力发挥系数,可按地区经验计算;Ra——单桩竖向承载力特征值(kN);Ap——桩的截面积(m2);β——桩间土承载力发挥系数,可按地区经验取值;fsk——处理后复合地基桩间土承载力特征值(kPa)。当式中β为1的情况下,公式(13)符合加权平均概念。
4. 案例
4.1. 工程概况
拟建进贤人民医院整体搬迁项目位于南昌市进贤县北二路与贤士三路交叉口。拟建项目场地;原始地貌为丘陵地貌,现场地为荒地,现场未整平,施工条件一般。主要拟建建筑为门急诊大楼、住院楼、医技楼和食堂,通过野外钻探揭露,在钻探深度范围内,本场地表层杂填土和耕土,其下为第四系全新统沉积粉质粘土,上更新统沉积沉粉质粘土,中更新统残积层粉质粘土,下卧基岩为下第三系泥质粉砂岩和砂砾岩,按岩土层的成因类型、岩性结构、工程地质等,场地土层划分见表1。

Table 1. Comprehensive table of physical and mechanical properties of each rock and soil layer
表1. 各岩土层物理力学性质综合表
根据公式(2a)可以计算加权平均容重:
,而算术平均容重为19.34 N/m3。
当基础面积大,布桩数量多,设基础长
,基础宽
,桩径
,桩间距
,基础边缘离边庄中心距
,基础边缘离边庄中心距离为d,布桩形式如图4类似。
,单桩竖向承载力1041 kN。
将
代入公式(11)得:

Figure 4. Schematic diagram of independent foundation pile layout (d is pile diameter)
图4. 独立基础布桩示意图(d为桩径)
4.2. 数据对比
通过算术平均和加权平均算法分别计算容重和复合地基承载力,发现两种计算法计算容重差别不大,但复合地基承载力特征值算术平均值远大于加权平均值,因为fpk和fsk相差较大,再运用算术平均会导致误差较大,因此在研究岩土工程学科中变量公式会发现加权平均算法会优于算术平均算法。
5. 结论
1) 加权平均概念在土的物理性质指标及力学性质指标中有广泛的应用,通过加权平均算法,总结土的物理性质指标及力学性质指标中计算各种变量的公式,使人们更科学、直观了解加权平均容重、平均固结度、复合地基承载力等物理变量。
2) 本文通过将岩土工程学科中含有加权平均概念的公式进行归纳总结,对其他学科应用加权平均概念起到了借鉴、推广作用,有一定的参考价值。
基金项目
创新基金(YC2019072);国家基金项目(51768047)。