含区间参数非线性方程的多步区间迭代算法

Multi-Step Interval Iteration Algorithm for Nonlinear Equations with Interval Parameters

摘要: 本文在Nikas的含区间参数非线性方程的拓展区间牛顿法的基础上，结合多步区间迭代，提出了求解含区间参数非线性方程的一个拓展的多步区间迭代算法，证明新算法至少具有三阶收敛的性质，同时给出了12个数值算例，算例结果验证了新提出的多步区间迭代算法相比Nikas提出的拓展区间牛顿法在计算效率上有所提高，是有效和可靠的。

Abstract: Based on Nikas’ extended interval Newton method for nonlinear equations with interval parameters, combined with multi-step interval iteration, this paper proposes an extended multi-step interval iteration algorithm for solving nonlinear equations with interval parameters. It proves that the new algorithm has at least three order convergence, and 12 numerical examples are given at the same time. Numerical results verify that new proposed multi-step interval iteration algorithm is effective and reliable compared with the extended interval Newton method proposed by Nikas.

1. 引言

1.1. 含区间参数非线性方程

非线性问题在现实生活中有着极其广泛地应用，国内外许多学者提炼出诸多科学领域(如航天航空 [1]、气象 [2]、化学、生物 [3]、流体力学、建筑 [4] )的重要非线性方程，这些方程亟待解决。大部分情况下非线性方程很难获得精确解，通常运用数值解法求其数值解，并保证数值解与真解的误差要控制在实际问题可以接受的范围内，区间方法就是其中一种新颖的数值方法。

Moore首次将牛顿迭代法拓展成区间牛顿迭代形式，得到区间牛顿迭代法 [5]，虽然此方法适用于大部分方程，但是在导数区间扩张包含零的情况下却无法使用；1979年，Hansen对区间牛顿法进行了改进使其能在所有情况下适用，并能够收敛到方程的零解 [6]；2007年，Nikas将区间牛顿法推广到含参数的区间方程中，形成了拓展的区间牛顿法，通过逐步隔离零解区间(零解所在的区间)的端点来获得零解区间的近似，最终能准确收敛到零解区间，并用一系列例子进行数值模拟，验证了其方法的正确性 [6]。

在实际工程问题中，由于参数的测量不可能完全精确，我们经常会遇到如下形式的方程

$f\left(x;p\right)=0$ (1.1)

其中， $p\in \left[p\right],\left[p\right]\in IR$，IR为由实数表示的所有区间数全体。

为方便引入如下定义：

定义1.1设 $f:R\times IR\to IR$ 是一个连续可微的函数， ${\left[x\right]}_0$ 是初始搜索区间， $\left[p\right]$ 是包含f中所有参数的区间向量。则形如

$f\left(x;\left[p\right]\right)=0$ (1.2)

的非线性区间方程称为含参数的非线性区间方程。

(1.2)中所有零解区间包含了所有方程(1.1)中的所有零点，(1.2)的零解区间有三种情况：零区间(没有零点)、退化区间(只有一个零点或多个间断的零点)、非退化区间。显然，对于最后一种情况，零解区间包含的零点无穷多个零点，但因为(1.2)中的参数是连续变化的， $f\left(x;\left[p\right]\right)=0$ 的零点也应该是连续变化的，且零解区间的个数是有限的。因此我们不是去搜索单独的零点而是去确定所有零点所组成的区间。

根据上述解释，我们可以得到如下定义：

定义1.2 $\forall p\in \left[p\right]\in IR,f\left(x,p\right)=0$ 都有零点，所有参数遍历参数区间后形成的零点集合构成了 $f\left(x;\left[p\right]\right)=0$ 的解集，称为零解区间。

1.2. 区间分析理论的基本概念

为了后继表述的方便，我们给出如下区间分析的相关定义和规定，详细的信息可参考 [5]。

实数区间是有界闭集，且具有如下形式：

$\left[x\right]=\left[\underset{\_}{x},\bar{x}\right]=\left\{x\in R|\underset{\_}{x}\le x\le \bar{x}\right\}$

其中， $\underset{\_}{x},\bar{x}\in R$ 且 $\underset{\_}{x}\le \bar{x}$， $\underset{\_}{x}$ 表示区间下界， $\bar{x}$ 为区间上界。有界闭区间通常用IR表示。

下面介绍关于区间的四个简单概念：区间中点 $m\left(\left[x\right]\right)$ 、区间半径 $r\left(\left[x\right]\right)$ 、区间宽度 $w\left(\left[x\right]\right)$ 、区间并 $\bigsqcup$

$m\left(\left[x\right]\right)=\frac{\underset{\_}{x}+\bar{x}}{2}$

$r\left(\left[x\right]\right)=\frac{\bar{x}-\underset{\_}{x}}{2}$

$w\left(\left[x\right]\right)=\bar{x}-\underset{\_}{x}=2r\left(\left[x\right]\right)$

$\left[x\right]\bigsqcup \left[y\right]=\left[\min \left\{\underset{\_}{x},\underset{\_}{y}\right\},\max \left\{\bar{x},\bar{y}\right\}\right]$

以及区间的四则运算：

$\left[x\right]+\left[y\right]=\left[\underset{\_}{x}+\underset{\_}{y},\bar{x}+\bar{y}\right]$

$\left[x\right]-\left[y\right]=\left[\underset{\_}{x}-\bar{y},\bar{x}-\underset{\_}{y}\right]$

$\left[x\right]\cdot \left[y\right]=\left[\min \left\{\underset{\_}{x}\underset{\_}{y},\bar{x}\bar{y},\underset{\_}{x}\bar{y},\bar{x}\underset{\_}{y}\right\},\max \left\{\underset{\_}{x}\underset{\_}{y},\bar{x}\bar{y},\underset{\_}{x}\bar{y},\bar{x}\underset{\_}{y}\right\}\right]$

$\frac{\left[x\right]}{\left[y\right]}=\left[\min \left\{\frac{\bar{x}}{\bar{y}},\frac{\underset{\_}{x}}{\bar{y}},\frac{\bar{x}}{\bar{y}},\frac{\underset{\_}{x}}{\bar{y}}\right\},\max \left\{\frac{\bar{x}}{\bar{y}},\frac{\underset{\_}{x}}{\bar{y}},\frac{\bar{x}}{\bar{y}},\frac{\underset{\_}{x}}{\bar{y}}\right\}\right],0\notin \left[y\right]$

由区间并的概念可将区间四则运算转换为如下形式：

$\left[x\right]+\left[y\right]=\left\{\underset{\_}{x}+\left[y\right]\right\}\bigsqcup \left\{\bar{x}+\left[y\right]\right\}$

$\left[x\right]-\left[y\right]=\left\{\underset{\_}{x}-\left[y\right]\right\}\bigsqcup \left\{\bar{x}-\left[y\right]\right\}$

$\left[x\right]\cdot \left[y\right]=\left\{\underset{\_}{x}\cdot \left[y\right]\right\}\bigsqcup \left\{\bar{x}\cdot \left[y\right]\right\}$

$\frac{\left[x\right]}{\left[y\right]}=\left\{\frac{\underset{\_}{x}}{\left[y\right]}\right\}\bigsqcup \left\{\frac{\bar{x}}{\left[y\right]}\right\}$ (1.3)

2. 拓展的区间牛顿法(EIN)

解决参数固定的情况下的非线性区间方程 $f\left(x;p\right)=0$，通常采用普通的区间牛顿法，即

$\{\begin{array}{l}{m}_k=m\left({\left[x\right]}_k\right)\\ N\left({\left[x\right]}_k\right)=m_k-\frac{F\left(m_k\right)}{F^{\prime }\left({\left[x\right]}_k\right)}\\ {\left[x\right]}_{k+1}={\left[x\right]}_k\cap N\left({\left[x\right]}_k\right)\end{array}$ (2.1)

但对含参数的非线性区间方程(1.2)，普通的区间牛顿法应用会出现一些缺陷。例如，对于非退化的零解区间，该算法并不能收敛到(1.2)的解区间。Nikas详细论述了其在迭代过程中由于收敛到点造成的不精确问题、不能保证所求零解区间的连续性、以及其他一些病态情况 [7]。

为此Nikas提出了拓展的区间牛顿法(EIN) [7]，以下加以介绍：

对于含参数的非线性区间方程 $f\left(x,\left[p\right]\right)=0$，令 $F\left(m\left(\left[x\right]\right),\left[p\right]\right)=\left[\underset{\_}{F_m},\overline{F_m}\right]$， $F^{\prime }\left(m\left(\left[x\right]\right),\left[p\right]\right)=\left[\underset{\_}{d},\bar{d}\right]$，则(2.1)中 $N\left({\left[x\right]}_k\right)$ 可改写为

$\begin{array}{c}N\left({\left[x\right]}_k\right)=m_k-\frac{F\left(m_k,\left[p\right]\right)}{F^{\prime }\left({\left[x\right]}_k,\left[p\right]\right)}=m_k-\frac{\left[\underset{\_}{F_m},\overline{F_m}\right]}{\left[\underset{\_}{d},\bar{d}\right]}\\ =m_k-\frac{\underset{\_}{F_m}}{\left[\underset{\_}{d},\bar{d}\right]}\bigsqcup \frac{\overline{F_m}}{\left[\underset{\_}{d},\bar{d}\right]}=\left(m-\frac{\underset{\_}{F_m}}{\left[\underset{\_}{d},\bar{d}\right]}\right)\bigsqcup \left(m-\frac{\overline{F_m}}{\left[\underset{\_}{d},\bar{d}\right]}\right)\end{array}$

令 $N_L=m-\frac{\underset{\_}{F_m}}{\left[\underset{\_}{d},\bar{d}\right]}$， $N_U=m-\frac{\overline{F_m}}{\left[\underset{\_}{d},\bar{d}\right]}$，则普通区间牛顿迭代可变为拓展的区间牛顿迭代，即

$\{\begin{array}{l}{m}_k=m\left({\left[x\right]}_k\right)\\ H\left({\left[x\right]}_k\right)=N_L\bigsqcup N_U\\ {\left[x\right]}_{k+1}={\left[x\right]}_k\cap H\left({\left[x\right]}_k\right)\end{array}$ (2.2)

下面给出 [7] 中证明 $H\left({\left[x\right]}_k\right)=N_L\bigsqcup N_U$ 内部的部分零解区间 $\left[r\right]$ 的存在性的三个定理：

定理2.1 [7] 假设f是定义1.1中定义含参数的非线性连续可微区间函数，设区间方程 $f\left(x,\left[p\right]\right)=0$ 的初始区间为 $\left[x\right]$ 和零解区间为 ${\left[x\right]}^{\text{*}}\subseteq \left[x\right]$。如果 $0\in F\left(m,\left[p\right]\right)$，则内部区间

$\left[r\right]=\left[\min \left\{\overline{N_L},\overline{N_U}\right\},\max \left\{\underset{\_}{N_L},\underset{\_}{N_U}\right\}\right]$

必定存在且 $\left[r\right]\subseteq {\left[x\right]}^{\text{*}}$ (情况分为四种，见图1)。

定理2.2 [7] 假设f是定义1.1中定义含参数的非线性连续可微区间函数，设区间方程 $f\left(x,\left[p\right]\right)=0$ 的初始区间为 $\left[x\right]$ 及零解区间为 ${\left[x\right]}^{\text{*}}\subseteq \left[x\right]$。如果 $0\notin F\left(m,\left[p\right]\right)$ 且 $0\notin F^{\prime }\left(m,\left[p\right]\right)$，且内部区间 $\left[r\right]$ 存在则 $\left[r\right]\subseteq {\left[x\right]}^{\text{*}}$ (情况为两种，见图2)。

Figure 1. Four cases of theorem 2.1

图1. 定理2.1的四种情况

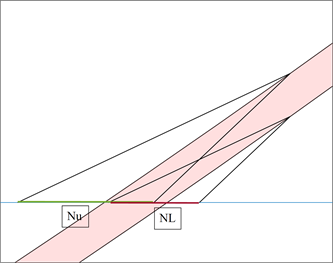
Figure 2. Two cases of theorem 2.2 ( $\left[r\right]$ in the second case does not exist)

图2. 定理2.2的两种情况(第二种中 $\left[r\right]$ 情况不存在)

定理2.3 [7] 假设f是定义1.1中定义含参数的非线性连续可微区间函数，设区间方程 $f\left(x,\left[p\right]\right)=0$ 的初始区间为 $\left[x\right]$ 及零解区间为 ${\left[x\right]}^{\text{*}}\subseteq \left[x\right]$。如果 $0\notin F\left(m,\left[p\right]\right)$ 且 $0\in F^{\prime }\left(m,\left[p\right]\right)$，此时 $\left[r\right]$ 存在，但是 $\left[r\right]\notin {\left[x\right]}^{\text{*}}$，由此可以将此区间排除(情况为两种，见图3)。

除了以上情况之外还有一种特殊情况，即当 $0\in F^{\prime }\left(m,\left[p\right]\right)$ 和 $\underset{\_}{F_m}=0$ 或 $\overline{F_m}=0$ 时，由H算子所得的新搜索区间为实数轴上的一条直线，与原搜索区间的交依然是原搜索区间，搜索区间没有减小。对于这种情况，采用启发式技术，即采用二分法对搜索区间进行人工分割，旨在避免导致这种特殊情况的产生。

3. 多步区间迭代及拓展形式

Nikas算法实质上是对含参数的非线性区间函数的上界函数 $f_U$ 与上界函数 $f_U$ 应用了点迭代的牛顿算子，容易证明，Nikas的算法收敛速度一般是有限的，只有在处理单调区间上的问题才具有二阶敛速。这启发我们将点迭代中加速牛顿算子的方法应用到Nikas算法中。下面我们介绍多步区间迭代法 [8]：

3.1. 二步区间牛顿迭代 [8]

对传统的二步牛顿迭代进行区间扩张，可以得到二步区间牛顿迭代：

Figure 3. Two cases of theorem 2.3

图3. 定理2.3的两种情况

${\left[x\right]}_{k+1}={\left[x\right]}_k\cap P\left({\left[x\right]}_k,{\left[y\right]}_k\right)$

其中，

$P\left({\left[x\right]}_k,{\left[y\right]}_k\right)=m\left({\left[y\right]}_k\right)-\frac{f\left(m\left({\left[y\right]}_k\right)\right)}{F^{\prime }\left({\left[x\right]}_k\right)}$

${\left[y\right]}_k={\left[x\right]}_k\cap N\left({\left[x\right]}_k\right)$

$N\left({\left[x\right]}_k\right)=m\left({\left[x\right]}_k\right)-\frac{f\left(m\left({\left[x\right]}_k\right)\right)}{F^{\prime }\left({\left[x\right]}_k\right)}$

3.2. 区间Ostrowski迭代 [8]

${\left[x\right]}_{k+1}={\left[x\right]}_k\cap O\left({\left[x\right]}_k,{\left[y\right]}_k\right)$

其中，

$O\left({\left[x\right]}_k,{\left[y\right]}_k\right)=m\left({\left[y\right]}_k\right)-\frac{f\left(m\left({\left[x\right]}_k\right)\right)}{\left(f\left(m\left({\left[x\right]}_k\right)\right)-2f\left(m\left({\left[y\right]}_k\right)\right)\right)F^{\prime }\left({\left[x\right]}_k\right)}f\left(m\left({\left[y\right]}_k\right)\right)$

${\left[y\right]}_k={\left[x\right]}_k\cap N\left({\left[x\right]}_k\right)$

$N\left({\left[x\right]}_k\right)=m\left({\left[x\right]}_k\right)-\frac{f\left(m\left({\left[x\right]}_k\right)\right)}{F^{\prime }\left({\left[x\right]}_k\right)}$

3.3. 区间King迭代 [8]

对King迭代法坐区间扩张也可得到如下形式：

${\left[x\right]}_{k+1}={\left[x\right]}_k\cap K\left({\left[x\right]}_k,{\left[y\right]}_k\right)$

其中，

$K\left({\left[x\right]}_k,{\left[y\right]}_k\right)=m\left({\left[y\right]}_k\right)-{\theta }_k\frac{f\left(m\left({\left[y\right]}_k\right)\right)}{F^{\prime }\left({\left[x\right]}_k\right)}$

${\left[y\right]}_k={\left[x\right]}_k\cap N\left({\left[x\right]}_k\right)$

$N\left({\left[x\right]}_k\right)=m\left({\left[x\right]}_k\right)-\frac{f\left(m\left({\left[x\right]}_k\right)\right)}{F^{\prime }\left({\left[x\right]}_k\right)}$

${\theta }_k=\frac{f\left(m\left({\left[x\right]}_k\right)\right)-\frac{1}{2}f\left(m\left({\left[y\right]}_k\right)\right)}{f\left(m\left({\left[x\right]}_k\right)\right)-\frac{5}{2}f\left(m\left({\left[y\right]}_k\right)\right)}$

由文献 [8] 可知以上区间迭代法都是至少三阶收敛的，我们将其运用到拓展的区间牛顿法的零解区间端点的逼近上，可以将拓展的区间牛顿法的收敛阶予以提高，使其以更快的速度收敛到零解区间。

4. 拓展的多步区间迭代

拓展的区间牛顿算法为：

$\{\begin{array}{l}{m}_k=m\left({\left[x\right]}_k\right)\\ H\left({\left[x\right]}_k\right)=N_L\bigsqcup N_U\\ {\left[x\right]}_{k+1}={\left[x\right]}_k\cap H\left({\left[x\right]}_k\right)\end{array}$

其中 $N_L=m-\frac{\underset{\_}{F_m}}{\left[\underset{\_}{d},\bar{d}\right]}$， $N_U=m-\frac{\overline{F_m}}{\left[\underset{\_}{d},\bar{d}\right]}$。

运用二步区间牛顿迭代修改 $N_L,N_U$ 算子为 $P_L,P_U$ 算子：

$P_L\left({\left[x\right]}_k,{\left[y\right]}_k\right)=m\left({\left[y\right]}_k\right)-\frac{\inf \left(F\left(m\left({\left[y\right]}_k\right)\right)\right)}{F^{\prime }\left({\left[x\right]}_k\right)}$

${\left[y\right]}_k={\left[x\right]}_k\cap N_L\left({\left[x\right]}_k\right)$

$N_L\left({\left[x\right]}_k\right)=m\left({\left[x\right]}_k\right)-\frac{\inf \left(F\left(m\left({\left[x\right]}_k\right)\right)\right)}{F^{\prime }\left({\left[x\right]}_k\right)}$

以及

$P_U\left({\left[x\right]}_k,{\left[y\right]}_k\right)=m\left({\left[y\right]}_k\right)-\frac{\sup \left(F\left(m\left({\left[y\right]}_k\right)\right)\right)}{F^{\prime }\left({\left[x\right]}_k\right)}$

${\left[y\right]}_k={\left[x\right]}_k\cap N_U\left({\left[x\right]}_k\right)$

$N_U\left({\left[x\right]}_k\right)=m\left({\left[x\right]}_k\right)-\frac{\sup \left(F\left(m\left({\left[x\right]}_k\right)\right)\right)}{F^{\prime }\left({\left[x\right]}_k\right)}$

由此可以得到拓展的二步区间牛顿迭代(EIN_Multi)：

$\{\begin{array}{l}{m}_k=m\left({\left[x\right]}_k\right)\\ P\left({\left[x\right]}_k\right)=P_L\bigsqcup P_U\\ {\left[x\right]}_{k+1}={\left[x\right]}_k\cap P\left({\left[x\right]}_k\right)\end{array}$

其中， $P_L=P_L\left({\left[x\right]}_k,N_L\left({\left[x\right]}_k\right)\right)$， $P_U=P_U\left({\left[x\right]}_k,N_U\left[{\left[x\right]}_k\right]\right)$。

相似的，我们也同样能得到拓展的区间Ostrowski迭代与拓展的区间King迭代：

拓展的区间Ostrowski迭代(EIN_Ostrowski)：

$\{\begin{array}{l}{m}_k=m\left({\left[x\right]}_k\right)\\ O\left({\left[x\right]}_k\right)=O_L\bigsqcup O_U\\ {\left[x\right]}_{k+1}={\left[x\right]}_k\cap O\left({\left[x\right]}_k\right)\end{array}$

其中， $O_L=O_L\left({\left[x\right]}_k,N_L\left({\left[x\right]}_k\right)\right)$， $O_U=O_U\left({\left[x\right]}_k,N_U\left({\left[x\right]}_k\right)\right)$。

拓展的区间King迭代(EIN_King)：

$\{\begin{array}{l}{m}_k=m\left({\left[x\right]}_k\right)\\ K\left({\left[x\right]}_k\right)=K_L\bigsqcup K_U\\ {\left[x\right]}_{k+1}={\left[x\right]}_k\cap K\left({\left[x\right]}_k\right)\end{array}$

其中， $K_L=K_L\left({\left[x\right]}_k,N_L\left({\left[x\right]}_k\right)\right)$， $K_U=K_U\left({\left[x\right]}_k,N_U\left({\left[x\right]}_k\right)\right)$。

引理4.1 [5] 设 $F^{\prime }\left(\left[x\right]\right)$ 为Lipschitz区间函数， $x^{\text{*}}$ 为非线性方程的实根，则存在常数 $0<c<1$，使得：

$F^{\prime }\left(\left[x\right]\right)\subseteq f^{\prime }\left(x^{\text{*}}\right)+cw\left(\left[x\right]\right)\cdot \left[-1,1\right]$

因此，存在常数 $K>0$，使得：

$w\left(\frac{1}{F^{\prime }\left(\left[x\right]\right)}\right)\le Kw\left(\left[x\right]\right)$

引理4.2 [7] 零解区间 ${\left[x\right]}^{\text{*}}\subseteq \left[x\right]$ 的端点可以被 $N_L$ 与 $N_U$ 封闭到任意精度，零解区间可以被拓展的牛顿区间迭代封闭到任意精度，且在单调区间的收敛速度至少是二阶的。

定理4.1 零解区间 ${\left[x\right]}^{\text{*}}\subseteq \left[x\right]$ 的端点可以被 $P_L$ 与 $P_U$ 封闭到任意精度，也由此可知零解区间可以被拓展的二步区间牛顿迭代封闭到任意精度，且在单调区间上拓展的二步区间牛顿收敛速度至少是三阶的。

证明：由引理4.2可知 $N_L$ 算子与 $N_U$ 算子在求解非线性函数时是收敛的，且对于单调函数零点求解时具备二阶敛速，即存在 $k_1>0$，使得：

$w\left(N_L\left({\left[x\right]}_k\right)\right)\le k_{1}w{\left({\left[x\right]}_k\right)}^2$

由中值定理可知，存在 $\xi \in N_L\left({\left[x\right]}_k\right)$，使得：

$\begin{array}{c}w\left(P_L\right)\le \left|\frac{f_L\left(m\left({\left[y\right]}_k\right)\right)}{F^{\prime }\left({\left[x\right]}_k\right)}\right|\le \left|{f^{\prime }}_L\left(\xi \right)\right|\cdot \left|m\left({\left[y\right]}_k\right)-x^{*}\right|\cdot w\left(\frac{1}{F^{\prime }\left({\left[x\right]}_k\right)}\right)\\ \le \left|{f^{\prime }}_L\left(\xi \right)\right|\cdot w\left({\left[y\right]}_k\right)\cdot w\left(\frac{1}{F^{\prime }\left({\left[x\right]}_k\right)}\right)\le \left|{f^{\prime }}_L\left(\xi \right)\right|\cdot w\left(N_L\left({\left[x\right]}_k\right)\right)\cdot w\left(\frac{1}{F^{\prime }\left({\left[x\right]}_k\right)}\right)\\ \le k_1\cdot \left|{f^{\prime }}_L\left(\xi \right)\right|\cdot w\left(\frac{1}{F^{\prime }\left({\left[x\right]}_k\right)}\right)\cdot w{\left({\left[x\right]}_k\right)}^2\end{array}$

其中 $x^{\text{*}}$ 为零解区间的一个端点。

因为 ${f^{\prime }}_L$ 在区间 $N_L\left({\left[x\right]}_k\right)$ 上连续可微，所以存在 $k_2>0$，使得 $\left|{f^{\prime }}_L\left(\xi \right)\right|\le k_2$。

由引理4.1可知，存在 $k_3>0$，使得

$w\left(\frac{1}{F^{\prime }\left({\left[x\right]}_k\right)}\right)\le k_{3}w\left({\left[x\right]}_k\right)$

即存在 $k_0>0$ 有

$w\left(P_L\right)\le k_1{k}_2{k}_{3}w{\left({\left[x\right]}_k\right)}^3\le \frac{1}{2}{k}_{0}w{\left({\left[x\right]}_k\right)}^3$

同理可以得到

$w\left(P_U\right)\le \frac{1}{2}{k}_{0}w{\left({\left[x\right]}_k\right)}^3$

所以

$w\left({\left[x\right]}_{k+1}\right)\le w\left(P_L\cup P_U\right)\le w\left(P_L\right)+w\left(P_U\right)\le k_{0}w{\left({\left[x\right]}_k\right)}^3$

上式表明拓展的二步区间牛顿在单调区间上至少具备三阶敛速，定理得证。

注：拓展的区间Ostrowski迭代和拓展的区间King迭代与拓展的区间二步牛顿迭代具有相同的收敛速度，证明方法相同，不再重复。

下面以EIN_Multi为例，给出求解含区间参数非线性方程零解区间的EIN_Multi算法，其中，S表示搜索区间(初始值为初始区间X₀)，Z为零解区间(初始值为空集)，X为迭代过程中的搜索区间，K为迭代次数，B为搜索区间采用二分的次数。

注：第1步为初始化，第2~28步为函数主体，第二步判断搜索区间是否为空集，若非空则继续搜索，第4步判断区间宽度，若小于给定精度则归入Z (零解区间)，第7~9步计算P_L与P_U，形成虚拟的零解区间r (可能为空集)，若遇到特殊情况则将搜索区间采用二分法形成两个子区间，二分次数 相应增加一个单位，之后判断r是否为空，再将其传输到Z中，相应的将非空子区间X₁与X₂传输到S中，重复迭代，每迭代一次，K增加一个单位，直至所有零解区间传输到Z中。

5. 数值算例

本节通过对比文献 [7] 的12个带区间参数的非线性方程(见表1)来检验新算法的有效性，并给出了相应的函数图像(见图4)。计算精度取为10⁻¹⁴，其中SI为初始区间，IT为迭代次数，B为二分次数，T为程序运行时间，I为区间解个数。下面我们通过数值实例来比较原始的HIN算法与新提出三种改进算法的差别。

Table 1. Test function

表1. 测试函数

Figure 4. The figures of test function

图4. 测试函数图像

由于四种方法所求零解区间一致，数值结果表明四种方法确实有效地收敛到了零解区间，差异主要存在于迭代次数，程序运行时间，二分次数三个部分，下面我们仅展示EIN_Multi所得到的具体数值结果(见表2)，其余结果汇总至对比表(表3)。表3中T1表示EIN程序所运行的时间，T2表示EIN_Multi程序所运行的时间，T3表示EIN_Ostrowski程序所运行的时间，T4表示EIN_King程序所运行的时间;IT1表示EIN方法所用的迭代次数，IT2表示EIN_Multi方法所用的迭代次数，IT3表示EIN_Ostrowski方法所用的迭代次数，IT4表示EIN_King方法所用的迭代次数，B1，B2，B3，B4所对应的方法同上。

Table 2. Numerical results are calculated by EIN_Multi

表2. EIN_Multi得出的数值结果

Table 3. Comparison table of key data of four methods

表3. 四种方法关键数据对比表

由上述对比可知在12个算例中，9个算例的收敛速度都有明显提升，对于大部分函数基于普通的二步迭代、区间Ostrowski以及区间king迭代改进的EIN相较于原有的EIN而言迭代次数以及二分步数显著减少，由于单调区间并不是贯穿整个初始区间，收敛速度在二阶与三阶之间，若求解单调函数的零解区间，则收敛速度可达三阶！第6、8、10个函数上的时间相差较小，这是由于非单调区间过多，迭代次数几乎不变，时间几乎相等。综上所述，改进的三种方法对于大多数函数都明显加快了收敛，收敛阶由二阶最高可提升至三阶速度。

6. 总结

本文提出了以多步区间迭代法为基础的HIN加速算法，在理论上证明了改进的新算法相比于HIN算法具有高一阶的收敛速度，并通过几个典型的数值算例对改进算法的性能进行了测试，数值结果表明新的算法具有较好的稳健性，这为求解各种不定参数非线性方程的工程问题提供了一种更为完善的解决办法。如何对以区间牛顿算子为基础的其他区间算法进行有效加速改进，还需要进一步的研究与探索。