1. 引言
蚊媒传染病指的是由蚊子来传播的传染病,也叫虫媒传染病。蚊媒传染病主要包括登革热、寨卡、疟疾等。近年来,蚊媒传染病在全球时有爆发,其病例数也呈现增长趋势。其中,登革热是发展速度最快的蚊媒传染病,在过去的50年间,其发病的数量迅速增长,目前全世界有将近40%的人面临着被感染的风险。登革热是登革病毒经伊蚊传播引起的一种急性传染病,主要流行于热带和亚热带国家和地区。近年来,我国曾多次出现过登革热的局部暴发,例如在2014年,我国广东省就爆发了很严重的登革热疫情。目前,能够有效减少登革热传播的唯一途径是防蚊灭蚊,比如通过大量喷洒杀虫剂减少蚊子数量。但是这种方法不仅会带来生态问题,还可能导致蚊子对杀虫剂逐渐产生抗药性。考虑到这些情况,防蚊灭蚊的措施亟待改进,应该用更长远、更环保的方法来防止蚊媒传染病的传播。
Wolbachia (沃尔巴克氏)是一类广泛分布于节肢动物和无脊椎动物生殖组织内的内共生细菌,它可以引发宿主产生多种生殖异常反应,如最常见的细胞质不兼容(CI),等等。因此,有一类新兴的控制蚊媒传染病的方法,就是使自然界中的伊蚊种群感染内共生菌Wolbachia (沃尔巴克氏)。一系列的实验证明这样可以阻断蚊子传播登革热等疾病 [1] [2] [3]。Wolbachia可以通过CI机制成功入侵自然界中的伊蚊种群,使得在伊蚊种群中,由于CI机制的作用,野外雌蚊与感染了Wolbachia的雄蚊交配所产的卵无法正常发育,但对感染Wolbachia的雌蚊无影响,并且其后代大多会感染Wolbachia,因此Wolbachia在入侵自然界的蚊群时拥有传播的优势。而且,基于Wolbachia的蚊媒控制方法是安全的。因此,利用Wolbachia阻断登革热的传播在应用上具有重要价值。早在2005年,生物学家奚志勇就在实验室里成功地使Wolbachia在埃及伊蚊中稳定传播 [3]。随着Wolbachia蚊媒控制技术的发展,建立数学模型研究Wolbachia传播动力学具有了重要意义。通过数学模型分析研究Wolbachia传播动力学,可以为感染Wolbachia的蚊子释放提供很好的策略和方案。
1990年以来,Hoffmann和Turelli建立了世代不重叠的离散模型并做了解释与分析 [4] [5]。2014年,Zheng等建立了如下时滞微分方程来研究Wolbachia传播动力学 [6]:
(1)
注意到,模型中出生函数为线性函数。一般说来,随着种群规模的增加,其成年个体的出生率和未成年个体的幸存率将下降,这是由于种群内部的竞争引起的,而蚊群的内部竞争主要发生在未成年阶段,所以单位时间内成年个体不再是线性增长。另外,基于成年个体对资源的竞争假设,模型的死亡函数为二次函数。但是大量的事实表明,成蚊之间的竞争几乎可以忽略。基于以上考虑,本文建立一个新的时滞微分方程模型,出生和幸存函数为Ricker型函数,而死亡函数用线性函数。
具体来说,我们建立以下的时滞微分方程模型
(2)
初始条件
(3)
其中
表示感染Wolbachia的蚊群规模,
表示野外蚊群规模,
,
分别为感染蚊群和野外蚊群
的出生率,
,
分别为感染蚊群和野外蚊群的死亡率,
,
分别为感染蚊群和野外蚊群以最大繁
殖率繁殖的规模,
是蚊子从交配到后代出现的平均等待时间。
关于Wolbachia入侵动力学及其它传染病模型可参见 [7] - [13] 以及其中的参考文献。例如Keeling等 [8] 建立的常微分方程模型,Huang等 [9] [10] 建立了反应扩散方程及其衍生的常微分方程模型,Hu等 [11] 建立的随机微分方程模型,Li等 [12] 建立的离散竞争模型,Huang等 [13] 建立的时滞微分方程。
本文第二节主要分析了模型(2)的动力学性质,包括解的正性、有界性,平衡点的存在性和稳定性和Hopf分支的存在性。第三节确定了Hopf分支方向和周期解的稳定性计算公式。第四节,通过数值模拟验证了理论的结论。
2. 模型(2)的平衡点的存在性、稳定性与Hopf分支出现的条件
定理1:模型(2)的满足初始条件(3)的解是非负的,并且最终有界。
证明:解的非负性显然,下面证明其有界性。令
,则
。因此有
那么
即有
同理可以得到
即有
。
下面求模型的平衡点。由
(4)
可知系统有四个平衡点
、
、
以及
。易知
,
显然,
。当
时
存在,当
时
存在。关于正平衡点存在的条件,注意到必有
,且
,即
。等价地有
。因此当
,
时,系统存在正平衡点。
下面分析各平衡点的稳定性。
定理2:对于模型(2),我们有以下结论:
(1) 当
,
时,
是全局渐近稳定的。
(2) 当
,
时,
是局部渐近稳定的。
(3) 当
时,
是局部渐近稳定的。
证明:(1) 当
,
时,只存在零平衡点
。
取
那么对
,
,有:
且
当且仅当
。因此,零解
全局渐近稳定。
(2) 将系统(2)在平衡点
进行线性化,得到如下形式:
(5)
其中
(6)
(7)
我们可以通过如下公式来求解特征方程:
(8)
在
处,其中
特征方程为
(9)
式子的前半部分,
,
,根据定理,当
时,
,即
时,满足前半部分为负实部的根。式子的后半部分,
,
,根据文献 [14] 中的定理,当
时,即
时,满足后半部分为负实部的根。
因此,
,
时,
是局部渐近稳定的。
(3) 在
处,其中
特征方程为
(10)
由于式子的后半部分必为负实部的根,因此只需要看式子的前半部分即可。其中
,
。同样根据定理,当
时,即
时,
是局部渐近稳定的。
下面,我们将确定平衡点
何时变得不稳定并发生Hopf分支。特征方程(10)可以写成
(11)
其中,
,
,
,
假设存在
,使得(11)有一对纯虚根,用
,
表示。将
带入,得到
分离实部与虚部,有
两式平方相加得到
(12)
令
,有
(13)
由于(10)至少有一个负实部的特征根,即最多有一个正实部的特征根。因此(13)最多有一个正根。当
,即
时出现纯虚根的情况,即
时。
对于
时,有
其中,
。
令
是方程(11)
时附近的特征值,那么有
和
。因此我们有下面的结论。
定理3:如果
,
,存在
,当
时,模型(2)在
处发生Hopf分支。
证明:
是方程(11)在
附近的特征值,将方程(11)对
求导,我们得到
即有
由于
和
,有
其中,
。
当
,即
时,有
。
3. Hopf分支的方向与稳定性
我们已经证明了Hopf分支的存在。接下来,我们由文献 [15] 和 [16] 中的Hopf分支定理,利用中心流形定理和规范型理论给出确定Hopf分支的方向和周期解的稳定性的计算公式。
令
,
,则有:
其中,
。
系统(2)可以写成:
(14)
其中,
,
,
,
为了简便,设
时系统在
处产生Hopf分支,
是其对应的纯虚根。令
,则
是系统的Hopf分支值。
记
,其中
,
在
上
次连续可微。
记
,对
。定义
为:
由Riesz表示定理,存在有界变差二阶函数矩阵
,
。使得:
选取
,其中
对于
,定义
则(14)可以等价的表示成:
, (15)
其中
,
,
。
对于
,其中
是2维复行向量空间,定义
进一步,对于
,
,定义双线性形式如下:
那么
与
是伴随算子,使得
。令
和
是
和
对应特征值
和
的特征向量,经过计算,我们得到下面的结果。
引理1:向量
为算子
关于特征值
的特征向量,
为算子
关于特征值
的特征向量,并且
,
,其中,
,
,
。
证明:设算子
关于特征值
的特征向量为
,故由
,
满足
通过计算得到
。同理可设算子
关于特征值
的特征向量为
,由
,得到
。
因为
要使得
,只需要取
即可。文献已证得
。
下面运用文献 [15] 中的方法,计算在
时系统在中心流形
的坐标。令
为(14)在
时的解,定义
(16)
在中心流形
上,有
,其中
和
是中心流形
在
和
方向上的局部坐标,分析在中心流形
上抽象方程(15)的解
可得
将上式重新表示为
,(17)
其中
, (18)
从(15)和(17)中,我们得到
其中
, (19)
展开上述级数并对比相应系数,我们得到
,
,
,... (20)
由(16)式有
从而有
,
,
,
,
,
与(18)对比系数得到:
接下来要计算
的值,还需要计算
和
的值。对于
,有
与(19)对比相应系数,得到
由(20)与
的定义有
由常数变易法,解得
(21)
同理有
(22)
其中
,
是二维向量,它们的值可以通过
时
的值来确定。当
时,有
因此
从(20)和
的定义可得
将(21)和(22)带入上面两个方程,可以分别得到
其中,
是三阶单位矩阵,从而可以求出
的值,下面式子的值也可以通过计算得到:
定理4:分支方向由
决定,分支周期解的稳定性由
决定,具体有:
(1) 如果
(
),则系统的Hopf分支是上临界(下临界)的。
(2) 如果
(
),则分支周期解是稳定(不稳定)的。
4. 数值模拟与总结
为了更好的展示模型的动力学稳定性,通过选取不同的参数应用MATLAB对平衡点
的稳定性进行数值模拟。当
时,分别选取不同的参数,它们的图像如图1所示。
图1所选的参数值为
,
,
,
,
,
,
。分别取初值
,
;
,
得到图中的解曲线。图1表明:当
时,
是局部渐近稳定的。
当
,
时,分别选取不同的参数,它们的图像如图2所示:
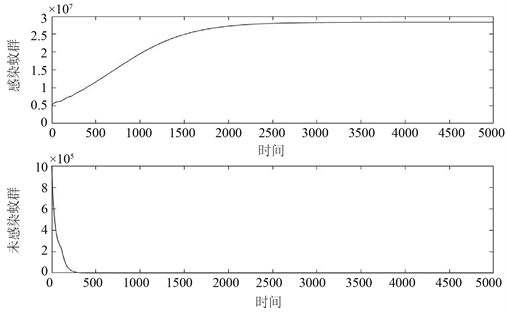
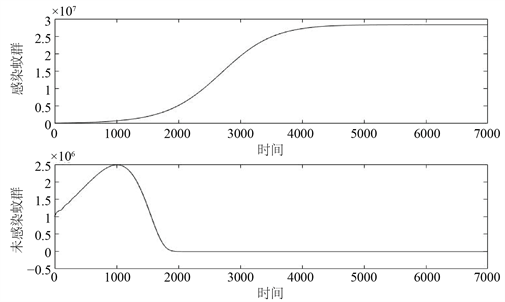
Figure 1. The solution curves of
图1.
时的解曲线
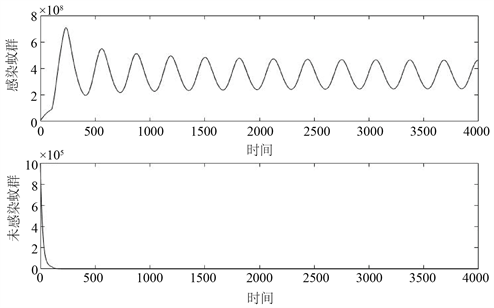
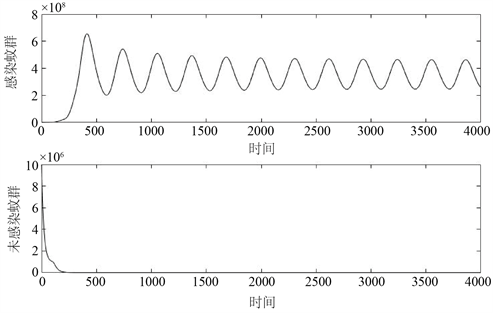
Figure 2. The solution curves of
,
图2.
,
时的解曲线
图2所选的参数值为
,
,
,
,
,
,
。
分别取初值
,
;
,
。图2表明:当
,
时,
处出现了周期解。
5. 结论
本文建立了时滞微分方程模型研究Wolbachia氏菌在蚊群中的传播,首先考虑了系统的非负性和有
界性,讨论了平衡点的存在性和在各种不同的参数条件下的稳定性态。当
时,
是局部
渐近稳定的。如果初值的选取能够使得解趋于
,则感染蚊群会持续存在,未感染蚊群会灭绝,Wolbachia
能够成功入侵到整个蚊群当中。当
,
时,
处出现了周期解,感染蚊
群和未感染蚊群的数量最终会趋于动态平衡。在这种情况下,未感染蚊群会灭绝,感染蚊群会持续存在,Wolbachia能够成功入侵到整个蚊群当中。
基金项目
国家自然科学基金(11771104)资助项目。