1. 引言
2020年3月底,新冠病毒在我国得到了基本的控制,但全球的疫情远远没有结束,社会上也出现了各种关于病毒来自哪个国家的讨论,这时候利用科学的方法来辨识病毒在微观上的差异也显得尤为重要。
DNA的一级结构决定了基因的功能,欲想解释基因的生物学含义,首先必须知道其DNA顺序。
熵,定义为信息的期望值。信息熵常作为某个系统的信息含量的量化指标,所以信息熵会进一步用来作为系统方程优化的目标或者参数选择的判据。交叉熵是Shannon信息论中一个重要概念,可以用来度量两个概率分布的相似性,而且交叉熵在神经网络中又可以用作损失函数,所以在本文中交叉熵用来衡量不同DNA之间的相似性。相对熵在信息论中等价于两个概率分布的信息熵的差值,所以在本文中可以用于衡量两个DNA的差异;三种熵则为我们提供了一种新的研究方式,在基于生物学对DNA研究的方法上,合理利用三种熵值的公式来对不同的DNA进行测量技术,最后再将结果可视化。
2. 研究结构
2.1. 信息熵
什么是信息,信息一直是一个高度抽象的概念。在1948年香农提出了“信息熵”的概念,才得以将信息度量化。而信息熵一词则是其从热力学中借用而来的,Shannon借鉴了热力学的概念,把信息中排除了冗余后的平均信息量称为“信息熵”,并给出了计算信息熵的数学表达式(见下式(1))。
(1)
2.2. 相对熵
相对熵(relative entropy),又被称为Kullback-Leibler散度(Kullback-Leibler divergence)或信息散度(information divergence),是两个概率分布(probability distribution)间差异的非对称性度量 [1]。在信息理论中,相对熵等价于两个概率分布的信息熵(Shannon entropy)的差值 [2]。
在同样的字符集上,假设存在另一个概率分布
,如果用概率分布
的最优编码,来符合分布
的字符编码那么表示这些字符就会比理想情况多用一些比特数。相对熵就是用来衡量这种情况下平均每个字符多用的比特数,因此可以用来衡量两个分布的距离(见下式(2))。
(2)
2.3. 交叉熵
交叉熵(Cross Entropy)是Shannon信息论中一个重要概念,主要用于度量两个概率分布间的差异性信息。 [3] 其公式定义如下(见下式(3)):
(3)
2.4. 新冠病毒DNA碱基序列
本次测试使用的DNA来自于国家生物信息中心(CNCB)中公开的新型冠状病毒(2019nCoVR)。
2.5. 研究方法与研究模块
2.5.1. 参数
中国地区DNA序列,共计29904个碱基;
美国地区DNA序列,共计29883个碱基;
德国地区DNA序列,共计29783个碱基;
澳大利亚地区DNA序列,共计29894个碱基。
对于每个地区分别计算序列中AG碱基的信息熵。之后计算中国对美国,中国对德国,中国对澳大利亚的交叉熵与相对熵。
2.5.2. 计量模块
如图1所示,对于每个地区,计算出序列中“AG”“CT”“AC”“AT”“GC”“GT”六种组合序列所占比,该比值则可以作为熵值计算公式中
与
来使用。
2.5.3. 处理模块
如图2所示,利用计量模块中得到频率计算熵值。得出的结果再进行下一步的可视化处理。
2.5.4. 可视化模块
如图3所示,利用Python的可视化工具,对得到的熵值进行分析。
3. 可视化结果分析
3.1. 四个地区,六种分布
如图4所示,可以看出四个地区的六种碱基序列分布基本呈现聚集的形式,符合不同地区之间新冠病毒的亲属关系,大致推断,每个地区的病毒并不是独立的;之后我们可以观察一下微观下分布的情况。

Figure 4. Six kinds of sequence frequency distribution
图4. 六种序列频率分布
如图5~10所示,六种分布可以明显的看出,不同地区的新冠病毒基因序列是有这不小的差异,虽然差异在数量级上只有0.001,但基于分析序列的所用的数据量庞大,可以知道其在宏观上是可以等价的,但是到了微观之处,该等价是不成立的。大概可以猜测六种分布的不同代表着新冠病毒在不同地区有着较为细微的差距。
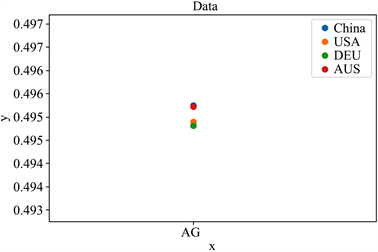
Figure 5. AG sequence frequency distribution
图5. AG序列频率分布
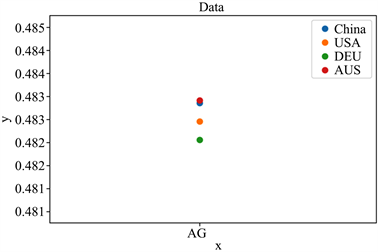
Figure 6. AC sequence frequency distribution
图6. AC序列频率分布
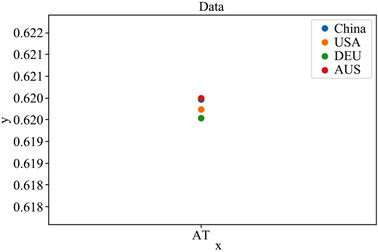
Figure 7. AT sequence frequency distribution
图7. AT序列频率分布

Figure 8. GC sequence frequency distribution
图8. GC序列频率分布
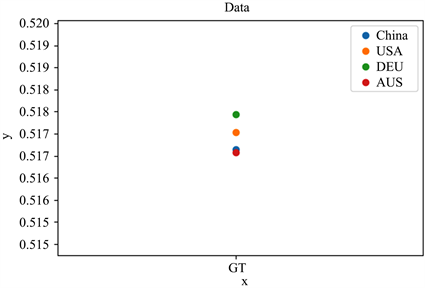
Figure 9. GT sequence frequency distribution
图 9. GT序列频率分布
3.2. 基因序列的信息熵
公式
(4)
虽然从图11中可以看出各个地区病毒序列并没有太大的差别,但每个地区之间的病毒在微观上一定是存在一定差异的,从图11中根据信息熵的定义可以看出每个地区病毒所具有的“信息量”分布是不同的。从微观的角度可以看到四个地区之间的病毒是存在差异的。
3.3. 基因中AG分布的相对熵
对于同一个随机变量AG有两个单独的概率分布P(AG)和Q(AG),相对熵来衡量这两个分布的差异。
公式
(5)
如图12所示,相对熵用于衡量AG在不同国家的新冠序列中的分布差异,可以在图12中明显的看出,中国的新冠与美国和德国的新冠的基因序列中AG分布的差别不大,但中国的新冠与澳大利亚的新冠基因序列中AG分布与中国与美国,中国与德国之间的差距却非常明显,是否可以大致推断澳大利亚的新冠与中国,美国,德国之间存在某种差异。
3.4. 基因中AG分布的交叉熵
公式
(6)
如图13所示交叉熵就是相对熵公式的前一半所得结果,此处去除的后一半是理论值,所以交叉熵更表现出真实性,而根据图13也可以看出来其结果与相对熵得出的结果一致。
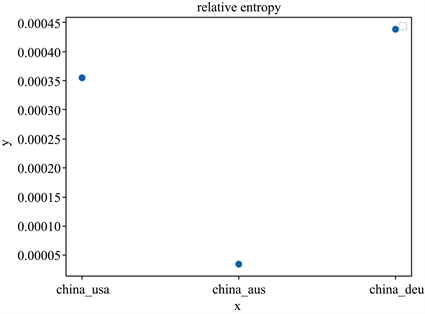
Figure 12. The relative entropy of the AG distribution
图12. AG分布的相对熵
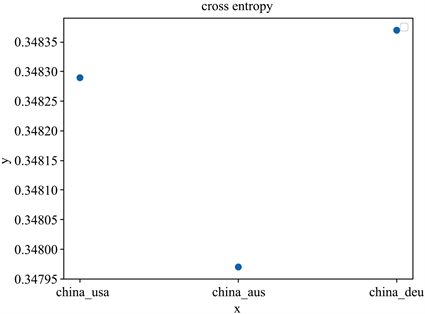
Figure 13. The cross entropy of the AG distribution
图13. AG分布的交叉熵
4. 总结
本文通过对四个地区的新型冠状病毒DNA序列信息熵,相对熵,交叉熵的计算,在实际过程中,可以主观的调节在对序列中不同碱基对的分组情况来得到结果,但最终的结果都是指向相同的结论,在此找出熵的最优值,来描述不同地区之间新冠病毒在微观上的差异,信息熵的引用与可视化的分析可以为之后关于基因的研究提供新的思路。
致谢
感谢云南大学软件学院郑智捷教授的悉心指导,以及云南大学软件学院的大力支持。
参考文献