在动静载荷作用下S型波纹管膜片非线性稳定性分析

Nonlinear Stability Analysis of S-Type Bellows Diaphragm under Dynamic and Static Loading

摘要: 研究了S型波纹管膜片的非线性稳定性问题，运用拟壳法将S型波纹管膜片当作有初挠度的圆环薄板的复合结构，利用薄壳的非线性弯曲理论，得到S型波纹管膜片在动静载荷作用下的非线性动力学方程组。在边界条件、连续条件下用Galerkin得到膜片非线性系统的受迫振动方程。用Floquet指数判断了该系统发生分叉的条件，讨论了系统在平衡点领域的稳定性问题。

Abstract: he S-shaped bellows diaphragm is regarded as the combined structure of the circular plate with initial deflection by method of simulated shell. Using the nonlinear bending theory of thin shell, the nonlinear dynamic equations of the S-shaped bellows diaphragm under static-dynamic load are obtained. According to the boundary condition and continuous condition, the forced vibration equation of diaphragm nonlinear system is obtained by Galerkin. The conditions for bifurcation of the system were determined by using Floquet index, and the stability at the equilibrium point of the system was discussed.

1. 引言

波纹管是密封系统中重要的密封元件，有着可以弥补动磨损等因素导致的轴向位移等特点，所以，波纹管干气密封也广泛应用于各种工业领域 [1]。但由于波纹管结构复杂，计算难度较大，刘静等 [2] 通过建立波纹管有限元模型，对比分析了单双层U型波纹管在液压胀形过程中的变形情况。高洪彪 [3] 通过数值模拟的方法对横向载荷作用下波纹管的变形情况进行了分析研究。阿斯耶姆·肖开提等 [4] 利用有限元分析了波纹管在机械密封中温度和应力变化。Ghader等 [5] 采用有限元法对某金属波纹管进行了数值模拟，并最终得到了最佳的设计参数。Krovvidi等 [6] 根据EJMA标准完成了高温下波纹管的初步设计，解决了波纹管的疲劳、面内、柱内失稳等破坏模式。随后，根据RCC-MR给出的准则，使用有限元分析对初步设计进行了分析验证。Hu [7] 在钱伟长研究基础上给出了，并研究了制作方法等原因引起的波纹管的厚度分布变化对波纹管刚度的影响。Chand等 [8] 通过板理论和梁理论对不同的波纹管在轴向载荷下的弯曲变形情况进行了研究分析。李树勋等 [9] 通过运用Ansys建立了U型波纹管模型，研究了波纹管在受到外压载荷和拉压位移载荷的作用下的波纹管的疲劳特性，以及在外载荷作用对波纹管疲劳寿命的影响进行了分析。宋林红等 [10] 通过疲劳模型的建立，运用Smith-Watson Topper法研究了了U型波纹管在不同工况下的疲劳寿命情况。王占彬 [11] 等通过模仿工作中的边界条件，运用数值分析的方法研究了波纹管的稳定性等问题。韩明君 [12] 等通过数值解析的方法运用拟板法及Floquet指数法，对波纹管的稳定性问题进行了研究分析。P. Dinesh Babu [13] 等通过有限元的方法对金属波纹管在其静态下的性能进行了分析研究，同时考虑了温度因素对性能的影像。Aleksander K [14] 等通过得出控制方程，采用Lagrange基本原理以及有限差分法对波纹管的应力应变的问题进行了分析研究。

以上运用多种方法对波纹管的不同问题进行了分析研究，但对S型波纹管膜片的稳定性问题的分析研究的相对比较少。文章通过研究波纹管在动静载荷下的状态，分析了S型波纹管的稳定性，并对在平衡点处的稳定性做出了分析。

2. 基本方程和边界条件

2.1. 基本方程的建立

S型波纹管膜片为圆环轴对称结构，取一半如图1所示，右边虚线为对称轴，a为波纹管膜片的外径，c为内径，b为对称中心到S型弧外侧的距离，d为对称中心到S型弧内侧的距离，h为对称中心到S型弧中间的距离，f为矢高，膜片的内外边界分别自由和固定。在膜片上施加一个均布载荷q，在内径边缘施加集中力P，如图2所示。因波纹管结构的膜片是内外焊接而成，相对变形可简化为一端固定一端自由。

Figure 1. Simplified diagram diaphragm’s model

图1. 膜片模型简化图

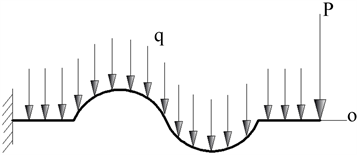
Figure 2. Mechanical model of diaphragm

图2. 膜片力学模型图

初挠度为：

$\begin{array}{l}{w}_{01}=-f\frac{{\left[r-\left(d+3R\right)\right]}^2}{R^2},\frac{\text{d}{w}_{01}}{\text{d}r}=-f\frac{2\left[r-\left(d+3R\right)\right]}{R^2}\\ w_{02}=f\frac{{\left[r-\left(d+R\right)\right]}^2}{R^2},\frac{\text{d}{w}_{02}}{\text{d}r}=f\frac{2\left[r-\left(d+R\right)\right]}{R^2}\end{array}$

S型波纹管膜片在静态载荷下的基本方程组：

$D\frac{1}{r}\frac{\text{d}}{\text{d}r}r\frac{\text{d}}{\text{d}r}\frac{1}{r}\frac{\text{d}}{\text{d}r}r\frac{\text{d}{w}_d}{\text{d}r}=q_j+\frac{1}{r}\frac{\text{d}}{\text{d}r}\left[r{N}_{rj}\left(\frac{\text{d}{w}_j}{\text{d}r}+{\lambda }_1\frac{\text{d}{w}_0}{\text{d}r}+{\lambda }_2\frac{\text{d}{w}_0}{\text{d}r}\right)\right]$ (1)

$\frac{1}{Eh}r\frac{\text{d}}{\text{d}r}\frac{1}{r}\frac{\text{d}}{\text{d}r}\left(r^2{N}_{rj}\right)=-\frac{1}{2}\left(\frac{\text{d}{w}_j}{\text{d}r}+{\lambda }_1\frac{\text{d}{w}_0}{\text{d}r}+{\lambda }_2\frac{\text{d}{w}_0}{\text{d}r}\right)\frac{\text{d}{w}_d}{\text{d}r}$ (2)

将S型波纹管的膜片在动静载荷作用下发生的非线性大挠度看作波纹管膜片具有的初挠度，并将惯性项与阻尼项计算其中，计算出在动静载荷下轴对称非线性基本方程。

$\begin{array}{l}D\frac{1}{r}\frac{\text{d}}{\text{d}r}r\frac{\text{d}}{\text{d}r}\frac{1}{r}\frac{\text{d}}{\text{d}r}r\frac{\text{d}{w}_d}{\text{d}r}\\ =q_d+\frac{1}{r}\frac{\text{d}}{\text{d}r}\left[r{N}_{rj}\frac{\text{d}{w}_d}{\text{d}r}+r{N}_{rd}\left(\frac{\text{d}{w}_j}{\text{d}r}+\frac{\text{d}{w}_d}{\text{d}r}+{\lambda }_1\frac{\text{d}{w}_0}{\text{d}r}+{\lambda }_2\frac{\text{d}{w}_0}{\text{d}r}\right)\right]-c^{\prime }\frac{d{w}_d}{dt}-\gamma \frac{{\text{d}}^2{w}_d}{\text{d}{t}^2}\end{array}$ (3)

$\frac{1}{Eh}r\frac{\text{d}}{\text{d}r}\frac{1}{r}\frac{\text{d}}{\text{d}r}\left(r^2{N}_{rd}\right)=-\frac{1}{2}\left(\frac{\text{d}{w}_d}{\text{d}r}+\frac{\text{d}{w}_j}{\text{d}r}+{\lambda }_1\frac{\text{d}{w}_0}{\text{d}r}+{\lambda }_2\frac{\text{d}{w}_0}{\text{d}r}\right)\frac{\text{d}{w}_d}{\text{d}r}$ (4)

“ ${\lambda }_1$ ”和“ ${\lambda }_2$ ”为引入的两个关于a的阶梯函数，分别为：

${\lambda }_1,{\lambda }_2$ 取值：

${\lambda }_1=\{\begin{array}{l}1,\frac{c}{a}\le x\le \frac{d}{a}\\ 0,其他\end{array}$， ${\lambda }_2=\{\begin{array}{l}-1,\frac{h}{a}\le x\le \frac{b}{a}\\ 1,\frac{d}{a}\le x\le \frac{h}{a}\\ 0,其他\end{array}$

E代表杨氏模量， $D=\frac{E{h}^3}{12\left(1-{\mu }^2\right)}$， $c^{\prime }$ 代表S型波纹管膜片的阻尼系数， $w_0$ 代表初挠度， $\gamma$ 代表S

型波纹管膜片的单位面积的体密度， $\mu$ 代表泊松比。

对方程(3) (4)进行哈密尔顿原理和变分可得，非线性动力学变分方程和协调方程。

$\begin{array}{l}{\displaystyle {\int }_{t_1}^{t_2}{\displaystyle {\int }_c^a\{D\frac{1}{r}\frac{\partial }{\partial r}r\frac{\partial }{\partial r}\frac{1}{r}\frac{\partial }{\partial r}r\frac{\partial }{\partial r}\left(w_d\right)-q_d-\frac{1}{r}\frac{\partial }{\partial r}\left[r{N}_{rj}\frac{\partial w_d}{\partial r}+r{N}_{rd}\left(\frac{\partial w_j}{\partial r}+\frac{\partial w_d}{\partial r}+{\lambda }_1\frac{\partial w_0}{\partial r}+{\lambda }_2\frac{\partial w_0}{\partial r}\right)\right]}}\\ -\frac{P}{2\pi }+c\frac{\partial w_d}{\partial t}+\gamma \frac{{\partial }^2{w}_d}{\partial t^2}\}r\delta w_d\text{d}r\text{d}t=0\end{array}$ (5)

$\frac{1}{Eh}r\frac{\partial }{\partial r}\frac{1}{r}\frac{\partial }{\partial r}\left(r^2{N}_{rd}\right)=-\left[\frac{1}{2}{\left(\frac{\partial w_d}{\partial r}\right)}^2+\frac{\partial w_j}{\partial r}\frac{\partial w_d}{\partial r}+{\lambda }_1\frac{\partial w_d}{\partial r}\frac{\partial w_0}{\partial r}+{\lambda }_2\frac{\partial w_d}{\partial r}\frac{\partial w_0}{\partial r}\right]$ (6)

边界条件为：

$r=a,w_{d(1)}=0,\frac{\text{d}{w}_{d(1)}}{\text{d}r}=0,\frac{\text{d}}{\text{d}r}\left(r{N}_{r(1)}\right)-\mu N_{r(1)}=0$ (7)

自由周边处：

$r=c,\frac{{\text{d}}^2{w}_{d(4)}}{\text{d}{r}^2}+\frac{\mu }{r}\frac{\text{d}{w}_{d(4)}}{\text{d}r}=0,N_{r(4)}=0$ (8)

连续处：

$r=b,w_{d(1)}=w_{d(2)},\frac{\text{d}{w}_{d(1)}}{\text{d}r}=\frac{\text{d}{w}_{d(2)}}{\text{d}r},M_{r(1)}=M_{r(2)},N_{r(1)}=N_{r(2)},N_{\theta (1)}=N_{\theta (2)}$ (9)

$r=h,w_{d(2)}=w_{d(3)},\frac{\text{d}{w}_{d(2)}}{\text{d}r}=\frac{\text{d}{w}_{d(3)}}{\text{d}r},M_{r(2)}=M_{r(3)},N_{r(2)}=N_{r(3)},N_{\theta (2)}=N_{\theta (3)}$ (10)

$r=d,w_{d(3)}=w_{d(4)},\frac{\text{d}{w}_{d(3)}}{\text{d}r}=\frac{\text{d}{w}_{d(4)}}{\text{d}r},M_{r(3)}=M_{r(4)},N_{r(3)}=N_{r(4)},N_{\theta (3)}=N_{\theta (4)}$ (11)

2.2. 基本方程和边界条件的无量纲化

$\begin{array}{l}x=\frac{r}{a},W=\frac{w}{h},S=\frac{12a\left(1-{\mu }^2\right)r{N}_{r}a}{E{h}^3},\beta Q=\frac{12a^4\left(1-{\mu }^2\right)q}{E{h}^4},k=f\frac{2a^2}{R^{2}h},{\varphi }_1=f\frac{2a\left(d+3R\right)}{R^{2}h},\\ {\varphi }_2=-f\frac{2a\left(d+R\right)}{R^{2}h},c^{″}=\frac{12a^4\left(1-{\mu }^2\right)}{E{h}^3}{c}^{\prime },{\gamma }_1=\frac{12a^4\left(1-{\mu }^2\right)}{E{h}^3}\gamma ,\alpha =6\left(1-{\mu }^2\right)\end{array}$

把以上量纲带入(5) (6)，计算求出无量纲变分方程(12)：

$\begin{array}{l}{\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_{\frac{c}{a}}^1\{L_1\left(W_d\right)-Q-\frac{1}{x}\frac{\partial }{\partial x}\left[S_j\frac{\partial W_d}{\partial x}+S_d\left(\frac{\partial W_j}{\partial x}+\frac{\partial W_d}{\partial x}+{\lambda }_1\left({\varphi }_1-kx\right)+{\lambda }_2\left(kx-{\varphi }_2\right)\right)\right]}}\\ +c^{″}\frac{\partial W_d}{\partial \tau }+{\gamma }_1\frac{{\partial }^2{W}_d}{\partial {\tau }^2}\}x{W}_d\text{d}x\text{d}\tau =0\end{array}$ (12)

无量纲变形协调方程：

$L_2\left(x{S}_d\right)=-\left[\alpha {\left(\frac{\partial W_d}{\partial x}\right)}^2+2\alpha \frac{\partial W_j}{\partial x}\frac{\partial W_d}{\partial x}+2\alpha \frac{\partial W_d}{\partial x}\left({\lambda }_1\left({\varphi }_1-kx\right)+{\lambda }_2\left(kx-{\varphi }_2\right)\right)\right]$ (13)

其中 $L_1=\frac{1}{x}\frac{\partial }{\partial x}x\frac{\partial }{\partial x}\frac{1}{x}\frac{\partial }{\partial x}x\frac{\partial }{\partial x}$， $L_2=x\frac{\partial }{\partial x}\frac{1}{x}\frac{\partial }{\partial x}$。

由无量纲表示的边界条件为：

固定周边处：

$x=1,W_{\text{d(1)}}=0,\frac{\text{d}{W}_{d(1)}}{\text{d}x}=0,\frac{\text{d}{S}_{d(1)}}{\text{d}x}-\mu S_{d(1)}=0$ (14)

自由周边处：

$x=\frac{c}{a},\frac{{\text{d}}^2{W}_{d(4)}}{\text{d}{x}^2}+\frac{\mu }{x}\frac{\text{d}{W}_{d(4)}}{\text{d}x}=0,S_{d(4)}=0$ (15)

连续处：

$\begin{array}{l}x=\frac{b}{a},W_{d(1)}=W_{d(2)},\frac{{\text{d}}^2{W}_{d(1)}}{\text{d}{x}^2}+\frac{\mu }{x}\frac{\text{d}{W}_{d(1)}}{\text{d}x}=\frac{{\text{d}}^2{W}_{d(2)}}{\text{d}{x}^2}+\frac{\mu }{x}\frac{\text{d}{W}_{d(2)}}{\text{d}x},\\ \frac{\text{d}{W}_{d(1)}}{\text{d}x}=\frac{\text{d}{W}_{d(2)}}{\text{d}x},S_{d(1)}=S_{d(2)},\frac{\text{d}}{\text{d}x}\left(x{S}_{d(1)}\right)=\frac{\text{d}}{\text{d}x}\left(x{S}_{d(2)}\right)\end{array}$ (16)

$\begin{array}{l}x=\frac{h}{a},W_{2(2)}=W_{d(3)},\frac{{\text{d}}^2{W}_{d(2)}}{\text{d}{x}^2}+\frac{\mu }{x}\frac{\text{d}{W}_{d(2)}}{\text{d}x}=\frac{{\text{d}}^2{W}_{d(3)}}{\text{d}{x}^2}+\frac{\mu }{x}\frac{\text{d}{W}_{d(3)}}{\text{d}x},\\ \frac{\text{d}{W}_{d(2)}}{\text{d}x}=\frac{d{W}_{d(2)}}{\text{d}x},S_{d(2)}=S_{d(3)},\frac{\text{d}}{\text{d}x}\left(x{S}_{d(2)}\right)=\frac{\text{d}}{\text{d}x}\left(x{S}_{d(3)}\right)\end{array}$ (17)

$\begin{array}{l}x=\frac{d}{a},W_{d(3)}=W_{d(4)},\frac{{\text{d}}^2{W}_{d(3)}}{\text{d}{x}^2}+\frac{\mu }{x}\frac{\text{d}{W}_{d(3)}}{\text{d}x}=\frac{{\text{d}}^2{W}_{d(4)}}{\text{d}{x}^2}+\frac{\mu }{x}\frac{\text{d}{W}_{d(4)}}{\text{d}x},\\ \frac{\text{d}{W}_{d(3)}}{\text{d}x}=\frac{\text{d}{W}_{d(4)}}{\text{d}x},S_{d(3)}=S_{d(4)},\frac{\text{d}}{\text{d}x}\left(x{S}_{d(3)}\right)=\frac{\text{d}}{\text{d}x}\left(x{S}_{d(4)}\right)\end{array}$ (18)

3. 受迫振动方程

由S型波纹管的非线性弯曲可知W_j和S_j。 $W_{j(1)},W_{j(2)},W_{j(3)},W_{j(4)}$ 比较繁长，这里不再进行展开。

$\begin{array}{c}{S}_{j(1)}=\frac{1}{x}(-\frac{1}{12288}a{Q}_1^2{x}^8-\frac{1}{384}a{Q}_1{c}_{14}{x}^6-\frac{1}{64}a{x}^4{Q}_1{c}_{15}-\frac{1}{32}a{x}^4{c}_{14}^2-\frac{1}{2}a{c}_{14}{c}_{15}\ln \left(x\right)x^2\\ +\frac{1}{4}a{c}_{14}{c}_{15}{x}^2+\frac{1}{2}a{c}_{15}^2\ln \left(x\right))+\frac{1}{2}{c}_{16}x+\frac{c_{17}}{x}\end{array}$ (19)

$\begin{array}{c}{S}_{j(2)}=\frac{1}{x}(-\frac{1}{12288}a{Q}_1^2{x}^8+\frac{1}{192}a{x}^{6}k{Q}_1-\frac{1}{384}a{Q}_1{n}_{14}{x}^6-\frac{1}{120}a{Q}_1{\varphi }_1{x}^5-\frac{1}{64}a{x}^4{Q}_1{n}_{15}\\ +\frac{1}{8}a{x}^{4}k{n}_{14}-\frac{1}{32}a{x}^4{n}_{14}^2+a{n}_{15}\ln \left(x\right)k{x}^2-\frac{1}{2}a{n}_{15}k{x}^2-\frac{1}{2}a{n}_{14}{n}_{15}\ln \left(x\right)x^2\\ +\frac{1}{4}a{n}_{14}{n}_{15}{x}^2-\frac{1}{3}a{n}_{14}{\varphi }_1{x}^3+2a{n}_{15}{\varphi }_{1}x+\frac{1}{2}a{n}_{15}^2\ln \left(x\right))+\frac{1}{2}{n}_{16}x+\frac{n_{17}}{x}\end{array}$ (20)

$\begin{array}{c}{S}_{j(3)}=\frac{1}{x}(-\frac{1}{12288}a{Q}_1^2{x}^8-\frac{1}{192}a{x}^{6}k{Q}_1-\frac{1}{384}a{Q}_1{m}_{14}{x}^6+\frac{1}{120}a{Q}_1{\varphi }_1{x}^5-\frac{1}{64}a{x}^4{Q}_1{m}_{15}\\ -\frac{1}{8}a{x}^{4}k{m}_{14}-\frac{1}{32}a{x}^4{m}_{14}^2-a{m}_{15}\ln \left(x\right)k{x}^2+\frac{1}{2}a{m}_{15}k{x}^2-\frac{1}{2}a{m}_{14}{m}_{15}\ln \left(x\right)x^2\\ +\frac{1}{4}a{m}_{14}{m}_{15}{x}^2+\frac{1}{3}a{m}_{14}{\varphi }_2{x}^3-2a{m}_{15}{\varphi }_{1}x+\frac{1}{2}a{m}_{15}^2\ln \left(x\right))+\frac{1}{2}{m}_{16}x+\frac{m_{17}}{x}\end{array}$ (21)

$\begin{array}{c}{S}_{j(4)}=\frac{1}{x}(-\frac{1}{12288}a{Q}_1^2{x}^8-\frac{1}{384}a{Q}_1{h}_{14}{x}^6-\frac{1}{64}a{x}^4{Q}_1{h}_{15}-\frac{1}{32}a{x}^4{h}_{14}^2-\frac{1}{2}a{h}_{14}{h}_{15}\ln \left(x\right)x^2\\ +\frac{1}{4}a{h}_{14}{h}_{15}{x}^2+\frac{1}{2}a{h}_{15}^2\ln \left(x\right))+\frac{1}{2}{h}_{16}x+\frac{h_{17}}{x}\end{array}$ (22)

通过边界条件可求得S型波纹管膜片在动载荷下的挠度：

$W_d=\left(\frac{1}{2}{x}^4+h_{21}{x}^2+h_{22}\ln x+h_{23}\right)f\left(t\right)$ (23)

将W_j，W_d带入方程(13)得到S_d，再将W_j，W_d，S_d，S_j带入方程(12)通过Glalerkin法并化简后可得：

$\frac{{\text{d}}^{2}f\left(t\right)}{\text{d}{t}^2}+{\phi }_0\frac{\text{d}f\left(t\right)}{\text{d}t}+{\phi }_{1}f\left(t\right)+{\phi }_2{f}^2\left(t\right)+{\phi }_3{f}^3\left(t\right)=g\cos \left(\Omega t\right)$ (24)

令 ${\phi }_1={\omega }^2$，取 $t=\omega \tau$， $f\left(t\right)=\frac{\omega }{\sqrt{{\phi }_3}}\eta \left(\tau \right)$。

由(24)可得到S型波纹管膜片线性系统的受迫振动方程：

$\frac{{\text{d}}^2\eta \left(\tau \right)}{\text{d}{\tau }^2}+{\alpha }^{\prime }\frac{\text{d}\eta \left(\tau \right)}{\text{d}\tau }+\eta \left(\tau \right)-{\chi }^{\prime }{\eta }^2\left(\tau \right)+{\eta }^3\left(\tau \right)=g^{\prime }\cos \left(\frac{\Omega }{\omega }\tau \right)$ (25)

其中 ${\alpha }^{\prime }=\frac{{\phi }_0}{\omega },{\chi }^{\prime }=-\frac{{\phi }_2}{\omega \sqrt{{\phi }_3}},g^{\prime }=\frac{g\sqrt{{\phi }_3}}{{\omega }^2}$。

4. 对自由振动方程求解

方程(25)的等价方程为：

$\{\begin{array}{l}{{\eta }^{\prime }}_1\left(\tau \right)={\eta }_2\left(\tau \right)\\ {{\eta }^{\prime }}_2\left(\tau \right)=-{\alpha }^{\prime }{\eta }_1\left(\tau \right)-{\eta }^3\left(\tau \right)+{\chi }^{\prime }{\eta }_1^2\left(\tau \right)-{\eta }_1^3\left(\tau \right)+g^{\prime }\cos \left(\frac{\Omega }{\omega }\tau \right)\end{array}$ (26)

令方程(26) ${\alpha }^{\prime }=0$ 和 $g^{\prime }=0$，则方程为：

$\{\begin{array}{l}{{\eta }^{\prime }}_1\left(\tau \right)={\eta }_2\left(\tau \right)\\ {{\eta }^{\prime }}_2\left(\tau \right)=-{\eta }^3\left(\tau \right)+{\chi }^{\prime }{\eta }_1^2\left(\tau \right)-{\eta }_1^3\left(\tau \right)\end{array}$ (27)

得该系统的Hamilton初积分为：

$H\left({\eta }_1\left(\tau \right),{\eta }_2\left(\tau \right)\right)=\frac{{\left({{\eta }^{\prime }}_1\left(\tau \right)\right)}^2}{2}+\frac{{\eta }_1^2\left(\tau \right)}{2}-\frac{{\chi }^{\prime }}{3}{\eta }_1^3\left(\tau \right)+\frac{1}{4}{\eta }_1^4\left(\tau \right)$ (28)

另H = 0，则(28)可以化简为：

${\eta }_2^2={\left({{\eta }^{\prime }}_1\right)}^2=-{\eta }_1^2+\frac{2}{3}{\chi }^{\prime }{\eta }_1^3-\frac{1}{2}{\eta }_1^4$ (29)

对(29)求解可得：

$\frac{\text{d}{\eta }_1\left(\tau \right)}{\text{d}\tau }=\pm {\eta }_1\sqrt{-\frac{{\eta }_1^2}{2}+\frac{2}{3}{\chi }^{\prime }{\eta }_1-1}$，则 $\tau =\pm \left(\arcsin \frac{\frac{2}{3}{\chi }^{\prime }{\eta }_1-2}{\left|{\eta }_1\right|\sqrt{\frac{2}{3}{\chi }^{\prime }}-2}\right)$

令 $u=\frac{2}{3}{\chi }^{\prime }$， $v=\sqrt{{\left(\frac{2}{3}{\chi }^{\prime }\right)}^2-2}=\sqrt{u^2-2}$，则 $\tau =\pm \left(\arcsin \frac{u{\eta }_1-2}{v{\eta }_1}+C\right)$。

取C = 0，可以得到：

${\eta }_1\left(\tau \right)=\frac{2}{u\pm v\sin \tau }$， ${\eta }_2\left(\tau \right)=\frac{\mp 2v\cos \tau }{{\left(u\pm v\sin \tau \right)}^2}$

经验证：

$\left({\eta }_1\left(\tau \right),{\eta }_2\left(\tau \right)\right)=\left(\frac{2}{u+v\sin \tau },\frac{-2v\cos \tau }{{\left(u+v\sin \tau \right)}^2}\right)$

$\left({\eta }_1\left(\tau \right),{\eta }_2\left(\tau \right)\right)=\left(\frac{2}{u-v\sin \tau },\frac{2v\cos \tau }{{\left(u-v\sin \tau \right)}^2}\right)$

5. 研究平衡点处的稳定性

在不存在外激励情况下( $g^{\prime }=0$ )，可将方程(25)看作是：

$\{\begin{array}{l}{{\eta }^{\prime }}_1\left(\tau \right)={\eta }_2\left(\tau \right)\\ {{\eta }^{\prime }}_2\left(\tau \right)=-{\alpha }^{\prime }{\eta }_2\left(\tau \right)-{\eta }_1\left(\tau \right)+{\chi }^{\prime }{\eta }_1^2\left(\tau \right)-{\eta }_1^3\left(\tau \right)\end{array}$ (30)

令 $\{\begin{array}{l}{f}_1\left({\eta }_1,{\eta }_2\right)={\eta }_2\left(\tau \right)\\ f_2\left({\eta }_1,{\eta }_2\right)=-{\alpha }^{\prime }{\eta }_2\left(\tau \right)-{\eta }_1\left(\tau \right)+{\chi }^{\prime }{\eta }_1^2\left(\tau \right)-{\eta }_1^3\left(\tau \right)\end{array}$ ；

Jacobi矩阵是：

$\left[\begin{array}{cc}\frac{\partial f_1}{\partial {\eta }_1}& \frac{\partial f_1}{\partial {\eta }_2}\\ \frac{\partial f_2}{\partial {\eta }_1}& \frac{\partial f_2}{\partial {\eta }_2}\end{array}\right]=\left[\begin{array}{cc}0& 1\\ -1+2{\chi }^{\prime }{\eta }_1-3{\eta }_1^2& -{\alpha }^{\prime }\end{array}\right]$

显然在 $2\le {\chi }^{\prime }$ 有三平衡点， $\left(0,0\right),\left(\frac{{\alpha }^{″}}{2}\pm \sqrt{{\left(\frac{{\chi }^{\prime }}{2}\right)}^2-1},0\right)$。

以下依据Floquet指数来分析平衡点处的稳定性

1) 在平衡点是 $\left(0,0\right)$ 情况，Jacobi矩阵为 $\left[\begin{array}{cc}0& 1\\ -1& -{\alpha }^{\prime }\end{array}\right]$。

特征方程是 $\left|\begin{array}{l}0-\delta 1\\ -1-{\alpha }^{\prime }-\delta \end{array}\right|=0$，解得 ${\delta }_{1,2}=\frac{-{\alpha }^{\prime }\pm \sqrt{{\left({\alpha }^{\prime }\right)}^2-4}}{2}$。

在 $0<{\alpha }^{\prime }<2$ 的情况下， ${\delta }_{1,2}=\frac{-{\alpha }^{\prime }}{2}\pm i\sqrt{1-{\left(\frac{{\alpha }^{\prime }}{2}\right)}^2}$ 是不等的复数，复平面上有稳定交点，图3。

${\alpha }^{\prime }=0.5$ ${\chi }^{\prime }=2$

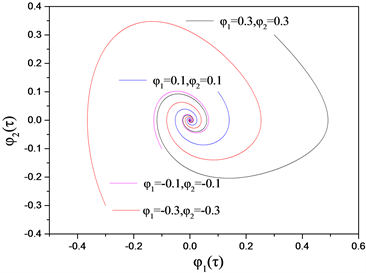
Figure 3. Phase diagram ( $0<{\alpha }^{\prime }<2$ )

图3. 相图( $0<{\alpha }^{\prime }<2$ )

在 ${\alpha }^{\prime }=2$ 的情况下， ${\delta }_{1,2}=-1$ 是相等负数，平衡点是临界结点，图4。

${\alpha }^{\prime }=2$ ${\chi }^{\prime }=2$

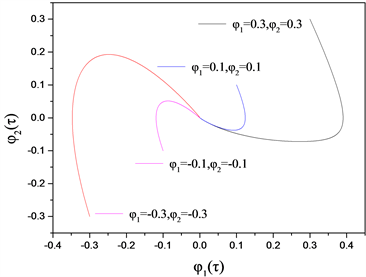
Figure 4. Phase diagram ( ${\alpha }^{\prime }=2$ )

图4. 相图( ${\alpha }^{\prime }=2$ )

在 ${\alpha }^{\prime }>2$ 的情况下， ${\delta }_{1,2}=-\frac{{\alpha }^{\prime }}{2}\pm \sqrt{{\left(\frac{{\alpha }^{\prime }}{2}\right)}^2-1}$ 是不等负数，平衡点是稳定结点，图5。

${\alpha }^{\prime }=4$ ${\chi }^{\prime }=2$

Figure 5. Phase diagram ( ${\alpha }^{\prime }>2$ )

图5. 相图( ${\alpha }^{\prime }>2$ )

在 ${\alpha }^{\prime }=0$ 的情况下， ${\delta }_{1,2}=\pm i$ 是纯虚数，求得曲线是极限环，图6。

${\chi }^{\prime }=2$

Figure 6. Phase diagram ( ${\alpha }^{\prime }=0$ )

图6. 相图( ${\alpha }^{\prime }=0$ )

2) 在平衡点 $\left(\frac{{\chi }^{\prime }}{2}+\sqrt{{\left(\frac{{\chi }^{\prime }}{2}\right)}^2-1},0\right)$ 处

Jacobi矩阵是 $\left[\begin{array}{cc}0& 1\\ \frac{4-{\left({\chi }^{\prime }\right)}^2-{\chi }^{\prime }\sqrt{{\left({\chi }^{\prime }\right)}^2-4}}{2}& -{\alpha }^{\prime }\end{array}\right]$，特征方程是 $\left|\begin{array}{l}0-\delta 1\\ 2-\frac{{\left({\chi }^{\prime }\right)}^2}{2}-\frac{{\chi }^{\prime }}{2}\sqrt{{\left({\chi }^{\prime }\right)}^2-4}-{\alpha }^{\prime }-\delta \end{array}\right|=0$，解得 ${\delta }_{1,2}=\frac{-{\alpha }^{\prime }\pm \sqrt{{\left({\alpha }^{\prime }\right)}^2+\left(8-2{\left({\chi }^{\prime }\right)}^2-2{\chi }^{\prime }\sqrt{{\left({\chi }^{\prime }\right)}^2-4}\right)}}{2}$。

在 $0<{\alpha }^{\prime }<\sqrt{-8+2{\left({\chi }^{\prime }\right)}^2-2{\chi }^{\prime }\sqrt{{\left({\chi }^{\prime }\right)}^2-4}}$ 情况下， ${\delta }_{1,2}=\frac{-{\alpha }^{\prime }}{2}\pm \frac{i}{2}\sqrt{-{\left({\alpha }^{\prime }\right)}^2-8+2{\left({\chi }^{\prime }\right)}^2+2{\chi }^{\prime }\sqrt{{\left({\chi }^{\prime }\right)}^2-4}}$ 是不等复数，复平面有稳定交点；

在 ${\alpha }^{\prime }=\sqrt{-8+2{\left({\chi }^{\prime }\right)}^2+2{\chi }^{\prime }\sqrt{{\left({\chi }^{\prime }\right)}^2-4}}$ 情况下， ${\delta }_{1,2}=-\frac{{\alpha }^{\prime }}{2}$ 是相等负数， $\left(\frac{{\chi }^{\prime }}{2}+\sqrt{{\left(\frac{{\chi }^{\prime }}{2}\right)}^2-1},0\right)$ 是临界结点；

在 ${\alpha }^{\prime }>\sqrt{-8+2{\left({\chi }^{\prime }\right)}^2+2{\chi }^{\prime }\sqrt{{\left({\chi }^{\prime }\right)}^2-4}}$ 情况下， ${\delta }_{1,2}=\frac{-{\alpha }^{\prime }\pm \sqrt{{\left({\alpha }^{\prime }\right)}^2-\left(8-2{\left({\chi }^{\prime }\right)}^2+2{\chi }^{\prime }\sqrt{{\left({\chi }^{\prime }\right)}^2-4}\right)}}{2}$ 是不等负数， $\left(\frac{{\chi }^{\prime }}{2}+\sqrt{{\left(\frac{{\chi }^{\prime }}{2}\right)}^2-1},0\right)$ 是稳定结点；

在 ${\alpha }^{\prime }=0$ 情况下，特征根 ${\delta }_{1,2}=\pm i\sqrt{-8+2{\left({\chi }^{\prime }\right)}^2+2{\chi }^{\prime }\sqrt{{\left({\chi }^{\prime }\right)}^2-4}}$ 是纯虚数，有Hopf分岔。

3) 在平衡点 $\left(\frac{{\chi }^{\prime }}{2}-\sqrt{{\left(\frac{{\chi }^{\prime }}{2}\right)}^2-1},0\right)$ 处

Jacobi矩阵 $\left[\begin{array}{cc}0& 1\\ \frac{4-{\left({\chi }^{\prime }\right)}^2+{\chi }^{\prime }\sqrt{{\left({\chi }^{\prime }\right)}^2-4}}{2}& -{\alpha }^{\prime }\end{array}\right]$， $\left(\frac{{\chi }^{\prime }}{2}-\sqrt{{\left(\frac{{\chi }^{\prime }}{2}\right)}^2-1},0\right)$ 处的特征根是 ${\delta }_{1,2}=\frac{-{\alpha }^{\prime }\pm \sqrt{{\left({\alpha }^{\prime }\right)}^2-8+2{\left({\chi }^{\prime }\right)}^2-2{\chi }^{\prime }\sqrt{{\left({\chi }^{\prime }\right)}^2-4}}}{2}$。 ${\delta }_{1,2}$ 是不等负数，平衡点是稳定结点。

6. 小结

1) S型波纹管非线性力学自由振动方程，准确解

$\left({\eta }_1\left(\tau \right),{\eta }_2\left(\tau \right)\right)=\left(\frac{2}{u+v\sin \tau },\frac{-2v\cos \tau }{{\left(u+v\sin \tau \right)}^2}\right)$

$\left({\eta }_1\left(\tau \right),{\eta }_2\left(\tau \right)\right)=\left(\frac{2}{u-v\sin \tau },\frac{2v\cos \tau }{{\left(u-v\sin \tau \right)}^2}\right)$

2) S型波纹管在动静载荷下，平衡点 $\left(0,0\right)$ 处，在 $0<{\alpha }^{\prime }<2$ 的情况下，根是不等复数，有稳定的交点；在 ${\alpha }^{\prime }=2$ 的情况下，根是相等负数，平衡点是临界点；在 ${\alpha }^{\prime }>2$ 的情况，根为不等负数，平衡点为稳定结点；在 ${\alpha }^{\prime }=0$ 的情况下，发生Hopf分岔。

基金项目

国家自然科学基金项目(11472123)，国家自然科学基金项目(11862012)。

NOTES

^*通讯作者。