考虑时滞因素的电力系统迭代辨识广域阻尼控制算法收敛性研究

Convergence Analysis of Algorithm for Iterative Identification Wide-Area Damping Control in Power System Considering Time Delay

摘要: 电力系统控制算法收敛性分析是衡量电力系统控制性能好坏的重要方法，算法收敛性决定了算法实现的可行性。迭代辨识算法是现代电力系统阻尼控制的一种重要控制方法，本文针对提出的一种考虑时滞的迭代辨识广域阻尼控制器算法，首先简述了该迭代辨识广域阻尼控制算法的基本步骤；其次把电力系统迭代辨识算法等效成分割系统，通过证明分割系统的稳定性间接证明了该算法的收敛性；然后又采用Q因子法分析了该算法的收敛速度；最后与其它方法在收敛速度上进行了对比，并分析了Vinnicombe的动态变化过程。仿真结果表明，本文提出的迭代辨识算法能在10秒内有效收敛，收敛速度较快。

Abstract: The convergence of power system algorithm is one of the indexes to measure the performance of power system algorithm. The convergence determines the feasibility of algorithm. The iterative identification algorithm is an important control method of modern power system control. In this paper, a new algorithm for iterative identification of wide-area damping controller is proposed. Firstly, the basic steps of the iterative identification wide-area damping control algorithm are briefly introduced. Secondly, the algorithm convergence is proved by using the method of segmentation system. Then, the convergence rate of the algorithm is analyzed by Q factor method. Finally, the convergence speed is compared with other methods. Simulation results show that the proposed algorithm can converge effectively and converge faster.

1. 引言

在电力系统阻尼控制领域应用的几十年内，提出了许多新的阻尼控制方法，其中迭代辨识与控制方法 [1] 取得了广泛的应用，迭代辨识方法的收敛性是电力系统控制算法能否应用的关键，是衡量电力系统算法性能的指标之一，若该算法发散，则无法辨识得到有效准确的系统模型，系统模型的响应会发生振荡，会恶化电力系统低频振荡的控制效果。因此，研究迭代辨识方法在电力系统广域阻尼控制中的收敛性问题是非常关键和有意义的。

算法收敛性分析的方法有很多种，有直接证明法，也有间接证明法，直接证明法是通过数学的方法直接对算法进行证明；间接证明法是通过分析算法对应的系统的稳定性，来间接证明算法的收敛性。此外还有概率法、定义法等等证明算法收敛性的方法。在二十世纪八十年代，学者们主要是利用数学工具来证明一些算法的收敛性，陈学敏等 [2] 通过数学知识，运用非线性数值分析理论推导出算法的收敛条件，从数学理论上证明了某些算法的收敛性与初值选取无关。二十一世纪乃至未来，随着整个科技的发展，数学工具仍然是分析算法收敛性的重要理论，刘铁男等 [3] 研究一、二阶P型迭代学习控制算法收敛条件，并对两种算法收敛速度进行比较。詹玉枝等 [4] 针对由二阶延迟微分方程刻画的系统过程，提出应用其基本解阵延迟正、余弦矩阵函数表达的精确解，设计迭代学习控制算法对系统进行输出跟踪控制，给出能使得延迟系统输出随迭代次数增加而收敛到给定期望输出的充分条件。Wijdeven等 [5] 提出鲁棒单调收敛性分析方法，该方法适用于有限时间区间内。吴涛 [6] 提出基于不同相关系数的双子群QPSO算法(Dual Group QPSO with Different Related Factors, DFR-QPSO)，该算法防止种群产生早熟现状，进而改善了QPSO的收敛性能。Ruan等 [7] [8] 针对收敛速度快慢的问题指出，在一定条件下，二阶迭代学习律比一阶控制律收敛速度快。邓集瀚 [9] 将细菌觅食(MBFO)算法应用到电力系统无功优化问题中，分析了MBFO的收敛速度快慢问题。Owens [10] 等指出POILC算法的特点，即计算量小，单调收敛。周伟等 [11] 充分利用实际系统中未知变量的已知边界条件和高阶内模规律，将最小二乘法与已知边界条件结合，解决系统中的多种非严格重复问题，在系统同时具有未知控制增益和扰动的情况下，所设计的控制律能保证跟踪误差的渐近收敛。罗彦博 [12] 提出了一种闭环超前型学习算法。Chien [13] 将高阶迭代学习控制算法与迭代算法信息的反馈控制相结合，设计的控制器增强了迭代控制器的稳定性。逄勃 [14] 提出一种优化迭代学习控制算法，该算法用来解决控制问题，能够实现单调递减。

上述关于算法及算法收敛性的讨论都从直接或间接的方向证明了算法的收敛性，也有从概率的方向证明了算法的收敛性，但是针对考虑时滞因素的迭代辨识方法的研究较少，因此本文针对一种考虑时滞的迭代辨识广域阻尼控制器算法，通过间接方法，把算法等效成分割系统来证明该算法的收敛性，并且对收敛速度进行了分析，从而验证算法实施的有效性。

2. 电力系统辨识模型与基本理论

2.1. 电力系统真实模型

参考电力系统实际运行情况，如图1所示，构造电力系统真实模型。图1所示模型用来研究电力系统闭环辨识问题。在真实系统中，以2个干扰信号为例，以此模拟随机性质小幅扰动 [15]。

Figure 1. Real model of closed-loop power system

图1. 闭环电力系统真实模型

图1中： $u\left(t\right)$ 和 $y\left(t\right)$ 分别表示系统的输入、输出信号， $t=1,2,\cdots$ $e_{10}\left(q\right)$ 和 $e_{20}\left(q\right)$ (均值为零、方差分别为 ${\lambda }_{10}$ 和 ${\lambda }_{20}$ )表示相关平稳随机干扰信号， $r\left(t\right)$ 表示与信号 $e_{10}\left(q\right)$ 和 $e_{20}\left(q\right)$ 独立的干扰信号， $G_{10}\left(q\right)$ 和 $G_{20}\left(q\right)$ 表示被控系统， $H_{10}\left(q\right)$ 和 $H_{20}\left(q\right)$ 分别表示干扰信号 $e_{10}\left(q\right)$ 和 $e_{20}\left(q\right)$ 的滤波器模型， $K_0\left(q\right)$ 表示控制器， $e^{-\tau \left(q\right)}$ 是时滞环节 [15]。

对于真实电力系统，闭环系统表达式可写为：

$\begin{array}{l}y\left(t\right)=S_0\left(q\right)G_0\left(q\right)r\left(t\right)+S_0\left(q\right)H_0\left(q\right)e_0\left(t\right)\\ u\left(t\right)=S_0\left(q\right)r\left(t\right)-S_0\left(q\right)F_0\left(q\right)e^{-\tau \left(q\right)}{H}_0\left(q\right)e_0\left(t\right)\end{array}$ (1)

其中 $S\left(q\right)={\left(1+G_0\left(q\right)F_0\left(q\right)e^{-\tau \left(q\right)}\right)}^{-1}$ 为灵敏度函数。

2.2. 电力系统辨识模型

利用如图2所示闭环电力系统辨识模型结构进行闭环辨识。

Figure 2. Identification model of closed-loop power system

图2. 闭环电力系统辨识模型

图2中： $u\left(t\right)$ 、 $y\left(t\right)$ 分别表示系统输入、输出信号， $e\left(q\right)$ (均值为零，方差为λ)表示随机干扰信号， $r\left(t\right)$ 表示外加参考信号， $G\left(q,\theta \right)$ 表示被控系统， $F\left(q,\theta \right)$ 表示控制器模型，θ表示待辨识模型参数， $t=1,2,\cdots$， $e^{-\tau \left(q,\theta \right)}$ 为时滞环节，τ为时滞值 [15]。

具体的形式类似真实电力系统，进一步写成如下形式：

$\begin{array}{l}y\left(t\right)=S\left(q,\theta \right)G\left(q,\theta \right)r\left(t\right)+S\left(q,\theta \right)H\left(q,\theta \right)e\left(t\right)\\ u\left(t\right)=S\left(q,\theta \right)r\left(t\right)-S\left(q,\theta \right)F\left(q,\theta \right)e^{-\tau \left(q,\theta \right)}H\left(q,\theta \right)e\left(t\right)\end{array}$ (2)

其中： $S\left(q,\theta \right)={\left(1+G\left(q,\theta \right)F\left(q,\theta \right)e^{-\tau \left(q,\theta \right)}\right)}^{-1}$ 为灵敏度函数。式(1)可改写为

$\left[\begin{array}{l}y\\ u\end{array}\right]=\left[\begin{array}{cc}\frac{G_0}{1+G_{0}F}& \frac{H_0}{1+G_{0}F}\\ \frac{1}{1+G_{0}F}& -\frac{H_{0}F}{1+G_{0}F}\end{array}\right]\left[\begin{array}{l}r\\ e\end{array}\right]$ (3)

电力系统模型G采用线性化状态空间模型为：

$\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)=Ax\left(t\right)+Bu\left(t-\tau \right)+Ee\left(t\right)\\ y\left(t\right)=Cx\left(t\right)+Du\left(t-\tau \right)\end{array}$ (4)

式中，x为系统的状态矢量，u、y分别表示被控系统输入、输出信号，e为外部扰动矢量，A、B、C、D、E为相应的系数矩阵。

2.3. 基本理论

定理1用来证明本算法的收敛性，以下三个引理用于定理1的证明。

引理1 [16] 对于任意的定常矩阵 $V\in R^{n\times n},V=V^{\text{T}}>0$，标量 $h>0$ 和向量函数 $\stackrel{\dot{}}{x}:\left[-h,0\right]\to R^n$，使得公式(5)的积分有定义，则以下不等式成立：

$-h{\displaystyle \underset{t-h}{\overset{t}{\int }}{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)V\stackrel{\dot{}}{x}\left(s\right)\text{d}s}\le {\zeta }_1^{\text{T}}\left(t\right)\left[\begin{array}{cc}-V& V\\ V& -V\end{array}\right]{\zeta }_1\left(t\right)$ (5)

$-\frac{h^2}{2}{\displaystyle \underset{-h}{\overset{0}{\int }}{\displaystyle \underset{t+\theta }{\overset{t}{\int }}{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)V\stackrel{\dot{}}{x}\left(s\right)\text{d}s}}\le {\zeta }_2^{\text{T}}\left(t\right)\left[\begin{array}{cc}-V& V\\ V& -V\end{array}\right]{\zeta }_2\left(t\right)$ (6)

其中， ${\zeta }_1^{\text{T}}\left(t\right)=\left[x^{\text{T}}\left(t\right)x^{\text{T}}\left(t-h\right)\right]$， ${\zeta }_2^{\text{T}}\left(t\right)=\left[x^{\text{T}}\left(t\right)x^{\text{T}}\left(t-h\right)\right]$。

引理2 [17] 设 $h_1<h\left(t\right)\le h_2$，其中 $h\left(t\right):R_{+}\to R_{+}$，对于任意的 $R=R^{\text{T}}>0$，如下不等式成立：

$\begin{array}{c}-{\displaystyle \underset{t-h_3}{\overset{t-h_2}{\int }}{\stackrel{\dot{}}{x}}^T\left(s\right)R\stackrel{\dot{}}{x}\left(s\right)\text{d}s}\le {\delta }^{\text{T}}\left(t\right)\{\left(h_3-h\left(t\right)\right)T{R}^{-1}{T}^{\text{T}}+\left(h\left(t\right)-h_2\right)Y{R}^{-1}{Y}^{\text{T}}\\ +\left[Y-Y+T-T\right]+{\left[Y-Y+T-T\right]}^{\text{T}}\}\delta \left(t\right)\end{array}$ (7)

其中，

${\delta }^{\text{T}}\left(t\right)=\left[x^{\text{T}}\left(t-h_1\right)x^{\text{T}}\left(t-h\left(t\right)\right)x^{\text{T}}\left(t-h_2\right)\right]$

$T={\left[T_1^{\text{T}}{T}_2^{\text{T}}{T}_3^{\text{T}}\right]}^{\text{T}}$, $Y={\left[Y_1^{\text{T}}{Y}_2^{\text{T}}{Y}_3^{\text{T}}\right]}^{\text{T}}$.

引理3 [18] 假设 ${\gamma }_1\le \gamma \left(t\right)\le {\gamma }_2$，其中 $\gamma (\cdot ):R_{+}\to R_{+}$，对于任意的适当维度的常数矩阵 ${\Xi }_1$ 、 ${\Xi }_2$ 和Ω，有以下矩阵不等式成立：

$\Omega +\left(\gamma \left(t\right)-{\gamma }_1\right){\Xi }_1+\left(\gamma \left(t\right){\gamma }_2-\gamma \left(t\right)\right){\Xi }_2<0$ (8)

当且仅当

$\Omega +\left({\gamma }_2-{\gamma }_1\right){\Xi }_1<0,\Omega +\left({\gamma }_2-{\gamma }_1\right){\Xi }_2<0$ (9)

3. 考虑时滞因素的迭代辨识广域阻尼控制算法步骤

时滞可分为两类，一类是常数时滞，一类是时变时滞。针对时变时滞问题，我们采用时滞上界，将时滞上界转化为常数时滞，从而进一步分析。对于式(4)所示的时滞线性系统，定义 $\bar{\tau }=\max \left(\tau \right)$，设计如下的时滞状态反馈控制器K。

$u\left(t-\tau \right)=Kx\left(t-\tau \right)$ (10)

那么闭环时滞系统为

$\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)=Ax\left(t\right)+BKx\left(t-\tau \right)+Ee\left(t\right)\\ y\left(t\right)=Cx\left(t\right)+DKx\left(t-\tau \right)\end{array}$ (11)

针对系统(11)，我们用文献 [11] 的方法来设计状态反馈控制器和反馈增益矩阵，状态反馈控制器和反馈增益矩阵分别用线性矩阵不等式和极点配置法来设计。

图3是考虑时滞迭代辨识广域阻尼控制器辨识模型。

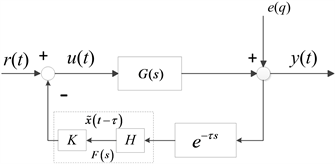
Figure 3. The identification model of wide-area damping controller considering time delay

图3. 考虑时滞迭代辨识广域阻尼控制器辨识模型

基于上述相关基本理论和定理，本文考虑时滞的迭代辨识与阻尼控制设计步骤如下：

第一步：给定降阶后开环系统对象模型G，初始控制器模型F(s)。

第二步：利用递推最小二乘法对模型G进行辨识，得到G的不确定性模型集合B_i。

第三步：将模型G转换为状态空间表达形式，确定模型G的状态空间各系数矩阵。

第四步：状态反馈控制器K利用LMI工具设计。

第五步：利用极点配置工具来设计反馈增益矩阵H。

第六步：根据第五步得到的状态反馈控制器K及反馈增益矩阵H，通过计算得到考虑时滞的控制器模型状态空间表达形式的各系数矩阵，从而得到考虑时滞的控制器模型传递函数。

第七步：根据频率稳定裕度公式，求取模型G_i与模型B_i对应的F(s)_i的频率稳定裕度 $b\left(G_i,F{\left(s\right)}_i\right)$。

第八步：根据Vinnicombe的相关理论，利用Vinnicombe公式求取标称模型G_i与模型集合B_i间的Vinnicombe距离 ${\delta }_v\left(G_i,B_i\right)$，并依次求取基于标称模型G_i的最大距离 ${\delta }_{WC}\left(G_i,B_i\right)$。

第九步：将频率稳定裕度 $b\left(G_i,F{\left(s\right)}_i\right)$ 与距离 ${\delta }_{WC}\left(G_i,B_i\right)$ 进行比较，筛选出满足 $b\left(G_i,F{\left(s\right)}_i\right)>{\delta }_{WC}\left(G_i,B_i\right)$ 的集合，若不满足则返回第二步。

第十步：根据第三步和第四步得到的 $b\left(G_i,F{\left(s\right)}_i\right)$， $\delta \left(G,B_i\right)$，判断是否满足公式

$\left|{\delta }_v\left(G,B_i\right)-{\delta }_v\left(G_i,B_i\right)\right|\le 0.05$ (12)

(判断两个距离之间的差值是不是在误差0.05以内，此值越小表示辨识精度越来越高)和

${\delta }_{v\min }\left(G,B_i\right)<0.05$ (13)

(将距离控制在0.05之内，此值越小则说明最终辨识得到的G_op越能逼近于G)，若不满足则返回第二步。

第十一步：判断是否满足给定的特征根稳定性判据，若不满足则返回第五步，若满足，则输出模型G_op及对应的控制器模型F(s)_op，最后得到与模型G的Vinnicombe距离最小的模型G_opt及对应的控制器模型F(s)_opt。

考虑时滞的迭代辨识广域阻尼控制器设计步骤流程图如图4所示：

Figure 4. The flow chart of algorithm for iterative identification wide area damping control considering time delay

图4. 考虑时滞因素的迭代辨识广域阻尼控制算法流程图

4. 收敛性分析

4.1. 收敛性证明

本文采用间接方法来证明算法的收敛性，即利用时滞分割的方法，首先将时滞区间进行分割来等效算法的收敛性分析，然后证明每个时滞区间的稳定性，最后推出整个系统的稳定性，从而证明算法的收敛性。具体方法如下：

设N为大于零的正整数， $h_i\left(i=1,2,\cdots ,N+1\right)$ 为标量，对时滞区间进行如下平均分割：

$h_m=h_1<h_2<\cdots <h_N<h_{N+1}=h_M$ (14)

用 $h_{\delta }$ 表示子区间 $\left[h_i,h_{i+1}\right]$ 的长度，即 $h_{\delta }=h_{i+1}-h_i=\left(h_M-h_m\right)/N$，则满足 $0\le h_m\le h\left(t\right)\le h_M,\stackrel{\dot{}}{h}\left(t\right)\le \mu ,\forall t\ge 0$ 时以下定理成立。

定理1 对于给定值 $h_m$ 和 $h_M$，如果存在矩阵 $P=\left[\begin{array}{ccc}{P}_{11}& P_{12}& P_{13}\\ \ast & P_{22}& P_{\text{23}}\\ \ast & \ast & P_{\text{33}}\end{array}\right]$， $Q_i$， $Z_i$， $R_i\left(i=2,3\right)$ $h_m$ (正定对称)和适当维度的矩阵 $T_a,Y_a\left(a=1,2,3\right)$，使得如下线性矩阵不等式成立：

$\left[\begin{array}{ccccccc}{\psi }_{11}& {\psi }_{12}& {\psi }_{13}& {\psi }_{14}& {\psi }_{15}& {\psi }_{16}& 0\\ \ast & {\psi }_{22}& {\psi }_{23}& {\psi }_{24}& {\psi }_{25}& {\psi }_{26}& h_{\delta }{Y}_1^{\text{T}}\\ \ast & \ast & {\psi }_{33}& {\psi }_{34}& {\psi }_{35}& {\psi }_{36}& h_{\delta }{Y}_2^{\text{T}}\\ \ast & \ast & \ast & {\psi }_{44}& {\psi }_{45}& {\psi }_{46}& h_{\delta }{Y}_3^{\text{T}}\\ \ast & \ast & \ast & \ast & {\psi }_{55}& {\psi }_{56}& 0\\ \ast & \ast & \ast & \ast & \ast & {\psi }_{\text{6}6}& 0\end{array}\right]<0,i=1,2,\cdots ,N$ (15)

$\left[\begin{array}{ccccccc}{\psi }_{11}& {\psi }_{12}& {\psi }_{13}& {\psi }_{14}& {\psi }_{15}& {\psi }_{16}& 0\\ \ast & {\psi }_{22}& {\psi }_{23}& {\psi }_{24}& {\psi }_{25}& {\psi }_{26}& h_{\delta }{T}_1^{\text{T}}\\ \ast & \ast & {\psi }_{33}& {\psi }_{34}& {\psi }_{35}& {\psi }_{36}& h_{\delta }{T}_2^{\text{T}}\\ \ast & \ast & \ast & {\psi }_{44}& {\psi }_{45}& {\psi }_{46}& h_{\delta }{T}_3^{\text{T}}\\ \ast & \ast & \ast & \ast & {\psi }_{55}& {\psi }_{56}& 0\\ \ast & \ast & \ast & \ast & \ast & {\psi }_{\text{6}6}& 0\end{array}\right]<0,i=1,2,\cdots ,N$ (16)

则系统是渐近稳定的。

其中，

${\psi }_{11}=P_{11}A+A^{\text{T}}{P}_{11}+P_{12}+P_{12}^{\text{T}}+Q_2+Q_3-Z_2-h_i^2{R}_2-h_{\delta }^2{R}_3+A^{\text{T}}MA$, ${\psi }_{13}=P_{11}B+A^{\text{T}}MB$,

${\psi }_{12}=Z_2-P_{12}+P_{13}$, ${\psi }_{14}=-P_{13}$, ${\psi }_{15}=A^{\text{T}}{P}_{21}+P_{22}^{\text{T}}+h_i{R}_2$, ${\psi }_{16}=A^{\text{T}}{P}_{31}+P_{32}^{\text{T}}+h_i{R}_3$,

${\psi }_{22}=-Q_2-Z_2+Y_1+Y_1^{\text{T}}$, ${\psi }_{23}=-Y_1+T_1+Y_2^{\text{T}}$, ${\psi }_{24}=-T_1+Y_3^{\text{T}}$, ${\psi }_{25}=-P_{22}^{\text{T}}+P_{23}^{\text{T}}$, ${\psi }_{26}=-P_{32}^{\text{T}}+P_{33}^{\text{T}}$,

${\psi }_{33}=-Y_2-Y_2^{\text{T}}+T_2+T_2^{\text{T}}+B^{\text{T}}MB$, ${\psi }_{34}=-T_2-Y_3^{\text{T}}+T_3^{\text{T}}$, ${\psi }_{35}=-B^{\text{T}}{P}_{21}^{\text{T}}$, ${\psi }_{36}=B^{\text{T}}{P}_{31}^{\text{T}}$,

${\psi }_{44}=-T_3-T_3^{\text{T}}-Q_3$, ${\psi }_{45}=-P_{23}^{\text{T}}$, ${\psi }_{46}=-P_{33}^{\text{T}}$, ${\psi }_{55}=-R_2$, ${\psi }_{56}=0$, ${\psi }_{66}=-R_3$,

$h_{\delta }=h_{i+1}-h_i=\left(h_M-h_m\right)/N$, $h_i=h_1+\left(i-1\right)\left(h_M-h_m\right)/N$,

$M=h_i^2{Z}_2+h_{\delta }{Z}_3+\frac{1}{4}\left[\left(h_i^4{R}_2\right)+{\left(h_{i+1}^2-h_i^2\right)}^2{R}_3\right].$

证明：首先证明 $h\left(t\right)\in \left[h_2,h_3\right]$ 子区间段时，定理成立，进而推广到 $h\left(t\right)\in \left[h_i,h_{i+1}\right]$ 时成立。

当满足 $h\left(t\right)\in \left[h_2,h_3\right]$ 时，构造Lyapunov-Krasovskii泛函：

$V_2\left(t\right)=V_{21}\left(t\right)+V_{22}\left(t\right)+V_{23}\left(t\right)$ (17)

其中，

$V_{21}\left(t\right)={\xi }_2^{\text{T}}\left(t\right)P{\xi }_2(\; t\; )$

$\begin{array}{l}{V}_{22}\left(t\right)={\displaystyle \underset{t-h_2}{\overset{t}{\int }}{x}^{\text{T}}\left(s\right)Q_{2}x\left(s\right)\text{d}s}+{\displaystyle \underset{t-h_3}{\overset{t}{\int }}{x}^{\text{T}}\left(s\right)Q_3{x}^{\text{T}}\left(s\right)\text{d}s}\\ +h_2{\displaystyle \underset{-h_2}{\overset{0}{\int }}{\displaystyle \underset{t+\theta }{\overset{t}{\int }}{\stackrel{\dot{}}{x}}^{\text{T}}}\left(s\right)Z_2\stackrel{\dot{}}{x}\left(s\right)\text{d}s\text{d}\theta }+{\displaystyle \underset{-h_3}{\overset{-h_2}{\int }}{\displaystyle \underset{t+\theta }{\overset{t}{\int }}{\stackrel{\dot{}}{x}}^{\text{T}}}\left(s\right)Z_3\stackrel{\dot{}}{x}\left(s\right)\text{d}s\text{d}\theta }\end{array}$

$V_{23}\left(t\right)=\frac{h_2^2}{2}{\displaystyle \underset{-h_2}{\overset{0}{\int }}{\displaystyle \underset{\theta }{\overset{0}{\int }}{\displaystyle \underset{t+\lambda }{\overset{t}{\int }}{\stackrel{\dot{}}{x}}^{\text{T}}}}\left(s\right)R_2\stackrel{\dot{}}{x}\left(s\right)\text{d}s\text{d}\lambda \text{d}\theta }+\frac{h_3^2-h_2^2}{2}{\displaystyle \underset{-h_3}{\overset{-h_2}{\int }}{\displaystyle \underset{\theta }{\overset{0}{\int }}{\displaystyle \underset{t+\lambda }{\overset{t}{\int }}{\stackrel{\dot{}}{x}}^{\text{T}}}}\left(s\right)R_3\stackrel{\dot{}}{x}\left(s\right)\text{d}s\text{d}\lambda \text{d}\theta }$

${\xi }_2^{\text{T}}\left(t\right)=\left[x^{\text{T}}\left(t\right){\displaystyle \underset{t-h_2}{\overset{t}{\int }}{x}^{\text{T}}\left(s\right)}{\displaystyle \underset{t-h_3}{\overset{t-h_2}{\int }}{x}^{\text{T}}\left(s\right)\text{d}s}\right]$

取Lyapunov-Krasovskii泛函 $V_2\left(t\right)$ 沿系统(11)的导数，有

${\stackrel{\dot{}}{V}}_2\left(t\right)={\stackrel{\dot{}}{V}}_{21}\left(t\right)+{\stackrel{\dot{}}{V}}_{22}\left(t\right)+{\stackrel{\dot{}}{V}}_{23}\left(t\right)$ (18)

其中， ${\stackrel{\dot{}}{V}}_{21}\left(t\right)=2{\xi }_2^{\text{T}}\left(t\right)P{\stackrel{\dot{}}{\xi }}_2\left(t\right)$，

$\begin{array}{l}{\stackrel{\dot{}}{V}}_{22}\left(t\right)=x^{\text{T}}\left(t\right)\left(Q_2+Q_3\right)x\left(t\right)-x^{\text{T}}\left(t-h_2\right)Q_2{x}^{\text{T}}\left(t-h_2\right)\\ -x^{\text{T}}\left(t-h_3\right)Q_2{x}^{\text{T}}\left(t-h_3\right)+x^{\text{T}}\left(t\right)\left[h_2^2{Z}_2+\left(h_3-h_2\right)Z_3\right]\stackrel{\dot{}}{x}\left(t\right)\\ -h_2{\displaystyle \underset{t-h_2}{\overset{t}{\int }}{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)Z_2\stackrel{\dot{}}{x}\left(s\right)\text{d}s}-{\displaystyle \underset{t-h_3}{\overset{t-h_2}{\int }}{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)Z_3\stackrel{\dot{}}{x}\left(s\right)\text{d}s}\end{array}$

$V_{23}\left(t\right)={\stackrel{\dot{}}{x}}^{\text{T}}\left(t\right)\left[\frac{1}{4}\left[\left(h_2^4{R}_2\right)+{\left(h_3^2-h_2^2\right)}^2{R}_3\right]\right]\stackrel{\dot{}}{x}\left(t\right)-\frac{h_2^2}{2}{\displaystyle \underset{-h_2}{\overset{0}{\int }}{\displaystyle \underset{t+\theta }{\overset{t}{\int }}{\stackrel{\dot{}}{x}}^{\text{T}}}}\left(s\right)R_2\stackrel{\dot{}}{x}\left(t\right)\text{d}s\text{d}\theta$

根据引理1可得

$-h_2{\displaystyle \underset{t-h_2}{\overset{t}{\int }}{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)Z_2\stackrel{\dot{}}{x}\left(s\right)\text{d}s}\le {\left[\begin{array}{c}x\left(t\right)\\ x\left(t-h_2\right)\end{array}\right]}^{\text{T}}\left[\begin{array}{cc}-Z_2& Z_2\\ \ast & -Z_2\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ x\left(t-h_2\right)\end{array}\right]$ (19)

$-\frac{h_2^2}{2}{\displaystyle \underset{-h_2}{\overset{0}{\int }}{\displaystyle \underset{t+\theta }{\overset{t}{\int }}{\stackrel{\dot{}}{x}}^{\text{T}}}}\left(s\right)R_2\stackrel{\dot{}}{x}\left(t\right)\text{d}s\text{d}\theta \le {\left[\begin{array}{c}{h}_{2}x\left(t\right)\\ {\displaystyle \underset{t-h_2}{\overset{t}{\int }}x\left(s\right)\text{d}s}\end{array}\right]}^{\text{T}}\left[\begin{array}{cc}-R_2& R_2\\ \ast & -R_2\end{array}\right]\left[\begin{array}{c}{h}_{2}x\left(t\right)\\ {\displaystyle \underset{t-h_2}{\overset{t}{\int }}x\left(s\right)\text{d}s}\end{array}\right]$ (20)

$\frac{h_3^2-h_2^2}{2}{\displaystyle \underset{-h_3}{\overset{-h_2}{\int }}{\displaystyle \underset{t+\theta }{\overset{t}{\int }}{\stackrel{\dot{}}{x}}^{\text{T}}}}\left(s\right)R_3\stackrel{\dot{}}{x}\left(t\right)\text{d}s\text{d}\theta \le {\left[\begin{array}{c}\left(h-3-h_2\right)x\left(t\right)\\ {\displaystyle \underset{t-h_3}{\overset{t-h_2}{\int }}x\left(s\right)\text{d}s}\end{array}\right]}^{\text{T}}\left[\begin{array}{cc}-R_3& R_3\\ \ast & -R_3\end{array}\right]\left[\begin{array}{c}\left(h-3-h_2\right)x\left(t\right)\\ {\displaystyle \underset{t-h_3}{\overset{t-h_2}{\int }}x\left(s\right)\text{d}s}\end{array}\right]$ (21)

由引理2可得：

$\begin{array}{c}-{\displaystyle \underset{t-h_3}{\overset{t-h_2}{\int }}{\stackrel{\dot{}}{x}}^{\text{T}}\left(s\right)Z_3\stackrel{\dot{}}{x}\left(s\right)\text{d}s}\le {\delta }^{\text{T}}\left(t\right)\{\left(h_3-h\left(t\right)\right)T{Z}_3^{-1}{T}^{\text{T}}+\left(h\left(t\right)-h_2\right)Y{Z}_3^{-1}{T}^{\text{T}}\\ +\left[Y-Y+T-T\right]+t{\left[Y-Y+T-T\right]}^{\text{T}}\}\delta \left(t\right)\end{array}$ (22)

将式(19)~(22)不等式右边代入(18)，则 ${\stackrel{\dot{}}{V}}_2\left(t\right)$ 可表示为

${\stackrel{\dot{}}{V}}_2\left(t\right)\le {\varsigma }^{\text{T}}\left(t\right)\left(\psi +\left(h_3-h\left(t\right)\right)T{Z}_3^{-1}{T}^{\text{T}}+\left(h\left(t\right)-h_2\right)Y{Z}_3^{-1}{T}^{\text{T}}\right)\varsigma \left(t\right)$ (23)

其中，

${\varsigma }^{\text{T}}\left(t\right)=\left[x^{\text{T}}\left(t\right)x^{\text{T}}\left(t-h_2\right)x^{\text{T}}\left(t-h\left(t\right)\right)x^{\text{T}}\left(t-h_3\right){\displaystyle \underset{t-h_2}{\overset{t}{\int }}{x}^T\left(s\right)\text{d}s}{\displaystyle \underset{t-h_3}{\overset{t-h_2}{\int }}{x}^{\text{T}}\left(s\right)\text{d}s}\right]$

如果对于 $h\left(t\right)\in \left[h_2,h_3\right]$，令 $\psi ={\left({\psi }_{i,j}\right)}_{6\times 6}$，有以下条件成立：

$\psi +\left(h_3-h\left(t\right)\right)T{Z}_3^{-1}{T}^{\text{T}}+\left(h\left(t\right)-h_2\right)Y{Z}_3^{-1}{T}^{\text{T}}<0$ (24)

则根据Lyapunov-Krasovskii稳定性定理 [15]，存在 $\epsilon >0$，满足 ${\stackrel{\dot{}}{V}}_2\left(t\right)<-\epsilon {\Vert x\left(t\right)\Vert }^2$，可进一步得出系统(11)是渐近稳定的。

根据引理3，式(24)等价于

$\psi +\left(h_3-h_2\right)T{Z}_3^{-1}{T}^{\text{T}}<0$ (25)

$\psi +\left(h_3-h_2\right)Y{Z}_3^{-1}{Y}^{\text{T}}<0$ (26)

根据schur补知，式(29)和(30)分别等价于当i = 2时的(25)和(26)。

因此，当 $h\left(t\right)\in \left[h_i,h_{i+1}\right]\left(i-1,2,\cdots ,N\right)$ 时，可构造如下Lyapunov-Krasovskii泛函：

$V_i\left(t\right)=V_{i1}\left(t\right)+V_{i2}\left(t\right)+V_{i3}\left(t\right)$ (27)

同理可证得当 $h\left(t\right)\in \left[h_i,h_{i+1}\right]$ 时，有 $\stackrel{\dot{}}{V}\left(t\right)<-\epsilon {\Vert x\left(t\right)\Vert }^2$，由此可知系统(11)是渐近稳定的。

定理证毕。 □

4.2. 基于Q因子的迭代辨识算法收敛速度分析

基于Q因子的迭代辨识算法收敛速度分析如下：

考虑如(28)所示的系统，

$\{\begin{array}{l}\stackrel{\dot{}}{x}=Ax+bu\\ y=cx+du\end{array}x\left(0\right)=x_0$ (28)

x、u、y分别表示系统的状态，输入和输出。A是未知的矩阵，b和c是未知矢量，d是未知标量， $\text{0}<{\alpha }_1\le d\le {\alpha }_2$， ${\alpha }_1$ 和 ${\alpha }_{\text{2}}$ 是已知的常数。

每次迭代辨识过程系统如(29)所示。

$\Re :\{\begin{array}{l}{\stackrel{\dot{}}{x}}_i=A{x}_i+b{u}_i\\ y_i=c{x}_i+d{u}_i\end{array}{x}_i\left(0\right)=x_0$ (29)

控制目标就是去寻找一个控制输入序列使输出y_i(t)能够追踪期望输出y_d(t)，即，随着迭代次数增加，系统输出能够收敛到期望输出。令 $\underset{i\to \infty }{\lim }\left|\Delta y_i\right|=0$，其中， $\Delta y_i\left(t\right)=y_d\left(t\right)-y_i\left(t\right)$。Q因子定义为：

$Q_p=\underset{i\to \infty }{\lim }\sup \frac{\left|\Delta y_{i+1}\right|}{{\left|\Delta y_i\right|}^p}$ (30)

迭代学习的控制机制为：

$u_{i+1}\left(t\right)=p_1{u}_i+p_2{u}_{i-1}+q_1\Delta y_i+q_2\Delta y_{i-1}$ (31)

其中， $p_1+p_2=1$， $q_1$ 和 $q_2$ 是常数，满足 $\left|p_1-q_{1}d\right|+\left|p_2-q_{2}d\right|<1$，在文献 [18] 中已证明随着迭代次数i趋向于无穷大，跟踪误差是收敛的，且得到 ${\left|\Delta y_{i-1}\right|}_{\lambda }\le \left|p_1-q_{1}d\right|{\left|\Delta y_i\right|}_{\lambda }+\left|p_2-q_{2}d\right|{\left|\Delta y_{i-1}\right|}_{\lambda }$，根据Q因子的定义公式(30)，得到：

$Q=\underset{i\to \infty }{\lim }\sup \frac{{\left|\Delta y_{i+1}\right|}_{\lambda }}{{\left|\Delta y_i\right|}_{\lambda }}={\gamma }_1+{\gamma }_2\underset{i\to \infty }{\lim }\frac{{\left|\Delta y_{i-1}\right|}_{\lambda }}{{\left|\Delta y_i\right|}_{\lambda }}$ (32)

其中， ${\gamma }_1=\left|p_1-q_{1}d\right|$， ${\gamma }_2=\left|p_2-q_{2}d\right|$，迭代学习控制的特征方程为：

$z^2-\left|p_1-q_{1}d\right|z-\left|p_2-q_{2}d\right|=0$ (33)

用g₁，g₂表示方程(33)的根，

$g_1=\frac{{\gamma }_1-\sqrt{{\gamma }_1^2+4{\gamma }_2}}{2}$， $g_{\text{2}}=\frac{{\gamma }_1\text{+}\sqrt{{\gamma }_1^2+4{\gamma }_2}}{2}$ (34)

因为 $\left|g_2\right|\ge \left|g_1\right|$，因此Q因子由 $g_2$ 决定，我们将迭代辨识过程构造为如下最优问题：

$J=\underset{p\in R}{\min }\underset{\left(q_1,q_2\right)\in R^2}{\min }\underset{d\in D}{\max }\frac{{\gamma }_1\text{+}\sqrt{{\gamma }_1^2+4{\gamma }_2}}{2}$ (35)

因此给出如下定理：

定理2：最优问题(35)的解是 $J=\theta =\frac{{\alpha }_2-{\alpha }_1}{{\alpha }_2+{\alpha }_1}$，当 $p_{\text{1}}=\text{1}$, $p_{\text{2}}=0$, $q_1=\frac{2}{{\alpha }_2+{\alpha }_1}$, $q_{\text{2}}=0$ 时取得最优值，收敛速度达到最大。

证明：将p₁范围分为3部分，分别计算目标函数。

1) $p_1\le 0$，令 $J_a\left(p_1\right)=\underset{\left(q_1,q_2\right)\in R^2}{\min }\underset{d\in D}{\max }{g}_2$，且 $J_A=\underset{p_{\text{1}}\in \left(-\infty ,0\right)}{\min }{J}_a\left(p_1\right)$。由文献 [19] 可以得到：

$\underset{q_1\in R}{\min }\underset{d\in D}{\max }\left|p_1-q_1{d}_1\right|=\left|p_1\theta \right|=-p_1\theta$， $q_{1,a}=\frac{2}{{\alpha }_2+{\alpha }_1}$ (36)

我们得到

$J_a\left(p_1\right)=\frac{-p_1\theta +\sqrt{p_1^2{\theta }^2+4\left(1-p_1\right)\theta }}{\text{2}}$ (37)

取关于p₁的偏导，得到

$\frac{\partial J_a\left(p_1\right)}{\partial \left(p_1\right)}=-\frac{\theta }{2}+\frac{p_1{\theta }^2-2\theta }{2\sqrt{p_1^2{\theta }^2+4\left(1-p_1\right)\theta }}<0$ (38)

由此可得当 $p_1\in \left(-\infty ,0\right]$， $J_a\left(p_1\right)$ 是单调递减的，因此当 $p_1=0$ 时，取得最小值 $J_A=\underset{p_1\in \left(-\infty ,0\right)}{\min }{J}_a\left(0\right)=\sqrt{\theta }$。

2) $\text{0}<p_1\le \text{1}$ 令 $J_b\left(p_1\right)=\underset{\left(q_1,q_2\right)\in R^2}{\min }\underset{d\in D}{\max }{g}_2$，且 $J_B=\underset{p_{\text{1}}\in \left(-\infty ,0\right)}{\min }{J}_b\left(p_1\right)$。由文献 [19] 可以得到：

$\underset{q_1\in R}{\min }\underset{d\in D}{\max }\left|p_1-q_1{d}_1\right|=\left|p_1\theta \right|=-p_1\theta$， $q_{1,b}=\frac{2}{{\alpha }_2+{\alpha }_1}$ (39)

我们得到

$J_b\left(p_1\right)=\frac{p_1\theta +\sqrt{p_1^2{\theta }^2+4\left(1-p_1\right)\theta }}{\text{2}}$ (40)

取关于p₁的偏导，得到

$\frac{\partial J_b\left(p_1\right)}{\partial \left(p_1\right)}=\frac{\theta }{2}+\frac{p_1{\theta }^2-2\theta }{2\sqrt{p_1^2{\theta }^2+4\left(1-p_1\right)\theta }}<0$ (41)

由此可得当 $p_1\in \left(\text{0},\text{1}\right]$， $J_b\left(p_1\right)$ 是单调递减的，因此当 $p_1=1$ 时，取得最小值 $J_B=\underset{p_1\in \left(0,1\right]}{\min }{J}_b\left(1\right)=\theta$。

3) $p_1>1$ 令 $J_c\left(p_1\right)=\underset{\left(q_1,q_2\right)\in R^2}{\min }\underset{d\in D}{\max }{g}_2$，且 $J_C=\underset{p_{\text{1}}\in \left(1,-\infty \right)}{\min }{J}_c\left(p_1\right)$。由文献 [19] 可以得到：

$\underset{q_1\in R}{\min }\underset{d\in D}{\max }\left|p_1-q_1{d}_1\right|=\left|p_1\theta \right|=p_1\theta$ (42)

我们得到

$J_c\left(p_1\right)=\frac{p_1\theta +\sqrt{p_1^2{\theta }^2+4\left(1-p_1\right)\theta }}{\text{2}}$ (43)

取关于p₁的偏导，得到

$\frac{\partial J_c\left(p_1\right)}{\partial \left(p_1\right)}=\frac{\theta }{2}+\frac{p_1{\theta }^2-2\theta }{2\sqrt{p_1^2{\theta }^2+4\left(1-p_1\right)\theta }}>0$ (44)

由此可得当 $p_1\in \left(\text{1,}\infty \right)$， $J_b\left(p_1\right)$ 是单调递增的，因此当 $p_1=1$ 时，取得最小值 $J_C=\underset{p_1\in \left(1,\infty \right)}{\min }{J}_c\left(1\right)=\theta$。

所以 $J=\min \left\{J_A,J_B,J_C\right\}=\theta$。

定理证毕。 □

4.3. 收敛速度仿真

4.1节及4.2节是对算法进行收敛性及收敛速度的理论分析，本节是从实际仿真角度来验证算法的收敛性及收敛速度。图5为本文与其它算法在四机两区系统模型上的收敛速度对比图。为了更清晰地分析本算法的收敛性，我们从Vinnicombe距离 [20] 的角度来衡量本文算法的收敛性。闭环电力系统模型G与不确定性模型集合B_i之间的Vinnicombe距离曲线如图6所示。

Figure 5. Comparison of convergence rates for different algorithms

图5. 不同算法收敛速度对比图

三种控制器设计算法的收敛速度对比如图5所示，由图5可知，三种算法收敛速度排序为：本文 >文献 [21] > 文献 [22]，且在收敛时间上，本文 < 文献 [21] < 文献 [22]。通过分析可得：与其它两个算法相比，在达到同样误差条件下，本文所设计的时滞控制器设计算法能在10秒内有效收敛，收敛速度相对来说是较快的。

Figure 6. Vinnicombe distance between G and B_i

图6. G与B_i间的Vinnicombe距离

图6是Vinnicombe距离曲线变化图，它反映了电力系统降阶模型G与不确定模型集合B_i之间距离在迭代辨识过程中的变化关系，图6表明得到的辨识模型与G之间的距离的趋势是越来越小的，在第15次辨识的时候由于误差因素出现距离突变，最终G与B_i之间的Vinnicombe距离固定在0.01059。因此说明，根据本辨识及控制器设计算法，从Vinnicombe距离的角度来说，本算法是收敛的，可以得到有效的电力系统模型。

5. 结论

针对电力系统低频振荡阻尼控制问题，提出一种考虑时滞的迭代辨识广域阻尼控制器算法，并给出该迭代辨识广域阻尼控制算法的基本步骤，通过使用该算法可以准确有效地获得电力系统模型，采用分割系统的方法间接证明该算法收敛性，并采用Q因子法分析了算法的收敛速度。通过与其它两种常用方法进行对比的仿真结果表明，本文提出的迭代辨识算法能在10秒内有效收敛，收敛速度较快。

基金项目

清华大学电力系统及大型发电设备安全控制与仿真国家重点实验室基金(项目号：SKLD20M17)；北京市高等教育学会项目(项目号：YB2021131)；北京建筑大学金字塔人才培养工程(项目号：JDYC20200324)；北京建筑大学研究生教育教学质量提升项目(项目号：J2019001)；北京建筑大学教育科学研究重点项目(项目号：Y19-12)；北京建筑大学社会实践与创新创业课程项目(项目号：SJSC1913)；国家自然科学基金委青年科学基金项目(项目号：51407201)。