基于周期性多态洗衣机运行的混合事件检测算法

Hybrid Event Detection Algorithm Based on Periodic Polymorphic Washing Machine Operation

摘要: 事件检测是非侵入式负荷监测与识别的重要环节。针对洗衣机运行时存在多事件无法识别的问题，本文提出了基于周期性多态洗衣机运行的混合事件检测算法，先采用CUSUM算法捕捉启停波形，引入shapeDTW算法对其中的周期性波形进行匹配识别，并将其从总负荷数据中剥离，避免周期性波形对其他电器事件检测的影响，该方法能具有很高的识别未知周期性波形的自适应能力。在多态洗衣机参与运行的情况下，投切各种特性负荷进行仿真分析、方法对比，该算法保证了特征提取的准确性，具有很高的检测精度，为事件检测算法的优化提供了借鉴意义。

Abstract: Event detection is an important part of non-intrusive load monitoring and identification. Aiming at the problem that multiple events cannot be recognized during the operation of washing machine, this paper proposes a mixed event detection algorithm based on the operation of periodic polymorphic washing machine. Firstly, the start and stop waveform is captured by the CUSUM algorithm, and the shapeDTW algorithm is introduced to match and identify the periodic waveform, and it is stripped from the total load data. The method can avoid the influence of periodic waveform on the detection of other electrical events and has high adaptive ability to identify unknown periodic waveform. In the case of multi-state washing machine participating in the operation, the simulation analysis and method comparison of various characteristic loads are carried out. The algorithm ensures the accuracy of feature extraction and has high detection accuracy, which provides a reference for the optimization of event detection algorithm.

1. 引言

负荷监测分为非侵入式和侵入式两种。非侵入式负荷监测 [1] (Non-intrusive Load Monitoring, NILM)旨在监视设备打开、关闭操作、工作时间以及其他相关信息。NILM将总功耗分解为单个设备的功耗，与侵入式负荷监测相比具有低成本，易于安装、拆卸和维护的优点。NILM主要包含3个步骤，分别是事件检测、特征提取和负荷识别。其中特征提取和负荷识别两部分均以事件检测为基础，因此，保证事件检测的准确性是NILM监测的关键之处。

目前事件检测主要分为两类：启发式方法和概率模型方法。第一类算法基于直观或经验，制定规则对信号突变时刻进行检测。在文献 [2] 中，通过计算两个连续样本点之间差值的绝对值来检测总有功功率信号中的事件，然后将其与预定义阈值进行比较。由于事件检测的多样性和差异性，依靠直观经验得到的检测结果漏检率、误检率较高，因而启发式方法应用较少 [3]。基于概率模型的事件检测方法检测一个序列中元素的分布或分布参数中某个变化发生的时刻，本质上为一种统计学判断假设的问题。在NILM的背景下，主要有4种方法用于检测电气量信号的变化：广义似然比(Generalized Likelihood Ratio Test, GLRT)、卡方拟合优度、贝叶斯信息准则(Bayesian Information Criterion, BIC)和累计和(Cumulative Sum, CUSUM)方法。GLRT是通过从平均值潜在变化前后的对数概率分布比率中导出一个决策函数来检测新事件的发生 [4] [5] [6]。卡方拟合优度是通过判断两个相邻窗口是否共享同一个分布来检测事件 [7] [8] [9]。BIC是通过将观测到的随机样本序列划分成均匀片段，使用模型复杂度惩罚的似然准则函数进行事件判断 [10] [11]。CUSUM算法是通过判断累计和是否超过阈值来检测事件 [12] [13] [14]。两类方法的结合使用可能会产生更好的结果，文献 [15] 运用混合算法依次消除了错误事件，解决了事件检测背景下高波动、瞬态时间长的问题。文献 [16] 依次使用不同类型的事件检测器来解决“检测噪声”的干扰。

上述事件检测是在“每次最多只有一个负荷发生状态变化”的假设基础上进行的 [17]，该假设被称为开关连续性原则SCP (Switch Continuity Principle) [1]。SCP与用户内部的负荷使用者数量、负荷数量、采样频率等因素有关 [18]，含周期性波形的多个负荷同时发生状态变化时，负荷特征难以提取，导致SCP不成立，严重影响负荷分解的结果。如洗衣机、电磁炉和微波炉等。因此，本文提出了一种针对洗衣机运行的混合事件检测方法。先采用CUSUM算法捕捉启停波形，引入shapeDTW算法对其中的周期性波形进行匹配识别，并将其从总负荷数据中剥离，再采用CUSUM算法对剥离后的总负荷数据重新检测。建立了自适应周期性波形数据库，提高了算法对未知周期性负荷的识别。通过实验验证该方法的有效性。

2. 多负荷同时发生状态变化

负荷运行时可能会有多种工作状态，比如洗衣机洗涤、甩干会产生周期性波形从而产生多个事件，如图1所示。洗衣机一个完整洗涤波形约为1 s，间隔约为1 s。此时打开其他电器，在2 s时间间隔内，至少有2个电器同时发生状态改变。

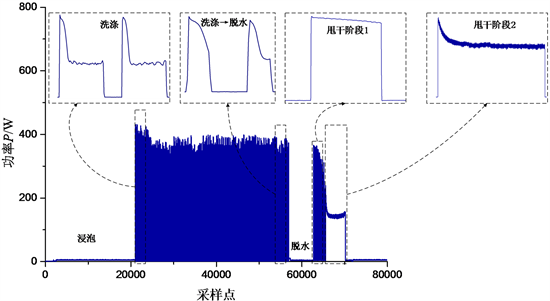
Figure 1. The power curve of washing machine operation

图1. 洗衣机运行的功率曲线

根据试验分析可知，电器波形的产生与实际工作机制有关。由于洗衣机是间歇式运行的，所以会产生周期性波形。基于这一特点，可通过单独识别周期性波形并剥离，再重新进行事件检测，最终避免洗衣机对其他电器的影响。

3. 混合事件检测算法

3.1. CUSUM事件检测算法

设有一电流有效值(简称电流)时间序列 $I={\left\{i\left(j\right)\right\}}_{j=1}^{\infty }$，定义两个连续的滑动窗口W_m (均值计算窗)和W_d (暂态检测窗)，其长度分别为m和n。分别计算两个窗口内的均值M_m和M_d，如式(1)、式(2)：

$M_m=\frac{{\displaystyle \underset{j=k}{\overset{k+m-1}{\sum }}i}\left(j\right)}{m}$ (1)

$M_d=\frac{{\displaystyle \underset{j=k+m}{\overset{k+m+n-1}{\sum }}i}\left(j\right)}{n}$ (2)

式中：k为时间序列的第一个采样点。

再分别定义 $g_k^{+}$ 和 $g_k^{-}$ 用于检测事件投入和切除，其计算方式如式(3)、式(4)所示：

$g_k^{+}=\max \left\{0,g_{k-1}^{+}+M_d-\left(M_m+\beta \right)\right\},g_0^{+}=0$ (3)

$g_k^{-}=\max \left\{0,g_{k-1}^{-}-M_d+\left(M_m-\beta \right)\right\},g_0^{-}=0$ (4)

式中： $\beta$ 为外界引入的噪声，表示该电流时间序列电流稳定时的波动水平。

以投入事件为例，令 $g_0^{+}=0$，当检测窗口均值M_d大于 $M_m+\beta$ 时， $g_k^{+}$ 开始大于零。根据检测需求设置累计和阈值H，当 $0<g_k^{+}<H$ 时，说明有事件发生的可能，但是累计的变化量尚未达到确定事件发生的程度，此时引入时间延迟因子d (初始值为0)，当 $0<g_k^{+}<H$ 时，令 $d=d+\text{1}$，计算 $g_{k+d}^{+}$，直至 $g_{k+d}^{+}>H$，则发生的时刻可根据 $t=k-d$ 倒推得出。为了避免序列震荡导致的事件多识别，引入时间延迟因子后，延迟因子每增加1，都要对 $g_{k+d}^{+}$ 和 $g_{k+d-1}^{+}$ 进行比较，如果 $g_{k+d}^{+}\le g_{k+d-1}^{+}$，则认为此时是波动引起的电流变化，并令 $g_{k+d}^{+}=0,d=0$，从而避免了由数据波动导致的多识别事件。以负荷投入事件检测为例的滑动窗双边CUSUM事件检测流程见附图1，检测切除事件的流程与此相似，不再累赘。

滑动窗口大小会影响CUSUM检测的灵敏度，窗口大可以有效避开尖峰的影响，但对样本点不够灵敏，是因为窗口累计和减小，导致漏测。应根据不同负荷特征，设置窗口大小。

3.2. shapeDTW算法

动态时间规整算法(Dynamic time warping, DTW)是一种在两个时间序列之间搜索最佳比对的方法。它用一个距离来度量测量和样本序列之间的相似性。由于序列在时间维度上出现局部非线性失真，而采用DTW可以很好地解决局部扭曲问题。

设时间序列X、Y的长度分别为M、N，即 $X=\left\{x_1,x_2,\cdots ,x_M\right\}$， $Y=\left\{y_1,y_2,\cdots ,y_N\right\}$。构造成对距离矩阵代价矩阵 $C^{M\times N}$，其中 $C\left(i,j\right)$ 是x_i和y_j的距离 $d_{ij}={\Vert y_j-x_i\Vert }_2$， ${\Vert \cdot \Vert }_2$ 表示2范数。

设X和Y之间的时间弯曲路径为

$p=\left(p_1,p_2,\cdots ,p_k,\cdots ,p_l\right)$ (5)

其中， $p_k=\left(i_k,j_k\right)\in \left\{1,2,\cdots ,i\right\}\times \left\{1,2,\cdots ,j\right\}$。

计算距离时需要满足边界性，连续性和单调性三个原则，如式(6)所示。

$\{\begin{array}{l}{p}_1=\left(1,1\right),p_l=\left(i,j\right)\\ i_1\le i_2\le \cdot \cdot \cdot \le i_l,j_1\le j_2\le \cdot \cdot \cdot \le j_l\\ p_{k+1}-p_k\in \left\{\left(1,1\right),\left(0,1\right),\left(1,0\right)\right\}\end{array}$ (6)

两个序列若要得到最佳的匹配，需要从代价矩阵的起点(1, 1)和终点(M, N)之间找到一条路径来获得最小的累计距离。

根据式(7)所示的递推规则，用动态规划算法搜索满足上述约束条件的X和Y之间的最优匹配路径，并计算出相应的最小累计距离D(M, N)，则X和Y之间的DTW距离可以定义为 $\text{DTW}\left(X,Y\right)=D\left(M,N\right)/L$，其中L是最优匹配路径的长度。

$D\left(i,j\right)=C\left(i,j\right)+\min \left\{D\left(i-1,j\right),D\left(i-1,j-1\right),D\left(i,j-1\right)\right\}$ (7)

根据上述原理，DTW算法在寻找最佳匹配路径的同时对齐两个时间序列的数据点，使得它们之间的“距离”最小化，例如图2所示。

DTW算法在某些约束条件下找到了全局最优的匹配，但它不一定能实现局部合理的匹配。因此在实际应用时会存在一定的误判情况，原因之一是因为DTW算法为寻求全局最优解而过度拉伸和缩放 [19]，如附图2(a)所示。为了解决这个问题，本文引入了shapeDTW算法 [20]。shapeDTW算法先针对每个时序数据点，利用其前序和后序的部分数据提取出其局部形态特征，再将每个点周围的局部形状信息结合到动态规划匹配过程中，从而产生更正确的对齐结果，即具有相似局部形状的点倾向于被匹配，而具有不相似领域的点不太可能被匹配。相比于标准的DTW算法只关注全局最优解，shapeDTW算法更加关注时间序列在局部形态特征上的匹配长度。由此可见，shapeDTW算法可以利用局部形态特征，在很大程度上避免了过度拉伸和缩放所导致的误判问题。

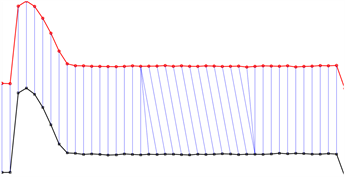
Figure 2. DTW algorithm principle schematic diagram

图2. DTW算法原理示意图

3.3. 建立自适应周期性波形数据库

3.3.1. 波形聚类

通过k-mean聚类方法对周期性波形进行聚类。考虑到聚类的对象是时间序列，时间序列可能长度不同。因此采用DTW距离代替欧式距离作为样本间的相似度度量标准。两个向量DTW距离越近则两个向量相似性越高，划分为同一类的可能性越高，否则相似性越低，划分为同一类的可能性越低。假设待聚类的样本集为 $Z=\left\{z_i|i=1,2,\cdots ,n\right\}$，待聚类样本集实际类数为K。聚类误差平方和如式(8)所示。

$E={\displaystyle \underset{i=1}{\overset{K}{\sum }}{\displaystyle \underset{j\in C_i}{\overset{}{\sum }}\text{DTW}\left(z_j-m_i\right)}}$ (8)

其中，C_i是第i类的所有样本。m_i是第i类的聚类中心。 ${\displaystyle {\sum }_{j\in C_i}\text{DTW}\left(z_j-m_i\right)}$ 表示第i类的所有样本到该聚类中心的DTW距离之和，该值越小，说明该类样本的相似性越高，聚类效果越好。

为了保证shapeDTW算法的有效性，需建立周期性波形数据库。本文采用改进k_means聚类算法对电器的工作波形进行聚类，将离聚类中心最近的波形作为该电器的典型波形。如图1所示，以洗衣机为例，洗衣机具有四类典型波形，设置聚类数量为4。本文建立的周期性波形数据库共有6种波形，见附图3。

3.3.2. 自适应周期性波形数据库

为保证周期性波形数据库的构建方法对于多数独立用户具有普适性，在聚类方法中，依据周期性负荷具有的操作特性对分类判别条件进行设定，从而实现对周期波形的无监督分类问题。

根据shapeDTW的原理只能将待测波形分配到已知的类别中，但是待测波形可能属于新出现的周期性波形，该待测波形与已知的类别相似度很小，因此可以预设一个阈值T，来识别新出现的周期性波形。自适应建立波形数据库步骤为：1) 待测波形z与周期性波形数据库的距离满足 $\text{DTW}\left(z,z_i\right)\le T$ 的最小值所对应的类别就判定该波形为哪一类。2) 若 $\text{DTW}\left(z,z_i\right)>T$，则将待测样本暂时判定为新出现的波形类别z_new，并暂时加入周期性波形数据库。3) 继续匹配下一个波形，如连续出现3个波形都匹配为z_new，则认为切入了周期性设备z_new，并永久将z_new加入周期性波形数据库。反之，则删除z_new。

3.4. 混合事件检测算法流程

本文共用到两次CUSUM检测，记为CUSUM_1和CUSUM_2。

1) 输入总负荷电流数据。通常事件检测考虑电流与功率特征，由于电流数据更加稳定，本文取电流为被检测的电气量。

2) 检测启停波形。CUSUM_1用于检测周期性波形的启停，由于洗衣进周期性波形的启停间隔较短，因此需设置较小的窗口。

3) 识别周期性波形。将2)中检测到的启停波形进行shapeDTW匹配，若出现连续3次波形匹配为同一个电器，则认为此时打开了该电器。当判断有周期性波形设备打开时，则将同类波形删除，即将连续检测到的启–停位置之间的数据剥离。最后，将各个片段重新连接成一个新的时间序列。

4) 检测其他电器波形。CUSUM_2用于检测3)处理后的数据。此时可认为无周期性电器运行，即SCP成立。因此窗口设置较大。具体设置可参考案例中电器的事件间隔大小。

本文提出的混合事件检测算法流程图如图3所示。

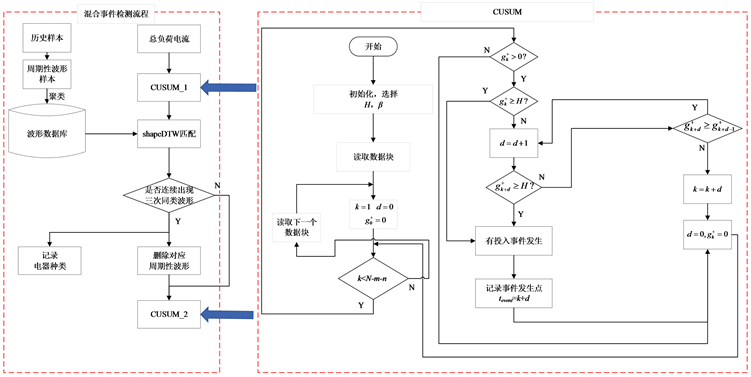
Figure 3. Mixed event detection algorithm flow chart

图3. 混合事件检测算法流程图

4. 试验与分析

4.1. 参数设置

4.1.1. 窗口设置

CUSUM_1负责检测周期负荷事件，窗口长度设置较小，取均值计算窗口长度m为2，检测窗口长度n为2。本算例除洗衣机外，事件发生间隔大多数在50个采样点以上，因此CUSUM_2窗口长度设置为50，取均值计算窗口长度m为40，检测窗口长度n为10。shapeDTW算法中形状特征采用一维的梯度直方图 [20]。对比算法CUSUM和GLR算法的窗口均设置为50。

4.1.1. 阈值设置

设CUSUM的阈值为H，GLR的阈值为h。本节CUSUM_1、CUSUM_2的阈值H₁、H₂分别设置为1和3.5，对比算法CUSUM，GLR的阈值分别为H₃ = 3.5，h = 2。shapeDTW的阈值T设置为185。H、h、T的取值可通过训练获得，训练过程可参考附录3。

本节通过2个实例的研究来验证所述算法的有效性。实例1是在洗衣机运行的基础上，投入吹风机、电磁炉、电视机、热水壶。测量其事件检测效果和特征误差，并与当前常用的CUSUM、GLR算法进行对比。实例2是在洗衣机运行的基础上，投入13种不同特性的电器，重复算例1的试验。

4.2. 评价指标

事件检测可以看成一个二分类问题，即对每一时刻的检测结果只有两种可能：发生或未发生负荷事件。因此引入二分类算法性能评价中常用的混淆矩阵(Confusion Matrix)，将检测结果分成四类：真正类(TP，实际的负荷事件被检测出)、假正类(FP，未发生负荷事件却被误检为有发生)、假负类(FN，实际发生的负荷事件被漏检)和真负类(TN，实际未发生负荷事件，且与检测结果一致)。在进行有限次负荷投切操作的情况下，TN的值一定是远大于其他三类的。为了规避这种样本类别失衡的影响，选取的评估指标应不依赖于TN类的值。因此，以精确率(Precision)、召回率(Recall)和F_Score作为测试算例结果的评价指标，三种评价指标可分别按照式(9)、式(10)和式(11)计算求得。

$\text{Precision}=\frac{\left|TP\right|}{\left|TP\right|+\left|FP\right|}$ (9)

$\text{Recall}=\frac{\left|TP\right|}{\left|TP\right|+\left|FN\right|}$ (10)

$\text{F\_Score}=\frac{2}{\frac{1}{\text{Precision}}+\frac{1}{\text{Recall}}}$ (11)

如式(9)和式(10)所示，精确率表示所有被检测为发生的负荷事件中实际发生的事件的占比，其衡量事件检测方法能否检测准确的能力；召回率表示检测出的负荷事件占所有实际发生的事件的比例，其衡量事件检测方法能否检测全面的能力。如式(11)所示，F_Score是精确率和召回率的调和平均值，其能综合衡量事件检测算法在精确率和召回率这两个指标上的得分。

4.3. 实例1

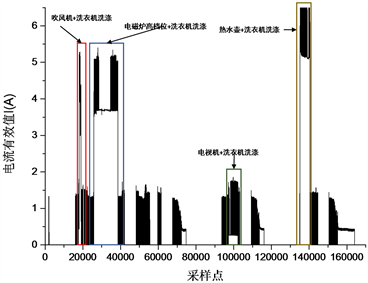
本算例采用用户在某个时间段的电流数据作为算例，如图4(a)所示，共包含167,585个采样点，采样

(a) (b)

Figure 4. RMS curve of mixed operation current of washing machine, hair dryer, induction cooker, TV set and hot kettle

图4. 洗衣机、吹风机、电磁炉、电视机、热水壶混合运行电流有效值曲线

频率为50 Hz，包括洗衣机、吹风机、电磁炉、电视机、热水壶5个电器，除洗衣机外共有10个负荷事件。为测试事件检测对特征提取的影响，分别对每次事件提取功率特征。表2为吹风机、电磁炉、电视机、热水壶单独运行时的特征。

如图4(b)所示，经过3.4节的第3步处理后，洗衣机运行所产生的周期性波形几乎都被删除，仅剩下洗衣机甩干2阶段的波形与其他电器运行数据。第3步处理过程见附录2。再进行3.4第4步处理，结果如表1所示。根据表1提取差量特征，结果如表3所示。

Table 1. Results of event detection

表1. 事件检测结果

Table 2. Operating power of hair dryer, induction cooker, TV set and hot kettle

表2. 吹风机、电磁炉、电视机、热水壶运行功率

Table 3. Comparison of feature extraction results

表3. 特征提取结果对比

由表1、表2可知，本文算法与CUSUM、GLR在事件的检测效果相似，但在电器特征提取的准确性上表现更优。由表3可知，基于本文算法提取的特征与电器单独运行时特征相近，而基于CUSUM与GLR算法所提取的特征与电器单独运行时特征存在较大的差距。通过分析发现：CUSUM和GLR所检测到的事件包含洗涤波形，如图5所示。CUSUM算法与GLR算法即使检测到该事件，特征提取会包含2个电器的特征叠加，导致负荷识别错误。而本文算法，是在剥离周期性波形的基础上进行事件检测，因此不存在特征叠加问题。因此，本文算法可保证特征提取以及负荷识别的准确性。由于删除了洗衣机波形，检测到的时间点与实际事件发生的时间点相差大约1 s，即一个波形的时间。

Figure 5. The current effective value curve of hair dryer and washing machine in mixed operation

图5. 吹风机与洗衣机混合运行的电流有效值曲线

4.4. 实例2

本算例以仿真实验室连续测量十次洗衣机运行的电流数据作为算例，如图6所示，共包含1,800,000个采样点，采样频率为50 Hz，包括洗衣机、吹风机、电磁炉、电视机、热水壶、电饭煲、电风扇、热水器、消毒柜、油烟机、定频空调、微波炉、电暖气、电烤箱14个电器，除洗衣机外共有73个负荷事件。事件检测结果如表4所示。

Figure 6. Current effective value curve

图6. 有效值曲线

Table 4. Results of event detection

表4. 事件检测结果

由表4可得，本文算法在精确率上与CUSUM算法相似，但在召回率和F_score上的表现更优(分别提高了6.85%和4.33%)。而与GLR算法相比，本文算法在三个指标上都有更优的表现(分别提高了4.74%、10.96%和7.91%)。基于上述分析，在含有洗衣机等周期性电器的家庭中，本文提出的基于CUSUM与shapeDTW混合事件检测算法具有比CUSUM与GLR更好的事件检测效果，更能保证特征提取的准确性和有效性。

5. 结论

事件检测是非侵入式负荷监测的基础环节，其准确性将影响整个负荷分解与识别的效果。针对洗衣机运行造成的多事件同时发生的问题，本文研究了混合事件检测方法。通过仿真实验数据验证对比表明：

1) 在洗衣机运行背景下，就对特征提取的影响而言，相比于CUSUM和GLR算法，混合事件检测算法可保证提取的差量特征的准确性，为后续的特征提取、负荷辨识等工作打下了基础。

2) 在洗衣机运行背景下，就检测效果而言，混合事件检测算法较CUSUM和GLR算法具有更高的精确率。因此更适用于用户非侵入式负荷监测的工程实际。

本文算法不仅适用于洗衣机，还适用于电磁炉、微波炉等其他含有周期性波形的设备的识别。同时还具备识别未知周期性设备和自适应建立周期性波形数据库的能力。综上，本文算法在提高检测能力的同时，可以保证特征提取的准确性，提高负荷识别准确率。

附录

1. 正文图

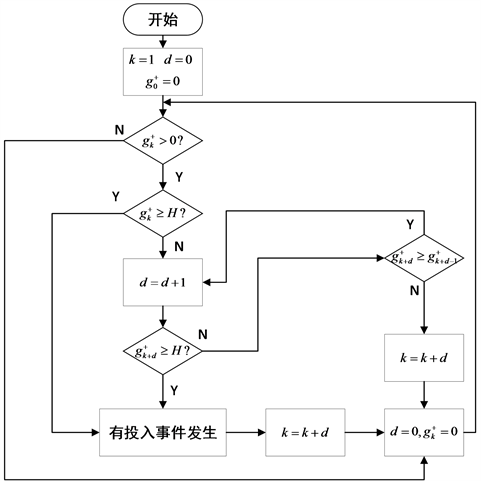
Figure A1. Sliding window bilateral CUSUM event detection algorithm flow

附图1. 滑动窗双边CUSUM事件检测算法流程

(a) DTW 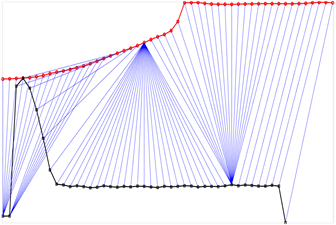(b) shapeDTW

Figure A2. Comparison of DTW and SHAPEDTW matching paths

附图2. DTW与shapeDTW匹配路径对比

2. 建立自适应波形数据库

1) 周期性波形数据库

波形数据库中一共6种波形，如附图3所示：① 洗衣机洗涤；② 洗衣机洗涤→脱水；③ 洗衣机甩干1阶段；④ 电磁炉文火挡位；⑤ 电饭煲保温挡位；⑥ 微波炉低档位。

(a) 洗衣机洗涤 (b) 洗衣机洗涤→脱水 (c) 洗衣机甩干1阶段 (d) 电磁炉文火挡位 (e) 电饭煲保温 (f) 微波炉低档位

Figure A3. Periodic waveform database

附图3. 周期性波形数据库

2) 检测周期性波形流程

① 通过CUSUM_1检测完整的启停波形，如附图4所示。

② 将检测到的波形进行shapeDTW匹配，以附图4波形为例，shapeDTW匹配结果如附表1所示。

③ 若出现连续3次波形匹配为同一个电器，则认为此时打开了该电器。

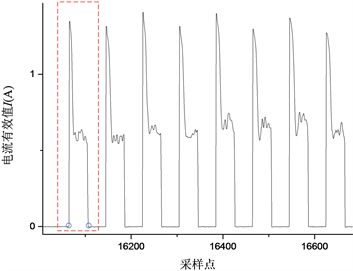
Figure A4. Start and stop waveform detection in washing machine

附图4. 洗衣机洗涤阶段启停波形检测

Table A1. Matching results of shapeDTW

附表1. shapeDTW匹配结果

由附表1可知，待匹配波形与洗衣机洗涤的DTW距离最小，即该波形属于洗衣机洗涤波形。

3. 阈值训练

1) H、h训练过程

考虑到本算例中，除洗衣机外，电器的事件发生间隔大多数在50个采样点以上，取CUSUM和GLR算法窗口长度为50。

如附图5所示，共包含150,000个采样点，采样频率为50 Hz，包括吹风机、电磁炉、电视机、热水壶、油烟机、消毒柜、热水器、电风扇、电饭煲9种电器。检测过程累积和如附图6所示。取 $H\in \left(0,4\right)$，间隔为0.5。取 $h\in \left(0,4\right)$，间隔为1。事件检测结果如附表2、附表3所示。

Figure A5. Current effective value curve

附图5. 电流有效值曲线

Figure A6. Test process accumulation and schematic diagram

附图6. 检测过程累计和示意图

Table A2. Event detection results of CUSUM

附表2. CUSUM事件检测结果

Table A3. Event detection results of GLR

附表3. GLR事件检测结果

附表2可得，H取3.5时，CUSUM检测效果最好。由附表3可得，h取3.5时，GLR检测效果最好。

2) T的训练过程

T的取值应至少满足：同类波形到聚类中心的DTW距离T_r小于T。如式(12)所示。

$\begin{array}{l}T=\max \left(T_r\right),r=1,2,3,4,5,6\\ T_r=\underset{j\in C_i}{\max }\left(\text{DTW}\left(z_j-m_i\right)\right)\end{array}$ (12)

其中C_i是第i类的所有样本。m_i是第i类的聚类中心。 $\text{DTW}\left(z_j-m_i\right)$ 表示第i类的样本z_j到该聚类中心的DTW距离。

Table A4. Tr distances for different waveforms

附表4. GLR事件检测结果

本文周期性波形数据库共有6种波形，T_r如附表4所示。因此T ≥ 184.25，取T = 185。