基于Tucker分解的频率和时延联合估计算法

Joint Frequency and Time-Delay Estimation Using Tucker Decomposition

摘要: 本文提出了一种基于Tucker分解的频率和时延联合估计算法。通过相邻阵元接收的正弦信号之间的时延特征构造信号张量，其频率和时延信息可利用张量Tucker分解之后的信号子空间通过ESPRIT算法求得。计算机仿真验证了所提算法的性能。

Abstract: In this paper, we develop an algorithm based on tucker decomposition method for estimating the differential delay of a sinusoid signal received at two separated sensors as well as the sinusoidal frequencies. Using tucker method, the reconstructed signal tensor is decomposed, the frequency and time delay estimates are obtained by ESPRIT from the signal subspace. Performance evaluation via computer simulations is included to demonstrate the effectiveness of the proposed algorithm.

1. 引言

频率和时延联合估计的应用包括丘脑皮质癫痫发作路径分析 [1]、频率–移位键控(FSK)调解 [2] 和说话人定位 [3] 等。本文研究了接收信号是正弦信号的频率和时延参数估计问题。

双阵元接收信号数据中蕴含了频率和时延信息，要从中进行参数估计，一般可以先估计其中的一个参数，再对另一个参数进行估计。目前，在正弦信号的频率估计和时延估计领域，有几种常见算法，包括PARAFAC方法(Parallel Factor Analysis) [4]、传统子空间方法 [5]、状态空间实现方法 [6] 和三线性交替最小二乘方法(Trilinear Alternating Least Square, TALS) [7] 等。文献 [4] 中提出了一种基于PARAFAC的频率和时延联合估计方法，该方法将数据矩阵重排，构造三个目标矩阵，利用交替最小二乘方法迭代求解，直到达到收敛条件。该方法多次迭代会影响算法速度。但该方法在样本数过大时，计算量会显著提升。文献 [5] 中提出了基于传统的子空间方法的时延和频率估计由数据矩阵的特征矢量与对应的特征值得到频率与时延信息。该方法需要进行两次矩阵的特征矢量分解，所以运算量较大，不利于实现。文献 [6] 中提出的基于状态空间的频率和时延联合估计算法，该算法通过构造状态空间模型，利用信号的协方差矩阵求得频率和时延信息。在采样数较大时，算法的精确度依赖于参数的取值。与传统方法相比，基于状态空间的时延估计结果具有闭式解，不需要搜索计算。文献 [7] 中提出了TALS方法，其基本思想是每一步更新一个矩阵，对余下的矩阵使用最小二乘(LS)来更新，直到算法收敛。由于TALS算法是基于迭代的最小二乘算法，所以会增加算法复杂度。本文以克拉美罗界(Cramér-Rao bound, CRLB)为算法的评价标准，克拉美罗界CRLB是信号的波达方向或者频率参数估计中一个作为算法性能指标的基准，是理想状态下算法所能达到的最优状态。当算法越靠近CRLB时，说明算法性能越好 [8]。现有的子空间方法拓展到多维信号一般是通过堆叠后利用矩阵来存储，显然这种方式构造不能准确的表达R-D固有数据的结构，而张量方法则可以更自然的对多维数据进行存储和操作。张量的Tucker分解最早由Tucker等人于1963年提出 [9]，随后又进一步的发展了这一理论，在1966年Tucker发表的一篇论文之后被学术界大量引用 [10]，是最早和最全面的关于张量Tucker分解方法概括的文章。Tucker分解有很多叫法，1986年，Kapteyn等学者发表的文章称这种分解方法为N-modePCA方法 [11]；DeLathauwer在2000年发表的文章中将这种分解称为高阶SVD分解 [12]。Tucker分解的实质，其实是PCA的高阶形式，将一个张量分解为核张量与各mode展开矩阵的乘积。本文提出了将张量Tucker分解和频率时延联合估计相结合的方法，利用张量来分析和处理多维数据并分离出信号子空间，为频率和时延联合估计提供了一种新的方法。同时，Tucker分解直接分离出信号子空间的奇异向量，利用ESPRIT算法一步求解就能估计出频率和时延参数，Tucker求解的过程中用到了快速算法Tucker3模型 [13]，处理方法简单明了，有效降低了算法的运算时间，提高了运算速度。仿真结果表明所提算法有良好的性能和较低的时间复杂度。

2. 问题描述及基本算法

正弦信号的频率估计和基于双阵元的时间延迟估计是信号处理中的热门研究主题，在最近的二十年中得到了较大的发展。对于单个正弦信号，用基于Fourier变换的方法可以获得精确的时延和频率估计 [14]。而对于多个正弦波的情形，一般的基于子空间方法和PARAFAC方法计算量较大，分辨率受其精度限制。所以本文提出一种张量Tucker分解的方法来估计频率和时延，有效的降低了算法的运算时间，并且有较好的性能。

不失一般性，基于双阵元正弦接收信号的模型为：

$\begin{array}{l}{r}_1\left(n\right)=s\left(n\right)+q_1\left(n\right)\\ r_2\left(n\right)=s\left(n-D\right)+q_2\left(n\right),n=0,1,\cdots ,N-1\end{array}$ (1)

其中， $s\left(n\right)={\displaystyle {\sum }_{m=1}^P{\alpha }_m}\exp \left(j{\omega }_{m}n\right)$ 由P个复正弦信号组成。假设P先验已知，信号中第m个分量的复振幅和频率分别用 ${\alpha }_m$ 和 ${\omega }_m$ 表示。 $s\left(n-D\right)$ 为相邻含时延阵元的接收信号，D表示时延，N为采样数。接收信号数据中含有的零均值复高斯白噪声用 $q_1\left(n\right)$ 和 $q_2\left(n\right)$ 表示，它们互不相关且方差为 ${\sigma }_q^2$。

将两个相邻阵元的接收信号重排为 $x\left(n\right)$ ：

$x\left(n\right)={\left[r_1\left(n\right),r_1\left(n+1\right),\cdots ,r_1\left(n+M-1\right),r_2\left(n\right),r_2\left(n+1\right),\cdots ,r_2\left(n+M-1\right)\right]}^{\text{T}},n=0,1,\cdots ,K-1$ (2)

其中， $K=N-M+1$，“T”表示转置操作。K在 $P+1$ 和 $N-P+1$ 之间取值，这样当n变化时， $x\left(n\right)$ 的秩都小于P，M为矢量长度且远大于P。公式(2)中的状态空间模型为：

$s\left(n+1\right)=\Phi s(\; n\; )$

$x\left(n\right)=Bs\left(n\right)+q\left(n\right)$ (3)

其中， $s\left(n\right)={\left[{\alpha }_1{\text{e}}^{j{\omega }_{1}n},{\alpha }_2{\text{e}}^{j{\omega }_{2}n},\cdots ,{\alpha }_p{\text{e}}^{j{\omega }_{p}n}\right]}^{\text{T}}$， $\Phi =\text{diag}\left({\text{e}}^{j{\omega }_1}{\text{,e}}^{j{\omega }_2},\cdots {\text{,e}}^{j{\omega }_p}\right)$， $\text{B}={\left[{\text{A}}^{\text{T}}{\left(\text{A}\Delta \right)}^{\text{T}}\right]}^{\text{T}}$

$\text{A}=[\begin{array}{c}\text{1}\\ {\text{e}}^{j{\omega }_1}\\ ⋮\\ {\text{e}}^{j{\omega }_1\left(M-1\right)}\end{array}\begin{array}{c}\text{1}\\ \begin{array}{l}{\text{e}}^{j{\omega }_2}\\ ⋮\end{array}\\ {\text{e}}^{j{\omega }_2\left(M-1\right)}\end{array}\begin{array}{c}\cdots \\ \cdots \\ \ddots \\ \cdots \end{array}\begin{array}{c}\text{1}\\ \begin{array}{l}{\text{e}}^{j{\omega }_p}\\ ⋮\end{array}\\ {\text{e}}^{j{\omega }_p\left(M-1\right)}\end{array}]$

$\Delta =\text{diag}\left({\text{e}}^{-jD{\omega }_1},{\text{e}}^{-jD{\omega }_2},\cdots ,{\text{e}}^{-jD{\omega }_P}\right)$

$q\left(n\right)={\left[q_1\left(n\right),q_1\left(n+1\right),\cdots ,q_1\left(n+M-1\right),q_2\left(n\right),q_2\left(n+1\right),\cdots ,q_2\left(n+M-1\right)\right]}^{\text{T}}$

$L\ge 2$ 是一给定的正整数，定义向量 $X_l=\left[x\left(1+l\right),\cdots ,x\left(K-L+l+1\right)\right]$，通过状态空间模型有：

$X_l=B{\Phi }_{l}S+Q_l,l=0,1,\cdots ,L-1$ (4)

其中， ${\Phi }_l=\text{diag}\left({\text{e}}^{jl{\omega }_1},{\text{e}}^{jl{\omega }_2},\cdots ,{\text{e}}^{jl{w}_P}\right)$， $S=\left[s\left(1\right),\cdots ,s\left(K-L+1\right)\right]$， $Q_l=\left[q\left(1+l\right),\cdots ,q\left(K-L+l+1\right)\right]$。

给定 $i\left(i=1,2,\cdots ,K-L+1\right)$，将(4)式中 $X_l$ 通过矩阵重排，构造成三维切片形式。在不考虑噪声的情况下，可以构成含频率和时延信息的三维流形 [12]：

$X\left(i,:,:\right)=x_n\left(:,i:\left(i+L-1\right)\right),i=1,2,\cdots ,K-L+1$ (5)

其中，公式(2)中的 $x\left(n\right)$ 用 $x_n$ 表示。

将(5)式的信号三维流形X张量化，构造张量 $\mathcal{X}\in {ℂ}^{(K-L+1)\times 2M\times L}$，可以将其通过Tucker分解为：

$\mathcal{X}=\mathcal{G}\times {}_1\text{U}{}_1\times {}_{\text{2}}\text{U}{}_{\text{2}}\times {}_{\text{3}}\text{U}{}_3$ (6)

其中， $\mathcal{G}\in {ℂ}^{(K-L+1)\times 2M\times L}$ 称为张量核，并满足文献 [15] 中所述的全正交条件。 ${\text{U}}_1\in {ℂ}^{(K-L+1)\times (K-L+1)}$， ${\text{U}}_2\in {ℂ}^{2M\times 2M}$， ${\text{U}}_3\in {ℂ}^{L\times L}$ 为酉矩阵，即满足 ${\text{U}}_r{\text{U}}_r^H={\text{I}}_r,r=1,2,3$， ${\text{I}}_r$ 是规模与 ${\text{U}}_r$ 相同的单位矩阵。通过Tucker分解，张量 $\mathcal{X}$ 的r-mode奇异向量 ${\text{U}}_r,r=1,2,3$ 中含有P个正弦信号的频率信息和相邻阵元的时延信息。

由式(6)可知，张量核 $\mathcal{G}$ 的秩为P [15]，则有

$\tilde{\mathcal{X}}={\tilde{\mathcal{G}}}^{[P]}\times {}_1\tilde{U}{}_1^{[P]}\times {}_{\text{2}}\tilde{U}{}_2^{[P]}\times {}_{\text{3}}\tilde{U}{}_3^{[P]}$ (7)

其中， ${\tilde{\mathcal{G}}}^{[P]}\in {ℂ}^{P\times P\times P}$， ${\tilde{U}}_{\text{1}}^{[P]}\in {ℂ}^{(K-L+1)\times }{}^P$， ${\tilde{U}}_2^{[P]}\in {ℂ}^{2M\times }{}^P$， ${\tilde{U}}_3^{[P]}\in {ℂ}^{L\times }{}^P$， ${\tilde{U}}_r^{[P]}$ 是 ${\text{U}}_r$ 的前P个列向量。由于矩阵重排后的频率信息和时延信息包含在 ${\tilde{U}}_1^{[P]}$ 和 ${\tilde{U}}_2^{[P]}$ 中，可以利用对应的结构，找到信号子空间和噪声子空间。因此，可以先利用对应的 ${\tilde{U}}_1^{[P]}$ 的结构和ESPRIT方法 [16]，构造旋转不变矩阵 $\Phi$，其估计值用 $\tilde{\Phi }$ 表示：

$\tilde{\Phi }={\left[{\tilde{U}}_1^{[P]}\left(1:M-1\right),:\right]}^{\gamma }{\tilde{U}}_1^{[P]}\left(P:M,:\right)$ (8)

符号“ $\gamma$ ”表示伪逆操作，对 $\tilde{\Phi }$ 进行特征值分解：

$\tilde{\Phi }=V_s{\Lambda }_s{V}_s^H$ (9)

其中， $V_s\in {ℂ}^{P\times }{}^P$ 的列向量张成 $\tilde{\Phi }$ 的信号子空间，而 ${\Lambda }_s\in {ℂ}^{P\times }{}^P$ 的对角线元素为 $\tilde{\Phi }$ 的特征值。而特征值的对角元素就是对应的频率参数。接着对特征值求相位值，就可以估计出信号的频率信息。频率估计值可以求得为：

${\tilde{\omega }}_m=\angle {\Lambda }_s\left(m,m\right),m=1,2,\cdots ,P$ (10)

符号“ $\angle$ ”表示求相位角操作。因为Tucker分解分离出的 ${\tilde{U}}_2^{[P]}$ 中包含时延信息，所以利用 ${\tilde{U}}_2^{[P]}$ 的结构来估计 $\Delta$，首先对其求伪逆，值用 $\tilde{\Delta }$ 表示：

$\tilde{\Delta }={\left[{\tilde{U}}_2^{[P]}\left(1:M,:\right)\right]}^{\gamma }{\tilde{U}}_2^{[P]}\left(M+1:2M,:\right)$ (11)

最后，对于时延 $\tilde{D}$，其值可以用频率的估计值和 $\tilde{\Delta }$ 对角元素的加权平均的方法获得：

$\hat{D}=\frac{{\displaystyle {\sum }_{m=1}^P\angle \tilde{\Delta }\left(m,m\right)}}{-{\displaystyle {\sum }_{m=1}^P{\hat{\omega }}_m}}$ (12)

3. 仿真结果

在计算机仿真中，实验的对比算法选择为目前常见的且有代表性的PARAFAC算法、传统子空间算法(仿真图中的Subspace)和TALS算法。其中，性能指标以克拉美罗界为衡量标准(理想状态下，算法能达到的最好效果，即仿真图中的CRLB)。正弦信号 $s\left(n\right)$ 设置为 $s\left(n\right)={\alpha }_1{\text{e}}^{j{\omega }_{1}n}+{\alpha }_2{\text{e}}^{j{\omega }_{2}n}$， ${\alpha }_1=1/\sqrt{2}$， ${\alpha }_2=1/\sqrt{2}$， ${\omega }_1=0.2\pi \text{rad}/\text{s}$， ${\omega }_2=0.4\pi \text{rad}/\text{s}$。采样次数为 $N=100$， $M=25$， $L=\text{4}$。采样间隔为1s且时延 $D=1.7\text{s}$。所有的仿真图是在200次独立实验下取平均的结果。图1~3分别给出了两个分量的频率估计和时延估计的均方误差随信噪比变化的对比图。

Figure 1. MSE versus SNR for Frequency ${\omega }_1$

图1. 频率分量 ${\omega }_1$ 的均方误差和SNR图

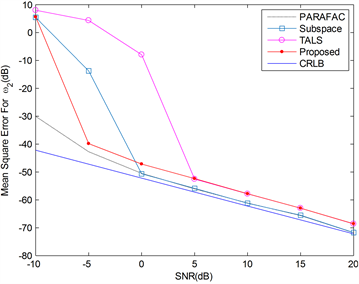
Figure 2. MSE versus SNR for Frequency ${\omega }_2$

图2. 频率分量 ${\omega }_2$ 的均方误差和SNR图

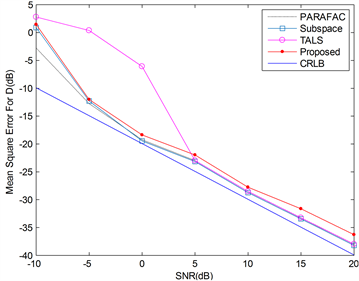
Figure 3. MSE versus SNR for Frequency ${\omega }_3$

图3. 频率分量 ${\omega }_3$ 的均方误差和SNR图

从图1、图2及图3来看，基于PFA方法和基于子空间的方法更接近于CRLB下界，所提算法的第一个频率分量的算法估计性能优于TALS，且接近于子空间方法性能。在信噪比小于−5 dB时，所提算法的第二个个频率分量的算法估计性能优于子空间方法和TALS方法。图3在信噪比为−10 dB到−5 dB时，所提算法的时间延迟估计D远高于TALS方法，性能与子空间方法相似(见图3)。

图4给出了频率 ${\omega }_1$ 以 $0.01\pi$ 的步长从 $0\pi$ 变化至 $0.3\pi$ 的频率间隔变化图，实验在SNR = 5下进行，其余参数不变(见图4)。

从图4来看，所提算法在 $0\pi$ 到 $0.06\pi$ 的高分辨率下，性能优于PFA方法和TALS方法，随着频率间隔逐渐增大，所提算法的性能则不如PFA方法和TALS方法，而基于子空间方法分辨率最高。

图5给出了算法的时间复杂度，采样数N从100以步长为5增加到145。在计算量需求方面，PARAFAC方法在迭代次数为 $\lambda$ 次的算法复杂度为 $o\left(3\lambda \left(P^3+2PLM\left(N-M-L+2\right)\right)\right)$ [17]，由大量仿真实验表明，当M和L越大，性能越高，但同时计算量也越大。子空间方法的算法复杂度为 $o\left({\left(2PL\right)}^2\left(N-M+1\right)+8P^3{L}^3\right)$ [6]，TALS的算法复杂度为 $o\left(2\left(N-M+1\right)MLPr\right)$ [18]，本文所提算法的复杂度为 $o\left(2\left(N-M+1\right)ML\right)$ [15]，其计算代价最低，而且随着采样数的增加，复杂度增长最慢。

Figure 4. Frequency resolution

图4. 频率分辨率图

Figure 5. Computational time compared

图5. 运算复杂度比较图

从图5来看，所提算法时间复杂度最低。随着采样数的增加，基于PFA算法的时间复杂度增长要快于其他算法，TALS方法次之，子空间算法时间复杂度增长较慢，而在同等采样数下，所提算法的时间复杂度增长最慢(见图5)。

4. 结论

本文提出了一种利用张量Tucker分解的频率和时延联合估计算法。所提算法通过构造信号张量，利用张量Tucker分解，分离出信号的r-mode奇异向量，再通过ESPRIT算法估计出频率和时延参数。Tucker分解利用了Tucekr3模型 [13] 使其算法速度极大提升，同时在较低信噪比下，也能达到很好的性能。仿真结果表明所提算法在时间复杂度上要优于TALS方法、PARAFAC方法和子空间方法。参数估计过程中，参数兼并是一个十分重要的问题，本文所研究的算法无法较好的处理参数兼并问题。将来的工作重点之一是能研究有效解决参数兼并的快速算法。

基金项目

国家自然科学基金(No.61771353)资助课题。