一种改进的MQ拟插值方法及其性质

A New Quasi Interpolation Scheme for MQ Radial Basis Function

摘要: 本文基于Wu-Schaback拟插值算子L_DF(X)构造了一种新的MQ径向拟插值算子，该算子增加了在两端点处的一阶导数的线性组合项，并结合三点微分公式替代其两端点处的导数值，提高了该算子的收敛阶。通过理论分析得出该算子的线性多项式具有再生性、二阶保形性和较高的收敛阶等优点。最后，通过数值实验比较了该拟插值格式与Wu-Schaback和Feng-Li的拟插值格式的近似能力，数值计算结果证实了理论分析的正确性，验证了该算子对数值求解中的有效性。

Abstract: Based on Wu-schaback’s Quasi interpolation operator, a new MQ radial quasi interpolation operator is proposed. The operator has the advantages of linear polynomial regeneration, shape-preserving property of order 2 and high convergence rate, and does not need the derivative of the function at the end point. Through theoretical analysis, it is concluded that the linear polynomial of the operator has the advantages of reproducibility, second-order shape preservation and higher convergence order. Finally, the approximation ability of the proposed scheme is compared with Wu-scha- back’s and Feng Li’s quasi interpolation scheme by numerical experiments. The numerical results confirm the conclusion of the theoretical analysis and the effectiveness of the operator.

1. 引言

插值是函数逼近的一种经典而又十分重要的方法。随着径向基函数的发展，许多的研究者利用径向基函数构造插值函数去解决问题，并取得了不错的效果。Powell [1] 将MQ径向基函数转移到一维空间的离散数据上，构造了拟插值函数 $Lf\left(x\right)$，使 $Lf\left(x\right)$ 满足了线性多项式的再生性。然后，Beatson和Powell [2] 通过将MQ径向基函数转移至有限分散数据上，构造了拟插值算子 $L_{C}f\left(x\right)$，该算子满足线性多项式的再生性。然而，要求算子 $L_{C}f\left(x\right)$ 在 $f\left(x\right)$ 端点处的导数值，这在实际应用中很复杂。因此，Wu和Schaback [3] 对 $L_{C}f\left(x\right)$ 进行了适当的修改，构造了拟插值算子 $L_{D}f\left(x\right)$，该算子不必求得 $f\left(x\right)$ 在端点处的导数，也满足线性多项式的再生性质。但是，他们发现当 $c=O\left(h\right)$ 时，算子 $L_{D}f\left(x\right)$ 的误差不是 $O\left(h^2\right)$，而是 $O\left(h^2\left|\ln h\right|\right)$，其中h是相邻节点之间的最大距离。Leevan和Ling [4] 基于文献 [3] 提出了一种MQ径向基函数的多级单变量拟插值方案，并证明了该方案在当 $c=O\left(h\right)$ 时，收敛速率为 $O\left(h^{2.5}\left|\ln h\right|\right)$。而Zhang和Wu [5] 通过三次MQ-B样条原理，构造了四种保形性的拟插值算子，然而这些算子不能满足多项式的再现性，并且要求 $f\left(x\right)$ 在端点处的导数。Feng和Li [6] 构造了一个保形拟插值算子，该算子满足三次MQ径向基函数对离散数据的二次多项式再生性，并证明了它的逼近速率最大为 $O\left(h^3\right)$。Walddron [7] 在m次多项式的拟插值算子的基础上，构造了再现 $\left(m+r\right)$ 次多项式的拟插值算子( $r$ 为非负整数)。但是，它涉及到 $f\left(x\right)$ 在每一个节点的导数，并且要求被逼近函数额外的 $r$ 阶光滑。Chen et al. [8] 利用Hermite插值多项式设计了一种新的的MQ拟插值算子，该具有线性再生和保持单调性。Wang et al. [9] 提出了一种改进的单变量MQ拟插值算子，并在一定的假设下给出了收敛速度。在文献 [10] - [15] 中，也可以发现更多关于MQ拟插值的应用。

本文的结构如下：首先，在第2节，我们介绍了一些必要的定义及拟插值函数的相关性质。接着，我们通过修正满足线性多项式再生性质的拟插值算子 $L_{D}f\left(x\right)$ 构造了一种新的MQ拟插值算子。在第3节中，详细讨论了该算子二阶保形性质，收敛性及其收敛阶。在第4节中，我们通过数值实验比较了Wu-Schaback和Feng-Li与该拟插值算子拟插值格式的逼近能力，并通过实例验证了该拟插值算子的收敛速度。最后，在第5节，我们给出了一些结论和未来的工作安排。

2. MQ径向拟插值格式的构造

2.1. 预备知识

本节首先给出一些必要的定义和已知的结论。

定义2.1 [3] 给定一组散乱的数据 $a=x_0<x_1<\cdots <x_n=b$，函数 $f\left(x\right):C\left[a,b\right]\to R$ 的拟插值算子 $Lf\left(x\right)$ 定义为：

$Lf\left(x\right)={\displaystyle \underset{j=0}{\overset{n}{\sum }}f\left(x_j\right){\alpha }_j\left(x\right),}x\in \left[a,b\right]$

其中 ${\alpha }_j\left(x\right)$ 为拟插值基函数。

定义2.2 [3] 假设由数据点 ${\left\{x_j,f\left(x_j\right)\right\}}_{j=1}^n$ 构造而成的 $Lf\left(x\right)$ 是函数 $f\left(x\right)$ 的近似，如果数据点 ${\left\{x_j,f\left(x_j\right)\right\}}_{j=1}^n$ 的 $k$ 阶导函数是非负的，并且 $Lf\left(x\right)$ 的 $k$ 阶导函数也是非负的，那么 $Lf\left(x\right)$ 则具有 $k$ 阶的保形性。特别的，一阶保形性称为保单调性，二阶的保形性称为保凸性。

下面，我们介绍已知的拟插值算子 $L_{D}f\left(x\right)$ 和 $L_{s}f\left(x\right)$。首先，对于给定的分散数据 $a=x_0<x_1<\cdots <x_n=b$，Wu和Schaback [3] 基于基函数 ${\varphi }_j\left(x\right)={\left({\left(x-x_j\right)}^2+c^2\right)}^{1/2}$ 构造了拟插值算子 $L_{D}f\left(x\right)$。

$L_{D}f\left(x\right)=f\left(x_0\right){\alpha }_0\left(x\right)+f\left(x_1\right){\alpha }_1\left(x\right)+{\displaystyle \underset{j=2}{\overset{n-2}{\sum }}f\left(x_j\right){\alpha }_j\left(x\right)}+f\left(x_{n-1}\right){\alpha }_{n-1}\left(x\right)+f\left(x_n\right){\alpha }_n(\; x\; )$

此时

${\alpha }_0\left(x\right)=\frac{1}{2}+\frac{{\varphi }_1\left(x\right)-\left(x-x_0\right)}{2\left(x_1-x_0\right)}$

${\alpha }_1\left(x\right)=\frac{{\varphi }_2\left(x\right)-{\varphi }_1\left(x\right)}{2\left(x_1-x_0\right)}-\frac{{\varphi }_1\left(x\right)-\left(x-x_0\right)}{2\left(x_1-x_0\right)}$

${\alpha }_1\left(x\right)=\frac{{\varphi }_{j+1}\left(x\right)-{\varphi }_j\left(x\right)}{2\left(x_{j+1}-x_j\right)}-\frac{{\varphi }_j\left(x\right)-{\varphi }_{j-1}\left(x\right)}{2\left(x_j-x_{j-1}\right)}$

${\alpha }_{n-1}\left(x\right)=\frac{\left(x_n-x\right)-{\varphi }_{n-1}\left(x\right)}{2\left(x_n-x_{n-1}\right)}-\frac{{\varphi }_{n-1}\left(x\right)-{\varphi }_{n-2}\left(x\right)}{2\left(x_{n-1}-x_{n-2}\right)}$

${\alpha }_n\left(x\right)=\frac{1}{2}+\frac{{\varphi }_{n-1}\left(x\right)-\left(x_n-x\right)}{2\left(x_n-x_{n-1}\right)}$

2.2. MQ拟插值算子的构造

在满足线性多项式再生的算子 $L_{D}f\left(x\right)$ 的基础上，对 $L_{D}f\left(x\right)$ 进行改进，并其后添加一阶导数的线性组合项，构造拟插值算子 $L_{1}f\left(x\right)$。针对实际问题中两端导数值不易求出的问题，利用三点微分公式代替一阶导数值，得到了新的MQ拟插值算子 $L_{2}f\left(x\right)$。具体形式如下：

$L_{1}f\left(x\right)=L_{D}f\left(x\right)+f^{\prime }\left(x_0\right){\lambda }_0\left(x\right)+f^{\prime }\left(x_n\right){\lambda }_n\left(x\right)x\in \left[a,b\right]$ (3.1)

$L_{2}f\left(x\right)=L_{D}f\left(x\right)+D_1\left(x_0\right){\lambda }_0\left(x\right)+D_2\left(x_n\right){\lambda }_n\left(x\right)x\in \left[a,b\right]$ (3.2)

此时

${\lambda }_0\left(x\right)=\frac{1}{2}\left(x-x_0\right)-\frac{1}{2}{\varphi }_0(\; x\; )$

${\lambda }_n\left(x\right)=\frac{1}{2}{\varphi }_n\left(x\right)-\frac{1}{2}\left(x_n-x\right)$

$D_1\left(x_0\right)\approx f^{\prime }\left(x_0\right)=\frac{1}{2h}\left[-3f\left(x_0\right)+4f\left(x_1\right)\right]-\frac{1}{2h}f(\; x\; 2\; )$

$D_2\left(x_n\right)\approx f^{\prime }\left(x_n\right)=\frac{1}{2h}\left[f\left(x_{n-2}\right)-4f\left(x_{n-1}\right)\right]+\frac{\text{3}}{\text{2}h}f(\; x\; n\; )$

3. MQ拟插值算子的相关性质

定理3.1 MQ拟插值算子 $L_{1}f\left(x\right)$ 和 $L_{2}f\left(x\right)$ 满足线性多项式再生性质。

证明：

$\begin{array}{c}{L}_{1}f\left(x\right)=L_{D}f\left(x\right)+f^{\prime }\left(x_0\right){\lambda }_0\left(x\right)+f^{\prime }\left(x_n\right){\lambda }_n\left(x\right)\\ =f\left(x_0\right)\left(\frac{1}{2}+\frac{{\varphi }_1\left(x\right)-x+x_0}{2\left(x_1-x_0\right)}\right)+f\left(x_1\right)\frac{{\varphi }_2\left(x\right)-{\varphi }_1\left(x\right)}{2\left(x_2-x_1\right)}-f\left(x_1\right)\frac{{\varphi }_1\left(x\right)-x+x_0}{2\left(x_1-x_0\right)}\\ +{\displaystyle \underset{j=2}{\overset{n-2}{\sum }}f\left(x_j\right)}\left(\frac{{\varphi }_{j+1}\left(x\right)-{\varphi }_j\left(x\right)}{2\left(x_{j+1}-x_j\right)}-\frac{{\varphi }_j\left(x\right)-{\varphi }_{j-1}\left(x\right)}{2\left(x_j-x_{j-1}\right)}\right)\\ +f\left(x_{n-1}\right)\left(\frac{x_n-x-{\varphi }_{n-1}\left(x\right)}{2\left(x_n-x_{n-1}\right)}-\frac{{\varphi }_{n-1}\left(x\right)-{\varphi }_{n-2}\left(x\right)}{2\left(x_{n-1}-x_{n-2}\right)}\right)\\ +f\left(x_n\right)\left(\frac{1}{2}+\frac{{\varphi }_{n-1}\left(x\right)+x-x_n}{2\left(x_n-x_{n-1}\right)}\right)+f^{\prime }\left(x_0\right)\frac{x-x_0-{\varphi }_0\left(x\right)}{2}\end{array}$

如果 $f\left(x\right)=x$，那么

$\begin{array}{c}{L}_{1}f\left(x\right)=L_{D}f\left(x\right)+f^{\prime }\left(x_0\right){\lambda }_0\left(x\right)+f^{\prime }\left(x_n\right){\lambda }_n\left(x\right)\\ =x_0\left(\frac{1}{2}+\frac{{\varphi }_1\left(x\right)-x+x_0}{2\left(x_1-x_0\right)}\right)+x_1\frac{{\varphi }_2\left(x\right)-{\phi }_1\left(x\right)}{2\left(x_2-x_1\right)}-x_1\frac{{\varphi }_1\left(x\right)-x+x_0}{2\left(x_1-x_0\right)}\\ +{\displaystyle \underset{j=2}{\overset{n-2}{\sum }}{x}_j}\left(\frac{{\varphi }_{j+1}\left(x\right)-{\varphi }_j\left(x\right)}{2\left(x_{j+1}-x_j\right)}-\frac{{\varphi }_j\left(x\right)-{\varphi }_{j-1}\left(x\right)}{2\left(x_j-x_{j-1}\right)}\right)\\ +x_{n-1}\left(\frac{x_n-x-{\varphi }_{n-1}\left(x\right)}{2\left(x_n-x_{n-1}\right)}-\frac{{\varphi }_{n-1}\left(x\right)-{\varphi }_{n-2}\left(x\right)}{2\left(x_{n-1}-x_{n-2}\right)}\right)\\ +x_n\left(\frac{1}{2}+\frac{{\varphi }_{n-1}\left(x\right)+x-x_n}{2\left(x_n-x_{n-1}\right)}\right)\\ =x\end{array}$

对于算子 $L_{2}f\left(x\right)$，同理也可证明。

定理3.2 如果数据序列 ${\left\{f\left(x_j\right)\right\}}_{j=0}^n$ 中的数据是从单调函数 $f\left(x\right)\left(x\in C\left[x_0,x_n\right]\right)$ 中取得，则拟插值算子 $L_{1}f\left(x\right)$ 和 $L_{2}f\left(x\right)$ 也是单调函数。

证明： $L_{1}f\left(x\right)$ 的一阶导数为

$\begin{array}{c}{L}_1{f}^{\prime }\left(x\right)=\left(\frac{{{\varphi }^{\prime }}_1\left(x\right)-1}{2\left(x_1-x_0\right)}\right)f\left(x_0\right)-\left(-\frac{{{\varphi }^{\prime }}_1\left(x\right)-1}{2\left(x_1-x_0\right)}\right)f\left(x_1\right)+\left(\frac{{{\varphi }^{\prime }}_2\left(x\right)-{{\varphi }^{\prime }}_1\left(x\right)}{2\left(x_2-x_1\right)}\right)f\left(x_1\right)\\ +{\displaystyle \underset{j=2}{\overset{n-2}{\sum }}f\left(x_j\right)}\left(\frac{{{\varphi }^{\prime }}_{j+1}\left(x\right)-{{\varphi }^{\prime }}_j\left(x\right)}{2\left(x_{j+1}-x_j\right)}-\frac{{{\varphi }^{\prime }}_j\left(x\right)-{{\varphi }^{\prime }}_{j-1}\left(x\right)}{2\left(x_j-x_{j-1}\right)}\right)\\ -f\left(x_{n-1}\right)\left(\frac{{{\varphi }^{\prime }}_{n-1}\left(x\right)-1}{2\left(x_n-x_{n-1}\right)}+\frac{{{\varphi }^{\prime }}_{n-1}\left(x\right)-{{\varphi }^{\prime }}_{n-2}\left(x\right)}{2\left(x_{n-1}-x_{n-2}\right)}\right)\end{array}$

$\begin{array}{c}+f\left(x_n\right)\frac{{{\varphi }^{\prime }}_{n-1}\left(x\right)+1}{2\left(x_n-x_{n-1}\right)}+f^{\prime }\left(x_0\right)\frac{1-{{\varphi }^{\prime }}_0\left(x\right)}{2}+f^{\prime }\left(x_n\right)\frac{{{\varphi }^{\prime }}_n\left(x\right)+1}{2}\\ =\frac{\text{1}}{\text{2}}{\displaystyle \underset{j=1}{\overset{n-2}{\sum }}{f}^{\prime }\left(x_j\right)\left({{\varphi }^{\prime }}_j\left(x\right)-{{\varphi }^{\prime }}_{j+1}\left(x\right)\right)}+\frac{\text{1}}{\text{2}}{f}^{\prime }\left(x_0\right)\left(1-{{\varphi }^{\prime }}_1\left(x\right)\right)+f^{\prime }\left(x_0\right)\frac{1-{{\varphi }^{\prime }}_0\left(x\right)}{2}\\ +\frac{\text{1}}{\text{2}}{f}^{\prime }\left(x_{n-1}\right)\left({{\varphi }^{\prime }}_{n-1}\left(x\right)+1\right)+\frac{1}{2}{f^{\prime }}_n\left(x_n\right)\frac{{{\varphi }^{\prime }}_n\left(x\right)+1}{2}\end{array}$

对任意的 $x\in R,-1\le {{\varphi }^{\prime }}_{j+1}\left(x\right)\le {{\varphi }^{\prime }}_j\left(x\right)\le 1$ 因此，当 $f^{\prime }\left(x\right)>0,L_1{f}^{\prime }\left(x\right)>0$ ； $f^{\prime }\left(x\right)<0$ ； $L_1{f}^{\prime }\left(x\right)<0$。

另外，根据算子 $L_{2}f\left(x\right)$， $L_{2}f\left(x\right)$ 的一阶导数可计算为

$\begin{array}{c}{L}_2{f}^{\prime }\left(x\right)=\frac{\text{1}}{\text{2}}{\displaystyle \underset{j=1}{\overset{n-2}{\sum }}{f}^{\prime }\left(x_j\right)\left({{\varphi }^{\prime }}_j\left(x\right)-{{\varphi }^{\prime }}_{j+1}\left(x\right)\right)}+\frac{\text{1}}{\text{2}}{D}_1\left(x_0\right)\left(1-{{\varphi }^{\prime }}_1\left(x\right)\right)+\frac{\text{1}}{\text{2}}{f}^{\prime }\left(x_{n-1}\right)\left(1+{{\varphi }^{\prime }}_{n-1}\left(x\right)\right)\\ +\frac{1}{2}{D}_1\left(x_0\right)\left(\text{1}-{{\varphi }^{\prime }}_0\left(x\right)\right)+\frac{1}{2}{D}_2\left(x_n\right)(1+{{\varphi }^{\prime }}_n(\; x\; ))\end{array}$

从上面的公式可以看出，当 $f^{\prime }\left(x\right)>0,L_{\text{2}}{f}^{\prime }\left(x\right)>0$， $f^{\prime }\left(x\right)<0,L_{\text{2}}{f}^{\prime }\left(x\right)<0$。完成证明。

定理3.3 若 $\left[f^{\prime }\left(x_n\right){{\varphi }^{″}}_n(x)-f^{\prime }\left(x_0\right){\varphi }^{″}\left(x\right)\right]\ge 0$，则拟插值算子 $L_{1}f\left(x\right)$ 为严格二阶保形；若 $\left[D_2\left(x_n\right){{\varphi }^{″}}_n\left(x\right)-D_1\left(x_0\right){\varphi }^{″}\left(x\right)\right]\ge 0$，则拟插值算子 $L_{2}f\left(x\right)$ 是严格二阶保形。

证明： $L_{1}f\left(x\right)$ 的二阶导数

$\begin{array}{c}{L^{″}}_{1}f\left(x\right)=\frac{1}{2}{\displaystyle \underset{j=1}{\overset{n-1}{\sum }}{{\varphi }^{″}}_j\left(x\right)\left(f^{\prime }\left(x_j\right)-f^{\prime }\left(x_{j-1}\right)\right)}-\frac{\text{1}}{\text{2}}\left(f^{\prime }\left(x_0\right){{\varphi }^{\prime }}_0\left(x\right)+f^{\prime }\left(x_n\right){{\varphi }^{\prime }}_n\left(x\right)\right)\\ =\frac{1}{2}{\displaystyle \underset{j=1}{\overset{n-1}{\sum }}{{\varphi }^{″}}_j\left(x\right)\left(x_j-x_{j-1}\right)f^{″}\left(x\right)}-\frac{\text{1}}{\text{2}}{f}^{\prime }\left(x_0\right){{\varphi }^{″}}_0\left(x\right)+\frac{\text{1}}{\text{2}}{f}^{\prime }\left(x_n\right){{\varphi }^{\prime }}_n(\; x\; )\end{array}$

此时，

${{\varphi }^{″}}_j\left(x\right)=\frac{c^2}{{\left[c^2+{\left(x-x_j\right)}^2\right]}^{\frac{3}{2}}}\ge 0$

因此，当 $\left[f^{\prime }\left(x_n\right){{\varphi }^{″}}_n\left(x\right)-f^{\prime }\left(x_0\right){\varphi }^{″}\left(x\right)\right]\ge 0$，我们可以得到 $L_1{f}^{″}\left(x\right)\ge 0$。最后，我们证明了拟插值算子 $L_{1}f\left(x\right)$ 具有二阶保形性。

根据算子 $L_{2}f\left(x\right)$ 的二阶导数

$\begin{array}{c}{L^{″}}_{2}f\left(x\right)=\frac{1}{2}{\displaystyle \underset{j=1}{\overset{n-1}{\sum }}{{\varphi }^{″}}_j(x)\left(f^{\prime }\left(x_j\right)-f^{\prime }\left(x_{j-1}\right)\right)}-\frac{\text{1}}{\text{2}}\left(D_1\left(x_0\right){{\varphi }^{\prime }}_{\text{0}}\left(x\right)+D_2\left(x_n\right){{\varphi }^{″}}_n\left(x\right)\right)\\ =\frac{\text{1}}{\text{2}}{\displaystyle \underset{j=1}{\overset{n-1}{\sum }}{{\varphi }^{″}}_j\left(x\right)\left(x_j-x_{j-1}\right)f^{″}\left(x\right)}-\frac{\text{1}}{\text{2}}\left(f^{\prime }\left(x_0\right){{\varphi }^{″}}_0\left(x\right)+f^{\prime }\left(x_n\right){{\varphi }^{″}}_n(\; x\; )\right)\end{array}$

此时，

${{\varphi }^{″}}_j\left(x\right)=\frac{c^2}{{\left[c^2+{\left(x-x_j\right)}^2\right]}^{\frac{3}{2}}}\ge 0-\text{1}\le {{\varphi }^{\prime }}_{j+1}\left(x\right)\le {{\varphi }^{\prime }}_j\left(x\right)\le 1$

因此，如果 $\left[D_{\text{2}}\left(x_n\right){{\varphi }^{″}}_n\left(x\right)-D_1\left(x_0\right){\varphi }^{″}\left(x\right)\right]\ge \text{0}$，则有 $L_2{f}^{″}\left(x\right)\ge 0$。从而证明拟插值算子 $L_{2}f\left(x\right)$ 具有二阶的保形性，完成证明。

最后，我们将证明算子 $L_{2}f\left(x\right)$ 的收敛性及收敛阶。首先，我们给出两个重要的引理：

引理3.1 [3] 如果 $f\left(x\right)\in C^2\left[a,b\right]$，拟插值算子 $L_{D}f\left(x\right)$ 在 $h\to 0$ 时，满足误差估计

${\Vert f-L_{D}f\Vert }_{\infty }\le K_1{h}^2+K_{2}ch+K_3{c}^2\ln h$ (3.3)

这里， $K_1,K_2$ 和 $K_3$ 为正常数，与 $h$ 和 $c$ 无关。

证明：

拟插值算子 $L_{D}f\left(x\right)$ 可以重新被定义为

$2L_{D}f\left(x\right)={\displaystyle \underset{j=1}{\overset{n-1}{\sum }}{\varphi }_j}\left(t\right)\left(x_{j+1}-x_{j-1}\right){\Delta }^2\left(x_{j-1},x_j,x_{j+1}\right)f+f_0+f_n+\left(x-x_0\right)\left(x_n-x\right){\Delta }^1\left(x_0,x_1\right)f$

在一阶和二阶差分 ${\Delta }^{\text{1}}$ 和 ${\Delta }^{\text{2}}$ 的情况下， $Lf$ 和 $f$ 之间的分段线性插值的差值为

$\text{2}\left(L_{D}f\left(x\right)-Lf\left(x\right)\right)={\displaystyle \underset{j=1}{\overset{n-1}{\sum }}\left({\varphi }_j\left(x\right)-\left|x-x_j\right|\right)}\left(x_{j+1}-x_{j-1}\right){\Delta }^2\left(x_{j-1},x_j,x_{j+1}\right)f$ (3.4)

我们可以得到该函数的界

$\begin{array}{c}\phi \left(x\right)={\displaystyle \underset{j=1}{\overset{n-1}{\sum }}\left({\varphi }_j\left(x\right)-\left|x-x_j\right|\right)}\left(x_{j+1}-x_{j-1}\right)\\ ={\displaystyle \underset{j=1}{\overset{n-1}{\sum }}\left({\left(c^2+{\left|x-x_j\right|}^2\right)}^{\frac{1}{2}}-\left|x-x_j\right|\right)}\left(x_{j+1}-x_{j-1}\right)\ge 0.\end{array}$

分裂一部分带有 $\left|x-x_j\right|\le h$ 以及其余的一部分，这两个部分的估计

${\left(c^2+y^2\right)}^{\frac{1}{2}}-\left|y\right|\le c,c\ge 0,y\ge 0$

${\left(c^2+y^2\right)}^{\frac{1}{2}}-\left|y\right|\le \frac{c^2}{2\left|y\right|},c\ge 0,y\ge 0$

从而得到

$\phi \left(x\right)\le c{\displaystyle \underset{j=1,\left|x-x_j\right|\le h}{\overset{n-1}{\sum }}\left(x_{j+1}-x_{j-1}\right)}+\frac{c^2}{2}{\displaystyle \underset{j=1,\left|x-x_j\right|>h}{\overset{n-1}{\sum }}\frac{x_{j+1}-x_{j-1}}{\left|x-x_j\right|}}\le \text{8}ch+c^2({\displaystyle {\int }_{\left|x-t\right|\ge h}\frac{1}{\left|x-t\right|}\text{d}t+O(\; h\; ))}$

因此我们有

$\phi \left(x\right)\le 8ch+O\left(c^2\ln h\right)+O\left(c^{2}h\right)$

根据(3.4)和 $Lf$ 的 $O\left(h^2\right)$ 收敛阶，当 $h\to 0$ 时， $c$ 趋于零时，它满足下面的约束 $\phi \left(x\right)$。对于 $\left|y\right|\le y^0$， $y^0>0$ 时，我们得到

${\left(1+y\right)}^{\frac{1}{2}}-1\ge \frac{y}{2}-\frac{y^2}{4}$

保持 $\phi \left(x\right)$ 以及 $\left|x-x_j\right|\ge c{y}_0{}^{-1}$ 不变，则有

$\begin{array}{c}\phi \left(x\right)\ge \frac{1}{2}{\displaystyle \underset{j=1}{\overset{n-1}{\sum }}\left(x_{j+1}-x_{j-1}\right)}\left(\frac{c^2}{\left|x-x_j\right|}-\frac{1}{2}\frac{c^4}{{\left|x-x_j\right|}^3}\right)\\ =\left(1+O\left(h\right)\right)c^2{\displaystyle {\int }_{\left|x-t\right|\ge c{y}_0{}^{-1}}\frac{1}{\left|x-t\right|}\text{d}t}-\left(1+O\left(h\right)\right)\frac{c^4}{2}{\displaystyle {\int }_{\left|x-t\right|\ge c{y}_0{}^{-1}}\frac{1}{{\left|x-t\right|}^3}\text{d}t}\end{array}$

这是由 $c^2\left|\ln c\right|$ 作为 $c$ 函数。如果 $c\ge c_0\ge 0$，函数 $\phi \left(x\right)$ 将渐近下界

$2{\displaystyle {\int }_a^b\left({\left(c_0^2+{\left(x-t\right)}^2\right)}^{\frac{1}{2}}-\left|x-t\right|\right)\text{d}t}>0$

现在我们完成证明拟插值算子 $L_{D}f\left(x\right)$ 满足误差估计

${\Vert f-L_{D}f\Vert }_{\infty }\le K_1{h}^2+K_{2}ch+K_3{c}^2\ln h$ (3.5)

引理3.2 基于Largange插值的原理，给出近似一阶导数的三点插值型数值微分公式及其误差

$f^{\prime }\left(x_0\right)=\frac{1}{2h}\left[-3f\left(x_0\right)+4f\left(x_1\right)-f\left(x_2\right)\right]+\frac{h^2}{3}{f}^{(3)}\left({\xi }_0\right)$ (3.6)

$f^{\prime }\left(x_n\right)=\frac{1}{2h}\left[f\left(x_{n-2}\right)-4f\left(x_{n-1}\right)+3f\left(x_n\right)\right]+\frac{h^2}{3}{f}^{(3)}\left({\xi }_n\right)$ (3.7)

证明：

设 $f\left(x\right)\in C^{n+1}\left[a,b\right]$， $x_0,x_1,\cdots ,x_n$ 为 $\left[a,b\right]$ 上的点， $L_n\left(x\right)$ 为 $f\left(x\right)$ 以 ${\left\{x_i\right\}}_{i=0}^n$ 为节点的n次插值多项式。作为 $f\left(x\right)$ 的逼近函数，可用 $L_n\left(x\right)$ 的各阶导数近似 $f\left(x\right)$ 的相应阶导数，即

$f^{(k)}\left(x\right)\approx L_n^{(k)}\left(x\right)={\displaystyle \underset{i=0}{\overset{n}{\sum }}{l}_i^{(k)}\left(x\right)f\left(x_i\right)}k=1,2,\cdots ,n$ (3.8)

其误差为

$f^{(k)}\left(x\right)-L_n^{(k)}\left(x\right)=\frac{d^k}{d{x}^k}\left(\frac{f^{(n+1)}\left(\xi \left(x\right)\right)}{\left(n+1\right)!}{\omega }_n\left(x\right)\right)$ (3.9)

当 $x=x_j,k=1$ 时，有

$f^{\prime }\left(x_j\right)\approx {L^{\prime }}_n\left(x_j\right)={\displaystyle \underset{i=0}{\overset{n}{\sum }}{l^{\prime }}_i}\left(x_j\right)f\left(x_i\right)$ (3.10)

且其误差为

$f^{\prime }\left(x_j\right)-{L^{\prime }}_n\left(x_j\right)=\frac{f^{(n+1)}\left(\xi \right)}{\left(n+1\right)!}{\displaystyle \underset{i=0,i\ne j}{\overset{n}{\prod }}\left(x_j-x_i\right)}$ (3.11)

一般称(3.10)式为近似 $f^{\prime }\left(x_j\right)$ 的 $n+1$ 点插值型数值微分公式。

接下来，给出近似一阶导数( $k=1$ )三点插值型数值微分公式及其误差估计。设 $x_0,x_1,x_{\text{2}}$ 为区间上互异的三个点，则以其节点的2次插值多项式为

$L_2\left(x\right)=\frac{\left(x-x_1\right)\left(x-x_2\right)}{\left(x_0-x_1\right)\left(x_0-x_2\right)}f\left(x_0\right)+\frac{\left(x-x_0\right)\left(x-x_2\right)}{\left(x_1-x_0\right)\left(x_1-x_2\right)}f\left(x_1\right)+\frac{\left(x-x_0\right)\left(x-x_1\right)}{\left(x_2-x_0\right)\left(x_2-x_1\right)}f(\; x\; 2\; )$

其导数

${L^{\prime }}_2\left(x\right)=\frac{2x-x_1-x_2}{\left(x_0-x_1\right)\left(x_0-x_2\right)}f\left(x_0\right)+\frac{2x-x_0-x_2}{\left(x_1-x_0\right)\left(x_1-x_2\right)}f\left(x_1\right)+\frac{2x-x_0-x_1}{\left(x_2-x_0\right)\left(x_2-x_1\right)}f(\; x\; 2\; )$

由式(3.11)可得

$f^{\prime }\left(x_j\right)=\frac{2x_j-x_1-x_2}{\left(x_0-x_1\right)\left(x_0-x_2\right)}f\left(x_0\right)+\frac{2x_j-x_0-x_2}{\left(x_1-x_0\right)\left(x_1-x_2\right)}f\left(x_1\right)+\frac{\text{2}{x}_j-x_0-x_1}{\left(x_1-x_0\right)\left(x_1-x_2\right)}+\frac{f^{(3)}\left({\xi }_j\right)}{3!}\underset{i=0,i\ne j}{\overset{2}{\prod }}\left(x_j-x_i\right)$

令 $x_1=x_0+h,x_2=x_0+2h$，即

$f^{\prime }\left(x_0\right)=\frac{1}{2h}\left[-3f\left(x_0\right)+4f\left(x_1\right)-f\left(x_2\right)\right]+\frac{h^2}{3}{f}^{(3)}(\; \xi \; 0\; )$

$f^{\prime }\left(x_1\right)=\frac{1}{2h}\left[-f\left(x_0\right)+f\left(x_2\right)\right]-\frac{h^2}{6}{f}^{(3)}(\; \xi \; 1\; )$

$f^{\prime }\left(x_2\right)=\frac{1}{2h}\left[f\left(x_0\right)-4f\left(x_1\right)+3f\left(x_2\right)\right]+\frac{h^2}{3}{f}^{(3)}(\; \xi \; 2\; )$

根据上述三式，即得出三点-端点数值微分公式及其误差估计

$f^{\prime }\left(x_0\right)=\frac{1}{2h}\left[-3f\left(x_0\right)+4f\left(x_1\right)-f\left(x_2\right)\right]+\frac{h^2}{3}{f}^{(3)}(\; \xi \; 0\; )$

$f^{\prime }\left(x_n\right)=\frac{1}{2h}\left[f\left(x_{n-2}\right)-4f\left(x_{n-1}\right)+3f\left(x_n\right)\right]+\frac{h^2}{3}{f}^{(3)}(\; \xi \; n\; )$

定理3.4 对于 $f\in C^2\left[a,b\right]$，拟插值算子 $L_{2}f\left(x\right)$ 满足误差估计

${\Vert f-L_{2}f\left(x\right)\Vert }_{\infty }\le \left(K_1+K_4\right)h^2+K_{2}ch+K_3{c}^2\ln h$ (3.12)

这里， $K_1$， $K_2$， $K_3$ 和 $K_4$ 为正常数，与 $h$ 和 $c$ 无关。

证明：令 $L_{2}f\left(x\right)=L_{D}f\left(x\right)+W_{D}f\left(x\right)$，若 $f\left(x\right)$ 是一个连续的函数，则有

${\Vert f-L_{2}f\left(x\right)\Vert }_{{}_{\infty }}={\Vert f\left(x\right)-\left(L_{D}f\left(x\right)+W_{D}f\left(x\right)\right)\Vert }_{\infty }\le {\Vert f\left(x\right)-L_{D}f\left(x\right)\Vert }_{\infty }+{\Vert f\left(x\right)-W_{D}f\left(x\right)\Vert }_{\infty }$ (3.13)

根据引理3.1，我们得到

${\Vert f-L_{D}f\Vert }_{\infty }\le K_1{h}^2+K_{2}ch+K_3{c}^2\ln h$

且根据引理3.2，则有

${\Vert f-W_{D}f\left(x\right)\Vert }_{\infty }\le \frac{h^{\text{2}}}{3},h\to 0$

最后，结合引理3.1和引理3.2,我们证明了拟插值算子 $L_{2}f\left(x\right)$ 满足误差估计 ${\Vert f-L_{2}f\left(x\right)\Vert }_{\infty }\le \left(K_1+K_4\right)h^2+K_{2}ch+K_3{c}^2\ln h$ 注3.1由拟插值算子 $L_{2}f\left(x\right)$ 的收敛性分析可以看出，当 $c=O\left(h^2\right)$ 时，则 ${\Vert f-L_{2}f\left(x\right)\Vert }_{\infty }=O\left(h^3\right)$。因此，拟插值算子 $L_{2}f\left(x\right)$ 的收敛阶数与形状参数c的值有关。

4. 数值实验

在本节中，以 $f\left(x\right)=x^{\text{3}}$ 为待逼近函数，设 $c=0.01,h=0.1$，观察 $f\left(x\right)$ 与拟插值算子 $L_{2}f\left(x\right)$ 的比较结果，如图1所示。接着，选择不同的 $h$ 和形状参数 $c$，比较拟插值算子 $L_{2}f\left(x\right)$ 与 $L_{D}f\left(x\right)$ [3] 及 $L_{s}f\left(x\right)$ [6] 的逼近效果。结果见表1~3所示。最后，在表4中，我们设 $c=h^2$， $h=0.1,0.2,0.01,0.001,0.0001$，观察算子 $L_{2}f\left(x\right)$ 随 $h$ 的变化率。

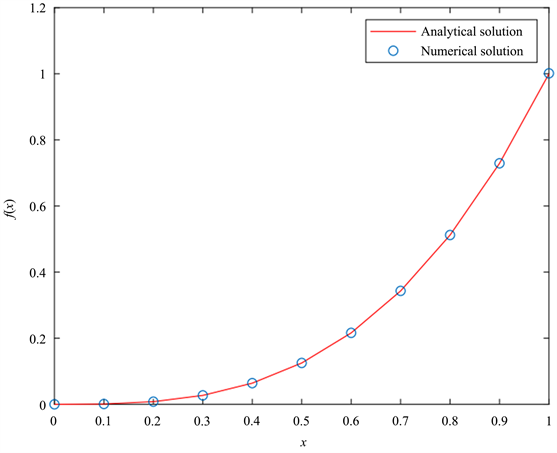
Figure 1. When $c=0.01$, $h=0.1$, the comparison result of the quasi-interpolation operator $L_{2}f\left(x\right)$ and the original function $f(\; x\; )$

图1. 当 $c=0.01$， $h=0.1$ 时，拟插值算子 $L_{2}f\left(x\right)$ 与原函数 $f\left(x\right)$ 的比较结果

Table 1. When $h=0.1$ , c take different values, the quasi-interpolation operator $L_{2}f\left(x\right)$， $L_{D}f\left(x\right)$ and $L_{s}f\left(x\right)$ the error comparison results

表1. 当 $h=0.1$，c取如下不同值时，拟插值算子 $L_{2}f\left(x\right)$， $L_{D}f\left(x\right)$ 及 $L_{s}f\left(x\right)$ 的误差比较结果

Table 2. When $h=0.01$ , c take different values, the quasi-interpolation operator $L_{2}f\left(x\right)$， $L_{D}f\left(x\right)$ and $L_{s}f\left(x\right)$ the error comparison results

表2. 当 $h=0.01$，c取如下不同值时，拟插值算子 $L_{2}f\left(x\right)$， $L_{D}f\left(x\right)$ 及 $L_{s}f\left(x\right)$ 的误差比较结果

Table 3. When $h=0.001$, c take different values, the quasi-interpolation operator $L_{2}f\left(x\right)$， $L_{D}f\left(x\right)$ and $L_{s}f\left(x\right)$ the error comparison results

表3. 当 $h=0.001$ c取如下不同值时，拟插值算子 $L_{2}f\left(x\right)$， $L_{D}f\left(x\right)$ 及 $L_{s}f\left(x\right)$ 的误差比较结果

Table 4. When $c=h^2$, the error comparison result of the quasi-interpolation operator $L_{2}f\left(x\right)$ and the original function $f\left(x\right)$

表4. 当 $c=h^2$ 时，拟插值算子 $L_{2}f\left(x\right)$ 与原函数 $f\left(x\right)$ 的误差比较结果

首先，我们得到了原函数 $f\left(x\right)$ 与拟插值算子 $L_{2}f\left(x\right)$ 的图像。由图1看出拟插值算子 $L_{2}f\left(x\right)$ 曲线与原函数的图像曲线拟合的很好，即拟插值 $L_{2}f\left(x\right)$ 方法与解析解基本一致。拟插值 $L_{2}f\left(x\right)$ 与解析解的误差比较结果如表1所示。

在算例中，我们给出了拟插值 $L_{2}f\left(x\right)$ 在 $h=0.1,c=0.01,0.02,0.05,0.1,0.2$ 时的误差精度比较。由表1可以很容易地发现，随着形状参数c的减小，拟插值 $L_{2}f\left(x\right)$ 的误差也减小。根据表1~3的数值算例，设h分别为 $0.1,0.01,0.001$， $c=0.1h,0.2h,0.5h,h,2h$ 时，分别计算 ${\Vert L_{D}f\left(x\right)-f\left(x\right)\Vert }_{\infty }$ 和 ${\Vert L_{s}f\left(x\right)-f\left(x\right)\Vert }_{\infty }$ 和 ${\Vert L_{2}f\left(x\right)-f\left(x\right)\Vert }_{\infty }$。为了简化，我们假设采样点 ${\left\{x_i\right\}}_{i=0}^n$ 是均匀分布的。通过分析表1~3中的数据，我们发现拟插值算子的逼近能力取决于形状参数c和h，当我们降低参数c和h的值时，我们可以得到更好的逼近效果。从表4，取 $c=h^2,h=0.1,0.2,0.01,0.001,0.0001$，观测算子 $L_{2}f\left(x\right)$ 的收敛速度。很明显,当 $c=O\left(h^2\right)$ 时，拟插值算子 $L_{2}f\left(x\right)$ 的收敛速率可以达到 $O\left(h^3\right)$。此外，我们可以得到在 $c$ 和 $h$ 相同的条件下，拟插值算子 $L_{2}f\left(x\right)$ 的收敛能力优于其他两种。总之，这些数值实验可以说明拟插值 $L_{2}f\left(x\right)$ 是一个性能优良的拟插值算子。

5. 结论

本文通过对Wu-Schaback拟插值格式的改进，构造了一个拟插值算子 $L_{2}f\left(x\right)$，该算子不需要 $f\left(x\right)$ 在端点处的导数，具有很强的实用性。本文详细证明了算子 $L_{2}f\left(x\right)$ 具有良好的保形性、线性多项式的再生性和良好的收敛能力，便于人们在各种应用中使用。在未来，我们计划构造一个拟插值方案，它可以满足更高次多项式的再生性质。另一方面，我们希望将这种构造方法应用到多元空间中，构造一些性质较好的拟插值算子。

基金项目

江西省教育厅科学技术研究项目(GJJ200757)，东华理工大学研究生创新基金(DHYC-202028)。

NOTES

^*通讯作者。