1. 引言
近年来,我国的航天事业发展迅猛,航天器关键技术的地面物理仿真验证也得到越来越多的重视 [1]。基于气浮式模拟器平台开发的地面仿真试验系统已经成为进行航天器地面模拟仿真验证的主要方式。现阶段国内外地面模拟仿真验证系统一般采用的都是较为成熟的三自由度和五自由度模拟器 [2],基本采用气浮球轴承和气足实现三自由度(水平二轴平动加竖直轴转动或三轴转动)和五自由度(三轴转动加水平二轴平动)。传统的五自由度模拟器有局限性,无法做到更加真实的天地一致性,也无法满足越来越复杂的航天器研发和仿真模拟要求。相比于五自由度模拟器,六自由度模拟器增加了竖直方向的零重力实现,这也是技术攻关的难点。竖直方向零重力实现的技术也可转化为月球火星这种低重力环境的模拟。本文所采用的是一种正负刚度恒力弹簧支撑的方法 [3] [4],利用直线电机作为主动力补偿机构,并引入神经网络控制以减小系统恒力输出的误差。
2. 机电复合式恒力弹簧总体设计
机电复合式恒力弹簧的总体结构示意图如图1所示,系统可分为机械式恒力系统和电磁式主动力补偿系统两部分。主要包括刀式凸轮恒力弹簧系统、直线电机、气浮导向装置、称重传感器等。
机械式恒力系统包括刀式凸轮恒力弹簧系统及其支撑件,此部分系统的功能为卸载载荷的绝大部分重力,其结构示意图如图2所示。机械式被动恒力系统在结构上呈左右对称形式,主要组成为一个主弹簧、一对辅助弹簧、一对刀式凸轮及其转轴、滚轮和壳体等部分。竖直弹簧为正刚度弹簧,横向弹簧的力经凸轮传导,并且刀式凸轮表面的曲线使横向弹簧的力在竖直方向的分量与竖直弹簧力的合力为一恒定值。
由于机械式恒力系统当中的机械运动副存在摩擦,且弹簧的刚度、凸轮的加工等均存在一定的误差,机械式恒力系统输出力有一定的波动,这个误差无法满足高精度零重力试验的需求,所以需要有电磁式主动补偿系统对这个输出力误差进行修正。电磁式主动力补偿系统主要由直线电机和力传感器等部分组成。电磁式主动力补偿系统主要用于对机械式恒力系统的输出误差进行补偿,从而提高恒力弹簧整体的恒力输出精度,使竖直方向的零重力模拟更为精确。
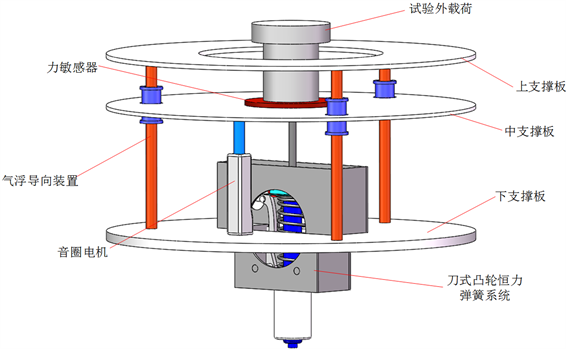
Figure 1. Schematic diagram of electromechanical composite constant force spring
图1. 机电复合式恒力弹簧结构示意图
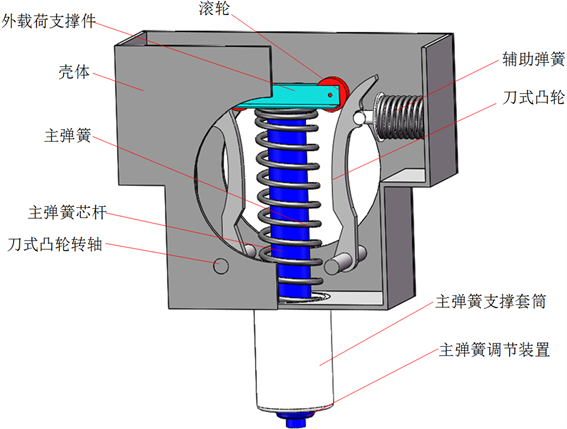
Figure 2. Schematic diagram of mechanical passive constant force system
图2. 机械式被动恒力系统结构示意图
3. 机械式被动恒力系统建模与分析
3.1. 机械式被动恒力系统建模
正如前文所述,对于机械式恒力系统,其力学模型的建立涉及多种复杂的非线性的约束条件,并且加工误差、装配误差都会对恒力系统的输出力精度产生影响,实际产品的力学特性具有很大的不确定性。因此,利用传统数学建模来描述机械式恒力系统的不确定性和内部耦合性具有很大的困难,相比之下,利用神经网络结合试验数据的方法能够很好地建立系统的等价模型。
神经网络开发出了多种形式的模型,其中常用于对非线性系统进行系统辨识的模型共有三类,分别是BP神经网络、基于径向基函数的神经网络 [5] 和模糊神经网络 [6]。这三种网络都属于前置反馈神经网络,具有良好的自学习能力,对被辨识的系统具有很强的逼近能力。本文期望通过三种神经网络对模型的拟合对比,选出一个更加适合的方法。
3.2. 试验设计
在刀式凸轮恒力弹簧系统上方固连一个力传感器,力传感器采集到的数据实时传输给计算机。在力传感器上方放置试验载荷,试验前需调整主弹簧预紧力,使静态时恒力弹簧的力输出值正好等于载荷的重力。试验时采用伺服电动缸对载荷施加外部激励,伺服电动缸能够实现位置和速度的精确控制,进而通过设定速度变化率从而实现加速度的精确控制。
试验所得数据将用作刀式凸轮恒力弹簧的系统辨识,选取载荷在竖直方向上的速度v以及加速度a作为试验参数,通过施加不同的外部激励,获得不同的速度v或加速度a,从而进行多组试验以采集足够多的样本点,同时观察刀式凸轮恒力弹簧的输出力随载荷在竖直方向上的位置的变化情况,具体试验设计情况见表1。

Table 1. Blade cam constant force spring test design table
表1. 刀式凸轮恒力弹簧试验设计表
3.3. 试验结果分析
通过试验可以得到载荷在不同的运动速度和加速度条件下,刀式凸轮恒力弹簧系统的输出力均在载荷重力值附近波动,刀式凸轮恒力弹簧系统输出力可以大致跟随载荷重力。图3为试验过程中采集到的一部分数据。
试验采集的数据共22,688组,记为向量[y, v, a, Fout]形式,其中Fout为输出力。则各采样点的输出力误差为:
(1)
式中
表示第i个数据点的系统力输出误差,
。
Fout的平均值
,标准差
,且输出力误差概率密度近似呈正态分布,根据3
准则,则输出力误差范围为:
(2)
通过以上分析可以得出,恒力弹簧恒力输出误差为
,未能达到预期的误差要求,因此需要使用电磁式主动力补偿系统对机械式被动恒力系统进行输出力补偿,已到达要求的误差范围。
3.4. 系统辨识结果与误差分析
从试验采集的22,688组数据向量[y, v, a, Fout]中,随机选取其中的500组数据作为对照组,对系统辨识结果进行检验,将剩余的22,188组数据分别导入三种神经网络辨识算法中进行机械式被动恒力系统的系统辨识。设置学习次数为50万次,学习均方差目标为
,通过冗余的训练分别观察各辨识算法的收敛、学习速度等情况。对照组数据利用均方差进行辨识精度评估,即:
(3)
三种神经网络算法的辨识结果对比见表2:

Table 2. Comparison table of identification results of three neural network algorithms
表2. 三种神经网络算法的辨识结果对比表
比较上述辨识结果,径向基函数的神经网络由于陷入局部最小点 [7],辨识能力最差,BP神经网络和模糊神经网络能够达到相近的辨识精度,然而模糊神经网络的计算效率明显更高,因此将利用模糊神经网络所辨识的模型作为机械式被动恒力系统的等价模型。
模糊神经网络辨识误差概率密度如图4所示,其误差均值
,标准差
,根据3
准则,其误差范围为[−0.5994, 0.6030]。由对照组实际输出力均值
,可得辨识误差为
,远远小于系统输出力误差,因此所得模型较为准确。

Figure 4. Fuzzy neural network system identification error probability density map
图4. 模糊神经网络系统辨识误差概率密度图
4. 机电复合式恒力弹簧仿真与分析
4.1. 控制系统设计
PID由于其参数较少,较易整定且便于学习与操作,在工业控制领域应用非常广泛,但是PID算法在误差变化快速、非线性等系统当中难以适应,且PID控制也无法满足高精度控制的要求。所以,直线电机的控制系统可基于模型参考神经网络控制系统思想进行设计。模型参考神经网络控制方法(Neural Network Model Reference Adaptive Control, NNMRAC)由国外学者提出,是一种将神经网络控制与模型参考自适应控制相结合的一种新的控制方法 [8]。
4.2. 机电复合式恒力弹簧仿真设计
4.2.1
. 参考模型设计
所设计的控制系统的控制对象是直线电机,对其建立参考模型,此模型即为理想模型。已知直线电机的传递函数为:
(4)
由于仿真是在离散时域中进行,因此将上式转换为离散时域形式:
(5)
式中,i——电流(A);
——时间步长(s);
u——电枢端电压(V);
n——迭代次数。
式(5)中的Fe为模型输出量,ue为模型输入量,右边的直线电机动子与定子相对运动速度ve和电流i为可看做为系统状态量,只有ue作为控制信号,定义该参考模型为模型PE。实际使用中,在参考模型已知的情况下,输入量是由输出量决定的,故还需给出PE的逆模型
:
(6)
可以看出其输入量为Fe,输出量的ue。PE和
的示意图如图5所示。
对于电枢端电压ue还应考虑电压限幅问题,所选用直线电机额定电压为72 V,故设定ue限幅为:
(7)

Figure 5. Reference model and its inverse model
图5. 参考模型及其逆模型示意图
4.2.2
. 神经网络控制器和辨识器设计
神经网络控制器和辨识器的神经网络均选用BP神经网络,此神经网络是离线式的,即每个迭代周期都会新增一组样本,每迭代一次就将最新收集到的样本与之前存储的样本一起放入网络进行新一轮的学习,这种学习方式也称为增量式学习。
此外,对于神经网络控制器,其输出误差不再是神经网络输出与期望值之差,神经网络的输出是控制对象的输入量,用于神经网络学习的输出误差是控制对象的输出量与期望值之差。
4.2.3
. 控制对象模型设计
控制对象的模型为直线电机的实际模型,其形式与参考模型相似。为达到通过计算机仿真验证控制算法的目的,可在参考模型的基础上设置一定的干扰项,模拟控制对象的数学模型。常见的偏差项主要是电机的电阻R、电感L和力常数Ke。取控制对象模型的硬件参数为:
(8)
其中
、
、
分别为被控对象的电阻、电感和力常数;K1、K2、K3为偏置系数。此外,电子系统中的信号必定存在噪声,建模中还需考虑电枢端电压的噪声,一般信噪比不低于70 dB,在仿真过程中利用加性高斯白噪声模拟um的噪声得到
,加入干扰后的被控对象模型为:
(9)
式中,Fm——控制对象模型输出量(N);
——控制对象模型输入量(V)。
同样需对控制对象的电枢端电压u’m做类似式(7)的限幅。
4.2.4
. 系统总体模型设计
机电复合式恒力系统仿真的总体模型如图6所示,其中n是迭代次数,定义试验载荷的竖直位置s、速度v、加速度a以及音圈电机绕组中的电流i为状态量。仿真在离散时域中进行,迭代步长为0.01 s。
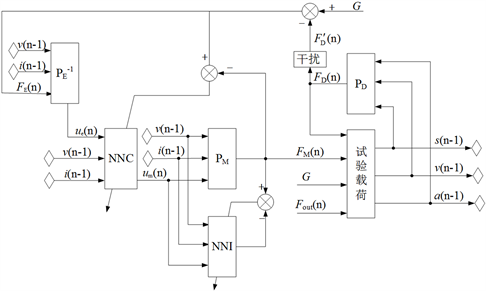
Figure 6. Electromechanical hybrid constant force system overall simulation model
图6. 机电复合式恒力系统总体仿真模型
4.3. 仿真结果分析
4.3.1
. 被控对象模型与参考模型差异的影响
通过修改被控对象模型的硬件参数,考察被控对象硬件参数偏差对恒力输出的影响。试验组号以及每组所对应的被控对象硬件参数偏差系数和恒力输出误差见表3,外作用力
,仿真时间为0~30 s。

Table 3. Controlled object model hardware parameter impact test group table
表3. 被控对象模型硬件参数影响试验分组表
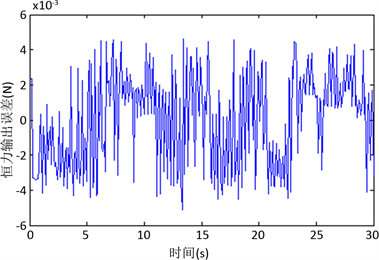
Figure 7. Constant force output after adding armature terminal voltage noise
图7. 加入电枢端电压噪声后的恒力输出情况
选取试验组1-2,在其上添加信噪比为70 dB的电枢端电压噪声进行试验,记为试验组2-1,恒力输出误差如图7所示,加入电压噪声后恒力系统的力输出误差为0.0036%,仍远小于精度指标。
由上述试验结果可知,利用参考模型神经网络控制系统进行恒力系统的控制时,对于参考模型建模精度的要求并不高,神经网络控制器起了一个自适应增益环节的作用,能在控制初期就很好得对建模误差进行补偿。因此被控对象模型和参考模型之间的差异对恒力输出的影响较小。
4.3.2
. 试验载荷运动状态的影响
在试验组2-1的基础上,通过改变外作用力Fout得到试验组见表4,仿真时间为0~30 s,从而验证试验载荷运动状态对系统恒力输出的影响。

Table 4. Test load movement state influence test group table
表4. 试验载荷运动状态影响试验分组表
将试验载荷上施加的外作用力,与试验结果对应观察可发现,恒力系统的动态性越强,输出误差越大。这是由于在力反馈器采样频率一定的情况下,当实验对象运动的动态性越强时,被动恒力系统力输出的阶跃性越强,对控制器的响应能力提出了更高的要求。尽管恒力输出误差随试验载荷运动的动态性增大而增大,但误差量级仍在10−5,远小于0.5%的精度指标要求。
5. 结束语
本文针对竖直方向的零重力模拟的需求,对机电复合式恒力系统进行了设计以及验证,主要研究成果如下:
1) 对机械式被动恒力系统以及电磁式主动力补偿系统进行了设计,并且对其误差的主要来源进行了分析。
2) 对所设计的机械式被动恒力系统建立等价数学模型,基于试验数据利用神经网络对机械式被动恒力系统进行了辨识,并与对照组数据进行比较,验证了等价模型的正确性,且在该模型的基础上施加主动控制并进行仿真和分析。
3) 选择模型参考神经网络控制系统,通过对控制系统进行建模和仿真,分别评估了被控对象模型与参考模型之间的差异以及试验载荷运动状态对控制的影响。试验结果表明,模型差异对恒力输出影响很小,试验载荷运动的动态性越高,系统恒力输出的误差率也越高,但总体量级仍然较小,满足0.5%的预定误差指标,且比1.42%的机械式恒力系统误差要小的多,系统设计及控制效果得到了验证。
基金项目
本文来源于北京卫星环境工程研究所CAST-BISEE项目(项目编号CAST-BISEE2019-014)。