1. 引言
纤维增强材料由于其本身具有强度高、质量轻的优点,现如今被广泛用于各种器件和结构中。Belfield等 [1] 研究了纤维增强弹性板,研究过程中引入了连续自增强思想,同时发展了边界层理论。Verma [2] 研究了弹性自增强体中磁弹性剪切波,并建立了自增强弹性体中电磁场耦合作用中力的基本方程。Chattopadhyay等 [3] 研究了磁弹性剪切波在无限大平面自增强板中的传播问题。Sengupta等 [4] 研究了波在各向异性纤维增强材料表面的传播问题,进而推导出了面波传播理论。Sethi等 [5] 研究了重力作用下各向异性弹性纤维增强材料的波传播问题,得到了不同情况下的波速方程。
在旋转作用下,Othman [6] 研究了广义热弹性平面波模型,同时得到了热应力、位移分量、温度的精确表达式。Othman等 [7] 研究了在磁场和热冲击作用下,弹性介质受旋转作用时各物理量的影响,并将结果与无旋转作用时的预测结果进行了对比。Kumar等 [8] 基于不同热弹性理论下,研究了旋转对有限宽度热弹性板中波传播的影响。Ailawalia等 [9] 研究了旋转效应对弹性体变形的影响,并且利用拉普拉斯变换获得了结构内的温度、应力和位移的分布。Alshaikh等 [10] 研究了广义热弹性压电材料在旋转作用下的平面波速度。
近年来,部分学者们投入了大量的精力来研究固体的裂纹问题,并取得了成就,这在工业电子元件的制造过程中,避免裂纹产生和扩展十分重要。在时间极短的情况下,对于动态裂纹的研究,应当应用广义热弹性理论。Sur等 [11] 利用G-N广义热弹性理论,研究了热弹性功能梯度材料被有限线性I型裂纹削弱,然后产生的位移和应力等问题。Abbas和Prasad等 [12] [13] 应用G-N广义热弹性理论,进而研究了各向同性热弹性模型中的I型裂纹问题。
本文应用Ezzat型分数阶广义热弹性耦合理论,深入研究了半无限大空间二维纤维增强弹性体受线性I型裂纹作用下的热弹性问题,文中运用正则模态法求解,得到了不同参数下无量纲应力、位移和温度的分布,并将各物理量的分布绘出图形,通过对图像的分析,得到了各物理量随着角速度、分数阶参数变化的动态响应,本文为纤维增强材料在力学方面的相关研究提供了新的应用理论。
2. 基本方程
Belfed等提出了纤维增强各向异性弹性介质的本构方程:
(1)
式中,
为应力分量;
为应变分量;
为弹性常数;a为纤维方向,同时
;
为热膨胀系数;
为增强参数;本文选用的纤维方向
。
应变位移关系
(2)
对于二维问题,位移矢量分量可假设为
,同时假设解与坐标z无关。由方程(1)得到:
(3)
(4)
(5)
(6)
其中,
。
分数阶广义热弹性理论下的热传导方程
(7)
其中,
为材料密度;
为热松弛时间参数;
为导热张量;Ce为恒应变比热;T为参考温度;
为温度增量;
为分数阶参数。
3. 热弹性问题描述
该模型受到旋转作用,其中角速度为
,
为沿旋转轴方向的单位矢量,因此上述运动方程含有附加项:并且向心加速度
,Corioli加速度为
。式中
表示动态位移矢量。
基于广义热弹性耦合理论,旋转模型的运动方程:
(8)
将方程(3)~(6)代入(8)式得
(9)
(10)
其中,
。
使用以下无量纲变量
(11)
其中,
。
依据上式,对控制方程进行了无量纲化,同时为了方便省略“
”,得到如下方程:
(12)
(13)
(14)
其中,
。
(15)
(16)
(17)
(18)
4. 正则模态分析
正则模态分析能够给出介质中各物理量的精确解,并且给出的解不受位移、温度、应力分布的假设限制的影响。正则模态分析实际上是在傅里叶变换域内寻找解,并假设所有的场量在变化过程中足够平滑,那么这样函数的正则模态分析就一定存在。文中所考虑物理变量的解可表示为正则模态:
(19)
其中,a是y方向上的波数,
是时间常数,
,
为场量的振幅。
将(19)式代入(12)~(14)式得:
(20)
(21)
(22)
其中
消去(20)~(22)式中
和
中的任意两个,得到
(23)
其中
方程(23)的特征方程如下:
(24)
上述特征方程的根为
。对于边界条件
时,方程(23)式的解给出如下:
(25)
其中
的数值依赖于a和
。联立方程(26)和方程(20)~(21)得
(26)
其中
(27)
因此温度和位移的解可表示为:
(28)
将(28)式代入(15)~(18)式,因此整理可得应力的表达式如下:
(29)
(30)
(31)
(32)
5. 边界条件
应用
表面的边界条件,求取参数
。
应力边界条件:
图1中,假定在
的表面随时间变化,大小为p的周期力,只产生正应力,则
(33)
温度边界条件:
同样,在
表面假设为恒温状态,并且温度大小为f,同时
对z的一阶偏导数为零,则有
(34)
将应力
、温度
的表达式与边界条件(33)、(34)式联立,可得
(35)
其中
。
因此可得到温度、应力和位移的表达式。
6. 数值结果及讨论
利用上述理论,参考论文 [14] 给出具体计算实例,得到计算结果。计算中取以下物理常数:
取计算时间
,得出了不同分数阶参数下,无量纲温度、应力和位移的分布。选取分数阶参数值为
,
和
,同时计算不同角速度
和不同
时,得到了对应无量纲位移、应力和温度的无量纲分布,如图2~19所示。
图2~7给出了
,并且考虑三个不同的
值计算得到无量纲位移、温度和应力在x轴上的分布。
图8~13给出了
时,根据三个不同的
值,得到无量纲位移、温度和应力在x轴上的分布。图14~19给出了
时,考虑三个不同的
值,无量纲应力、位移和温度在x轴上的变化。

Figure 2. Distribution of dimensionless displacement u on x axis when
takes different values
图2.
取不同值,无量纲位移u在x轴上的分布
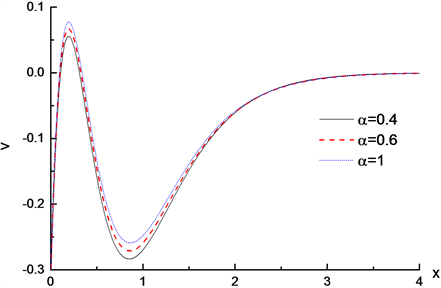
Figure 3. Distribution of dimensionless displacement v on x axis when
takes different values
图3.
取不同值,无量纲位移v在x轴上的分布

Figure 4. Distribution of dimensionless temperature
on x axis when
takes different values
图4.
取不同值,无量纲温度
在x轴上的分布
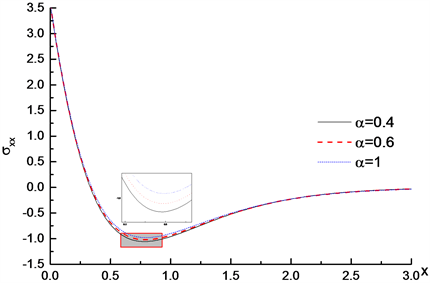
Figure 5. Distribution of dimensionless stress
on x axis with different values of
图5.
取不同值,无量纲应力
在x轴上的分布
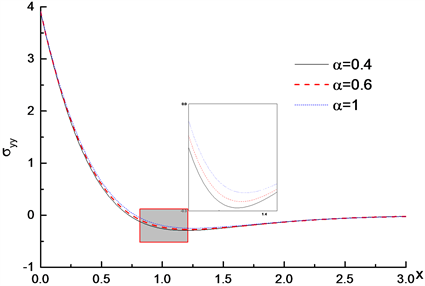
Figure 6. Distribution of dimensionless stress
on x axis with different values of
图6.
取不同值,无量纲应力
在x轴上的分布
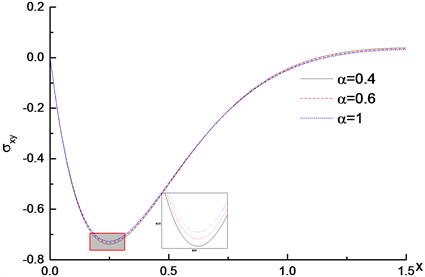
Figure 7. Distribution of dimensionless stress
on x axis with different values of
图7.
取不同值,无量纲应力
在x轴上的分布

Figure 8. Distribution of dimensionless displacement u on x axis when
takes different values
图8.
取不同值,无量纲位移u在x轴上的分布

Figure 9. Distribution of dimensionless displacement v on x axis when
takes different values
图9.
取不同值,无量纲位移v在x轴上的分布
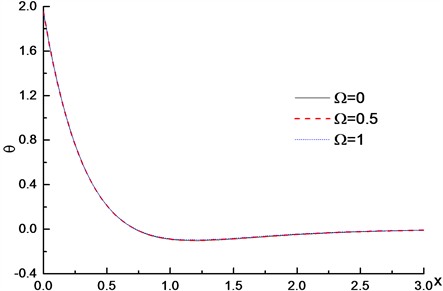
Figure 10. Distribution of dimensionless temperature
on x axis when
takes different values
图10.
取不同值,量纲温度
在x轴上的分布
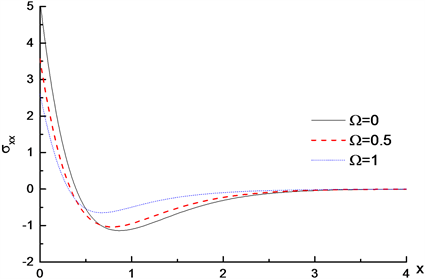
Figure 11. Distribution of dimensionless stress
on x axis with different values of
图11.
取不同值,无量纲应力
在x轴上的分布
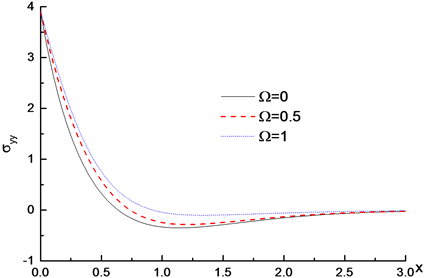
Figure 12. Distribution of dimensionless stress
on x axis with different values of
图12.
取不同值,无量纲应力
在x轴上的分布

Figure 13. Distribution of dimensionless stress
on x axis with different values of
图13.
取不同值,无量纲应力
在x轴上的分布

Figure 14. Distribution of dimensionless displacement u on x axis when y takes different values
图14. y取不同值,无量纲位移u在x轴上的分布

Figure 15. Distribution of dimensionless displacement v on x axis when y takes different values
图15. y取不同值,无量纲位移v在x轴上的分布

Figure 16. Distribution of dimensionless temperature
on x axis when y takes different values
图16. y取不同值,无量纲温度
在x轴上的分布

Figure 17. Distribution of dimensionless stress
on x axis with different values of y
图17. y取不同值,无量纲应力
在x轴上的分布

Figure 18. Distribution of dimensionless stress
on x axis with different values of y
图18. y取不同值,无量纲应力
在x轴上的分布
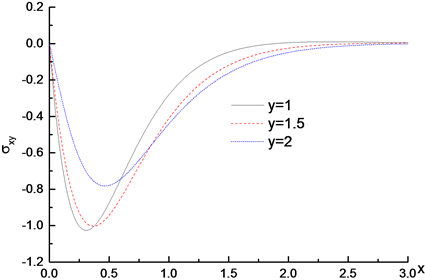
Figure 19. Distribution of dimensionless stress
on x axis with different values of y
图19. y取不同值,无量纲应力
在x轴上的分布
图2所示,分数阶参数取不同值,无量纲位移u沿x轴的分布。可知位移u在边界上有最大值,说明在裂纹开始处的位移u最大,然后随着x值增加逐渐减小,最终收敛于零。由局部放大图可知,同一位置处,分数阶参数的值越小,预测得到的位移u的数值也越小,说明不同分数阶参数的值对位移u的预测结果不同。图3显示无量纲位移v在x轴上的分布,由图观察可知位移v在边界处取得最小值,在x轴上呈波动趋势,最终收敛于零。分数阶参数值越大,预测的位移v的值越小。正是由于各向异性纤维增强材料在两个方向上的材料特性不同,可知该纤维增强材料更倾向于抵抗垂直位移,因此该材料在两个方向上的位移分布表现不同。
图4显示分数阶参数不同,无量纲温度
在x轴上的分布情况。可知温度
在边界上取得最大值,随着x值的增加逐渐减小,最终收敛于零,这是由于边界处距离热源最近,随着x远离热源,温度逐渐减小。并且在x取相同值,分数阶参数越大时预测的温度值越高。图5显示分数阶参数不同,无量纲应力
沿x轴的分布。由图可知,在边界处应力
取得最大值,随着远离边界应力
逐渐减小,在
处,达到最小值,然后逐渐增加,最后收敛于零;在相同位置处,分数阶参数值越大预测的应力
值也越大。
图6显示不同分数阶参数下,无量纲应力
沿x轴的分布,由图能够看出应力
在边界处取得最大值,然后随着x远离边界而逐渐减小,在
处达到最小值,随后逐渐增加,最终收敛于零。在
附近,分数阶参数值越大,所预测的应力
值越小。将应力
与应力
的分布对比,可知由于在两个方向上的材料特性不同,造成应力在两个方向上的分布不同。图7显示分数阶参数不同,无量纲应力
的分布,可知应力
在边界处取值为零,由于该模型在边界上无切应力,因此满足边界条件,然后随着x远离边界,应力
取值逐渐减小,在
位置,应力
达到最小值,然后逐渐增大,最终收敛于零,并且分数阶参数的值越大,预测的应力
值越大。应力
的分布趋势,满足各向异性材料的热弹性性质,也满足该模型的边界条件,因此分布情况是合理的。
图2~7表明分数阶参数的不同,对物理量的预测结果不同,即物理量的分布不同。各物理量在x轴上的分布变化,都满足材料特性和边界条件。
图8显示
取不同值,无量纲位移u沿x轴的分布,位移u始终为正值,并且随着x远离边界逐渐减小,最终收敛于零。在远离边界位置,
值越大预测的位移u的结果越小,这表明旋转效应减小位移u的值。图9显示
值越大预测的无量纲位移v越小,但是
取不同值,位移v的分布趋势不变,并且最终都收敛于零,因此旋转角速度的增加,减小位移v的幅值。通过其与图8对比,由于各向异性材料在两个方向上的材料参数不同,因此引起的位移分布不同。图10显示
取不同值,无量纲温度
的分布无改变,因此旋转效应不影响介质中的温度分布,即温度的分布不受旋转效应的影响。
图11显示
取不同值,无量纲应力
的分布。由图可知,
不改变应力
的走势,在
处,应力取得最小值,并且
值越大,应力
绝对值越小,旋转效应的存在,减小应力
的幅值。图12显示
取不同值,无量纲应力
都在边界位置取得最大值,随着x远离边界,逐渐减小最后收敛于零。在x取值相同时,
值越大,预测应力
值也越大。图13显示
取不同值,无量纲应力
沿x轴的分布,由图可知,在边界位置应力
为零,之后递减达到最小值后逐渐增加,最终收敛于零,
取不同值,不改变应力
的走势,只影响其最小值。随着旋转角速度的增加,应力
的振幅减小,说明旋转效应对应力
有显著影响。
图8~13表明旋转效应的存在减小应力、位移的振幅,不影响温度的分布,即温度分布不受弹性体旋转的影响,而应力、位移的分布受旋转效应的影响显著。同时,由于两个方向上的材料特性不同,旋转对两个方向上应力、位移的影响也有差别。
图14显示y取不同值,无量纲位移u沿x轴的分布。由图可知,x取相同值,随着y值增加,位移u减小,说明外载荷在距离较远位置对位移产生的影响变小。y取值不同,不改变位移u的分布趋势,随着x远离边界,位移u最终收敛于零。图15显示y取不同值时,无量纲位移v呈先增大后减小的分布趋势,最终收敛于零。在远离边界的位置,y值越大位移v越大,这是由于材料在两个方向上的材料参数不同导致的。图16显示y取不同值,无量纲温度
在x轴上的分布,由图可知,在边界处温度达到最大值,然后减小,最终趋向于零。这是由于在边界处距离热源最近,产生的温度最大。在x取相同位置,y越大的位置,预测的温度
值越大。图17显示y取不同值,无量纲应力
沿x轴分布情况。应力
在边界位置有最大值,远离边界逐渐减小最终收敛于零。y取不同值,只影响其大小,不影响其分布走势。在x轴相同位置,y取值越小,相应的应力
越小。图18显示无量纲应力
沿x轴分布,图形分布趋势与应力
相似,都是在边界位置取得最大值,之后逐渐减小,最终都收敛于零。在x轴相同位置,y值越大,对应应力
值越小。图19显示无量纲应力
沿x轴分布趋势。由图可知,在边界位置应力
为零,之后逐渐减小,在
位置达到最小值,同时y值越小,得到的最小值也越小,最后逐渐增加并收敛于零。应力
的分布趋势符合应力
边界上为零的边界条件,也符合纤维增强材料中切应力的分布规律。
图14~19表明半无限大纤维增强弹性体的位置不同,各物理量的分布不同,由于外载荷引起的动态响应在传播过程中的不同,弹性体中各物理量的分布与弹性的空间位置有关。
取
,在x轴固定位置(
和
),给出无量纲位移u、v和应力
随时间t的变化情况,如图20~22所示。

Figure 20. When x takes different values, the dimensionless displacement u changes with time t
图20. x取不同值,无量纲位移u随时间t的变化

Figure 21. When x takes different values, the dimensionless displacement v changes with time t
图21. x取不同值,无量纲位移v随时间t的变化

Figure 22. The change of dimensionless stress
with time t when x is different
图22. x取不同值,无量纲应力
随时间t的变化
如图20所示,在x轴上固定位置,无量纲位移u随时间的变化,从零开始,随时间增加逐渐减小。图21所示,在x轴上固定位置处,无量纲垂直位移v最初为零,随时间t的增加逐渐增大。这是由于在研究的弹性介质中,弹性体在两个方向上的材料特性不同导致的。因此纤维增强弹性体在两个方向上位移表现出不同力学行为。在x轴不同位置,位移随时间变化不同,距离热源越远位置,热膨胀变形时间越晚,相应位移绝对值越小,反映出热波在弹性体中传播速度有限。图22显示x轴固定位置处,无量纲应力
随时间的变化。结果表明距离热源较近位置,应力
随时间变化梯度较大,但是具有相同变化趋势。
由于时间不同,各物理量的分布不同,因此能够得出弹性体中波的传播速度是有限的,同时各物理量的分布与时间有关。
7. 结论
本章基于分数阶广义热弹性理论,得到正则模态分析法的解析解,使正则模态法的应用得到发展,同时得到各物理量在距离裂纹边缘不同距离的分布情况。本章研究了不同参数,如分数阶参数、旋转效应,对各物理量的影响,并将研究结果与论文 [14] 结果进行了相关比较。结果表明:
1) 分数阶参数的不同导致预测的结果不同,因此不同分数阶参数下,对弹性体内物理量的分布预测结果不同。例如,不同分数阶参数下,位移v、温度、应力的分布不同;
2) 由于转速影响物理量的振幅,大多数物理量随着转速的增加,振幅减小。因此可得旋转效应的存在该模型中具有重要意义;
3) 不同分数阶参数下,无量纲位移、温度、应力的大小、分布不同,在相同分数阶参数下,各物理量的分布随着坐标值得增加而变化。因此,各物理量的大小及分布,不仅取决于分数阶参数,还受时间和空间变量的影响;
4) 各物理量的大小随着距离远离边界都趋向于零,表明在半无限大弹性体中,外力冲击仅在一定范围内形成影响,并不能无限传播,这与材料中物理量传播的事实是一致的,同时所有表示物理量的函数都是连续的,表明各物理量在传播过程中不会产生突变,这也符合纤维增强材料的材料特性。