1. 引言
航天发射测控主要完成航天器发射主动段的跟踪测量、航天器定初轨,为确保航天器安全快速入轨提供及时有效的支持 [1]。测控链路是地面站与卫星进行“对话”过程中建立的通信链路,能够按照规定的消息格式和通信协议实时传输处理格式化数字信息 [2]。在发射任务前均需要完成测控链路分析,为地面站制定跟踪捕获方案提供参考依据。
在每次发射任务前,需要根据主动段理论弹道和姿态文件开展试验任务跟踪条件分析,包括星站可见性分析、遮蔽角分析、天线测控角分析和测控链路电平估算等工作 [3]。通过对星站可见性和遮蔽角进行分析可以得到卫星对地面站的可见情况。天线测控角分析的结果能够用于研判设备接收到的信号强弱。测控链路电平估算主要用于评价卫星对上行电平变化的敏感程度以及设备接收电平是否满足测控跟踪要求 [4]。
在工业部门提供的主动段理论弹道和姿态文件中,理论弹道文件是火箭在地固系中的位置和速度,理论姿态文件是火箭本体系相对于发射惯性坐标系中的姿态角。在计算天线测控角时,需要将运载火箭到地面站的连线矢量从地固系转换到火箭本体系中。传统计算方案中,通过地心赤道惯性坐标系将地固系和发射惯性坐标系关联起来,但地固系与地心赤道惯性坐标系的转换需要涉及到历元恒星时,也就是说需要输入发射T0时刻;此外,在计算天线测控角
时不够简洁,将卫星天线指向矢量和运载火箭到地面站的连线矢量投影到地固系中进行了夹角解算,但本质上测控角
是一个夹角,无论是在地固系还是在火箭本体系,其大小都是一致的,因此可在火箭本体系中直接计算卫星天线指向和运载火箭到地面站的连线矢量的夹角。
针对上述问题,本文根据任务前提供的地固系中理论弹道文件和发惯系中的理论姿态文件,通过引入发射坐标系,设计了一种无需输入火箭发射T0时刻的卫星天线测控角和测控链路余量计算方案,与传统计算方案相比,计算效率更高。
2. 坐标系定义及转换关系
2.1. 坐标系定义
1) 地心固连坐标系(e系)
坐标系原点
与地心重合,基准平面
与地球赤道面重合;
轴指向赤道平面与格林尼治子午线的交点方向;
轴与地轴重合,指向北极;
轴与
轴、
轴一起构成右手坐标系。
2) 发射坐标系(F系)
坐标系原点
位于发射工位,
平面为经过坐标原点与地球参考椭球面相切的切平面;
轴位于该切平面指向发射方向,通常由发射方位角A定义,A为发射方向与当地正北的夹角,顺时针度量为正;
轴为切平面通过发射工位原点的法向,向上为正;
在切平面内与
轴正交。发射坐标系与地球固连,是动坐标系。
3) 发射惯性坐标系(A系)
发射惯性坐标系为惯性不动系,该坐标系与发射瞬间的发射坐标系重合,而后在惯性空间定位、定向。
4) 火箭本体坐标系(b系)
坐标系原点位于火箭质心
,
轴为箭体纵对称轴指向头部尖端;
轴在箭体纵平面内与
轴垂直且指向上方;
轴为箭体纵对称面法向,与
,
轴成右手坐标系。因此,称
轴为滚动轴,
轴为偏航轴,
轴为俯仰轴,如图1所示 [5]。

Figure 1. The relationship between the rocket body and the launch coordinate system
图1. 火箭本体坐标系与发射坐标系关系图
5) 卫星本体坐标系(s系)
通常,坐标系原点位于卫星质心
,
轴为卫星纵对称轴,指向卫星头部为正;
轴位于卫星纵对称面内,与
轴垂直,指地为正;
轴为卫星纵对称面法向,与
,
轴成右手坐标系。
一般来说,卫星天线都是±Z轴正装或斜装,此时可定义卫星天线安装俯仰角
和安装方位角
两个角度描述卫星天线在卫星本体系中的单位矢量:
卫星天线安装示意图如图2所示,天线安装角正负号定义如下:
1)卫星天线安装俯仰角
:天线方向与卫星本体系XOY平面上的夹角,指向+Z方向为正,若卫星天线为+Z轴安装,则此值为90度。
2)卫星天线安装方位角
:天线方向在卫星本体系XOY平面上的投影与X轴的夹角,从卫星本体+Z轴方向向原点看去逆时针方向旋转为正,若卫星天线为+Z轴安装,则此值为0度。

Figure 2. Schematic diagram of satellite antenna installation in the satellite body coordinate system
图2. 卫星天线在卫星本体坐标系安装示意图
2.2. 坐标转换关系
2.2.1. 地固系到发射坐标系转换
假设发射工位大地经度为
,纬度为
,发射方位角为
,发射坐标系示意图如图3所示:

Figure 3. The relationship between the Earth fixed and the launch coordinate system
图3. 地固系与发射坐标系关系图
根据文献 [6] 可知,地固系(e系)到发射坐标系(F系)的转换矩阵
为
(1)
其中:
这里,
,
,
为初等转换矩阵,分别表示绕x轴,y轴,z轴旋转
角的坐标转换矩阵。
2.2.2. 发射坐标系到发射惯性坐标系转换
根据文献 [6] 可知,发射惯性坐标系(A系)到发射坐标系(F系)的转换矩阵
为
(2)
式中,地球自转角速
,t为相对于发射时刻T0的航时,这在理论姿态文件中会提供,
为反对称矩阵。
其中,
于是,发射坐标系(F系)到发射惯性坐标系(A系)的转换矩阵为
(3)
2.2.3. 发射惯性坐标系到火箭本体系转换
根据理论姿态文件中提供的火箭本体系相对于发射惯性系的俯仰角
,偏航角
,滚动角
,姿态角转序为“321”,可得发射惯性坐标系(A系)到火箭本体系(b系)的转换矩阵
为
(4)
2.2.4. 地固系到火箭本体坐标系转换
综上所述,根据姿态矩阵递推性可得地固系(e系)到火箭本体坐标系(b系)的转换矩阵
为
(5)
3. 天线测控角计算方法
3.1. 天线测控角定义
在每次试验任务前,开展地面站跟踪条件分析,需要对天线测控角进行分析,了解在任务跟踪弧段内,卫星天线角可见情况。在天线增益干涉区,会出现接收信号电平波动、甚至可能失锁的现象。通过对天线测控角的变化情况进行分析,可提前做好地面设备接收信号的跟踪研判。
实际工作中,卫星天线测控角包含
和
。
是指运载火箭到地面站的连线在运载火箭本体系YOZ面上的投影与OY轴的夹角,从+X方向向原点O看去,自OY轴起逆时针为正,其范围为
;
是指卫星天线指向与运载火箭到地面站连线的夹角,其范围为
。若
角在卫星天线波束范围内,则天线角可见;若
角超出卫星天线波束范围,则天线角不可见。
3.2. 天线测控角计算
本节根据任务前提供的地固系中理论弹道文件和发惯系中的理论姿态文件,设计一种无需输入火箭发射T0时刻的天线角计算方案。
地面站站址在地固系中的坐标
为
(6)
式中,e为偏心率,h0为地面站大地高,B0为地面站大地纬度,λ0为地面站大地经度,N为站址的卯酉圈曲率半径。
运载火箭到地面站的连线在地固系中位置矢量为
(7)
式中,
为火箭在地固系中的位置矢量。
利用公式(5)中的姿态转换矩阵
,可将地固系中的位置矢量
转换到火箭本体系,即可得运载火箭到地面站的连线在火箭本体坐标系中位置矢量为
(8)
根据3.1节中的天线测控角定义,可求得天线角
为
(9)
式中,
为位置矢量
的三分量。
根据卫星与火箭的安装关系,可求得卫星本体系(s系)到火箭本体系(b系)的转换矩阵
。由转换矩阵
和卫星天线在卫星本体系中的单位矢量
,可进一步求得卫星天线在火箭本体系中的单位矢量:
根据2.1节中的天线角定义,可求得天线角
为
(10)
4. 测控链路电平分析计算
4.1. 卫星接收电平及余量计算
卫星接收电平具体计算公式为
(11)
其中:
1)
为地面天线等效各向同性辐射功率,单位为dBW。
2)
为卫星天线增益,单位为dBi。
3)
为上行路径损耗,计算公式为
。其中:
为卫星上行频率,单位为MHz;R为通信距离,单位为km。
4)
为上行其他损耗,单位为dB,包括极化损耗、大气吸收损耗、天线指向误差损耗和馈线损耗等,根据经验取值。
因此,可以得出卫星接收电平余量为
。其中,
为卫星接收机解调门限,单位dBm,取经验值。
4.2. 地面接收载噪比及余量计算
地面接收载噪比具体计算公式为
(12)
其中:
1)
为卫星天线等效各向同性辐射功率,单位为dBW。
2)
为地面接收G/T值,单位为dB/K。
3)
为下行路径损耗,计算公式为
。其中:
为卫星下行频率,单位为MHz;R为通信距离,单位为km。
4)
为下行其他损耗,单位为dB,包括极化损耗、大气吸收损耗、天线指向误差损耗和馈线损耗等,根据经验取值。
5) K为波尔兹曼常数,取定值−228.6 dB/K。
因此,可以得出地面接收电平余量为
。其中,
为地面接收保精度载噪比(C/N0),单位dBHz,取经验值。
5. 仿真分析
按照本文提出的计算方法,选取某北斗卫星任务,依据理论弹道姿态数据,对某参试设备跟踪卫星天线性能进行仿真分析,分别对卫星天线测控角和测控链路电平进行计算。仿真结果如图4至图8所示,仿真结果与实际跟踪结果相吻合。
5.1. 设备跟踪卫星天线及动态分析
设备跟踪卫星可见弧段及动态仿真结果如图4~6所示。其中,图4为遮蔽可见性分析,图5为距离可见性分析,图6为方位—俯仰角速度动态曲线,图7为方位–俯仰角加速度动态曲线。
根据图4和图5仿真结果可知,设备在任务弧段T0 + 330 s到T0 + 652 s,设备跟踪距离R、距离变化率V满足目标动态变化需求。从图6和图7可以看出,设备方位角最大速度5.8˚/s、俯仰角最大速度1.2˚/s,设备方位角最大加速度0.38˚/s2、俯仰角最大加速度0.17˚/s2,设备指标满足目标动态特性要求,设备可正常跟踪动态目标。
设备跟踪卫星的天线角仿真结果如图8所示。
从图8可以看出,设备从进站点3˚开始(T0 + 289 s)到临界点(T0 + 491 s),β角在26˚~95˚之间变化(跟踪+Z轴天线),卫星天线角可见,卫星+Z轴天线对地张角处于稳定增益区,设备对+Z面天线信号进行稳

Figure 4. The analysis curve of masking visibility
图4. 遮蔽可见性分析图

Figure 5. The analysis curve of distance visibility
图5. 距离可见性分析图

Figure 6. Angular velocity dynamic curve
图6. 角速度动态曲线图
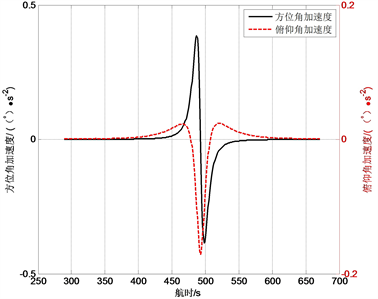
Figure 7. Angular acceleration dynamic curve
图7. 角加速度动态曲线图

Figure 8. Antenna direction angle of the satellite +Z axis
图8. 卫星+Z轴天线方向角β
定跟踪测控;从T0 + 492 s以后由于+Z面天线角超限,卫星+Z轴天线对地张角处于增益下降区,在此弧段内可能出现下行信号起伏,将影响到设备的稳定跟踪。
5.2. 设备跟踪卫星测控链路电平分析
设备跟踪卫星的测控链路电平仿真结果如图9和图10所示。
根据图9仿真结果可知,设备任务跟踪弧段(T0 + 330 s到T0 + 652 s)内,星上上行实际接收信号电平值最小为−80.1 dBm,最大为−67.5 dBm,满足星上灵敏度-112 dBm的要求;上行信号余量最小为30.5 dB,最大为45 dB,满足卫星对上行信道电平的变化要求,设备上行测控链路电平满足跟踪测控要求。
根据图10仿真结果可见,在任务弧段内,设备下行接收信号电平值最小为83.8 dBHz,最大为98.1 dBHz,远远大于地面设备51 dBHz的锁定门限,地面设备可稳定锁定下行信号;下行信号余量最小值为32.8 dB,最小为47.5 dB,下行接收信号电平满足设备跟踪测量要求,可正常完成卫星下行信号接收解调工作。

Figure 9. Satellite receiving level and margin curve
图9. 卫星接收电平及余量图

Figure 10. Ground receiving carrier-to-noise ratio and margin curve
图10. 地面接收载噪比及余量图
6. 结论
本文针对地面站接收机与卫星之间的测控链路提出了一种基于理论弹道与姿态文件的非关联火箭发射T0时刻的实时天线测控角和测控链路余量计算方案,该方法结合不同的研究对象可推导出具体的计算过程,具有广泛的实用性。通过仿真结果分析,本文提出的方法准确有效、符合工程实际,可以为后续任务的开展和工程研制提供技术支持,具有广泛的工程实践前景。